5
Uniform and Preferential Flow Mechanisms in the Vadose Zone
Jan M.H. Hendrickx1 and Markus Flury2
ABSTRACT
The two major flow mechanisms in the vadose zone are uniform flow and preferential flow. Both types of flow occur often simultaneously, but have considerably different consequences for water flow and chemical leaching. The objectives of this paper are to describe and classify flow mechanisms in the subsurface and to present illustrative field and laboratory studies. Since preferential flow occurs at a number of scales, scale is used as the primary classification criterion. Three distinctive scales are recognized on the basis of three different conceptual and physical models for water flow in the vadose zone: pore scale, Darcian scale, and areal scale. A common example of pore-scale preferential flow is saturated and unsaturated flow through macropores and fractures. At the Darcian scale we observe flow through stony soils, unstable flow occurring in water repellent and wettable homogeneous soils, unstable flow in layered soil profiles, preferential flow induced by variability in soil hydraulic properties, and flow through displacement faults. At the areal scale, surface depressions and discontinuous layers with lower or higher permeabilities can cause preferential flow. The paper concludes with a short section on measurement techniques for preferential flow and with guidelines for the formulation of conceptual models for the vadose zone.
|
1 |
Department of Earth and Environmental Science, New Mexico Tech, Socorro |
|
2 |
Department of Crop and Soil Sciences, Washington State University, Pullman |
INTRODUCTION
It has long been recognized that water flow in soils can either be uniform (Green and Ampt, 1911) or non-uniform (Lawes et al., 1881). Uniform flow leads to stable wetting fronts that are parallel to the soil surface; non-uniform flow results in irregular wetting. As a direct consequence of these irregular flow patterns, water moves faster and with increased quantity at certain locations in the vadose zone than at others. This non-uniform movement of water and dissolved solutes is commonly denoted preferential flow.
The term preferential flow neither distinguishes between the causes of the non-uniform flow pattern nor differentiates between the types of patterns. As such the term preferential flow comprises all phenomena where water and solutes move along certain pathways, while bypassing a fraction of the porous matrix. The reasons for the non-uniform flow patterns are manifold, and several identified mechanisms have coined an own term: Macropore flow is preferential water movement along root channels, earthworm burrows, fissures, or cracks. It occurs predominantly in fine-textured soils or media with a pronounced structure. Water bypasses the denser and less-permeable soil matrix by using the pathway of least resistance through macropores. Unstable flow is often observed in coarse-textured materials, and may be induced by textural layering, water repellency, air entrapment, or continuous non-ponding infiltration. As in the case of macropore flow, a considerable portion of the porous matrix is bypassed by the infiltrating water. Funnel flow refers to the lateral redirection and funneling of water caused by textural boundaries. Water again moves along the pathway of least resistance and can be redirected through a series of less permeable layers embedded in the soil profile. Each of these types of preferential flow is caused by different physical mechanisms. Often, several mechanisms act simultaneously, which leads to a broad variety of flow patterns.
The objectives of this paper are to describe the mechanisms and processes that lead to uniform and preferential flow in the vadose zone, and to elucidate the differences in the types of flow patterns observed. The different types of preferential flow are discussed in terms of three different conceptual and physical models for water flow which are frequently used in vadose zone hydrology and lead to the recognition of three spatial scales. We present illustrative examples and provide the basis for conceptual models to describe preferential flow phenomena.
CONCEPTUAL AND PHYSICAL MODELS
The physical principles that govern flow and capillary processes in the vadose zone are well understood and many excellent text books are available that deal with this topic at both introductory (Campbell, 1985; Hanks and Ashcroft, 1986; Hillel, 1998; Jury et al., 1991; Koorevaar et al., 1983; Marshall and Holmes, 1979) and advanced levels (Bear, 1972; Childs, 1969; Corey, 1990; Dullien,
1992; Kirkham and Powers, 1972). Flows of incompressible Newtonian fluids such as water are mathematically described by the Navier-Stokes equations, which are nonlinear, second-order, partial differential equations. These equations are related to a conceptual model for the pore scale that is based on the concept of a fluid continuum filling the void space. This approach is valid if the size of the pore diameters is larger than the mean free path of the water molecules. Although the continuum condition is readily met in most flow conditions in the vadose zone, the intricacy of the Navier-Stokes equations allows only a few exact mathematical solutions (Currie, 1993). One of these is the Hagen-Poiseuille equation that describes laminar flow through circular tubes (flow through a pore), between two parallel plates (i.e., flow through a fracture), and over a plate (i.e., film flow).
For example, the water flux qfr(m/s) through a saturated parallel, smooth-walled fracture with aperture opening b (m) under laminar flow conditions is
(5.1)
(Bear et al., 1993; Corey, 1990; Snow, 1969; Streeter et al., 1998), where H is total hydraulic head (m), z is vertical distance (m), and Kfr is the hydraulic conductivity in the fracture (m/s) defined as:
(5.2)
where ρ is fluid density (kg/m3), g is the acceleration due to gravity (m/s2), and µ is the dynamic viscosity (kg/s · m).
The geometrical complexity of porous materials makes it very cumbersome to treat water flow by referring only to the fluid continuum filling the pore space. A solution for this problem is found by moving to a larger spatial scale, which we name in this paper the Darcian scale. Instead of trying to exactly describe pore geometries and corresponding boundary conditions, the actual multiphase porous medium is replaced by a fictitious representative volume consisting of many pores and solids over which an average is performed. This changes the conceptual model from one based on a fluid continuum at the pore scale to one based on the concept of a representative volume at a larger spatial scale.
At the Darcian scale, water movement through a one-dimensional, unsaturated, vertical soil column is mathematically expressed by Darcy-Buckingham's equation:
(5.3)
where q is the water flux (m/s), K(h) the unsaturated hydraulic conductivity (m/s), and H the total hydraulic head:
H = h + z (5.4)
in which h is the (negative) water pressure (m) and z the elevation head or height above a reference level (m).
Equations 5.1 and 5.3 have the same functional form; that is, the flux is proportional to the total hydraulic gradient. However, the proportionality factors in the two flux laws are fundamentally different. The hydraulic conductivity in the fracture Kfr applies to a single aperture whereas the hydraulic conductivity K(h) is defined over a representative volume of the porous medium. As a result K(h) is much more complex than Kfr, which is, for a given fluid, completely defined by a single soil or rock parameter: the aperture width (see Equation 5.2).
Only empirical formulations of the hydraulic conductivity K(h) exist. Several mathematical functions have been proposed to represent measured data. The complexity of the unsaturated hydraulic conductivity is apparent in the function proposed by Van Genuchten (1980):

(5.5)
where Ks is the saturated hydraulic conductivity (m/s); θ is volumetric soil water content (m3/m3); θs is the saturated water content (m3/m3), often taken equal to the soil porosity; θr is residual water content (m3/m3); and the parameters n, m, and λ are empirical constants. The relationship between θ and h, the water retention characteristic, is:
(5.6)
where α (m−1), n, and m are parameters that determine the water retention curve shape. As it is often assumed that m = 1 − 1/n, the number of parameters needed to describe the hydraulic conductivity as a function of soil water pressure h totals six: Ks, θs, θr, n, λ, and α. The parameter values can be determined from measured θ-h and K-h data pairs using nonlinear curve fitting programs available in statistical software packages and spreadsheets, or by optimization software such as the package RETC developed by Van Genuchten et al. (1991).
At the areal scale, application of the Darcy-Buckingham equation is no longer practical since it would require long and expensive field campaigns to characterize and quantify the spatial variability of the vadose zone at the Darcian scale. One approach for the evaluation of water movement at such a big scale is to employ areal mass balance or soil moisture budgeting models (Hendrickx and Walker, 1997). For example, the groundwater recharge over a large area can be assessed by an areal water balance equation:
qr= P + R − ET − ΔW (5.7)
where qr is the groundwater recharge (m/month), P is precipitation (m/month), R is the net runoff/runon (m/month), ET is actual evapotranspiration (m/month), and ΔW is the change in soil moisture storage in the vadose zone (m/month).
Table 5-1 follows previous work by Wagenet (1998), Wagenet et al. (1994), and Wheatcraft and Cushman (1991) to summarize the principal characteristics of the conceptual and physical models discussed above. One immediate observation of great practical significance is the fact that conceptual models at different scales result in different physical models and mathematical equations. Moreover, each of these equations requires a completely different set of input parameters. The complexity of input parameters for physical models increases with the spatial scale. Flow in a fracture requires a measurement of its width; unsaturated flow through a soil profile requires measurements or indirect determination of the six soil parameters Ks, θs, θr, n, λ, and α; evaluation of a regional water balance in the vadose zone requires long-term monitoring of soil water contents, meteorological variables, and groundwater levels. This leads to the observation that the timeframe of a study often will increase if the spatial scale of its conceptual model becomes larger. Although the measurement of fracture widths at depth is no simple matter, it takes less time than the many years of monitoring key environmental parameters needed to assess the water balance of a watershed. Moreover, while measurements of fracture widths and the Van Genuchten soil parameters will yield estimates of their true values within relatively small confidence limits that can be used in a deterministic manner, the nature of environmental parameters often gives studies at areal scales a stochastic character. The results of such studies frequently have to rely more on statistical interpolations of field measurements than on well determined causal and physical relationships. For given weather conditions in a specific soil profile, the changes of soil water fluxes with depth and time can be predicted quite well once the Van Genuchten soil parameters have been determined. However, for the same weather conditions, determination of regional groundwater recharge using Equation 5.7 will become a stochastic exercise using statistical techniques for the interpolation and averaging of soil physical and meteorological measurements. For this reason, areal-scale methods can only yield reliable results if the averaging process does not create havoc with the true flow mechanisms.
Our heuristic approach for the discussion of the three different conceptual models and their respective scales suggests an increasing spatial dimension from pore, to Darcian, to areal scale. Although such an increase is a common feature in many vadose zones, there are also hydrological observations that demonstrate at least some overlap between the spatial dimensions of the three distinctive scales. For example, a Darcian approach can be applied to soil volumes as small as a few cubic millimeters, while the Navier-Stokes equations in principle can be used to describe water flow through pores with diameters of centimeters. A Darcian
TABLE 5-1 Scales, Conceptual Models, Critical Parameters, and Measurements Relevant to Flow Mechanisms in the Vadose Zone
|
Spatial Scale |
Domain |
Conceptual Model |
Physical Model |
Critical Parameters |
Smallest Temporal Measurements |
Scale |
|
Pore |
Macropores, Fractures |
Fluid Continuum |
Hagen-Poisseuille Equation 5.1 |
Fracture Width |
Thin sections, NMR |
Minutes Days |
|
Darcian |
Laboratory, Soil Profiles |
Representative Volume |
Darcy-Buckingham Equation 5.3 |
Hydraulic Properties |
TDR, Neutron Attenuation, Tensiometers |
Hours Months |
|
Areal |
Field, Local Depression, Landscape Element |
Mass Balance |
Mass Balance Equation 5.7 |
Weather, Soil Moisture |
Meteorological Station, TDR, Neutron Attenuation, Remote Sensing, Groundwater Level |
Days Years |
approach may be quite appropriate for a large uniform landscape element covering squares of kilometers but fail on a meter scale in a heterogeneous environment. An areal water balance approach can be applied to volumes as small as a flower pot as well as to areas covering an entire continent. For this reason we have chosen names for the spatial scales that reflect their link with a particular physical model rather than a spatial dimension.
FLOW MECHANISMS AT DIFFERENT SCALES
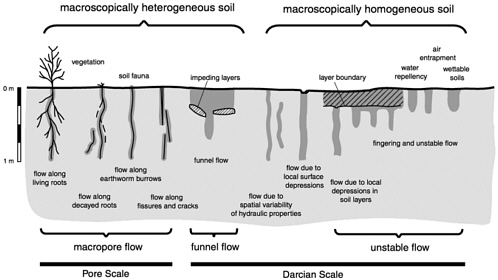
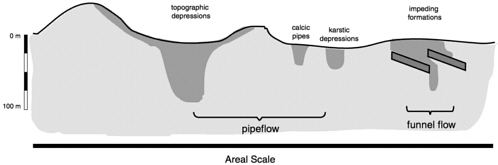
Water flow in the vadose zone occurs at different spatial and temporal scales under a wide variety of conditions. This makes it problematic to classify vadose zone flow mechanisms in a consistent manner. Another complicating factor is that processes at the pore scale determine processes at larger scales. For these reasons we have selected a practical classification criterion based upon the three conceptual models discussed in the previous section which lead to three typical spatial scales often encountered in vadose zone studies. The pore scale deals with water flow processes described by Hagen-Poiseuille's equations, the Darcian scale with processes considered to take place within fictitious representative volumes and described by Darcy's equation, and the areal scale with processes affected by major landscape elements such as local depressions, faults, and discontinuous layers in the vadose zone. Sometimes processes at the areal scale can be described quantitatively using Darcy's law in numerical models such as HYDRUS2D, while in more complicated situations only a qualitative approach is feasible. Figure 5-1 and Figure 5-2 illustrate the different flow mechanisms and their relation to the spatial scale. On the pore scale, we observe several types of macropore flow and at the Darcian scale, stable wetting as well as funnel and unstable flow (Figure 5-1). On the areal scale, we observe preferential flow due to localized recharge caused by topographic depressions, pipe flow, and funnel flow (Figure 5-2).
Pore Scale
The lucidity of the Hagen-Poiseuille Equation 5.1 makes the pore scale very attractive for the investigation of water flow through soils and rocks since the only material parameter needed for its application is the pore size. Unfortunately, its application is only practical in materials with a relatively simple pore geometry, such as capillary tube models (Bear, 1972; Scheidegger, 1974), network models (Dullien, 1992; Luxmoore and Ferrand, 1992), fractures (Bear, 1993; Rasmussen, 1987; Schrauf and Evans, 1986), and macropores.
There is abundant evidence that many soils are susceptible to rapid water flow through macropores. Macropores are often defined in terms of a specific radius (Luxmoore, 1981; Beven and German, 1982); however, no accepted general definition of a macropore exists. The definition of a specific radius is rather
arbitrary, and for operational purposes in this paper we consider a macropore to be a pore or fracture considerably larger in radius than the bulk of the pores and fractures in the porous soil or rock. In unsaturated porous media, macropores do not necessarily conduct large amounts of water. Two conditions must be met in order for macropores to contribute to rapid water flow. First, the macropore must be partially or completely filled with water, and, second, the pore needs to continuously extend over a significant portion of the porous medium. Obviously, the definition of a significant distance depends on the system of interest, and therefore the relevance of macropore flow might be very different depending on the spatial and temporal scale of interest. For instance, one common type of macropore flow in soils is flow through earthworm burrows or root channels. Earthworm burrows are typically 1-3 mm in diameter and can extend up to 6 m in vertical length. As such, water and chemicals can bypass the topsoil by traveling in earthworm burrows, and pollutants and pesticides can potentially contaminate shallow groundwater resources. When earthworm burrows end at a certain depth, water and dissolved chemicals will leave the macropore and flow through the porous matrix, thus slowing down vertical migration considerably. It is rather unlikely that continuous vertical flow paths extend over several dozens of meters in unsaturated soil, and therefore macropore flow will stop at a certain depth. The bypass of the topsoil, however, has serious consequences for many contaminants because sorption and degradation processes are usually strongest in the topsoil and cease with increasing soil depth.
Several dye tracing studies have demonstrated that macropore flow is rather common in many agricultural soils, particularly in fine-textured soils with a pronounced soil structure (Bouma et al., 1977; Flury et al., 1994; Germann, 1990; Mohanty et al., 1998; Petersen et al., 1997; Stamm et al., 1998). Out of 14 different soils investigated, Flury et al. (1994) found a majority of soils susceptible to macropore flow. Typical flow patterns observed are shown in Figure 5-3. Depending on whether the macropores are more planar or cylindrical in shape, the flow patterns appear more areal or linear, respectively.
The process of macropore flow is depicted in Figure 5-4. When the overall water input from precipitation or irrigation, q*(t), exceeds infiltration capacity of the soil, i(t), a horizontal overland flow, o(t), is generated that causes a water flux into the macropores, q(0, t). This flux causes water content inside the macropore, w(z, t), to increase. A fraction of the water, r, that occupies a macropore at a given depth will be absorbed by the soil matrix through the macropore walls. The remainder will percolate downwards into the macropore, q(z, t). The interplay of precipitation or irrigation rates with dynamics of the infiltration rate over time add to the macropore flow mechanism complexity. For example, the infiltration rate of a soil depends not only on the time since infiltration started but also on antecedent water content (Philip, 1969). When the infiltration rate, i(t), decreases with time and with increasing antecedent soil water content, the opportunity for overland flow, o(t), and macropore flow, q(0, t) increases.

FIGURE 5-3 Typical macropore flow patterns observed in structured, fine-textured soils. Patterns depict vertical cross sections of soil profiles after sprinkling irrigation of 40 mm dye solution. The horizontal bar in the left graph indicates the maximum excavation depth. After Flury, M., H. Flühler, W. A. Jury, and J. Leuenberger, 1994. Susceptibility of soils to preferential flow of water: A field study. Water Resources Research 30: 1945-1954. Copyright by American Geophysical Union.
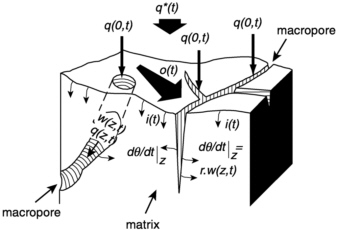
FIGURE 5-4 Schematic presentation of fluxes occurring during infiltration into a macroporous soil: q*(t) represents overall water input (precipitation, irrigation); i(t) represents infiltration into the topsoil matrix; o(t) represents short duration/short distance overland flow when q*(t) > i(t); q(0, t) represents volume flux density into the soil macropores (q(0, t) > 0 when o(t) > 0); q(z, t) and w(z, t) represent volume flux density and volumetric soil moisture, respectively, in the macropore system; r.w(z, t) represents water sorbance from macropores into the soil matrix. Note: All volume flux densities are per crosssectional area for the entire soil. From Beven, K., and P. Germann, 1982. Macropores and water flow in soils. Water Resources Research 18: 1311-1325. Copyright by American Geophysical Union.
Macropore flow is usually initiated when a portion of the soil matrix reaches saturation or at least is close to saturation in order to exceed the water entry potential of the macropore. This phenomenon can occur during an infiltration event, for instance, when the water front reaches textural boundaries. An example of such preferential flow initiation at textural boundaries is shown in Plate 4. In this experiment, conducted by Forrer et al. (1999), water was infiltrated under two different rates, 5 and 25 mm/day. A dye tracer was applied as a line source to the soil surface to visualize the flow patterns. Under the high infiltration rate, the water front started to pond at the layer boundary between plow horizon and subsoil at about 20 cm depth, and water tended to enter macropores. As a consequence, the tracer pulse split into several pulses, and channeled through a smaller cross section of the subsoil. In contrast, under the low infiltration rate, no ponding occurred at the layer boundary, and water and tracer movement followed rather uniform pathways. Horizontally and vertically averaged concentration distributions, also shown in Plate 4, depict multimodal characteristics under the high
infiltration rates typical for macropore flow. Much smoother and unimodal distributions were observed under the low infiltration rate.
Another example is presented by Germann (1986), who analyzed drainage responses to storms observed during a 7-year period in the Coshocton monolith lysimeters (Northeast Experimental Watershed, USDA-ARS, Coshocton, Ohio). Rains of only 10 mm/day caused a drainage response at 2.4 m depth on the same day as precipitation when volumetric water content in the upper 1 m of the undisturbed profile exceeded a threshold value of 0.3 m3/m3, whereas at soil water contents below this threshold value, storms greater than 50 mm/day were found not to cause any drainage flow.
Many experimental studies have confirmed the dependency of macropore flow on infiltration rates and water contents of the soil (Flury et al., 1994). The occurrence of macropore flow has always been reported in conjunction with pronounced soil structure, such as earthworm burrows, root channels, or fractures. Recent numerical analyses, however, have shown that preferential flow can also occur in macroscopically homogeneous soils with spatially variable hydraulic properties, but no pronounced macropore structure.
There is still considerable uncertainty about the physics of water flow in macropores in soils. Experiments indicate that macropores might not need to be completely filled with water in order to be conductive for water flow. Dye tracing studies by Bouma et al. (1977) and Bouma and Dekker (1978) indicate that water flows through only a small portion of planar macropore voids. Li and Ghodrati (1994) observed preferential flow of NO3 in laboratory columns at water fluxes well below the flux expected for completely water-filled macropores. This might indicate the water could flow as film flow at macropore walls.
Darcian Scale
Experimental evidence (Darcy, 1856) and theoretical considerations (Bear 1972) have proven that Darcy's empirical Equation 5.3 is valid for the exploration of flow conditions in the vadose zone using the conceptual model of a representative volume at the Darcian scale. Indeed, under many conditions this concept yields very satisfactory results, although sometimes creative adaptations are required. The most straightforward application is found under stable flow conditions characterized by horizontal wetting fronts parallel to the soil surface. For example, Figure 5-5 shows a stable wetting front in a loam soil along the Rio Salado near Socorro observed in August, 1995, a few days after heavy rainfall. Wierenga et al. (1991) have observed stable wetting fronts during long-term infiltration experiments in desert profiles near Las Cruces. In addition, many infiltration studies under controlled conditions in laboratory columns and lysimeters indicate that stable flow is a common phenomenon.
A special case of stable flow takes place during flow through stony soils. During the last 60 years, theoretical studies and experimental investigations of

FIGURE 5-5 Stable wetting front in a loam soil along the Rio Salado near Socorro observed in August, 1995, after a few days with heavy rainfall. The wetting was exposed after the river bank collapsed shortly before the picture was taken by Hendrickx..
water flow through the vadose zone have focused on agricultural soils, while our knowledge of stony soils remained limited. However, stony environments are widespread in river bed and mountain-front hydrogeological provinces that are characterized by recharge infiltration through stony layers (Issar and Passchier, 1990). Channeling of water flow through stony soils has been quantified by Hendrickx et al. (1991), who evaluated travel times through a 100-m-deep, stony vadose zone in Baluchistan (Pakistan). They found that such stony zones shorten recharge travel times considerably. For example, yearly net infiltration by an artificial recharge of 40 cm would take 35 years to reach the water table at a depth of 100 m in a sand loam without stones, but only 17 years in the same soil with 60 percent stones. Likewise, Buchter et al. (1995) observed highly irregular water flow through a stony soil monolith of 77 percent (per weight) gravel. Only a small fraction of the cross-sectional area appeared to be active in water flow.
One of the least understood preferential pathway flow mechanisms is that of unstable flow. A stable wetting front is a horizontal front that moves downwards without breaking into fingers. The behavior of such a front can be simulated by one-dimensional computer models. Unstable wetting fronts start out as horizontal wetting fronts that, under certain conditions, break into fingers or preferential flow paths as the front moves downwards, much like rain running off a sheet of glass and breaking into streams. These fingers facilitate recharge flow and transport of contaminants to the groundwater at velocities many times those calculated if a stable horizontal front is assumed. For example, in a bromide tracer experiment, Hendrickx et al. (1993) measured in the field that after 5 weeks with 120
mm precipitation, bromide concentrations in the groundwater are 6 to 13 times higher under unstable wetting fronts than under stable wetting fronts.
The occurrence of what we now recognize as unstable wetting fronts has been reported in the literature since the beginning of this century (Deecke, 1906). Similar observations were later reported by Gripp (1961) on the island of Amrum in Germany, by Gees and Lyall (1969) on Cape Sable Island in Nova Scotia (Canada), and in The Netherlands by Schuddebeurs (1957), Mooij (1957), Lopes de Leao (1988), and Raats (1984). The conditions under which unstable wetting fronts form in the field are not yet fully understood, because systematic investigations of the phenomena in field soils have been rare. However, theoretical work (Du et al., 2001; Glass et al., 1989a, 1989c, 1991; Hillel and Baker, 1988; Parlange and Hill, 1976; Philip, 1975a, 1975b; Raats, 1973; Tabuchi, 1961) supported by laboratory experiments (Baker and Hillel, 1990; Diment and Watson, 1985; Glass et al., 1989b, 1990; Hill and Parlange, 1972; Selker et al., 1989, 1992; Tamai et al., 1987; White et al., 1977; Yao and Hendrickx, 1996, 2001) indicate that fingered flow may occur under the following conditions: (1) infiltration of ponded water with compression of air ahead of the wetting front; (2) water-repellent soils; (3) continuous nonponding infiltration; and (4) in layered soil profiles where coarse-textured soil layers are overlain by less permeable layers. We will present examples of these scenarios.
Air Entrapment
Compression of air below a wetting front has been shown to cause instability of the front. For example, Wang et al. (1998) observed in a series of laboratory experiments that air entrapment can cause an otherwise stable wetting front to break up into fingers.
Water-Repellent Soils
Dry soils readily absorb water because of a strong attraction between the mineral particles and water. However, the affinity of soils for water can be reduced by hydrophobic organic materials that are either mixed with the soil particles or form a coating around them. Such soils are called hydrophobic or water-repellent, and are found in many parts of the world under a variety of climatic conditions (De Bano, 1981; Jamison, 1969; Jaramillo et al., 2000; Mallik and Rahman, 1985; McGhie and Posner, 1980; Miyamoto et al., 1977; Richardson, 1984; Rietveld, 1978). When dry, water movement is severely limited and, consequently, precipitation will not infiltrate uniformly. Indeed, field evidence for irregular wetting patterns and considerable soil water content variation have been reported in water-repellent field soils by Bond (1964), De Bano (1969a, 1969b), Dekker and Jungerius (1990), Emerson and Bond (1963), Letey et al. (1975), and Meeuwig (1971).
Field studies (Dekker and Ritsema, 1994a, 1994b; Hendrickx et al., 1993; Ritsema et al., 1993; Ritsema and Dekker, 1994) and results from lysimeter experiments (Hendrickx and Dekker, 1991) demonstrate that the irregular and incomplete wetting pattern in water-repellent soils can be predicted and explained by unstable wetting front theory. Figure 5-6 demonstrates the extreme variability in volumetric water content for the top layer of a water-repellent soil. In flat areas, dry water-repellent topsoils will accelerate natural recharge since the infiltrated water is traveling through preferential flow paths toward the aquifer (Van Dam et al., 1990). However, on slopes, water repellency may enhance runoff and reduce recharge.
On the basis of numerous field observations and measurements of soil water content and bromide content, Ritsema et al. (1993) derived a conceptual model for unstable flow (Figure 5-7). Although their study deals with unstable flow in water-repellent soils, it appears valid wherever unstable flow takes place. They recognize not only preferential flow paths with patches of dry soil between them, but also a distribution layer and a divergence layer. The distribution layer receives the precipitation and feeds by lateral flow the preferential flow paths below it. The divergence layer is located underneath the preferential flow paths and laterally distributes the water and solute fluxes. Therefore, it is to some extent counteracting the rapid transport through the preferential flow paths.
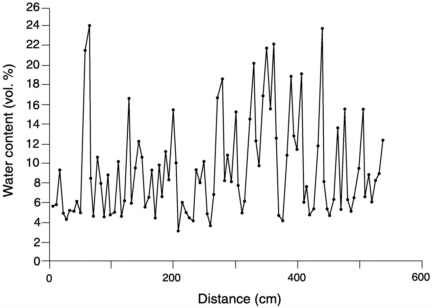
FIGURE 5-6 Variation in volumetric water content along a 5.5-m transect in a waterrepellent soil at 0.08 m depth. From Hendrickx and Dekker (1991).

FIGURE 5-7 Conceptualization of unstable flow mechanism in a water-repellent soil. From Ritsema, C. J., L. W. Dekker, J. M. H. Hendrickx, and W. Hamminga, 1993. Preferential flow mechanism in a water-repellent sandy soil. Water Resources Research 29: 2183-2193. Copyright by American Geophysical Union.
Nonponding Infiltration
The infiltration theories of Green and Ampt (1911) and Philip (1969) predict sharp, stable wetting fronts during infiltration in dry, homogeneous wettable soils. These theories were mostly verified in laboratory columns with diameters of a few centimeters, but also in field soils after periods with precipitation (Hendrickx and Yao 1996; Figure 5-5 of this chapter). However, many observers (Deecke, 1906; Raats, 1984) noted field phenomena that appear to contradict the universal validity of these infiltration theories. A lysimeter experiment was thus conducted (Hendrickx and Dekker, 1991) to demonstrate that preferential flow paths observed in wettable dune sands are not caused by local runoff, soil cracks, or macropores. A nonweighing lysimeter (height 1.2 m, width 1.4 × 1.2 m) was carefully filled with wettable dune sand and, successively, exposed to 403 mm natural precipitation during a period of four months. The lysimeter was then sampled layer by layer. The wetted soil volume decreased from 100 percent at the surface to 22 percent at 30 cm depth. Between depths 40-80 cm only 11 percent of the soil had been wetted, a clear indication for preferential flow paths. Because the lysimeter surface was perfectly horizontal and careful packing had excluded the existence of macropores, the observed preferential flow paths are without doubt a result of unstable wetting (Figure 5-8).

FIGURE 5-8 Unstable wetting patterns at 0.20 m depth in wettable sand after 403 mm precipitation; dark spots are wet. From Hendrickx and Dekker (1991).
Layered Soil Profiles
Another common field situation with a potential for fingered flow is found where a less permeable layer overlies a more permeable layer. The occurrence of unstable wetting under these conditions has been demonstrated by laboratory experiments (Glass et al., 1990; Hill and Parlange, 1972; White et al., 1977) and field observations (Starr et al., 1978, 1986). Starr et al. (1978) also conducted a controlled experiment in an undisturbed soil column (diameter 1.8 m, height 3.6 m) with a sandy loam (0.0-0.6 m) overlying a gravelly coarse sand (0.6-3.0 m). They observed uniform flow through the top layer and fingered flow in the bottom layer, where twelve distinct fingers occupied only 5 percent of the total cross-sectional area at 1.0 m depth.
Spatial Variability of Hydraulic Properties
A different type of preferential flow may be caused by spatial variability of hydraulic properties. Roth (1995) simulated water flow in a variably saturated Miller-similar medium, where local heterogeneities were represented by a spatially correlated random field of scaling factors. Under steady-state water flow, distinct flow patterns developed, with regions of high flux and regions of low flux. The flow patterns observed depended on the magnitude of the steady water flux, and consequently on the water content of the porous medium. Interestingly, two states of hydraulic structures were identified, separated by a critical point: high-flux regions developed under high flow rates corresponded to low-flux regions under low flow rates, and vice versa. Qualitative comparisons showed that these types of simulations can represent many experimental observations reported from large-scale field experiments (Roth and Hammel, 1996).
Funnel Flow
A special case of preferential flow at the Darcian scale is caused by redirection of water at soil textural boundaries, a phenomenon commonly called funnel flow. Gardner and Hsieh (1959) demonstrated impressively how coarse sand or aggregate layers embedded in a finer textured soil can funnel water flow through a small fraction of the soil profile. Figure 5-9 shows a sequence of an infiltration event where unsaturated water flow is redirected at an inclined sand lens embedded in a finer texture soil material. A field experiment, conducted by Kung (1990), showed that such embedded coarse sand layers can funnel water flow through 1 percent of the soil matrix.
Flow Through Small Displacement Faults in Sand
There is evidence that faults in sand are relatively common features in tectonically active extensional regions like the Rio Grande rift. Because fault-zone
deformation typically decreases the pore size, it decreases the saturated hydraulic conductivity. However, under unsaturated conditions the actual unsaturated hydraulic conductivity is likely to be greater than that of the adjoining undisturbed sand layers in regions with low soil water contents. It is hypothesized that fault zones can become preferred flow paths under the arid conditions of the south-western United States (John Wilson, Laurel Goodwin, and Peter Mozley, written communication, 1996; Sigda, 1997). Figure 5-10 shows preferential wetting of conjugate faults in a sand near Socorro, New Mexico, after a period of precipitation.
Areal Scale
Just as the complexity of the pore geometry makes it all but impossible to use the Hagen-Poiseuille equation to describe flow through a real porous medium, the complexity of some landscape elements often makes it all but impossible to use a Darcian approach. We will illustrate this with four typical situations.
Karstic Vadose Zone
Gunn (1983) investigated mechanisms by which flow is concentrated and transmitted to the underlying aquifer for a karst area in the Waitomo district of

FIGURE 5-10 Displacement faults in sand near Socorro, New Mexico. The wet spots coincide with the faults. From J.M. Herrin (September 1997).
New Zealand. Mean annual precipitation and potential evapotranspiration in the study area are 2,370 mm and 775 mm, respectively. Gunn found that closed depressions (solution dolines, sinkholes, cockpits) act as funnels and collect near surface water through three concentrating mechanisms: (1) overland flow, defined as any water flowing along the ground surface; (2) throughflow, defined as any water flowing laterally within the soil; and (3) subcutaneous flow, defined as water flowing laterally through the upper, weathered layer of limestone.
Three vertical flow mechanisms were recognized for water transmission through the vadose zone: (1) film flow (named shaft flow by Gunn), defined as water flowing underground as films on the walls of vertical shafts; (2) fracture or macropore flow (named vadose flow by Gunn), defined as vertically moving water that flows for a major part of its course in enlarged joints and fractures; (3) vadose seepage, defined as vertically moving water that percolates through small, tight joints and fissures or as intergranular flow. Gunn (1983) combined these six flow mechanisms into a conceptual vadose zone flow model (Figure 5-11) and qualitatively validated it by determining water travel times for each flow mechanism using measurements of water temperature and calcium and magnesium ion
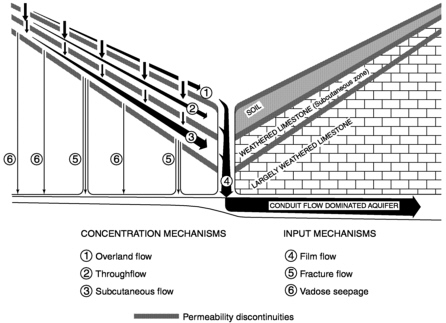
FIGURE 5-11 Idealized cross section of a closed depression showing flow concentration and mechanisms (arrows proportional to water flow in Waitomo depressions). After Journal of Hydrology, 61, Gunn, J., Point-recharge of limestone aquifers: A model from New Zealand karst, pp. 19-29, 1983, with permission from Elsevier Science.
concentrations. This validation revealed the principal characteristics for each model component.
Overland flow is quantitatively insignificant in the Waitomo district, while subcutaneous flow appears to supply more water to vertical shafts than does throughflow. Travel times for subcutaneous and throughflow vary between 0 and 14 weeks with a mean of approximately 6 weeks. The concentration of near surface water makes film flow more important than fracture flow, while vadose seepage contributes less than 5 percent to aquifer recharge. Two different categories of fracture flow were identified: flows through open joints and fissures, and flows through soil-filled fissures. The first responded directly to rainfall with a mean travel time of less than a week, whereas the second had a mean travel time of 8 weeks. The travel times for vadose seepage varied between 0 and 19 weeks, indicating that part of the water flows rapidly through small fractures as macropore flow while the remainder flows slowly through the porous material as capillary flow. Although Gunn (1983) cautions that in other climate-soil-regolith regimes the relative importance of these flow mechanisms may be different, his conceptual model and field observations offer considerable insight to the dynamics of flow processes through fractured rocks. Striking is the fact that capillary flow accounts for less than 5 percent of recharge volume.
Simultaneous Occurrence of Fast and Slow Flow
The simultaneous occurrence of capillary and macropore flow within the same soil mass without the presence of clearly defined macropores appears to be quite typical. Under these conditions macropore flow cannot be detected from visual observations in the field, but is inferred from analysis of solute profiles or drainage responses at the groundwater table.
Johnston (1987) used solute profiles in combination with groundwater table measurements to demonstrate macropore flow in a deep clayey regolith in south-west Western Australia. The regolith showed marked heterogeneity over horizontal and vertical distances of only a few meters, which resulted in a complex water movement pattern. Thirteen vertical concentration profiles of natural chloride were used to estimate recharge rates through the 16-m-deep unsaturated vadose zone. Although over most of the 700 m2 experimental area recharge rates varied from 2.2-7.2 mm/year, a small portion of the site had rates between 50 and 100 mm/year. As a result of this preferred flow, a groundwater mound was observed in piezometer 1356 below the localized recharge area within 12-14 h of intense rainstorms and dissipated over a period of 2-4 days (Figure 5-12).
Scanlon (1992) demonstrated the existence of preferred pathway flow through fissured sediments in the Chihuahuan desert of Texas, with annual precipitation of 280 mm and approximate potential evapotranspiration of 3,000 mm. The term fissure refers to the alignment of discontinuous surface collapse structures, or gulleys where the underlying extensional feature is filled with sediment.
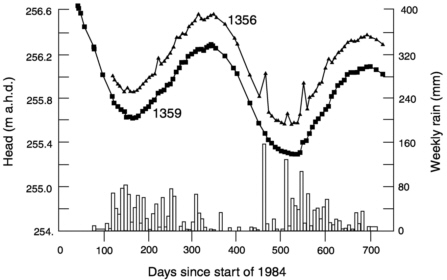
FIGURE 5-12 Variation in weekly precipitation and potentiometric head in piezometers 1359, located where capillary flow dominates, and 1356, located where macropore flow occurs. After Journal of Hydrology, 94, Johnston, C. D., Preferred water flow and localized recharge in a variable regolith, pp. 129-142, 1987, with permission from Elsevier Science.
A somewhat unexpected result from Scanlon's study is that water fluxes calculated from vertical chloride profiles in the fissured sediments ranged from 1-8 mm/year and were as much as 350 times higher than those calculated for adjacent ephemeral stream sediments. This difference could not be attributed to differences in soil texture since fissures and ephemeral streams have similar textures varying from muddy, sandy gravel to loamy sand and clay loam. However, open cavities and fractures in the fissured sediments were filled with loose sediments to give lower bulk densities and looser soil structure, so that fast macropore flows are promoted rather than slow capillary flows. Much of the precipitation occurring as high-intensity convective summer storms infiltrates to depths of only 0.1-0.3 m in the ephemeral stream beds and is readily lost by evapotranspiration, whereas deep infiltration in the fissured sediments prevents such losses and results in a much larger recharge rate.
Localized Recharge
In comparison to direct recharge, localized and indirect recharge are often considered at least as significant, if not the most important sources, of natural
recharge in arid and semiarid lands (Gee and Hillel, 1988; Lerner et al., 1990; Stephens, 1994; Wood and Sanford, 1995). Localized recharge implies horizontal movement of surface and/or near-surface water and occurs in weathered bare hardrock or limestone terrain, topographical depressions, minor wadis or arroyos, and in mountain front systems. To account for localized recharge it is necessary to measure or estimate local runoff and runon volumes so that these can be included in the water balance. Such estimates and measurements are often complicated by subsurface components of runoff and runon flow (Anderson and Burt, 1990) and by the fact that they frequently occur on a scale too detailed to map for engineering studies (Lerner et al., 1990).
A classical example of localized recharge occurs in the numerous depressions dotting the Great Plains of North America. These features can measure tens to thousands of meters across, are often occupied by wetlands or lakes, and are referred to as “potholes,” “sloughs,” or “playas.” Meyboom (1966) was one of the first investigators to quantify localized recharge during a one-year study of a till plain pothole with a watershed contributing area of 0.8 ha in south-central Saskatchewan (Canada). His pothole has a bottom diameter of 40 m and the height of its surrounding rim varies between 3 and 8 m. It was determined that the pothole or local depression, with 15 percent of the total surface area, contributed 70 percent of the recharge. Other investigators have also reported studies that confirm the large contribution of localized recharge described by Meyboom (1966); examples are Freeze and Banner (1970), Miller et al. (1985), and Winter (1986). Using chemical techniques, Wood and Sanford (1995) estimated that approximately half (4-5 mm/year) the annual recharge (9-10 mm/year) to the Ogallala Aquifer on the southern High Plains in the United States occurs through playa floors that cover only 6 percent of the area.
The effects of topographic, soil, and climatic conditions on the magnitude of depression-focused recharge for specific sites is difficult to measure in the field. Therefore, Nieber et al. (1993) and Boers (1994) have developed mathematical models. Nieber et al. (1993) assumed for simplicity that their catchment was circular in form and contained a circular-shaped depression with a single drainage outlet. Boers (1994) developed a similar procedure for the design of rainwater harvesting catchments in arid and semiarid zones that can also be used for the assessment of localized recharge. His method is based on actual evapotranspiration predictions using a numerical soil water balance model, while the runoff component is predicted by a runoff model (Boers et al., 1986). The microcatchment in Figure 5-13 illustrates how the components of rainwater harvesting interact. A microcatchment consists of a runoff area with a maximum flow distance of 100 m and an adjacent basin area (the depression) with a tree, bush, or row crop. The objective of rainwater harvesting is to induce runoff, collect and store the water in the basin area, and conserve it in the root zone for consumptive use by the vegetation. The components shown in Figure 5-13 yield the following water balance on an annual basis:
D = P + R − Ei − Ew − Eact − Tact − ΔW (5.8)
where D is deep percolation or recharge, P is precipitation, R is runoff calculated over the basin area where it is collected, Ei is evaporation of water intercepted by the vegetation, Ew is open water evaporation, Eact is the evaporation from bare soil, Tact is actual transpiration by the vegetation, and ΔW is the increase in soil water storage in the root zone. Table 5-2 presents the annual water balance components at Sadoré (Niger) for one Neem tree in a basin of 8 m2 with a soil profile comprising 3 m fine sand above 2 m laterite gravel. If the basin receives no runon water, no recharge takes place during a dry, average, or even a wet year. In a dry year, runoff areas of 20 and 40 m2 do not generate any recharge, although they do increase actual transpiration and, thus, the growth rate of the tree. In an average year a modest increase in runoff area from 20-40 m2 produces a 22-fold increase in recharge from 5-113 mm, whereas in a wet year a similar increase in area ratio produces a 4-fold increase in recharge from 38-185 mm. These and other model studies by Tosomeen (1991) demonstrate the great sensitivity of localized recharge to rather small changes in topography, soil type, and climate.

FIGURE 5-13 Microcatchment consisting of runoff area and basin area with tree. Rainfall induces runoff, which collects in the basin area where the water infiltrates, is stored, and is available for root water uptake and transpiration. In the basin area, losses occur by interception, soil evaporation, and deep percolation below the root zone. After Boers (1994).
TABLE 5-2 Annual Precipitation (P), Predicted Runoff (R), Actual Transpiration (Tact), and Recharge (D) (mm) for One Neem Tree in a 8 m2 Basin at Sadoré, Niger, for Precipitation Only and for Precipitation and Runoff from 20 m2 and 40 m2 Runoff Areas in Three Precipitation Years (Boers, 1994)
|
Rainfall Only |
Rainfall and Runoff |
||
|
Average Year |
Runoff area 20 m2 |
Runoff area 40 m2 |
|
|
P |
545 |
545 |
545 |
|
R |
0 |
232 |
465 |
|
Tact |
409 |
633 |
755 |
|
D |
0 |
5 |
113 |
|
Dry Year |
Runoff area 20 m2 |
Runoff area 40 m2 |
|
|
P |
258 |
258 |
258 |
|
R |
0 |
78 |
155 |
|
Tact |
138 |
205 |
277 |
|
D |
0 |
0 |
0 |
|
Wet Year |
Runoff area 20 m2 |
Runoff area 40 m2 |
|
|
P |
673 |
673 |
673 |
|
R |
0 |
285 |
571 |
|
Tact |
481 |
720 |
849 |
|
D |
0 |
38 |
185 |
Pipes Through Calcic Horizons
The La Mesa surface in southwestern New Mexico has developed on Rio Grande deposits mainly consisting of sands and gravels. The surface was abandoned by the Rio Grande River during the middle Pleistocene and since that time a calcic soil with an indurated calcic horizon has formed. A characteristic of such an indurated calcic horizon is the presence of dissolution pipes that develop through the horizon to the underlying sediments. Most of the upper soil profile has been eroded, exposing the calcic horizon. However, in the last few hundred years the exposed calcic horizon has been covered with sand dunes with a loamy sand texture. The sand has taken the form of coppice dunes that develop underneath the shrub vegetation. Consequently, the pipes in the carbonate horizon are mostly buried underneath 0.5-1.5 m of loamy sand and are very difficult to identify from the surface. Rodríguez-Marín and Hendrickx observed in October 1998 on the La Mesa surface pipe densities from one per 14-38 m2 along two transects of 5.6 and 3.2 km in a 2.2-m-deep trench dug for a gas pipeline (Figure 5-14). Since the pipes cover approximately 15-18 percent of the total surface, the ratio between catchment area (around the pipe) and through flow area (inside the pipe) varies from about 7 to 5 on the La Mesa surface. It is anticipated that such
localized pipes serve as preferential flow conduits for water flow and may increase groundwater recharge by an order of magnitude.
Since 1998, Harrison and Hendrickx have observed many pipes in highway cuts near Hatch and Albuquerque and along escarpments with exposed calcic horizons near Socorro and El Paso. These field observations along a 400-km-long stretch from El Paso to Albuquerque indicate that pipes through indurated calcic horizons are widespread in New Mexico and West Texas.
MEASUREMENT OF PREFERENTIAL FLOW PHENOMENA
Preferential flow phenomena are difficult to measure. Often, preferential flow is inferred from unexpectedly early water and chemical breakthrough or from unexpectedly deep water and chemical migration in the vadose zone. Bimodal or multimodal chemical concentration profiles are often interpreted as a result of preferential flow. Such measurements, even when preferential flow inference is very plausible, only give indirect evidence of the causal flow mechanisms. More direct evidence can be obtained by staining techniques with dyes or water, which have been extensively used to visualize preferential flow at the pore scale, such as macropore and fracture flow (Bouma et al., 1977), and preferential flow at the Darcian scale, such as unstable (Glass et al., 1988; Hendrickx et al., 1988) or funnel flow (Gardner and Hsieh 1959; Kung, 1990). Probably the most accurate quantitative measure of macropore flow is obtained through intercepting macropores with tubing to collect the throughflow (Edwards et al., 1989).
Macropore and fracture flow are often experimentally quantified by using tension infiltrometers. When infiltrating water is under negative pressure, flow through macropores and fractures can be more or less controlled according to the Laplace equation. The fraction of macropores of different sizes can thereby be measured by using a series of infiltration tests with different tensions (Watson and Luxmoore, 1986). More recently, tomographic techniques and nuclear magnetic imaging have been applied to visualize complicated pore structures and associated flow phenomena (Heijs et al., 1996; van As and van Dusschoten, 1997). Such techniques, and improvements thereof in the future, will help elucidate the preferential flow mechanisms at the pore scale and at those Darcian scales that cover centimeters and decimeters.
At larger spatial scales covering entire fields or landscape elements, flow phenomena are indirectly assessed by measuring soil moisture and soil structure through remote sensing, ground-penetrating radar, neutron-probe moisture measurements, and other geophysical techniques that allow large-scale mapping of pedological and geological features. Deep coring tests analyzed for chloride distributions often provide insight into flow mechanisms. The most convincing evidence for preferential flow at large spatial scales comes from visual observations, such as the pipes through calcic horizons in New Mexico (Figure 5-14) or the potholes in the Great Plains (Meyboom, 1966). Such structures are testimony
to long-term persistent preferential flow processes that lead to the formation of observable landscape features.
FORMULATION OF CONCEPTUAL MODELS
The formulation of criteria for determining whether a conceptual model is an adequate characterization for a specific vadose zone is extremely complicated since there are so many factors that affect flow mechanisms. Nevertheless, the case studies presented in this review have a number of general characteristics in common that can serve as a guideline for the development of conceptual models.
All three spatial scales of preferential flow discussed have in common that an initially spatially uniform flux is disturbed and water flow is confined to a smaller cross-sectional area of the vadose zone. Even though the mechanisms that lead to the formation of preferential flow patterns are very different, the phenomenological appearances and the environmental consequences are often very similar. Figure 5-15 depicts a schematic view of different flow regimes that can be distinguished during a preferential flow process: (1) lateral distribution flow in the attractor zone where preferential flow is initiated; (2) downward preferential flow in the transmission zone where water moves along preferential flow pathways and thus bypasses a considerable portion of the porous media matrix; and (3) lateral and downward dispersive flow in the dispersion zone where preferential flow pathways are interrupted and water flow becomes uniform again.
The attractor zone can vary considerably in thickness (Figure 5-3), and may even be the soil surface itself when preferential flow is initiated by runon into localized surface depressions. Figure 5-3, Figure 5-4, Figure 5-5, Figure 5-7, and Figure 5-14 clearly show an attractor zone located close to the soil surface. The pipe in Figure 5-14 receives water by lateral collection over the calcic horizon from the surrounding areas. Therefore, it is concluded that an attractor zone at or below the soil surface is a definitive feature of preferential flow at whatever scale it takes place.
The dispersion zone can be recognized in Figure 5-7 and Figure 5-11 but is missing in the other figures. It is often not included in graphical presentations of preferential flow when it occurs so deep in the vadose zone that water rarely even reaches this zone (Figure 5-3, Figure 5-4, Figure 5-14). Figure 5-10 shows that the dispersion zone for one layer with preferential flow can be the attractor zone for another deeper layer. Indeed, in a deep vadose zone, finding a sequence of attractor and dispersion zones is expected.
Stable flow can be considered as a flow mechanism that did not yet reach the transmission zone (Figure 5-5). This is the case, for example, where the amount of precipitation is not sufficient to wet the attractor zone to a depth that allows unstable wetting to occur (Hendrickx and Yao, 1996). Apparently stable flow can be dealt with as a special case in the general mechanism of preferential flow.

FIGURE 5-15 Schematic view of flow processes in the vadose zone. After Geoderma, 70, Flühler, H., W. Durner, and M. Flury, Lateral solute mixing processes: A key for understanding field-scale transport of water and solutes. Pp. 165-183, 1996, with permission from Elsevier Science.

FIGURE 5-16 Application of stability criteria for determination of preferential flow caused by unstable wetting fronts. After Geoderma, 70, Hendrickx, J. M. H. and T. Yao, Prediction of wetting front stability in dry field soils using soil and precipitation data, pp. 265-280, 1996, with permission from Elsevier Science.
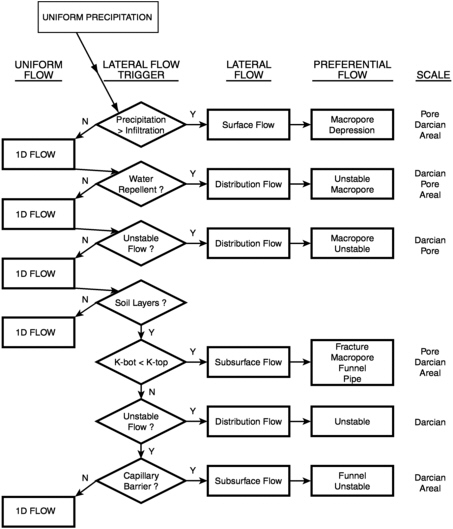
All three spatial scales of preferential flow discussed also have in common that preferential flow can start only after a certain minimum amount of precipitation has fallen at an intensity sufficiently high to cause the attractor zone to feed the transmission zone. Precipitation at a low intensity will infiltrate into the soil surface and result in a stable flow mechanism under a wide variety of conditions, from the fracture at the pore scale to the depression at the areal scale. However, a small amount of rain at a sufficiently high intensity may immediately trigger preferential flow at the pore scale as well as the areal scale. We need also to consider the effect of antecedent soil water content that affects the amount of water that can infiltrate into the soil at the surface or at the walls of a macropore. An example of how precipitation amount, precipitation intensity, and antecedent soil water content affect the occurrence of unstable flow in a wettable sand soil is given in Figure 5-16.
In Figure 5-17 we present a flow diagram for the evaluation of vadose zone conditions that will cause preferential flow at different scales as a result of a lateral flow trigger. Since precipitation is spatially uniform, it will result in uniform one-dimensional flow through the vadose zone unless a lateral flow trigger is present. We recognize different lateral flow triggers, such as a precipitation rate that exceeds the infiltration rate, vertical changes in unsaturated hydraulic conductivities where the lower layer has a lower conductivity, water repellency, and other mechanisms that cause unstable flow. Although the principles of the flow diagram are straightforward and will result in a first assessment of the propensity for preferential flow, no evaluation is complete without considering in which manner antecedent soil water content affects the flow processes in the attractor and transmission zones as a function of precipitation amount and intensity. This is the most difficult question but also the most crucial, since the threshold values for the minimum amount of precipitation and the intensity determine the occurrence of preferential flow at any scale.
REFERENCES
Anderson, M. G., and T. P. Burt, 1990. Subsurface runoff. Chapter 11 in M. G. Anderson and T. P. Burt (eds.). Process Studies in Hillslope Hydrology.
Baker, R. S., and D. Hillel, 1972. Laboratory tests of a theory of fingering during infiltration into layered soils. Soil Sci. Soc. Am. J. 54: 20-30.
Bear, J., 1972. Dynamics of Fluids in Porous Media. New York: Dover Publications, Inc., 764 pp.
Bear, J., 1993. Modeling flow and contaminant transport in fractured rocks. In: J. Bear, C. Tsang, and G. De Marsily, eds. Flow and Contaminant Transport in Fractured Rock. San Diego, Calif.: Academic Press, Inc., pp. 1-37.
Bear, J., T. Chin-Fu, and G. De Marsily (eds.), 1993. Flow and Contaminant Transport in Fractured Rock. New York: Academic Press, 560 pp.
Beven, K., and P. Germann, 1982. Macropores and water flow in soils. Water Resources Research 18: 1311-1325.
Boers, Th. M., 1994. Rainwater harvesting in arid and semi-arid zones. Wageningen, The Netherlands: International Land Reclamation and Improvement Institute (ILRI), 132 pp.
Boers, Th. M., M. De Graaf, R. A. Feddes, and J. Ben-Asher, 1986. A linear regression model combined with a soil water balance model to design micro-catchments for water harvesting in add zones. Agricultural Water Management 11: 187-206.
Bond, R. D., 1964. The influence of the microflora on the physical properties of soils . II. Field studies on water repellent sands. Australian Journal of Soil Research 2: 123-131.
Bouma, J., and L. W. Dekker, 1978. A case study on infiltration into dry clay soil. I. Morphological observations. Geoderma 20: 27-40.
Bouma, J., A. Jongerius, O. Boersma, A. Jager, and D. Schoonderbeek, 1977. The function of different types of macropores during saturated flow through four swelling soil horizons. Soil Sci. Soc. Am. J. 41: 945-950.
Buchter, B., C. Hinz, M. Flury, and H. Fluhler, 1995. Heterogeneous flow and solute transport in an unsaturated stony soil monolith. Soil Sci. Soc. Am. J. 59: 14-21.
Campbell, G. S., 1985. Soil Physics with Basic, Transport Models for Soil-Plant Systems. New York: Elsevier, 150 pp.
Childs, E. C., 1969. The Physics of Soil Water Phenomena. New York: John Wiley and Sons.
Corey, A. T., 1990. Mechanics of Immiscible Fluids in Porous Media. Littleton, Colo.: Water Resources Publications, 255 pp.
Currie, I. G., 1993. Fundamental Mechanics of Fluids, 2nd ed. New York: McGraw-Hill, Inc.
Darcy, H. 1856. Les Fontaines Publique de la Ville de Dijon. Paris: Dalmont.
DeBano, L. F., 1969a. Water movement in water-repellent soils. In: Proc. Symp. on Water-repellent Soils, Riverside, California, 61-89.
DeBano, L. F., 1969b. Water-repellent soils: A worldwide concern in management of soil and vegetation. Agric. Sci. Rev. 7: 11-18.
DeBano, L. F., 1981. Water-repellent soils: A state of the art. Gen. Tech. Rep. PS-W-46, Pacific Southwest Forest and Range Experiment Station, 21 pp.
Deecke, W., 1906. Einige Beobachtungen am Sandstrande. Centralbl. für Mineral. Geol. und Paläont., 721-727.
Dekker, L. W., and P. D. Jungerius, 1990. Water repellency in the dunes with special reference to The Netherlands . Catena Suppl. 18: 173-183.
Dekker, L. W., and C. J. Ritsema, 1994a. How water moves in a water repellent sandy soil. 1. Potential and actual water repellency. Water Resources Research 30: 2507-2517.
Dekker, L. W., and C. J. Ritsema, 1994b. Fingered flow: The creator of sand columns in dune and beach sands . Earth Surface Processes and Landforms 19: 153-164.
Diment, G. A., and K. K. Watson, 1985. Stability analysis of water movement in unsaturated porous materials . 3. Experimental studies. Water Resources Research 21: 979-984.
Du, X. H., T. Yao, W. D. Stone, and J. M. H. Hendrickx. 2001. Stability analysis of the unsaturated water flow equation, 1. Mathematical derivation. Water Resources Research, in press.
Dullien, F. A. L., 1992. Porous media: Fluid transport and pore structure. New York: Academic Press, 574 pp.
Edwards, W. M., M. J. Shipitalo, L. B. Owens, and L. D. Norton, 1989. Water and nitrate movement in earthworm burrows within long-term no-till cornfields. J. Soil Water Conserv. 44: 240-243.
Emerson, W. W., and R. D. Bond, 1963. The rate of water entry into dry sand and calculation of the advancing contact angle. Australian Journal of Soil Research 1: 9-16.
Flühler, H., W. Durner, and M. Flury, 1996. Lateral solute mixing processes: A key for understanding field-scale transport of water and solutes. Geoderma 70: 165-183.
Flury, M., H. Flühler, W. A. Jury, and J. Leuenberger, 1994. Susceptibility of soils to preferential flow of water: A field study . Water Resources Research 30: 1945-1954.
Forrer, I., R. Kasteel, M. Flury, and H. Flühler, 1999. Longitudinal and lateral dispersion in an unsaturated field soil. Water Resources Research 35(10): 3049-3060.
Freeze, R. A., and J. Banner, 1970. The mechanism of natural groundwater recharge and discharge. 2. Laboratory column experiments and field measurements. Water Resources Research 6: 138-155.
Gardner, W. H., and J. C. Hsieh, 1959. Water movement in soils. Dept. of Crop and Soil Sciences, Washington State University, [Video], Pullman, Wash.
Gee, G. W., and D. Hillel, 1988. Groundwater recharge in arid regions: Review and critique of estimation methods. Hydrological Processes 2: 255-266.
Gees, R. A., and A. K. Lyall, 1969. Erosional sand columns in dune sand, Cape Sable Island, Nova Scotia, Canada. Canadian Journal of Earth Sciences 6: 344-347.
Germann, P. F., 1986. Rapid drainage response to precipitation. Hydrol. Processes 1: 3-13.
Germann, P. F., 1990. Macropores and hydrologic hillslope processes. In: M. G. Anderson and T. P. Burt, eds. Process Studies in Hillslope Hydrology, 327-363.
Glass, R. J., T. S. Steenhuis, and J.-Y. Parlange, 1988. Wetting front instability as a rapid and farreaching hydrologic process in the vadose zone. J. Contam. Hydroll. 3: 207-226.
Glass, R. J., T. S. Steenhuis, and J.-Y. Parlange, 1989a. Wetting front instability. 1. Theoretical discussion and dimensional analysis. Water Resources Research 25: 1187-1194.
Glass, R. J., T. S. Steenhuis, and J.-Y. Parlange, 1989b. Wetting front instability. 2. Experimental determination of relationships between system parameters and two-dimensional unstable flow field behavior in initially dry porous media. Water Resources Research 25: 1195-1207.
Glass, R. J., T. S. Steenhuis, and J.-Y. Parlange, 1989c. Mechanism for finger persistence in homogeneous, unsaturated, porous media: Theory and verification. Soil Sci. 148: 60-70.
Glass, R. J., J. King, S. Cann, N. Bailey, J.-Y. Parlange, and T. S. Steenhuis, 1990. Wetting front instability in unsaturated porous media: A three-dimensional study. Transp. Porous Media 5: 247-268.
Glass, R. J., J.-Y. Parlange, and T. S. Steenhuis, 1991. Immiscible displacement in porous media: Stability analysis of three-dimensional, axisymmetric disturbances with application to gravity-driven wetting front instability. Water Resources Research 27: 1947-1956.
Green, W. H., and G. A. Ampt, 1911. Studies on soil physics. I. The flow of water and air through soils. J. Agric. Sci. 4: 1-24.
Gripp, K., 1961. Über Werden und Vergehen von Barchanene an der Nordsee-Küste SchleswigHolsteins. Zeitsch. für Geomorphologi, Neue Folge 5: 24-36.
Gunn, J., 1983. Point-recharge of limestone aquifers: A model from New Zealand karst . J. Hydrol. 61: 19-29.
Hanks, R. J., and G. L. Ashcroft, 1986. Applied Soil Physics: Advanced Series in Agricultural Sciences 8. New York: Springer-Verlag, 159 pp.
Heijs, A. W., C. J. Ritsema, and L. W. Dekker, 1996. Three-dimensional visualization of preferential flow patterns in two soils. Geoderma 70: 101-116.
Hendrickx, J. M. H., L. W. Dekker, M. H. Bannink, and H. C. van Ommen, 1988. Significance of soil survey for agrohydrological studies. Agricultural Water Management 14: 195-208.
Hendrickx, J. M. H., and L. W. Dekker, 1991. Experimental evidence of unstable wetting fronts in non-layered soils . In: Proc. Natl. Symp. on Preferential Flow. Chicago, Ill. 16-17, Dec. 1991, St. Joseph, Mich.: Am. Soc. Agric. Eng., 22-31.
Hendrickx, J. M. H., S. Khan, M. H. Bannink, D. Birch, and C. Kidd, 1991. Numerical analysis of groundwater recharge through stony soils using limited data. J. Hydrol. 127: 173-192.
Hendrickx, J. M. H., L. W. Dekker, and O. H. Boersma, 1993. Unstable wetting fronts in water repellent field soils. Journal of Environmental Quality 22: 109-118.
Hendrickx, J. M. H., and T. Yao, 1996. Prediction of wetting front stability in dry field soils using soil and precipitation data. Geoderma 70: 265-280.
Hendrickx, J. M. H., and G. Walker, 1997. Recharge from precipitation. Chapter 2, In: I. Simmers, ed. Recharge of Phreatic Aquifers in (Semi)-Arid Areas. Rotterdam, The Netherlands: Balkema.
Hill, D. E., and J.-Y. Parlange, 1972. Wetting front instability in layered soils. Soil Sci. Soc. Am. J. 36: 697-702.
Hillel, D., 1998. Environmental Soil Physics. San Diego: Academic Press.
Hillel, D., and R. S. Baker, 1988. A descriptive theory of fingering during infiltration into layered soils. Soil Sci. 146: 51-56.
Issar, A., and R. Passchier, 1990. Regional hydrogeological concepts. In: D. N. Lerner et al., eds. Groundwater Recharge. International Contributions to Hydrogeology, Vol. 8, Hannover, Germany: Int. Assoc. Hydrogeologists, Verlag Heinz Heise, 21-98.
Jamison, V. C., 1969. Wetting resistance under citrus trees in Florida. In: Proc. Symp. on Water Repellent Soils, Riverside, California, 9-15.
Jaramillo, D. F., L. W. Dekker, C. J. Ritsema, and J. M. H. Hendrickx. 2000. Occurrence of soil water repellency in arid and humid climates. Journal of Hydrology 231/232: 105-114.
Johnston, C. D., 1987. Preferred water flow and localized recharge in a variable regolith . J. Hydrol. 94: 129-142.
Jury, W. A., W. R. Gardner, and W. H. Gardner, 1991. Soil Physics, New York: John Wiley and Sons , 328 pp.
Kirkham, D., and W. L. Powers, 1972. Advanced Soil Physics. New York: John Wiley and Sons , 534 pp.
Koorevaar, P., G. Menelik, and C. Dirksen, 1983. Elements of soil physics. New York: Elsevier, 230 pp.
Kung, K.-J. S., 1990. Preferential flow in a sandy vadose zone. 1. Field observation. Geoderma 46: 51-58.
Lawes, J. B., J. H. Gilbert, and R. Warington, 1881. On the amount and composition of the rain and drainage-waters collected at Rothamsted, Part I and II. J. Royal Agric. Soc. of England, London 17: 241-279.
Lerner, D. N., A. S. Issar, and I. Simmers, 1990. Groundwater Recharge. A Guide to Understanding and Estimating Natural Recharge. International Contributions to Hydrogeology, Vol. 8. Hannover: Internat. Assoc. of Hydrogeologists, Heise.
Letey, J., J. F. Osborn, and N. Valoras, 1975. Soil water repellency and the use of nonionic surfactants. Calif. Water Res. Center (Contribution 154) 85 pp.
Li, Y., and M. Ghodrati, 1994. Preferential transport of nitrate through soil columns containing root channels. Soil Sci. Soc. Am. J. 94: 653-659.
Lopes De Leao, L. R., 1988. Hé. Grondboor en Hamer 3/4: 111-112.
Luxmoore, R. J., 1981. Micro-, meso-, and macroporosity of soil. Soil Sci. Soc. Am. J. 45: 671-672.
Luxmoore, R. J., and L. A. Ferrand, 1992. Water flow and solute transport in soils: Modeling and applications . In: D. Russo and G. Dagan, eds. New York: Springer Verlag, pp. 45-60.
Mallik, A. U., and A. A. Rahman, 1985. Soil water repellency in regularly burned Calluna heathlands: Comparison of three measuring techniques. Journal of Environmental Management 20: 207-218.
Marshall, T. J., and J. W. Holmes, 1979. Soil Physics. Cambridge University Press, 345 pp.
McGhie, D. A., and A. M. Posner, 1980. Water repellency of a heavy-textured Western Australian surface soil . Aust. J. Soil Res. 18: 309-323.
Meeuwig, R. O., 1971. Infiltration and Water Repellency in Granitic Soils. U.S. Dept. of Agriculture Forest Service, Research Paper INT-111, Ogden, Utah, 20 pp.
Meyboom, P., 1966. Unsteady groundwater flow near a willow ring in hummocky moraine. J. Hydrol. 4: 38-62.
Miller, J. J., D. F. Acton, and R. J. St. Arnaud, 1985. The effect of groundwater on soil formation in a morainal landscape in Saskatchewan. Canadian Journal of Soil Science 65: 293-307.
Miyamoto, S., A. Bristol, and W. I. Gould, 1977. Wettability of coal-mine spoils in Northwestern New Mexico. Soil Sci. 123: 258-263.
Mohanty, B. P., R. S. Bowman, J. M. H. Hendrickx, J. Simunek, and M. Th. van Genuchten, 1998. Preferential transport of nitrate to a tile drain in an intermittent-flood-irrigated field: Model development and experimental evaluation. Water Resources Research 34: 1061-1076.
Mooij, J., 1957. Aeolian destruction forms on a sand beach. Grondboor en Hamer 1: 14-18.
Nieber, J. L., C. A. S. Tosomeen, and B. N. Wilson, 1993. A stochastic-mechanistic model of depression-focused recharge. In: Y. Eckstein and A. Zaporozec, eds. Hydrogeologic Inventories and Monitoring and Groundwater Modeling ., 207-229.
Parlange, J.-Y., and D. E. Hill, 1976. Theoretical analysis of wetting front instability in soils. Soil Sci. 122: 236-239.
Petersen, C. T., S. Hansen, and H. E. Jensen, 1997. Tillage-induced horizontal periodicity of preferential flow in the root zone. Soil Sci. Soc. Am. J. 61: 586-594.
Philip, J. R., 1969. Theory of infiltration. Advances in Hydroscience 5: 215-296.
Philip, J. R., 1975a. Stability analysis of infiltration. Soil Sci. Soc. Am. Proc. 39: 1042-1049.
Philip, J. R., 1975b. The growth of disturbances in unstable infiltration flows. Soil Sci. Soc. Am. Proc. 39: 1049-1053.
Raats, P. A. C., 1973. Unstable wetting fronts in uniform and nonuniform soils, Soil Sci. Soc. Am. Proc. 37: 681-685.
Raats, P. A. C., 1984. Tracing parcels of water and solutes in unsaturated zones. In: B. Yaron, G. Dagan, and J. Goldshid, eds. Pollutants in Porous Media: The Unsaturated Zone Between Soil Surface and Ground Water. Berlin: Springer, 4-16.
Rasmussen, T. C., 1987. Computer simulation model of steady fluid flow and solute transport through three-dimensional networks of variably saturated, discrete fractures. In D. D. Evans and T. J. Nicholson, Flow and Transport Through Unsaturated Fractured Rock. Geophysical Monograph 42, American Geophysical Union, Washington D.C., pp. 107-114.
Richardson, J. L., 1984. Field observation and measurement of water repellency for soil surveyors . Soil Survey Horiz. 25: 32-36.
Rietveld, J. J., 1978. Soil Nonwettability and Its Relevance as a Contributing Factor to Surface Runoff on Sandy Dune Soils in Mali. Report of project Production primaire au Sahel, Agric. Univ., Wageningen, The Netherlands, 179 pp.
Ritsema, C. J., L. W. Dekker, J. M. H. Hendrickx, and W. Hamminga, 1993. Preferential flow mechanism in a water-repellent sandy soil. Water Resources Research 29: 2183-2193.
Ritsema, C. J., and L. W. Dekker, 1994. How water moves in a water-repellent sandy soil. 2. Dynamics of fingered flow. Water Resources Research 30: 2517-2531.
Roth, K., 1995. Steady state flow in an unsaturated, two-dimensional, macroscopically homogeneous, Miller-similar medium. Water Resources Research 31: 2127-2140.
Roth, K., and K. Hammel, 1996. Transport of conservative chemical through an unsaturated two-dimensional Miller-similar medium with steady state flow. Water Resources Research 32: 1653-1663.
Scanlon, B. R., 1992. Moisture and solute flux along preferred pathways characterized by fissured sediments in desert soils. J. of Contaminant Hydrol. 10: 19-46.
Scheidegger, A. E., 1974. The physics of flow through porous media. Toronto: University of Toronto Press .
Schrauf, T. W., and D. D. Evans, 1986. Laboratory studies of gas flow through a single natural fracture. Water Resources Research 19: 1253-1265.
Schuddebeurs, A. P, 1957. Cone sand and sandstone. Grondboor en Hamer. 2. 21-25.
Selker, J. S., T. S. Steenhuis, and J.-Y. Parlange, 1989. Preferential flow in homogeneous sandy soils without layering. Paper No. 89-2543, Am. Soc. Agric. Eng., Winter Meeting, New Orleans, La., 22 pp.
Selker, J. S., T. S. Steenhuis, and J.-Y. Parlange, 1992. Wetting front instability in homogeneous sandy soils under continuous infiltration. Soil Sci. Soc. Am. J. 56: 1346-1350.
Sigda, J. M., 1997. Effects of small-displacement faults on the permeability distribution of poorly consolidated Santa Fe Group sands, Rio Grande Rift New Mexico. M.S. thesis, New Mexico Tech, Socorro.
Snow, D. T., 1969. Anisotropic permeability of fractured media. Water Resources Research 5: 1273-1289.
Stamm, C., H. Flühler, R. Gächter, J. Leuenberger, and H. Wunderli, 1998. Preferential transport of phosphorus in drained grassland soils. J. Environ. Qual. 27: 515-522.
Starr, J. L., H. C. DeRoo, C. R. Frink, and J.-Y. Parlange, 1978. Leaching characteristics of a layered field soil. Soil Sci. Soc. Am. J. 42: 386-391.
Starr, J. L., J.-Y. Parlange, and C. R. Frink, 1986. Water and chloride movement through a layered field soil. Soil Sci. Soc. Am. J. 50: 1384-1390.
Stephens, D. B., 1994. A perspective on diffuse natural recharge mechanisms in areas of low precipitation. Soil Sci. Soc. Am. J. 58: 40-48.
Streeter, V. L., E. B. Wylie, and K. W. Bedford, 1988. Fluid Mechanics, 9th ed. Boston: McGraw-Hill.
Tabuchi, T., 1961. Infiltration and ensuing percolation in columns of layered glass particles packed in laboratory. Nogyo dobuku kenkyn, Bessatsu. Trans. Agr. Eng. Soc., Japan, 1, 13-19 (in Japanese, with a summary in English).
Tamai, N., T. Asaeda, and C. G. Jeevaraj, 1987. Fingering in two-dimensional, homogeneous, unsaturated porous media . Soil Sci. 144: 107-112.
Tosomeen, C. A. S., 1991. Modeling the effects of depression focusing on groundwater recharge . M.S. thesis, Dept. of Agricultural Engineering, University of Minnesota.
Van As, H., and D. van Dusschoten, 1997. NMR methods for imaging of transport processes in micro-porous systems . Geoderma 80: 389-403.
Van Dam, J. C., J. M. H. Hendrickx, H. C. van Ommen, M. H. Bannink, M. Th. Van Genuchten, and L. W. Dekker, 1990. Simulation of water and solute transport through a water-repellent sand soil, J. Hydrol. 120: 139-159.
Van Genuchten, M. Th., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44: 892-898.
Van Genuchten, M. Th., F. J. Leij, and S. R. Yates, 1991. The RETC code for quantifying the hydraulic functions of unsaturated soils. EPA/600/2-91/065. R. S. Kerr Environ. Res. Lab., U.S. Environmental Protection Agency, Ada, Okla., 93 pp.
Wagenet, R. J., 1998. Scale issues in agroecological research chains. Nutrient Cycling in Agro-ecosystems 50: 23-34.
Wagenet, R. J., J. Bouma, and J. L. Hutson, 1994. Modelling water and chemical fluxes as driving forces in pedogenesis . In R. B. Bryant, R. W. Arnold, and M. R. Hoosbeek, eds. Quantitative Modelling of Soil Forming Processes. SSSA Special Publ. 39, ASA/CSSA/SSSA, Madison,Wis., pp. 17-35.
Wang, Z., J. Feyen, M. Th. Van Genuchten, and D. R. Nielsen, 1998. Air entrapment effects on infiltration rate and flow instability. Water Resources Research 34: 213-222.
Watson, K., and R. J. Luxmoore, 1986. Estimating macroporosity in a watershed by use of a tension infiltrometer . Soil Sci. Soc. Am. J. 50: 578-582.
Wheatcraft, S. W., and J. H. Cushman, 1991. Hierarchical approaches to transport in heterogeneous porous media . In: U.S. National Report to International Union of Geodesy and Geophysics, Rev. Geophysics (supplement), pp. 263-269, American Geophysical Union. Washington, D.C.
White, I., P. M. Colombera, and J. R. Philip, 1977. Experimental studies of wetting front instability induced by gradual change of pressure gradient and by heterogeneous porous media. Soil Sci. Soc. Am. J. 41: 483-489.
Wierenga, P. J., R. G. Hills, and D. B. Hudson, 1991. The Las Cruces trench site: Characterization, experimental results, and one-dimensional flow predictions. Water Resources Research 27: 2695-2705.
Winter, T. C., 1986. Effect of ground-water recharge on configuration of the water table beneath sand dunes and on seepage in lakes in the sandhills of Nebraska , USA. J. Hydrol. 86: 221-237.
Wood, W. W., and W. E. Sanford, 1995. Chemical and isotopic methods for quantifying groundwater recharge in a regional, semiarid environment. Ground Water 33: 458-468.
Yao, T., and J. M. H. Hendrickx, 1996. Stability of wetting fronts in homogeneous soils under low infiltration rates. Soil Science Society of America Journal 60: 20-28.
Yao, T., and J. M. H. Hendrickx, 2001. Stability analysis of the unsaturated water flow equation: 2. Experimental Verification. Water Resources Research, in press.