6
Modeling Macropore Flow in Soils: Field Validation and Use for Management Purposes
Nicholas Jarvis1 and Martin Larsson1
ABSTRACT
This paper reviews the development and application of models to predict the impact of preferential flow in the unsaturated zone on nonpoint-source pollution of groundwater and surface waters by agrochemicals, focusing mainly on the effects of macropores in structured soils. A brief review of the various modeling approaches that have been adopted is first presented. We then discuss the use of macropore flow models for management and regulatory purposes, focusing especially on data requirements and procedures for field validation and parameter estimation for predictive applications. Results of field-scale tests of one widely used macropore flow model (MACRO) are presented as a case study to illustrate the consequences of macropore flow for nitrate and pesticide leaching to shallow groundwater.
It is concluded that regulatory use of macropore flow models is necessary, but such use requires transparency and uniformity of approach to ensure that simulations are free of subjective bias. Regulatory applications of macropore flow models should be based either on precalibrated scenarios or on objective automatic parameter estimation routines (pedotransfer functions). Recommendations and procedures currently under development for use of the MACRO model in E.U. harmonized pesticide registration are also described.
|
1 |
Department of Soil Sciences, Swedish University of Agricultural Sciences, Uppsala, Sweden |
INTRODUCTION
Nonequilibrium or preferential flow of water enhances the risk of leaching of surface-applied contaminants to receiving water bodies, since much of the buffering capacity of the biologically and chemically reactive topsoil may be bypassed. In this way, chemicals can quickly reach subsoil layers where degradation and sorption processes are generally less effective. The term “preferential flow” implies that recharge is concentrated to a small fraction of the total pore space where vertical flow rates are much faster than rates of lateral equilibration with slowly moving resident soil water (Flühler et al., 1996). For example, in structured soils, nonequilibrium flow in soil macropores (e.g., shrinkage cracks, worm channels, old root holes) may dominate the soil hydrology, especially in fine-textured soils, where they operate as high-conductivity flow pathways bypassing the impermeable soil matrix (Beven and Germann, 1982). Preferential flow also occurs in structureless sandy soils in the form of unstable wetting fronts or fingering (Hillel, 1987), although this aspect of nonequilibrium flow behavior is not discussed further in this paper.
This paper reviews the development and application of models to predict the impact of macropore flow in the soil unsaturated zone on nonpoint-source pollution of groundwater and surface waters, focusing especially on agrochemicals. A brief review of the various modeling approaches that have been adopted is first presented. The dual-porosity model MACRO (Jarvis, 1994a; Jarvis and Larsson, 1998) is briefly described, and results of field tests of the model are presented that illustrate the consequences of macropore flow for nitrate and pesticide leaching. Concepts of model validation and calibration are discussed, and the data requirements for field validation of macropore flow models are reviewed. Current trends and recommendations for use of these models in pesticide registration procedures are also described.
MACROPORE FLOW: PHYSICAL PRINCIPLES
Macropores are large, continuous, structural pores that constitute preferred flow pathways for infiltrating water in most soils. At the macroscopic scale of measurement, this is reflected in large increases in unsaturated hydraulic conductivity across a small soil water pressure head range close to saturation (Clothier and Smettem, 1990; Jarvis and Messing, 1995). At the pore scale, macropore flow is generated when the water pressure locally increases to near saturation at some point on the interface with the surrounding soil matrix, such that the waterentry pressure of the pore is exceeded. Macropore flow can be sustained if the vertical flux rates in the macropore are large in relation to the lateral infiltration losses into the matrix due to the prevailing capillary pressure gradient. This is most likely to be the case in clay soils with an impermeable matrix. These lateral losses can be further restricted by relatively impermeable interfaces between
macropores and the bulk soil, including cutans on aggregate surfaces and organic linings in biotic pores (Thoma et al., 1992). Thus, macropore flow can sometimes be significant even in lighter-textured soils of large matrix hydraulic conductivity.
The impact of macropore flow on solute transport depends strongly on the nature of the solute ion under consideration, particularly the size of the molecule as it affects lateral spreading between pore domains by diffusion, its sorption characteristics, and the nature of source/sink terms (i.e., biological transformations) affecting the transport process. For example, the effects of macropore flow on leaching are opposite for solutes that are foreign to the soil (e.g., pesticides) compared to indigenous solutes produced within the soil (e.g., nitrate mineralization from organic matter, without fertilizer applications). In the former case, macropore flow may strongly increase leaching losses, while in the latter case, leaching should be decreased by macropore flow (Jarvis, 1998).
CURRENT APPROACHES TO MODELING MACROPORE FLOW IN SOILS
In this section, some existing models accounting for macropore flow are described. This review is not intended to be exhaustive, but rather to give some idea of the different types of models available, their advantages and limitations, and their potential as management tools. Most existing models take a macroscopic, continuum approach by lumping individual preferential flow pathways in the soil into two or more pore domains within a one-dimensional numerical scheme. A large number of models of this type have been developed in recent years. They vary with regard to the number of flow domains considered (two-domain or multidomain models), the degree of simplification and empiricism involved in process descriptions (e.g., functional vs. mechanistic models), and also the manner in which exchange between flow domains is represented. In the following sections, some of these existing models are described.
Functional Models
In recent years, a number of simple empirical (or functional) models have been developed that can account for preferential flow (Addiscott, 1977; Corwin et al., 1991; Hall, 1993; Nicholls and Hall, 1995). Barraclough (1989a) described a simple three-region model based on a capacity (“tipping bucket”) approach to describe water flow, the mobile-immobile water concept to characterize solute transport in two domains (see next section), and a simple instantaneous bypass routine to account for macropore flow. The model was apparently implemented only for nonreactive solute transport, although it was compared to nitrate leaching data during three winter seasons (Barraclough, 1989b).
Some functional models may be rather limited in their ability to simulate preferential flow due to simplifications in the treatment of soil water flow. For example, these models usually assume that water outflow from each soil layer is zero until filled to field capacity. Thus, rapid and deep-penetrating bypass flow in dry, macroporous soils cannot be simulated. Difficulties may also be caused by the fact that the normal time step in these models is one day, whereas an appropriate time scale to characterize preferential flow and transport processes would be of the order of hours, or even minutes.
Dual-Porosity/Single Permeability Models
Analytical models have been developed based on the two-region (mobileimmobile water) convection-dispersion equation (CDE) for both nonreactive and sorbing and degrading solutes (van Genuchten and Wierenga, 1976; van Genuchten and Wagenet, 1989; Gamerdinger et al., 1990). These analytical solutions of the CDE require idealized initial and boundary conditions and assume steady-state water flow. Thus, although such approaches may provide some theoretical insights into solute transport processes occurring in structured soils, they are not appropriate to field situations characterized by time-varying soil water content due to evaporation, root water uptake, and intermittent inputs of rainfall. For this reason, their use as management tools is rather limited.
Numerical solutions of the mobile-immobile water concept have also been implemented. However, even when the mobile-immobile water CDE is solved numerically, it is often either coupled to Richards' equation or steady water flow is assumed (Lafolie and Hayot, 1993; Zurmühl and Durner, 1996). Such an approach only provides at best a partial description of nonequilibrium flow and transport phenomena, since it cannot account for rapid movement of infiltrating water in macropores to depth in dry soil. For transient conditions, one unresolved question is how best to define the fractional mobile water content in relation to the time-varying total water content. Zürmuhl and Durner (1996) discussed this problem and recommended defining a variable ratio between the mobile water content and the total water content based on the shape of the hydraulic conductivity function, such that the conductivity at the boundary between mobile and immobile water represented a constant fraction of the conductivity at the current water content. Van Dam et al. (1990) presented a simple solution of the mobile-immobile water CDE, coupled to Richards' equation, which may be appropriate to waterrepellent soils where a part of the soil remains unwetted during infiltration.
Jarvis (1989) and Armstrong et al. (1995) described a model particularly suited to cracking clay soils. In this model (CRACK), vertical water flow and solute transport occur in a crack system that is defined, for each layer in the soil profile, by a fixed spacing and a porosity that varies due to swelling and shrinkage. Vertical transport is neglected in the soil aggregates, which act as sinks for water and sources/sinks for solute. In the case of solute, the aggregates are di-
vided into numerical slices and lateral diffusion and exchange is modeled explicitly using Fick's law. In the latest version of the model, subroutines have been implemented to describe nitrate transformations and pesticide sorption and degradation (Armstrong et al., 1995).
Dual-Porosity/Dual-Permeability Models
In these models, two pore domains are each characterized by a porosity, a water pressure (and water content), and solute concentration. In contrast to the mobile-immobile water approach, vertical water flow and solute transport are calculated for both domains, with mass exchange between domains treated as source/sink terms in the one-dimensional (vertical) model structure. This mass exchange between domains is calculated using approximate first-order equations, based either on an effective diffusion pathlength related to the macroscale soil geometry (aggregate size) or empirical mass transfer coefficients.
Gerke and van Genuchten (1993a) described a model of water flow and nonreactive solute transport based on the van Genuchten/Mualem model for the soil hydraulic functions (van Genuchten, 1980; Mualem, 1976), applied to a bimodal pore size distribution (Othmer et al., 1991; Durner, 1992). Richards' equation and the CDE are used to calculate water flow and solute transport, respectively, in both pore domains, while mass exchange of water and solutes is calculated using approximate first-order equations accounting for both convective and diffusive transfer (Gerke and van Genuchten, 1993b). Due to the geometry of the flow system, the rate of mass exchange between the domains is inversely proportional to the square of an effective diffusion pathlength (van Genuchten, 1985; Youngs and Leeds-Harrison, 1990).
Jarvis (1994a) and Jarvis and Larsson (1998) described a dual-porosity model (MACRO) in which Richards' equation and the convection-dispersion equation are used to model soil water flow and solute transport in soil micropores, while a simplified capacitance-type approach is used to calculate water and solute movement in macropores. This description of gravity-driven water flow in macropores can be considered as the numerical equivalent of the analytical kinematic wave model described by Germann (1985). Later in this paper, some case studies are presented of field applications of MACRO. Therefore, this particular model is now described in more detail.
In MACRO, a simple cut-and-join or two-line method is used to define the hydraulic functions (Smettem and Kirkby, 1990), rather than the additive superimposition of two pore regions employed, for example, by Gerke and van Genuchten (1993a). The “boundary” between the two pore domains is defined by the air-entry pressure head in the Brooks and Corey (1964) equation, with an equivalent water content and hydraulic conductivity defining the saturated state of the micropores (Figure 6-1). The boundary condition at the soil surface is an important part of any flow and transport model. In MACRO, a flux boundary
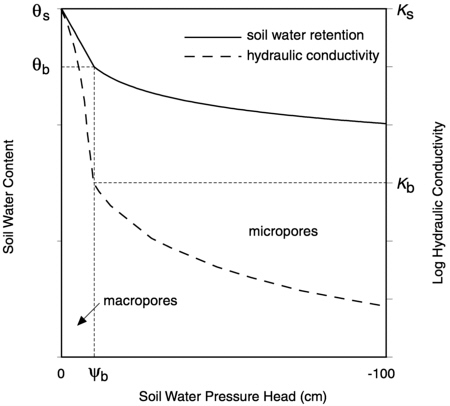
FIGURE 6-1 Schematic representation of soil hydraulic functions in the MACRO model: Ks is the saturated hydraulic conductivity, θs is the saturated water content, ψb is the pressure head defining the boundary between macropores and micropores, θb is the equivalent water content, and Kb is the hydraulic conductivity at ψb. From Larsson and Jarvis (1999b).
condition is used to partition incoming rainfall between the two pore regions depending on the infiltration capacity of the micropores. With respect to solute transport, the water infiltrating in macropores is characterized by a concentration cma* calculated assuming complete mixing with solute stored in the solution phase of a shallow “mixing” depth zd:

(6.1)
where Qs is the amount of solute stored in the top layer of the soil, Δz is the layer thickness, R is the net rainfall, cr is the concentration in the rain, θ and γ are the water content and bulk density in the top layer, and f is the fraction of sorption sites in the macropore region.
Water and solute exchange rates between the flow domains (Mw and Ms, respectively) are calculated as a function of an effective diffusion pathlength d, using approximate physically based first-order expressions (Booltink et al., 1993; Gerke and van Genuchten, 1993b). For solute, both diffusive and convective mass transfer are considered:
(6.2)
and
(6.3)
The subscripts ma and mi refer to macropores and micropores, θb is the saturated water content of the micropores (Figure 6-1), γw is a scaling factor introduced to match approximate and exact solutions to the diffusion problem (van Genuchten, 1985), c′ is the solute concentration in either macropores or micropores depending on the direction of convective transfer, De is an effective diffusion coefficient, and Dw is an effective water diffusivity given by:
(6.4)
where Dθb and Dθmi are the water diffusivities at θb and θmi, respectively, and Sma is the degree of saturation in the macropores, which is introduced to account for the effects of incomplete wetted contact area between the two pore domains.
A full water balance is considered in MACRO, including precipitation, evapotranspiration, and root water uptake; deep seepage; and lateral fluxes to tile drains in saturated soil. Solute transport and transformation processes in the model include convective-dispersive transport, Freundlich equilibrium sorption with sorption sites partitioned between the two pore domains, microbial degradation according to first-order kinetics, plant uptake, and canopy interception/washoff.
Multiporosity/Multipermeability Models
Steenhuis et al. (1990) described a simple multidomain model of solute movement based on a piecewise linear approximation to the hydraulic conductivity function and the assumption of a unit hydraulic gradient. Solute exchange between pore classes is calculated by mixing a fixed fraction of the water and solute in each pore class in a common pool before being redistributed. If the
mixing fraction is set to zero, the multidomain model reduces to a parallel streamtube model, whereas if it is set to unity (complete lateral mixing), it becomes equivalent to the CDE.
Hutson and Wagenet (1995) described a multiregion model of water flow and solute transport (TRANSMIT) based on the existing single-domain model LEACHM (Wagenet and Hutson, 1987). TRANSMIT can be used to investigate the impacts of preferential flow occurring at the porescale (e.g., macropore flow) by simulating multiple pore domains, and also physical nonequilibrium induced by soil heterogeneity through modeling multiple, interacting soil columns. A wide range of solutes can be dealt with, including pesticides and nitrate. Convective and diffusive mass exchange between all combinations of columns and/or pore domains is calculated using empirical expressions.
Gwo et al. (1995) described a multiporosity model of water flow and solute transport (MURF/MURT) based on the overlapping pore continua concept (Gerke and van Genuchten, 1993a). Richards' equation and the CDE are used to model transport in each pore domain, while water exchange is regulated by empirical exchange coefficients in simple first-order expressions. Solute exchange is driven by both convective transfer and first-order diffusive exchange.
Multiporosity models can, of course, default to the dual-porosity case when required, and there may be good reasons for doing so. As the number of pore classes in the model increases, the description of mass exchange processes necessarily becomes more uncertain and less mechanistic. Thus, although multidomain models may provide valuable insights into the nature of solute transport in heterogeneous soils, and also allow much greater flexibility in matching the observed behavior of solute transport in soil compared to two-domain models (Gwo et al., 1995), they may require extensive calibration and cannot easily be used predictively for management purposes (Hutson and Wagenet, 1995).
Two-Dimensional Models
Nieber and Misra (1995) described a two-dimensional, dual-porosity, finite element model of water flow and nonreactive solute transport in tile-drained soil. The mass exchange terms between the domains were taken from Gerke and van Genuchten (1993a, 1993b). A sensitivity analysis for the model was presented showing how chemical mass flux arriving at the drains was strongly regulated by the strength of interaction between the domains.
APPLICATION OF MACROPORE FLOW MODELS
Model Validation
Regulatory authorities and other management users must have confidence in the output of macropore flow models if these are to be used as tools to aid
decision-making. This implies that the model must be considered sufficiently valid or validated in the minds of the users for the intended purpose. It is often claimed, from a logical and philosophical point of view, that models cannot be validated because they are only ever approximations to reality, and because the truth of theory cannot be proven (Oreskes et al., 1994). However, this widely held belief is based on a rather narrow view of what constitutes validation. A pragmatic alternative definition can be summarized by the truism that all models are wrong, but some are useful (see reviews by Rykiel, 1996, and Steefel and van Cappellen, 1998). It is helpful here to distinguish between conceptual validity, which involves subjective judgement, and model validation, which should be an objective procedure. Conceptual validity implies that the model concepts, simplifications, and assumptions are considered justifiable and reasonable for the stated use of the model, based on a consensus of understanding in the scientific community. Of course, it is always possible to criticize some aspects of the theoretical or conceptual basis of any model, since all models are to a greater or lesser extent simplifications of reality. Thus, operational model validation is a necessary procedure that identifies the limits and conditions of conceptual validity. Thus, operational validation is the process of determining whether the model meets specified performance criteria, defined as the level of accuracy required for a given purpose and context of use. In an interesting review of the concept and practice of model validation, Rykiel (1996) stated that “validation is not a procedure for testing scientific theory or for certifying the ‘truth' of current scientific understanding. Validation means that a model is acceptable for its intended use because it meets specified performance requirements.” Seen in this light, operational validation is a rigorous quantitative procedure similar to hypothesis testing in statistics. It is also the process by which model concepts gain credibility for a given use or, after repeated testing, are ultimately rejected in favor of what are perceived to be improved descriptions. Thus, conceptual validity can only be achieved by extensive and repeated operational validation.
The importance of context of use can be demonstrated by a simple example. Richards' equation and the CDE may be conceptually valid for predicting water flow and solute transport in homogeneous porous media, but would repeatedly fail operational validation tests for predicting leaching to groundwater in naturally heterogeneous soils, and lose credibility for this purpose.
Apart from difficulties with semantics, one reason for the continuing confusion over the meaning and purpose of model validation is that there are no widely accepted, standard, objective performance criteria for testing models (Rykiel, 1996). In statistics, a probability level of 0.05 is often used as a test of significance. This is an arbitrary standard, but widely accepted. Similar standard measures are required for operational model validation. In this respect, it is important that representatives of the user-community (regulatory authorities, industry) take an active role in specifying performance criteria, simply because the level of accuracy required depends on the use of the model and the target quantity being
predicted (i.e., concentrations, loads, average values, maximums). The confusion that arises when performance criteria for model validation are not clearly expressed a priori can be demonstrated by the current situation in the European Union with respect to harmonized pesticide registration procedures. E.U. directives state that models “validated at the community (E.U.) level” are to be used to predict environmental concentrations in soil, groundwater, and surface waters. However, validation is not defined, nor are any criteria specified for assessing validity. This has led to a situation where a large number of different models are being used by regulators and industry, with considerable confusion (and costs) resulting from the very wide range of different predictions that are possible.
Model Calibration
The success of the operational validation procedure depends critically on distinguishing between conceptual errors and parameter errors (Loague and Green, 1991). As noted above, conceptual errors result from incorrect or undue simplification of process descriptions in the model and also neglect of significant processes (Russell et al., 1994). Clearly, some degree of conceptual error is inevitable, since models necessarily represent simplifications of reality. However, in principle, these should be minimized when mechanistic process descriptions are used (Wauchope, 1992) and in detailed models that include as many relevant processes as possible. Parameter error is the use of inappropriate parameter values. These errors arise either because the required data are not available or because the measurements are themselves subject to error and/or uncertainty due to spatial and temporal variability, or can be interpreted ambiguously, or for some other reason do not adequately reflect the prevailing field conditions. These errors may be potentially serious for detailed simulation models and for those parameters for which the relevant model outcome (e.g., leaching) is especially sensitive. Calibration is the process of minimizing parameter error in order to determine the extent of conceptual error, and is normally the first step in operational validation. Calibration is needed for all but the simplest models because direct measurements of all input parameters are rarely if ever available, either because of lack of time or money, or because the parameter is too difficult, too variable, or in many cases, impossible to measure. Bearing in mind the need for calibration, it is vital that field data utilized for operational validation meet certain quality criteria.
Data Requirements for Model Validation
The data required for model validation can be divided into two groups: measurements of model input parameters, and corroboratory validation measurements of the state of the system to be modeled. As a general rule, the modeler must be constrained as far as possible by both sets of measurements, such that the
degree of freedom during model calibration is minimized. Ideally, for macropore flow and transport models, the parameterization should be based on actual measurements of soil water retention and unsaturated hydraulic conductivity, including the critical pressure head range close to saturation. In this way, parameters defining the hydraulic properties of the macropore region can be determined by curve-fitting the model functions to measurements made across an appropriate range of pressure heads (Jarvis et al., 1999).
The modeler must also be constrained by detailed measurements of the state of the system to be modeled (i.e., validation data). In this respect, it is especially critical that, as far as possible, (1) complete measured mass balances are available for both water and the solute of interest, and (2) both resident concentrations/amounts and solute fluxes are measured. This is because resident and flux concentrations will differ considerably if macropore flow is a significant process. Also, coring methods alone cannot reliably detect preferential movement of strongly sorbing and degrading solutes, since only small (though environmentally significant) amounts are transported. This is because the analytical detection limits for resident concentrations obtained by core samples are relatively high, and the spatial variability of the solute distribution is often large in relation to the sampling intensity. In contrast, flux measurements give a measure of integrated transport for larger areas. Thus, ideally, measurements should be made of changes of both water and solute storage in the soil unsaturated zone, together with gains and losses from the system at the soil surface and at some depth in the soil, preferably below the maximum rooting depth. Storage measurements should be made with a high spatial resolution, both vertically and laterally, while flux measurements at the boundaries should be made with a high temporal resolution to capture the rapid and dynamic nature of macropore flow processes. The requirement for flux measurements means that either lysimeter or field-scale experiments on monitored tile-drainage systems are preferred. As an example of the latter, the nonreactive tracer experiment and model application reported by Larsson and Jarvis (1999a) can serve as a useful example to illustrate the range of field data required to properly validate macropore flow models such as MACRO. The measurements utilized by Larsson and Jarvis (1999a) are listed in Table 6-1, together with the spatial and temporal resolution achieved in each case. The results of this application of the MACRO model are discussed in the following section.
Case Studies with the MACRO Model
The MACRO model is probably the most widely used and tested model dealing with macropore flow in the unsaturated zone. Applications of the model to field and lysimeter experiments concerning nonreactive tracer movement, salt leaching from salinized soils, and pesticide leaching have been reported by, among others, Saxena et al. (1994), Jarvis et al. (1994), Andreu et al. (1994, 1996), Jarvis (1995), Jarvis et al. (1995), Gottesbüren et al. (1995), Bergström
TABLE 6-1 Field Measurements Utilized by Larsson and Jarvis (1999a)
|
Component |
Measurement |
Resolution |
|
Surface boundary |
Precipitation Meteorological variables Solute application |
Hourly Daily averages 30 collector trays to estimate mean and spatial variability of bromide spray application |
|
Storage changes |
Water and bromide |
8 to 12 replicate cores, on 6 occasions following application during a 1-year period samples taken at 10-cm-depth intervals to 90-cm depth |
|
Fluxes |
Drainflow at 1-m depth Bromide concentrations in drainflow |
Continuous Every 1.5 mm of drainflow |
|
Bottom boundary |
Bromide concentrations in groundwater at 2-m depth |
Weekly |
(1996), Besien et al. (1997), Bourgault de Coudray et al. (1997), Beulke et al. (1998), Villholth and Jensen (1998), Jørgensen et al. (1998), and Jarvis et al. (2000). One of the most comprehensive field tests of the MACRO model to date was reported by Larsson and Jarvis (1999a, 1999b), who compared model predictions with measurements of bromide, herbicide, and nitrate leaching to tile-drains in a structured silty clay soil in Sweden. Bromide and the weakly sorbing herbicide bentazone were applied together to bare soil in autumn 1994, and the subsequent leaching from a 0.4-ha plot monitored during a one-year period (Larsson and Jarvis, 1999a). Model predictions of nitrate leaching were compared with measurements made during an eight-year period on an adjacent plot at the same site (Larsson and Jarvis, 1999b). These experiments and model applications are now discussed in more detail.
Site Hydrology and Nonreactive Transport
A reasonable description of the site hydrology is a prerequisite for accurate predictions of solute transport (Armstrong et al., 1996). Therefore, as a first step in the model application, Larsson and Jarvis (1999a) compared model predictions and measurements of drain discharge, concentrating especially on estimating soil macroporosity (θs-θb) and saturated hydraulic conductivity by matching the timing and shape of individual flow hydrographs (i.e., time to peak flows and recessions). These parameters were estimated by calibration even though some direct measurements were available. This is because the drain response predicted by the
model is highly sensitive to these parameters, which in turn are normally characterized by large spatial and temporal variability. Model predictions were checked against water content profiles measured on six occasions during a one-year period, and were found to be satisfactory. In the second stage of model calibration, estimates of sensitive parameters regulating the impact of macropore flow on preferential solute transport, particularly the mixing depth, zd(Equation 6.1), and the effective diffusion pathlength, d (Equations 6.2 and 6.3), were obtained by comparing model predictions and measurements of the initial bromide breakthrough to the drains occurring 26 days after application. Figure 6-2 shows that
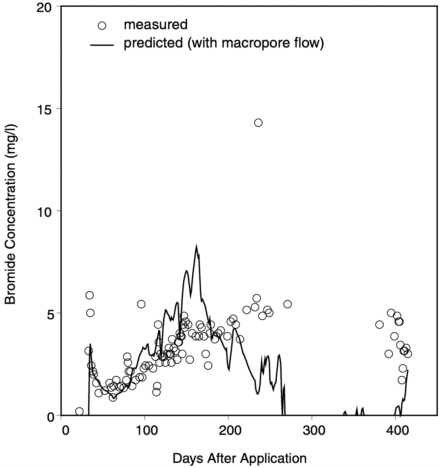
FIGURE 6-2 A comparison of bromide concentrations measured in tile drainage outflow at Lanna with those simulated by the MACRO model. Redrawn from Journal of Hydrology, 215, Larsson, M. H., and N. J. Jarvis, Evaluation of a dual-porosity model to predict field-scale solute transport in macroporous soil, pp. 153-171, 1999, with permission from Elsevier Science.
the model was able to capture reasonably well the initial breakthrough of bromide due to macropore flow, and also the subsequent slower convective-dispersive movement of bromide through the matrix, assuming d values of 150, 100, and 300 mm in topsoil and upper and lower subsoil horizons, respectively. The initial rapid breakthrough to tile drains was accompanied by significant bromide concentrations measured in groundwater at 2-m depth (10 µg 1−1 measured 42 days after application). The model accurately matched the timing of this response in the groundwater, but the concentrations were somewhat underestimated (3 µg 1−1). The model satisfactorily matched the observed distributions of bromide in the soil profile throughout the one-year period following application (see Figure 6-3 for one example), but only if a rather large pore volume for anion exclusion was assumed for this clayey textured soil (23 percent). It is interesting to note that, even without macropore flow, the model could have been calibrated to achieve an excellent fit to the bromide profiles (for example, by changing the anion exclusion volume), because the proportion of the dose moving deep into the soil by macropore flow was quite small (about 10 percent) and the variability in the measured profiles was quite large. However, it would not be possible to match the pattern of flux concentrations observed in tile-drain outflow without considering macropore flow. This emphasizes that validation of macropore flow models requires measurements of both resident and flux concentrations, and that without flux measurements, there is a clear risk that misleading positive conclusions can be drawn concerning the validity of models that do not account for preferential movement.
Pesticide Leaching
Following this calibration, the model was validated by comparing model predictions and measurements of bentazone concentrations in tile drain outflow (Figure 6-4) and resident concentrations in the soil profile (Figure 6-5), with no changes to the parameterization of soil hydraulic functions. Figure 6-4 shows that the very weakly sorbed herbicide bentazone (koc = 5 cm3 g−1) behaved rather similarly to bromide, so that a more complete validation of the model for the Lanna site ought to include a more strongly sorbed solute. Nevertheless, the dual-porosity approach does seem to accurately reflect field-scale solute transport in this well-structured soil. Model simulations were also run without macropore flow by setting the effective diffusion pathlength to 1 mm (nominal zero), thereby ensuring complete equilibrium between the pore domains. A comparison of these simulation results enables the impact of macropore flow to be quantified. Figure 6-4 and Figure 6-5 show that in the Lanna soil, macropore flow results in the rapid movement of a small pulse of applied herbicide, deep in the soil, but that this bypass flow also effectively reduces the rate of convective movement of the bulk of the compound in the matrix. This retardation is especially significant because the longer transit time of the compound in the topsoil results in much larger degradation
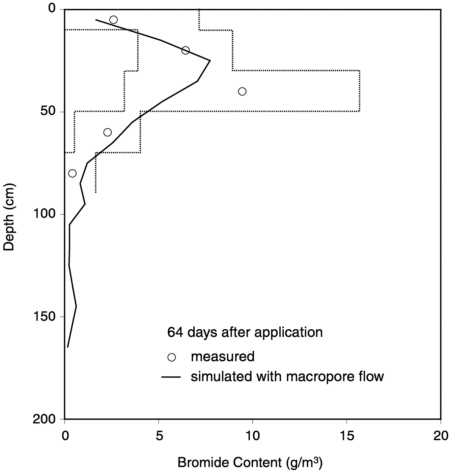
FIGURE 6-3 A comparison of bromide contents measured by soil coring at Lanna with those simulated by the MACRO model. Redrawn from Journal of Hydrology, 215, Larsson, M. H., and N. J. Jarvis, Evaluation of a dual-porosity model to predict field-scale solute transport in macroporous soil, pp. 153-171, 1999, with permission from Elsevier Science. Dotted lines indicate one standard deviation of the mean.
losses, since biodegradation in the Lanna subsoil is negligible (Bergstr öm et al., 1994). Thus, the net effect of macropore flow was a reduction of leaching of the weakly sorbed compound bentazone, by about 50 percent. However, it should be noted that significant quantities of bentazone remained in the soil at the end of the experiment, so that the net reduction in leaching due to macropore flow probably would have been smaller, had the measurements continued to the point when all the compound had been either degraded or leached.

FIGURE 6-4 A comparison of bentazone concentrations measured in tile drainage outflow at Lanna with those simulated by the MACRO model both with and without considering macropore flow. Redrawn from Journal of Hydrology, 215, Larsson, M. H., and N. J. Jarvis, Evaluation of a dual-porosity model to predict field-scale solute transport in macroporous soil, pp. 153-171, 1999, with permission from Elsevier Science.
Larsson (1999) utilized the calibrated Lanna parameter set as input to purely predictive scenario simulations investigating the interactions between pesticide compound properties and macropore flow effects on leaching. It was demonstrated that for mobile leachable compounds, macropore flow at Lanna results in small decreases in leaching, or has no effect at all, while for intermediate leachers, macropore flow may increase leaching by up to three to four orders of
magnitude. Conversely, for very strongly sorbed compounds (i.e., nonleachers), macropore flow again had apparently little effect on leaching. However, it should be borne in mind that these predictions take no account of colloid-facilitated transport of pesticide, a process that may be important for strongly sorbed compounds in macroporous soils (Brown et al., 1995). Larsson (1999) showed that to a good approximation, the total leaching loss in the presence of macropore flow
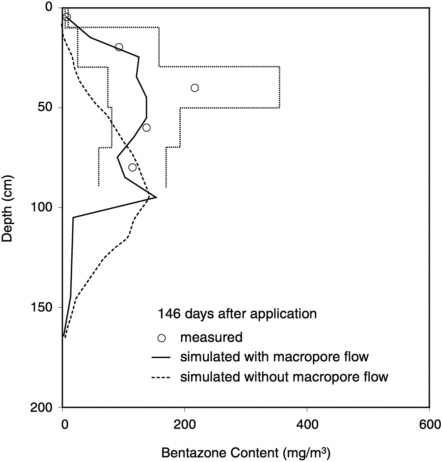
FIGURE 6-5 A comparison of bentazone contents measured by soil coring at Lanna with those simulated by the MACRO model both with and without considering macropore flow. Redrawn from Journal of Hydrology, 215, Larsson, M. H., and N. J. Jarvis, Evaluation of a dual-porosity model to predict field-scale solute transport in macroporous soil, pp. 153-171, 1999, with permission from Elsevier Science. Dotted lines indicate one standard deviation of the mean.
could be expressed as a simple linear function of the loss predicted without macropore flow, at least for compounds where leaching was more than 0.001 percent of the applied dose (see Figure 6-6). The slope of the best-fit line in Figure 6-6 reflects the tendency of macropore flow to reduce the significance of compound sorption and degradation properties in determining leaching losses. One practical consequence of this result is that reductions in applied dose would appear to be a relatively more effective means of reducing pesticide leaching in the presence of macropore flow (Larsson, 1999).
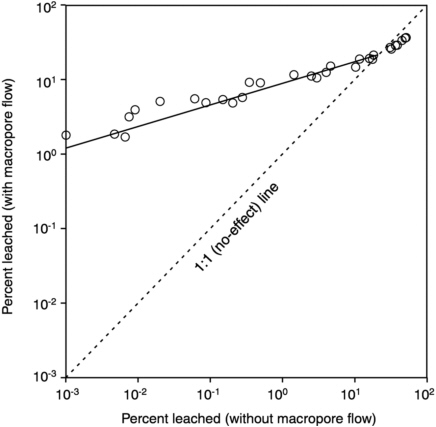
FIGURE 6-6 Leaching at Lanna (expressed as a fraction of the applied dose) for a range of hypothetical autumn-applied pesticides simulated with and without macropore flow. The one-to-one line indicates no effect of macropore flow on leaching, while the slope of the best-fit line represents the extent to which the effect of compound properties (sorption, degradation) on leaching is reduced by macropore flow. Redrawn from Larsson (1999).
The results of the scenario simulations presented by Larsson (1999) and Jarvis (1994b) can also be used to illustrate the importance of year-to-year variability in the rainfall pattern following surface application in determining leaching losses of agrochemicals in the presence of macropore flow. Figure 6-7 shows that for spring applications, annual leaching losses of bentazone predicted during a 10-year period were strongly correlated to the total rainfall in the three- to four-week period following application (Larsson, unpublished data). For less mobile pesticide compounds, the overwhelming proportion of the total leaching load during a 10-year period might be expected to occur during 1 year with heavy rainfall following spring applications (Jarvis, 1994b).
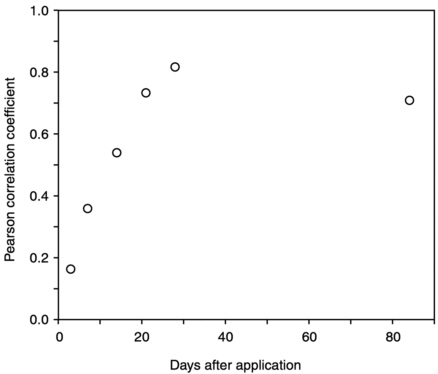
FIGURE 6-7 The relationship between predicted annual leaching loads of the spring-applied herbicide bentazone and precipitation amounts following application. The strength of the relationship is expressed in terms of the Pearson rank correlation coefficient calculated for a 10-year period.
Nitrate Leaching
Based on the calibrated parameter set derived from the model application to the bromide tracer experiment described above, Larsson and Jarvis (1999b) quantified macropore flow effects on nitrate leaching at the Lanna site by coupling MACRO to the nitrogen turnover model SOILN (Johnsson et al., 1987). The combined modeling system was applied to an eight-year field experiment carried out on an adjacent plot at Lanna, with a rotation of spring cereals and rape receiving normal rates (about 100 kg N ha−1 yr−1) of commercial fertilizer. The calibration procedure focused especially on the crop nitrogen uptake function in SOILN, in order to achieve a close match to measured nitrogen in harvested grain, which is the largest component of the mass balance of nitrogen. A comparison of model simulations (run with and without macropore flow) with measurements of mineral nitrogen in the soil profile and nitrate concentrations in tile drainage showed that (1) the model could only satisfactorily predict all measured components of the nitrogen mass balance when macropore flow was accounted for; (2) the simulation without macropore flow could be made to match measured nitrogen contents in both the soil profile and harvested grain, but nitrate concentrations in drain flow were then generally overestimated; (3) in one year, significant increases in nitrate leaching due to macropore flow were observed during a short period following spring fertilizer application; and (4) nevertheless, during the eight-year period studied, macropore flow reduced nitrate leaching at Lanna overall by about 28 percent, but with large variations occurring from year to year (reductions varied from 3 percent to 45 percent in individual years). These results clearly show that assessments of the impact of macropore flow on nitrate leaching based on short-term experiments may be misleading, especially if the experimental period immediately follows fertilizer application. For the particular soil/climate/management scenario characterized by the Lanna experiment, and for the eight-year period in question, Larsson and Jarvis (1999b) concluded that increases in leaching due to macropore flow generated by occasional periods of heavy rain following fertilizer applications in spring were clearly outweighed by reductions in leaching losses occurring during the winter periods when rainfall of low nitrogen concentrations bypasses the resident soil water with larger nitrogen concentrations.
Regulatory Use of Macropore Flow Models: Current Trends
The regulatory use of macropore flow models requires care to eliminate user bias and strict application of predefined protocols to ensure that the model is used in an appropriate manner. A transparent and uniform approach to using macropore flow models for regulatory purposes can be achieved in two possible ways. The first is the use of precalibrated scenarios, where parameter values describing soil properties, including those describing the macropore region, are fixed a priori
from previous model applications to experimental data obtained at representative sites. In this approach, the only model parameters the user is free to vary are those related to the chemical compound in question, for example, in the case of pesticides, the degradation and sorption properties and the use/application pattern. Such an approach is currently being developed for E.U. harmonized pesticide registration procedures by the FOCUS advisory group (Adriaanse et al., 1997), whereby a limited number of representative E.U. soil scenarios, for which the MACRO model has been previously calibrated, will form the basis of exposure assessments for pesticide movement to surface waters via subsurface drainage systems. Similarly, the Danish Environmental Protection Agency (DEPA) has developed two fixed national scenarios representing the main soil types in Denmark (sandy and loamy moraines). These are currently used together with the MACRO model to make pesticide exposure assessments for regulatory purposes.
Precalibrated scenarios offer a reliable means of predicting leaching with macropore flow models, but for some management applications, this approach may be too restrictive. For example, geographically distributed predictions of likely pollutant impacts on groundwater and surface waters are often required at regional and national scales. Here, macropore flow models must be used entirely predictively, with no possibility to calibrate difficult parameters. Objective and reliable estimation procedures (pedotransfer functions) are then needed to automatically derive model parameter values from widely available soils data. This approach is only likely to be possible for the simplest case of dual-porosity models, since the number of model parameters multiplies disproportionately as the number of domains increases (e.g., Gwo et al., 1995). Jarvis et al. (1997) described one such decision-support tool, or expert system (MACRO_DB, Figure 6-8), based on MACRO, in which the model is automatically parameterized from linked soils, cropping, weather, and pesticide properties databases through a combination of simple rules (based on expert judgement) and pedotransfer functions, while a geohydrological classification scheme (Boorman et al., 1991) is used to assess likely routes of pesticide contamination (surface water vs. groundwater). For example, in MACRO_DB, the diffusion pathlength is estimated from field observations of not only the size, but also the strength of development of the aggregate structure. The strength of structural development reflects the presence of cutans and organic linings at macropore/matrix interfaces, which may restrict mass exchange processes between pore domains (e.g., Thoma et al., 1992). The boundary hydraulic conductivity Kb (Figure 6-1) is one of the most sensitive hydraulic parameters in MACRO because it partitions water flow between macropores and micropores. In MACRO_DB, Kb is estimated from soil water retention curve parameters (Laliberte et al., 1968). Beulke et al. (1998) tested the predictive ability of the MACRO_DB system against a number of field and lysimeter experiments on pesticide leaching and concluded that the strength of macropore flow was significantly underestimated compared both to the measurements and to predictions made by an expert user of the stand-alone MACRO

FIGURE 6-8 Schematic diagram illustrating MACRO_DB, a decision-support tool for making pesticide exposure assessments for surface waters and groundwater. From Environmental Modelling and Software, 12, Jarvis, N. J., J. M. Hollis, P. H. Nicholls, T. Mayr, and S. P. Evans, MACRO_DB: A decision-support tool to assess the fate and mobility of pesticides in soils, pp. 251-265, 1997, with permission from Elsevier Science.
model. One reason for this may be the difficulty in estimating one critical parameter for reactive solutes, namely, the partitioning of sorption sites between the pore domains. The simple approximation currently used in MACRO_DB is to distribute the sorption sites in proportion to the relative volumes of the pore domains. In many cases, macropore interfaces and linings should be more reactive than the surface area of the bulk soil (e.g., Mallawatantri et al., 1996), but this may be more than compensated for by the much smaller surface area per soil volume (Luxmoore et al., 1990).
CONCLUDING REMARKS
Although macropore flow models are now well established as research tools, there are still few examples of management applications in the literature, and only in recent years are they starting to be used for regulatory purposes. Despite the extra difficulties of parameterizing these models, it is important that they be used for regulation, simply because the consequences of preferential flow and transport for contaminant transport are often dramatic, and because models that do not treat these processes are limited in their applicability. Thus, future regulatory use of macropore flow models is necessary, but requires strict protocols to ensure that simulations are free of subjective user bias. Regulatory applications of macropore flow models should therefore be based either on precalibrated scenarios or on objective parameter estimation routines (pedotransfer functions). In this respect, it is vital that experience in model calibration and parameterization gained in research applications is effectively made available to management users, through further development and refinement of user-friendly decision-support tools that link data sources to state-of-the-art models and parameter estimation routines. Hopefully, as research experience accumulates, macropore flow models will be increasingly used by decision-makers in risk assessments and evaluation of mitigation strategies to minimize pollution impacts on water resources.
REFERENCES
Addiscott, T.M., 1977. A simple computer model for leaching in structured soils. Journal of Soil Science 28: 554-563.
Adriaanse, P., R. Allen, V. Gouy, J. Hollis, J. Hosang, N. Jarvis, T. Jarvis, M. Klein, R. Layton, J. Linders, H. Schäfer, L. Smeets, and D. Yon, 1997. Surface water models and EU registration of plant protection products . Report 6476-VI-96 (EU Commission), Regulatory Modelling Group, FOCUS , 218 pp.
Andreu, L., F. Moreno, N. J. Jarvis, and G. Vachaud, 1994. Application of the model MACRO to water movement and salt leaching in drained and irrigated marsh soils, Marismas, Spain. Agricultural Water Management 25: 71-88.
Andreu, L., N. J. Jarvis, F. Moreno, and G. Vachaud, 1996. Simulating the impact of irrigation management on the water and salt balance in drained marsh soils (Marismas, Spain). Soil Use and Management 12: 109-116.
Armstrong, A. C., A. M. Matthews, A. M. Portwood, and N. J. Jarvis, 1995. CRACK-NP: A model to predict the movement of water and solutes from cracking clay soils. ADAS Report, Land Research Centre, Gleadthorpe, Mansfield, Notts. , U.K., 63 pp.
Armstrong, A. C., A. M. Portwood, P. B. Leeds-Harrison, G. L. Harris, and J. A. Catt, 1996. The validation of pesticide leaching models. Pesticide Science 48: 47-55.
Barraclough, D., 1989a. A useable mechanistic model of nitrate leaching. I. The model. Journal of Soil Science 40: 543-554.
Barraclough, D., 1989b. A useable mechanistic model of nitrate leaching. II. Application. Journal of Soil Science 40: 555-562.
Bergström, L., N. J. Jarvis, and J. Stenström, 1994. Pesticide leaching data to validate simulation models for registration purposes. Journal of Environmental Science and Health A29(6): 1073-1104.
Bergström, L., 1996. Model predictions and field measurements of Chlorsulfuron leaching under non-steady-state flow conditions. Pesticide Science 48: 37-45.
Beulke, S., C. D. Brown, and I. Dubus, 1998. Evaluation of the use of preferential flow models to predict the movement of pesticides to water sources under UK conditions. Final Report on MAFF project PL0516 SSLRC, Cranfield University, Silsoe, U.K.
Besien, T. J., N. J. Jarvis, and R. J. Williams, 1997. Simulation of water movement and isoproturon behaviour in a heavy clay soil using the MACRO model. Hydrology and Earth System Sciences 1: 835-844.
Beven, K., and P. Germann, 1982. Macropores and water flow in soils. Water Resources Research 18: 1311-1325.
Booltink, H.W.G., R. Hatano, and J. Bouma, 1993. Measurement and simulation of bypass flow in a structured clay soil: A physico-morphological approach. Journal of Hydrology 148: 149-168.
Boorman, D. B., J. M. Hollis, and A. Lilly, 1991. The production of the hydrology of soil types (HOST) data set. In: British Hydrological Society, 3rd National Hydrology Symposium, Southampton, U.K., pp. 6.7-6.13.
Bourgault de Coudray, P. L., D. R. Williamson, and W. D. Scott, 1997. Prediction of chloride leaching from a non-irrigated, de-watered saline soil using the MACRO model. Hydrology and Earth System Sciences 1: 845-851.
Brooks, R. H., and A. T. Corey, 1964. Hydraulic properties of porous media. Hydrology Paper no. 3, Colorado State University, Ft. Collins, Colo., 27 p.
Brown, C. D., R. A. Hodgkinson, D. A. Rose, J. K. Syers, and S. J. Wilcockson, 1995. Movement of pesticides to surface waters from a heavy clay soil. Pesticide Science 43: 131-140.
Clothier, B. E., and K. R. J. Smettem, 1990. Combining laboratory and field measurements to define the hydraulic properties of soil. Soil Science Society of America Journal 54: 299-304.
Corwin, D. L., B. L. Waggoner, and J. D. Rhoades, 1991. A functional model of solute transport that accounts for bypass. Journal of Environmental Quality 20: 647-658.
Durner, W., 1992. Predicting the unsaturated hydraulic conductivity using multi-porosity water retention curves. In: Proc. of the International Workshop, Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils (M. Th. van Genuchten, F. Leij, and L. Lund, eds.), University of California, Riverside, pp. 185-201.
Flühler, H., W. Durner, and M. Flury, 1996. Lateral solute mixing processes: A key for understanding field-scale transport of water and solutes. Geoderma 70: 165-183.
Gamerdinger, A. P., R. J. Wagenet, and M. Th. van Genuchten, 1990. Application of two-site/two-region models for studying simultaneous nonequilibrium transport and degradation of pesticides. Soil Science Society of America Journal 54: 957-963.
Gerke, H. H., and M. Th. van Genuchten, 1993a. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resources Research 29: 305-319.
Gerke, H. H., and M. Th. van Genuchten, 1993b. Evaluation of a first-order water transfer term for variably saturated dual-porosity flow models. Water Resources Research 29: 1225-1238.
Germann, P., 1985. Kinematic wave approach to infiltration and drainage into and from soil macropores. Trans. ASAE 28: 745-749.
Gottesbüren, B., W. Mittelstaedt, and F. Führ, 1995. Comparison of different models to simulate the leaching behaviour of quinmerac predictively. In: Proceedings of the BCPC Symposium Pesticide Movement to Water (A. Walker, R. Allen, S. W. Bailey, A. M. Blair, C. D. Brown, P. Günther, C. R. Leake, and P. H. Nicholls, eds.), Warwick, U.K., pp. 155-160.
Gwo, J. P., P. M. Jardine, G. V. Wilson, and G. T. Yeh, 1995. A multiple-pore-region concept to modeling mass transfer in subsurface media. Journal of Hydrology 164: 217-237.
Hall, D. G. M., 1993. An amended functional leaching model applicable to structured soils . Journal of Soil Science 44: 579-588.
Hillel, D., 1987. Unsflow in layered soils: A review. Hydrological Processes 1: 143-147.
Hutson, J. L., and R. J. Wagenet, 1995. A multiregion model describing water flow and solute transport in heterogeneous soils. Soil Science Society America Journal 59: 743-751.
Jarvis, N. J., 1989. CRACK: A model of water and solute movement in cracking clay soils . Technical description and user notes. Report 159, Division of Agricultural Hydrotechnics, Department of Soil Sciences, Swedish University of Agricultural Sciences , Uppsala, 38 pp.
Jarvis, N. J., 1994a. The MACRO model (Version 3.1): Technical description and sample simulations . Reports and Dissertations, 19, Department of Soil Sciences, Swedish University of Agricultural Sciences , Uppsala, 51 pp.
Jarvis, N. J., 1994b. The implications of preferential flow for the use of simulation models in the registration process. In: Proceedings of the 5th International Workshop Environmental Behaviour of Pesticides and Regulatory Aspects (COST) (A. Copin, G. Houins, L. Pussemier, J. F. Salembier, eds.), Brussels, April, pp. 464-469.
Jarvis, N. J., M. Stähli, L. Bergström, and H. Johnsson, 1994. Simulation of dichlorprop and bentazon leaching in soils of contrasting texture using the MACRO model. Journal of Environmental Science and Health A29(6): 1255-1277.
Jarvis, N. J., 1995. Simulation of soil water dynamics and herbicide persistence in a silt loam soil using the MACRO model. Ecological Modeling 81: 97-109.
Jarvis, N. J., and I. Messing, 1995. Near-saturated hydraulic conductivity in soils of contrasting texture as measured by tension infiltrometers. Soil Science Society of America Journal 59: 27-34.
Jarvis, N. J., M. Larsson, P. Fogg, and A. D. Carter, 1995. Validation of the dual-porosity model MACRO for assessing pesticide fate and mobility in soil. In: Proc. BCPC Symposium Pesticide Movement to Water (A. Walker, R. Allen, S. W. Bailey, A. M. Blair, C. D. Brown, P. Günther, C. R. Leake, and P.H. Nicholls, eds.), Warwick, U.K., pp. 161-170.
Jarvis, N. J., J. M. Hollis, P. H. Nicholls, T. Mayr, and S. P. Evans, 1997. MACRO_DB: A decisionsupport tool to assess the fate and mobility of pesticides in soils. Environmental Modelling and Software 12: 251 - 265.
Jarvis, N. J., 1998. Modeling the impact of preferential flow on nonpoint source pollution . In: Physical Non-Equilibrium in Soil: Modeling and Application (H. M. Selim and L. Ma, eds.), pp. 195-221. Ann Arbor Press.
Jarvis, N. J., and M. H. Larsson, 1998. The MACRO model (Version 4.1): Technical description. http://130.238.110.134:80/bgf/Macrohtm/macro.htm. Department of Soil Sciences, Swedish University of Agricultural Sciences , Uppsala.
Jarvis, N. J., I. Messing, M. H. Larsson, and L. Zavattaro, 1999. Measurement and prediction of near-saturated hydraulic conductivity for use in dual-porosity models. In: Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media (M. Th. van Genuchten, F. Leij, and L. Wu, eds.). University of California, Riverside, pp. 839-850.
Jarvis, N. J., C. D. Brown, and E. Granitza, 2000. Sources of error in model predictions of pesticide leaching: A case study using the MACRO model. Agricultural Water Management 44: 247-262.
Johnsson, H., L. Bergström, P.-E. Jansson, and K. Paustian, 1987. Simulated nitrogen dynamics and losses in a layered agricultural soil. Agriculture, Ecosystems and Environment 18: 333-356.
Jørgensen, P. R., T. Schrøder, G. Felding, A. Helweg, N.-H. Spliid, M. Thorsen, J.-C. Refsgaard, and O.-H. Jacobsen, 1998. Validation and development of pesticide leaching models. Pesticides Research no. 47, Danish Environmental Protection Agency, Copenhagen, 150 pp.
Lafolie, F., and Ch. Hayot, 1993. One-dimensional solute transport modelling in aggregated porous media . Part 1. Model description and numerical solution. Journal of Hydrology 143: 63-83.
Laliberte, G. E., R. H. Brooks, and A. T. Corey, 1968. Permeability calculated from desaturation data. J. Irrig. and Drainage Div., Proc. ASCE, 94: 57-69.
Larsson, M. H., and N. J. Jarvis, 1999a. Evaluation of a dual-porosity model to predict field-scale solute transport in macroporous soil. Journal of Hydrology 215: 153-171.
Larsson, M. H., and N. J. Jarvis, 1999b. A dual-porosity model to quantify macropore flow effects on nitrate leaching. Journal of Environmental Quality 28: 1298-1307.
Larsson, M. H., 1999. Quantifying macropore flow effects on nitrate and pesticide leaching in a structured clay soil: Field experiments and modelling with the MACRO and SOILN models. Acta Universitatis Agriculturae Sueciae, Agraria 164, SLU, Uppsala, Sweden, 34 pp.
Loague, K. M., and R. E. Green, 1991. Statistical and graphical methods for evaluating solute transport models: Overview and application. Journal of Contaminant Hydrology 7: 51-73.
Luxmoore, R. J., P. M. Jardine, G. V. Wilson, J. R. Jones, and L. W. Zelazny, 1990. Physical and chemical controls of preferred path flow through a forested hillslope. Geoderma 46: 139-154.
Mallawatantri, A. P., B. G. McConkey, and D. J. Mulla, 1996. Characterization of pesticide sorption and degradation in macropore linings and soil horizons of Thatuna silt loam. Journal of Environmental Quality 25: 227-235.
Mualem, Y., 1976. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research 12: 513-522.
Nicholls, P. H., and D. G. M. Hall, 1995. Use of the pesticide leaching model (PLM) to simulate pesticide movement through macroporous soils. In Proc. BCPC Symposium Pesticide Movement to Water (A. Walker, R. Allen, S. W. Bailey, A. M. Blair, C. D. Brown, P. Günther, C. R. Leake, and P. H. Nicholls, eds.), Warwick, U.K., pp. 187-192.
Nieber, J. L., and D. Misra, 1995. Modeling flow and transport in heterogeneous, dual-porosity drained soils. Irrigation and Drainage Systems 9: 217-237.
Oreskes, N., K. Schrader-Frechette, and K. Belitz, 1994. Verification, validation and confirmation of numerical models in the earth sciences. Science 263: 641-646.
Othmer, H., B. Diekkrüger, and M. Kutilek, 1991. Bimodal porosity and unsaturated hydraulic conductivity. Soil Science 152: 139-150.
Russell, M. H., R. J. Layton, and P. M. Tillotson, 1994. The use of pesticide leaching models in a regulatory setting: an industrial perspective. Journal of Environmental Science and Health A29: 1105-1116.
Rykiel, E. J., 1996. Testing ecological models: The meaning of validation. Ecological Modelling 90: 229-244.
Saxena, R., N. J. Jarvis, and L. Bergström, 1994. Interpreting non-steady state tracer breakthrough experiments in sand and clay soils using a dual-porosity model. Journal of Hydrology 162: 279-298.
Smettem, K. R. J., and C. Kirkby, 1990. Measuring the hydraulic properties of a stable aggregated soil. Journal of Hydrology 117: 1-13.
Steefel, C. I., and P. van Cappellen, 1998. Reactive transport modeling of natural systems. Journal of Hydrology 209: 1-7.
Steenhuis, T. S., J.-Y. Parlange, and M. S. Andreini, 1990. A numerical model for preferential solute movement in structured soils. Geoderma 46: 193-208.
Thoma, S. G., D. P. Gallegos, and D. M. Smith, 1992. Impact of fracture coatings on fracture/matrix flow interactions in unsaturated, porous media. Water Resources Research 28: 1357-1367.
van Dam, J.C., J. M. H. Hendrickx, H. C. van Ommen, M. H. Bannink, M. Th. van Genuchten, and L. W. Dekker, 1990. Water and solute movement in a coarse-textured water-repellent field soil. Journal of Hydrology 120: 359-379.
van Genuchten, M. Th., and P. J. Wierenga, 1976. Mass transfer in sorbing porous media. I. Analytical solutions. Soil Science Society of America Journal 40: 473-480.
van Genuchten, M. Th., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal 44: 892-898.
van Genuchten, M. Th., 1985. A general approach for modeling solute transport in structured soils . In: Proceedings of the 17th International Congress IAH, Hydrogeology of Rocks of Low Permeability. Memoires IAH, 17, pp. 513-526.
van Genuchten, M. Th., and R. J. Wagenet, 1989. Two-site/two-region models for pesticide transport and degradation: Theoretical development and analytical solutions. Soil Science Society of America Journal 53: 1303-1310.
Villholth, K. G., and K. H. Jensen, 1998. Flow and transport processes in a macroporous subsurfacedrained glacial till soil. II. Model analysis. Journal of Hydrology 207: 121-135.
Wagenet, R. J., and J. L. Hutson, 1987. LEACHM: Leaching estimation and chemistry model. A process-based model of water and solute movement, transformations, plant uptake and chemical reactions in the unsaturated zone. Continuum 2, Water Resources Institute, Cornell University, Ithaca, N.Y.
Wauchope, R. D., 1992. Environmental risk assessment of pesticides: Improving simulation model credibility. Weed Technology 6: 753-759.
Youngs, E. G., and P. B. Leeds-Harrison, 1990. Aspects of transport processes in aggregated soils. Journal of Soil Science 41: 665-675.
Zurmühl, T., and W. Durner, 1996. Modeling transient water and solute transport in a biporous soil. Water Resources Research 32: 819-829.




























