Appendix E
Glossary of Terms
UNDERWATER ACOUSTICS TERMS
This glossary contains definitions and explanations for many of the terms used in this report. Most of these definitions are consistent with those in the American National Standards Institute’s (1994) “Acoustical Terminology” and those in Harris (1991). The text below indicates where the definitions in this report differ somewhat from the standard definitions. The first part of this glossary is divided into the following sections in order to group together concepts on a similar topic: “Noise and Statistical Analysis,” “Physics of Sound,” “Spectral Analysis and the Frequency Domain,” “Temporal Character of Man-made Sounds,” and “A Few Specific Sources of Noise.”
Decibel—a logarithmic measure of the relative amplitude of two quantities. The two quantities being compared must have the same units so that their ratio is unitless. In underwater acoustics, the standard unit of acoustic pressure is the micro Pascal (µPa), or one-millionth of a Pascal. Therefore, the amplitude of acoustic pressure is compared to 1 µPa so that the sound pressure level (SPL) is defined as
SPL = 20*log10(Ap/1 µPa)
where Ap is the pressure amplitude determined in a specified way (e.g., peak amplitude, RMS amplitude). The units of SPL are dB re 1 µPa. An equivalent way of defining the SPL is in terms of the square of the pressure amplitude,
SPL = 10*log10(Ap*Ap/(1 µPa)2)
The deci in decibel indicates that the logarithm to the base 10 of squared pressure is multiplied by a factor of 10. This factor of 10 applies to quantities that are second order in the acoustic variables; for example, are proportional to the square of pressure, squared particle velocity amplitude, or the product of pressure and particle velocity. Examples of such quantities are acoustic energy density, magnitude of vector acoustic intensity, and acoustic power (see the “Physics of Sound” section of the Glossary). A factor of 20 is used for quantities at first order in the acoustic variables– acoustic pressure and acoustic particle velocity amplitude, for example. With regard to particle velocity, the sound particle velocity amplitude level (SPVL) can be defined in terms of the particle velocity amplitude, Av, as
SPVL = 20*log10(Av/1 m/s) = 10*log10[Av*Av/(1 m/s)2]
It has units of dB re 1 m/s. More care must be taken in dealing with particle velocity because of its vector nature and because the polarization of the motion typically is more complicated than that of simple rectilinear motion.
The original definition of the decibel was given in terms of intensity amplitude ratios. This original definition is repeated in some modern textbooks. However, as indicated above, the decibel now is used in a much broader way, as can be seen in the national and international acoustics standards adopted by the American National Standards Institute (ANSI) and the International Organization for Standardization (ISO). In fact, those textbooks that define the decibel in terms of intensity amplitude ratios often proceed to report quantities in units of dB re 1 µPa or dB re 1 µPa2; these reference values pertain to quantities of pressure and pressure squared, respectively, and are not the units of intensity amplitude (which are W/m2).
Calls for the elimination of the decibel sometimes are heard. The decibel is here to stay, not only because it is part of ANSI and ISO standards, but because it is a valuable way (among others) of reporting acoustical quantities. It was invented and popularized for good reasons by the early pioneers in acoustics. The major reasons for its continued usefulness are given in Chapter 1, such as the fact that sound levels can span a large range of values (large dynamic range) and human perception of loudness appears to be logarithmic in nature. A far better recommendation than the elimination of the decibel is to insist that its reference units always be reported clearly.
Acoustic Source Properties, Sound Field Properties, and Properties of the Fluid Medium
Quantities that measure properties of the sound field and those that measure properties of the fluid medium itself must be clearly distinguished. For example, specific acoustic impedance is a property of a received sound field, whereas characteristic acoustic impedance is a property of the medium (see the “Physics of Sound” section of the Glossary). Another example is sound speed; group speed and phase speed are properties of a sound field, whereas medium sound speed obviously is a property of the medium. Acoustic density is the perturbation of the fluid density from its ambient value by the presence of sound and so is a property of the sound field. In contrast, the fluid ambient density is the density of the medium in the absence of sound. The same relationship holds for acoustic pressure and hydrostatic pressure.
Likewise, clear distinctions must be made between the properties of an acoustic source and those of a received field. For example, the sound level at a receiver is reduced from the source level by the transmission loss between source and receiver. (This transmission loss is quite large over short distances at close range from point-like sources as a result of spherical spreading.) The character of a received signal is due not only to the source of the signal but also the medium through which the signal has traveled. The received level is directly measured, whereas source level must be derived for many types of sources. For controlled, man-made sources that intentionally transmit sound such as sonars and air-gun arrays, the source level in most cases is well known. However, to derive the source level for uncontrolled and naturally occurring sources using underwater acoustic measurements of the received field, the location of the source must be known or determined, and the propagation conditions from source to receiver location must be accurately modeled. This effort has been accomplished successfully in situations for naturally occurring discrete sources that can be modeled as simple points in space such as individual vocalizing animals. However, estimating the source levels of spatially diffuse naturally occurring sources—chorusing fish schools, snapping shrimp colonies, ocean surface breaking waves, oscillating bubble clouds—is a topic of research. In other cases, the propagation conditions from source to receiver are too complicated to model with reliable accuracy at present and are areas of modern-day research. Examples of such naturally occurring sources in this category are earthquakes, surf, and lightning.
Noise and Statistical Analysis
Ambient Noise—the noise associated with the background din emanating from a myriad of unidentified sources. Its distinguishing features are that it
is due to multiple sources, individual sources are not identified (although the type of noise source—e.g., shipping, wind—may be known), and no one source dominates the received field. Ambient noise is not necessarily that from distant sources, as sometime stated, since the collection of breaking waves directly above a receiver are not “distant” nor is thermal agitation. In addition, ambient noise in this report does not imply naturally occurring since ocean traffic noise has long been considered part of the ambient. Finally, although ambient noise is continuously present (at varying levels), the individual sources contributing to this background din do not have to create sounds continuously in time. The collection of individual snapping sounds from a colony of snapping shrimp, the clicking from a pod of sperm whales, or the sounds of breaking waves from a surface distribution of whitecaps typically are considered contributors to the ambient field even though the individual signals are transient in time.
Ambient vs. Specific Sources, Stochastic (Random) vs. Deterministic—the distinction between what is part of the ambient noise field and what is considered to originate from specific sources is somewhat arbitrary. For example, distant ships that contribute to the ambient noise field can become part of the set of specific sources with additional information. However, in any measurement or modeling effort, perfect knowledge of the contributing sources, their source characteristics, or the environment can never be achieved. The distinction between ambient noise and that from specific sources has a direct impact on modeling and the interpretation of signal processing results. Since ambient indicates a collection of sources not specifically identified, this component is modeled as stochastic in nature. That is, the properties of an ensemble (or collection) are the relevant features; for example, the probability of getting a 6 on the roll of a die. On the other hand, sounds from an identified source typically are modeled deterministically—the properties of a given realization are relevant. For example, a deterministic approach to rolling a die would predict what face of the die will appear given the die’s initial position and velocity, its elastic properties and those of the table on which it lands.
The proper interpretation of data analysis results also requires an understanding of the distinction between stochastic and deterministic processes. For example, the spectral density of a continuous-in-time, aperiodic, deterministic signal is interpreted as the signal’s mean squared amplitude per frequency, whereas for a stochastic signal it is the variance of the signal on a per frequency basis.
Noisy, Loud—describe the perception of sound and are not a property of the sound field itself. Their proper interpretation requires a clear indication of the perceiver of the sound; loud to whom, noisy to what species of
marine mammal, and so on. Note that nowhere in this report is a comparison presented of the sound levels of various airborne sources and underwater acoustic sources. Such a comparison tends to anthropomorphize the effects of underwater noise sources. The issue here is not whether a given ocean acoustic source is “as loud as a jet engine” to a human, but rather how loud it is to a given marine species underwater. (The committee did not deal with the issue of the impact of airborne sound on marine mammals in air, only on the potential impact of airborne sound once it coupled into the underwater acoustic field.) Sounds that humans find bothersome may not have a significant impact on some marine species; conversely, sounds we cannot perceive may have significant adverse impact on some species in the marine environment.
Ocean Noise—the underwater sound from all types of noise sources, including noise from specific identified sources as well as ambient noise. For the purposes of evaluating the potential effects of underwater sound on the marine environment, both ambient noise and the noise from identified sources must be considered.
Variance—a statistical quantity that measures the variation (spread) of a random variable about its average (mean) value. For example, if the individual acoustic pressure samples as a function of time are assumed to be realizations of an underlying random process, the mean squared pressure is an estimate of the variance of the random process. The mean (a statistical measure of central tendency) of acoustic pressure and of acoustic particle velocity is equal to zero, by their definitions as variations about an equilibrium state. For stochastic (random) processes, the spectrum is the variance as a function of frequency. Likewise, the spectral density is the variance on a per frequency basis (Bendat and Piersol, 1986), and integration across all frequencies is equal to the broadband spectral level and to the variance of the original time series.
Other statistical properties of the ambient noise field are studied, such as its temporal and spatial coherence (measures of the degree of relatedness of two signals separated in time and in space, respectively; for example, see references in Urick, 1984) because of their relevance to signal and array processing and because they help identify certain noise source and propagation properties. A closely related property to spatial coherence is the directionality of the field, both vertically and azimuthally. The field’s directional properties may be quite relevant to its potential impact on marine mammal hearing. For example, a diffuse interfering sound field may have a greater impact on masking than a highly directional one.
Physics of Sound
The field of physics contains words that also are used in common, everyday language. Examples are intensity, power, work, and energy. In physics these words have very specific and well-established definitions. However, they are often misused in the underwater acoustics literature. The most prevalent error probably is the use of intensity to describe the mean square pressure. Another common mistake is to use power when referring to instantaneous squared pressure and to refer to the sum of squared pressure over time as energy. The descriptions below conform to the physics definition of the terms as they apply to the study of acoustics. They are presented in this report to help remove the confusion that surrounds this topic.
Acoustic Energy Density—the energy per unit volume in the sound field. Two types of mechanical energy density exist in an acoustic field, potential energy density and kinetic energy density. The potential energy density measures the ability of the deformed fluid (deformed by the presence of sound) to do work. The acoustic kinetic energy density measures the ability of the fluid to do work because of the fluid motion associated with the acoustic field. The mean square pressure is proportional to the average potential energy density. Therefore, the integral of the pressure squared over a time interval is simply the mean squared pressure multiplied by the duration of the time interval, or proportional to the average potential energy density multiplied by the duration of the time interval. This time integral is not equal to energy, as it is sometimes mistakenly called. Similarly, the acoustic kinetic energy density is proportional to the mean squared particle velocity amplitude. The standard units of energy are joules, so that acoustic energy density (either potential or kinetic, or the sum of the two) has decibel units of dB re 1 J/m3. Both types of acoustic energy density and acoustic energy (obtained by summing the energy densities over a specified volume of fluid) are second order in acoustic field variables.
Acoustic Impedance—a measure of the resistance to acoustic motion. There are two types of impedance that measure significantly different properties. Characteristic impedance is a property of the fluid medium itself and is equal to the product of the fluid ambient density (mass per unit volume in the absence of sound) and the speed of sound. The second type is specific acoustic impedance. It is a property of the sound field at a given point in space and is equal to the ratio of the acoustic pressure amplitude to acoustic velocity amplitude. As in the discussion of the decibel, the particle motion in acoustic fields can be quite complicated so that care is required in dealing with specific acoustic impedance. For example, acoustic velocity at a given frequency can have a component that is in quadrature with the acoustic pressure as well as one in phase, so that the specific acoustic impedance can
have both real and imaginary components. In a few special sound fields, such as a single plane wave in a homogeneous fluid, the specific acoustic impedance equals the characteristic impedance. However, this equivalence does not hold in general.
Acoustic Intensity—the flow of acoustic energy through a surface with unit area per unit time. It is equivalent to acoustic energy flux density. Acoustic intensity equals the product of the acoustic pressure with the acoustic particle velocity, and therefore it is second order in acoustic field variables. As with particle velocity, acoustic intensity is a vector quantity; it has both a magnitude and a direction. The direction is the direction of flow of acoustic energy and is perpendicular to the surface with unit area referred to in the first line of this definition. The magnitude of the time-averaged flux density is not proportional to the mean squared acoustic pressure except in a few special types of sound fields. Energy flux density in acoustic fields can be categorized into two types. The first type, called active intensity, is the net flux of energy. It measures the propagating part of the sound field, which is that part of the field that can transfer information from one location to another. The second type of energy flux density has a time average of zero. However, this flow, the reactive intensity, is equally important in that it allows interference patterns in acoustic fields to exist. The units of acoustic intensity are those of energy per unit time per unit area. The standard units of energy are joules. A joule per second is equal to one watt. Therefore, acoustic intensity has units of W/m2. In those rare cases in the underwater acoustics literature where true vector acoustic intensity is discussed, the reference unit of intensity typically is 1 pW/m2 so that the corresponding decibel units are dB re 1 pW/m2.
Acoustic Particle Velocity—the velocity of the fluid itself associated with the presence of a sound field. Velocity has both a magnitude and a direction (i.e., it is a vector quantity); pressure has magnitude only (it is a scalar quantity). The units of particle velocity amplitude in the SI system of units are m/s. A common assumption is that the acoustic particle velocity is “rectilinear”; that is, the particle motion is back and forth along a linear path along the direction of propagation. This type of motion occurs only in specific wave fields, such as a single propagating plane wave in a whole space or at specific points in space in more general types of wave fields. In ocean acoustic propagation, the particle can be elliptical or circular, both in the prograde and retrograde directions, as well as rectilinear. Acoustic particle velocity, along with acoustic pressure is a quantity that is first order in the acoustic field variables.
Acoustic Power—the integral over a well-defined surface area of the component of active vector acoustic intensity perpendicular to the surface.
Since the value of power will depend upon the area and orientation of the surface, as well as its location in the medium, the characteristics of the surface over which the integration is performed must be clearly specified. An important exception occurs when the area is that of a simple closed surface, such as a sphere. If the region enclosed by this simple closed surface does not include an acoustic source, the time-averaged acoustic power equals zero. That is, as much acoustic energy flows into the sphere as out of it, on average. This result is true for other simple closed surface shapes such as a cube or cylinder. If a source of sound is contained within the closed surface, the acoustic power measured by integrating the intensity over the surface is equal to the acoustic power of the source itself, regardless of the dimensions of the enclosing region (assuming that absorption of sound within the enclosed region is negligible). Therefore, for simple closed surfaces, acoustic power is a property of the source(s) contained within the region and is not a property of the sound field itself. Power is the time rate of change of energy in a system, so that the acoustic power of a source is the rate at which the source puts acoustic energy into the fluid medium. The units of acoustic power are joules per second, or watts, so that its decibel units are dB re 1 pW. As an example, a 75-watt lightbulb consumes nearly 139 dB re 1 pW of electrical power. Power, like intensity, is second order in acoustic field variables.
Acoustic Pressure—the force per unit area exerted by the fluid due as a result of its deformed state in a sound field. This force per unit area is analogous to the force exerted by a stretched or compressed spring. Acoustic pressure variations are variations of fluid pressure about an equilibrium value. In underwater acoustics, the equilibrium pressure is determined by the weight of the overlying water column (in atmospheric acoustics it is the weight of the overlying column of air) in the earth’s gravitational field. The units of pressure in the SI system of units are pascals (Pa). In underwater acoustics the standard reference is one-millionth of a Pascal, called a micropascal (1 µPa). Acoustic pressure, like acoustic particle velocity, is first order in the acoustic field variables. The other acoustic field quantities presented in this section—acoustic energy density, acoustic intensity, and acoustic power—are second-order field quantities.
Adiabatic Incompressibility—the change in pressure (acoustic pressure plus ambient pressure) required to cause a unit fractional change in the fluid density. It measures how much force is needed to cause a given change in fluid volume. The adiabatic part of the term signifies that during the change in pressure, no heat or other form of energy is able to enter or escape the fluid undergoing deformation. Every type of wave motion requires some kind of force that tends to restore equilibrium conditions. In acoustics this restoring force is provided by the “springiness” of the fluid.
The adiabatic incompressibility, also called the bulk modulus, is the quantitative measure of the “stiffness” of the springiness of a fluid. It is derived by the fluid ambient density multiplied by the square of the medium sound speed.
Fluid Ambient Density—a property of a fluid that is equal to its mass per unit volume in the absence of sound. The term ambient as used here signifies the fluid’s equilibrium state and should be distinguished from its use in the term ambient noise.
Shock Wave—an acoustic wave where the amplitude of the field is so large that the linear approximation to the governing physics equations is no longer valid and where discontinuities in acoustic quantities such as pressure and particle velocity can occur.
Sound—mechanical waves in a fluid that cause fluid motion and changes in pressure—compressions and dilatations—about an equilibrium state. The deformations in an individual freely propagating plane wave have a specific relationship between the temporal and spatial scales of variation in the direction of propagation. This relationship is given by the speed of sound. In addition, sound waves usually travel through a fluid medium without resulting in a net transport of the fluid itself—an exception occurs when the amplitude of the field becomes so large that nonlinear terms in the governing equations become important, as in a shock wave. The basic physics of sound is based on fundamental conservation laws (conservation of mass, conservation of momentum, and conservation of energy). A commonly held view of acoustics is, “I know sound when I hear it.” However, this statement is not true, for example, when the wind is “heard” blowing past one’s ears as a result of the pressure fluctuations associated with wind turbulence. It is important to distinguish between the physical properties of sound itself and the perception of sound by humans and animals.
Spectral Analysis and the Frequency Domain
Note that some of the terms below (spectrum and spectral density) are defined in a somewhat different way than is found in textbooks.
Autospectrum, Autospectral Density —see Spectrum; see Spectral Density
Fast Fourier Transform (FFT)—a computationally efficient algorithm for performing the Fourier transform with digitized data. The FFT can be viewed as a bank of narrow bandpass filters adjacent in frequency. The output of each filter is the equivalent amplitude and phase of the narrow band of frequency components centered on that filter’s center frequency
that are contained in the time series. Computer codes that implement the fast Fourier transform are readily available. Window functions often are used to taper the ends of a segment of time series prior to performing the transform in order to reduce the possibility of the spectral levels in one frequency band contaminating the levels in a significantly different frequency band (“spectral leakage”; resulting from the spectral sidelobes of the window function; see Harris, 1978). In order to numerically calibrate the FFT output to obtain an auto spectrum or autospectral density, the square of the Fourier transform amplitudes is normalized by the following quantities:
Autospectrum: square of the sum of the window values over the FFT length (fftl):
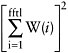
Autospectral Density: sum of the squared individual window values times the data sampling frequency (fs):
If a rectangular window is used so that W(i) = 1/fftl for all i = 1 to fftl, the normalization factor for the autospectrum is equal to one, and that for the autospectral density equals fs/fftl, which equals the FFT frequency resolution (bin width). These normalization factors pertain to “two-sided” autospectra and autospectral densities (i.e., those with both positive and negative frequencies); for one-sided quantities that span only the nonnegative frequencies, the normalization factors are half those given above (Bendat and Piersol, 1986).
Fourier Transform—a mathematical transformation that converts data values as a function of time (time series) into values as a function of frequency. In effect, the Fourier transform of a recorded piece of music describes the frequencies and levels of the individual notes (and their phases) that were played in creating the music. The transform is linear in the sense that the Fourier transform of a sum of quantities is equal to the sum of their transforms. The original time series can be reconstructed exactly from the Fourier transform output by an inverse transform. For this reason, a signal in the time domain and its corresponding Fourier transform in the frequency domain are considered transform pairs. An analogous relationship
exists between the space and spatial frequency domains. (The inverse of the spatial frequency in a given spatial dimension is proportional to the wavelength of the wavefield in that dimension, just as the inverse of temporal frequency is proportional to the period of the wavefield.)
There exist several theorems that relate the properties of signals in the time domain and their corresponding Fourier transforms. These theorems can have important applications to the topic of this report. As a possible example, consider the rise time of an acoustic signal, which may be an important metric for evaluating the potential impact of a given sound on marine animals. A related concept is the rate of change of the signal amplitude with time, given by its derivative with time. A theorem in Fourier analysis states that the transform amplitude of the derivative of a signal is proportional to frequency multiplied by the transform amplitude of the original signal. Therefore, the higher-frequency components of a signal have greater importance in determining its time rate of change than the lower-frequency components (and must be present for a rapid rise time to occur). This theorem allows the Fourier transform and spectrum of the time rate of change of a quantity to be determined directly from the Fourier transform of the quantity itself.
Frequency—rate at which a repetitive event occurs, measured in hertz (Hz), cycles per second (from Richardson et al., 1995).
Infrasonic—describing sound that is lower in frequency than the minimum audible to humans generally below 20 Hz. Some baleen whales produce infrasonic sound.
Octave—a continuous band of frequencies in which the highest frequency is twice that of the lowest frequency.
Octave Band Levels—the spectral level obtained by integrating the spectral density across the octave band of interest.
One-third-Octave and One-third-Octave Band Levels—a third of an octave is a continuous band of frequencies in which the highest frequency is the cube root of 2 (21/3) times that of the lowest frequency. A one-third-octave band about a center frequency of Fc ranges from Fc/(21/6) to Fc*(21/6). The nominal standard bandwidth for the way in which the mammalian ear processes sound is a third octave. A one-third-octave band level is the spectral level obtained by integrating the spectral density across the one-third-octave band of interest.
Spectral Density (Spectral Density Function)—the spectrum per unit frequency. It is defined mathematically in terms of a limit, but numerical
estimates are based on normalizing by the FFT binwidth. The autospectral density is the spectral density for a single time series of a specified quantity (versus the cross-spectral density, involving two different time series, which is not discussed in this report). The spectral density is the most appropriate quantity to use with signals whose spectral content varies continuously with frequency in a relatively smooth way (“continuous spectra”; see Priestley, 1989) since the numerical estimates of the spectral density levels of very narrow band components (lines) are dependent upon the FFT length. The spectrum level in a given frequency band (the “band spectral level”) can be obtained by integrating the spectral density across that band. Because of the overall increase in ocean ambient noise levels with decreasing frequency, band spectral levels are particularly sensitive to the lower frequency limit of the integration. The mean squared amplitude (or variance for random processes) of the original time series over a given time interval equals the integral of the spectral density for that time period across the whole frequency band. The decibel unit for the pressure spectral density in underwater acoustics is dB re 1 µPa2/Hz and those for the particle velocity spectral density are dB re 1 (m/s)2/Hz.
Spectral Level and Spectral Density Level—As used in this report, spectral level refers to either the band spectral level across a specified frequency band or the spectral level at a given frequency for narrowband tones, and spectral density level is the level of the spectral density. The two are not synonymous, in contrast to the definition in ANSI (1994).
Spectrum—in general, the frequency (temporal or spatial) dependence of some quantity. In this report, the spectrum of acoustic field quantities also is used for the band spectrum (across a specified frequency band) for continuous-in-frequency spectra and the spectrum at specific frequencies for discrete spectra (line spectra) (Bendat and Piersol, 1986) and refers to the squared amplitude of the Fourier transform of a quantity at first order in the acoustic field variables (pressure, particle velocity) as a function of frequency. The spectrum, as opposed to the spectral density, is the appropriate frequency domain description for signals composed of discrete frequency components (e.g., periodic signals such as those composed of a set of tonals). In that case, the spectrum levels are independent of the FFT length as long as the length is sufficient to resolve all contributing components (and the signal’s time series does not change in character with change in the Fourier transform length). In contrast, the spectrum level of continuous spectra varies with varying FFT length since the amount of signal energy contained in each frequency bin changes with the binwidth and so actually represents a band spectral level. In calculating the spectrum from the Fourier transform, the phase is discarded so that a time series cannot be reconstructed from its spectrum. The pressure spectrum often is called the
power spectrum, but it is not a measure of acoustic power (nor of electrical power if the original time series is a voltage signal). The term power spectrum in almost all cases is a misnomer and should be avoided unless true power in the physics sense is being considered. The units of the spectrum are the square of the units of the time series; the pressure spectrum has units of pressure squared. In underwater acoustics the squared pressure is referenced to 1 µPa2 so that its spectrum in decibel units is dB re 1 µPa2. As determined by the definition of the decibel and the properties of the logarithm, the decibel units of the pressure spectrum are equivalent to dB re 1 µPa. Similarly, the acoustic particle velocity amplitude spectrum has decibel units of dB re 1 (m/s)2, equivalent to dB re 1 m/s.
The spectrum and spectral density of quantities at second order in the acoustic field variables, such as energy density, acoustic intensity, and acoustic power, are defined in terms of the spectra and spectral densities of the acoustic quantities at first order. For example, the potential energy density spectrum is equal to the pressure spectrum normalized by twice the adiabatic incompressibility, the kinetic energy density spectrum equals half the fluid ambient density times the particle velocity amplitude spectrum, and the acoustic intensity spectrum equals the cross-spectrum between the pressure and particle velocity (D’Spain et al., 1991). The acoustic power spectrum is the acoustic intensity spectrum integrated over a specified surface area.
ultrasonic—having a frequency above the human ear’s audibility limit of about 20,000 Hz used of waves and vibrations.
Temporal Character of Man-made Sounds
In Chapter 2, man-made sources were categorized according to the activity involved in creating the sound, for example, seismic surveying, shipping, sonar use. A second way of organizing the noise created by these sources is according to their frequency content, as is done in the introduction to Chapter 2. The following table presents a third way of grouping man-made sounds based on their temporal character. The table also contains a listing of common metrics for each of the four categories, followed by comments on some of them. Note that some metrics are not appropriate for certain classes of signals, as discussed below.
TABLE E-1 Man-made Sounds Grouped by Temporal Character
|
Temporal Character |
Some Common Metrics |
Examples of Man-made Sources |
|
Transient1 |
Time domain time series 0-pk amplitude2 pk-pk amplitude2 rise time total duration3 mean squared amplitude4 RMS amplitude4 squared amplitude summed over total duration5 |
explosions sonic booms1 |
|
|
Frequency Domain spectral density or spectrum |
|
|
Continuous in time, Periodic6 |
Frequency Domain frequencies of tonals spectral levels of tonals spectrum7 Time Domain maximum 0-pk amplitude maximum pk-pk amplitude mean squared amplitude rms amplitude |
discrete tone sonars (commonly used in research) ships: propeller cavitation tonals prop-driven aircraft blade tip tonals machinery and pumps: engine rotation tonals |
|
Periodic transient |
Time Domain duty cycle period all those under Transient |
sonars (commercial, military, research) seismic air-guns and arrays pile driving pingers and AHDs |
|
|
Frequency Domain repetition rate spectral density or spectrum of each transient |
|
|
Continuous in time, Aperiodic |
Time Domain mean squared amplitude rms amplitude 0-pk amplitude pk-pk amplitude |
broadband ship cavitation dredging icebreaking |
|
|
Frequency Domain spectral density7 |
|
|
1Transient can signify transient in time (of short duration) or transient in space (passing through a certain region in a short period of time), or both. For example, a moving source like a surface ship or a supersonic aircraft radiates sound continuously in time but creates transient-in-time signals recorded by a fixed receiver. Therefore, it is important to specify whether transient applies to the source characteristics or to the received field. 2The zero-to-peak and peak-to-peak amplitudes are illustrated for an air-gun array signal in the upper panel of Figure 2-4. 3The total time duration of a signal emitted by a source usually can be defined unambiguously. However, when it pertains to a received signal, the total duration can depend on the level of ocean noise with respect to the received signal level (“signal-to-noise ratio”) since noise can cover up the lower-level parts of the signal. In addition, propagation through the ocean can cause a change in the signal duration since the speed at which sound energy travels (“group velocity”) can be a function of frequency, a phenomenon called “dispersion.” Therefore, it is important to indicate clearly whether the signal duration is the duration emitted by the source or that measured at the receiver. This same point applies to all the other metrics in the table (see the discussion on source level versus received level in the Glossary). 4The time interval for the calculation of mean squared amplitude (the average of the squared amplitudes over a specified time interval) and root mean squared (RMS) amplitude (the square root of the mean squared amplitude) for a transient signal must be clearly specified in order for the quantity to be properly interpreted. 5Squared pressure integrated over the total signal duration is not equal to energy, as often stated. This issue is discussed in the “Physics of Sound” section. Rather, a more appropriate term might be “unweighted sound exposure.” According to ANSI (1994), the term sound exposure is the “time integral of squared instantaneous frequency-weighted sound pressure over a stated time interval or event.” The A-frequency weighting appropriate for human hearing sensitivity usually is used. However, no frequency weighing equivalent to unity weighting across the whole frequency band needs to be applied. Alternatively, a species-specific metric could be defined using a frequency weighting based on an audiogram (such as those plotted in Figure 1-1). 6When the term continuous is used, a clear distinction must be made between continuous in time and continuous in frequency. A continuous-in-time, periodic signal has a discrete spectrum, whereas a signal with a continuous-in-frequency spectrum can be either continuous-in-time and aperiodic or a transient-in-time domain. 7Spectrum and spectral density are defined in the “Spectral Analysis and the Frequency Domain” section of the Glossary. Note that a spectral density is not appropriate for sounds composed of a discrete set of tones (line spectra), since the spectral density level of a tone depends upon the FFT length. Conversely, the spectrum level of signals whose frequency content varies continuously with frequency (“continuous spectra”) also varies with FFT length, since the FFT length determines the bandwidth over which the signal energy is integrated (see the “Spectral Analysis and the Frequency Domain” section of the Glossary). In these cases, the FFT bandwidth must be reported since these levels actually are “band,” where the band is the FFT binwidth. |
A Few Specific Sources of Noise
Cavitation—the tearing apart of a fluid when the negative pressure (dilatation) becomes sufficiently large. This process causes the formation of bubbles and the radiation of sound (Urick, 1975). Cavitation imposes an upper limit to the maximum acoustic power output of a sonar system. For example, at 3 kHz at shallow depths, Urick indicates that the cavitation threshold is slightly more than 1 atm = 1.013 bar = 1.013 × 1011 µPa = 220 dB re 1 µPa. Some cavitation can be tolerated so that the maximum levels can be a factor of 2 to 3 greater than the threshold, suggesting a maximum level of slightly more than 230 dB re 1 µPa. One reason for constructing arrays of sources is to create higher equivalent source levels along the array main beam in the far field than could be achieved by a compact source because of the limitations imposed by cavitation.
Microseisms—naturally occurring noise created by the nonlinear interaction of oppositely propagating ocean surface waves. Oppositely propagating waves give rise to a standing wave pattern that radiates sound with twice the frequency of that of the interacting surface waves. Microseisms are the dominant natural noise source in the space- and time-averaged ocean noise spectra below 5-10 Hz. Seismologists created the term microseisms because they also are the dominant source of noise in high-quality, on-land seismometer measurements; however, their source mechanism is unrelated to seismic processes in the solid earth. The Wenz curves (Plate 1) list “Seismic Background” above “Surface Waves—Second-Order Pressure Effects,” but it is now known that the latter are the dominant source of prevailing ocean noise. Earthquakes and other tectonic processes contribute only intermittently.
Sonic Boom—a wave that is generated continuously by an object traveling faster than the speed of sound in the atmosphere. A sonic boom starts as a nonlinear shock wave with discontinuous jumps in pressure and fluid density. Because of dissipation and absorption, it eventually evolves into a linear acoustic wave at some distance from the source region. Its temporal character depends on the shape and size of the supersonic object, its speed, and its trajectory. The leading wavefront of a sonic boom is much like the bow wave of a surface ship, which is being “towed” along by the moving object. The sonic boom is a transient with respect to a receiver not traveling with the same velocity as the supersonic object creating the boom.
Thermal Noise—the pressure fluctuations associated with the thermal agitation of the ocean medium itself. It is what is left over when all other noise sources are removed and so provides the lowest bound for noise levels in the ocean. Thermal noise dictates the shape and level of ambient noise spectra above 50-100 kHz (depending on sea state; see Plate 1).
















