Appendix C
Supportive Breeding, Effective Population Size, and Inbreeding
Release of hatchery fish is practiced extensively in fisheries management either to protect weak populations from extinction or to sustain sport or commercial fisheries. To avoid the risk of compromising the genetic integrity of the recipient population, the fish released are frequently produced through captive breeding of a part of the wild population. A fraction of the wild fish are brought into captivity for reproduction, and their offspring are released into the natural habitat where they mix with wild individuals. This breeding practice, referred to as supportive breeding (Ryman and Laikre 1991), is intended to increase the census population size without introducing exogenous genes into the managed population.
Supportive breeding may increase the total population size through a higher reproductive output from the captive breeders than from those reproducing in the wild. In many situations, however, there is a trade-off between this demographic gain and the genetic “health” of the population, because the procedure of supportive breeding may be coupled with a reduction of the genetically effective population size (Ne), resulting in excessive inbreeding and loss of genetic variation. The basic reason for this reduction of Ne is that supportive breeding implies manipulating the reproductive rate of the captive (hatchery) segment of the population that results in a change of the variance of family size in the population as a whole (wild + captive), and this parameter is of critical importance to the effective size of the population (Ryman 1994, Ryman and Laikre 1991, Ryman et al. 1995b; Wang and Ryman 2001).
Rather complex theoretical considerations are sometimes required to predict the genetic dynamics of a population under supportive breeding, and for the purpose of this presentation, we confine the discussion to illustrating the basic problems by means of some worked examples. We focus on inbreeding (F) and on the corresponding parameter inbreeding effective size that is related to the rate of inbreeding per generation (ΔF) through ΔF = 1/(2Ne) (see Ryman et al. [1995b] or Wang and Ryman [2001 for details). The results presented below have been generated using the equations for inbreeding effective size of Wang and Ryman (2001).
Model: We consider a wild population with an even sex ratio that in a particular generation (t) consists of N individuals. Before mating, these N individuals (breeders) are distributed at random into a captive (c) and a wild (w) group of size Nc and Nw, which reproduce in captivity and in the wild, respectively (Nc + Nw = N; “enumeration” takes place at sexual maturity, and the unit of measurement refers to adults that are potential breeders). The mean and variance of the number of (adult) progeny per wild individual is μw and σ2w, respectively, and the corresponding quantities for the captive segment are μc and σ2c. The captive offspring are released into the natural habitat where they mix and breed with wild individuals. Mating is random within each of the wild and captive groups, and the entire process of selecting breeders for captive propagation and releasing their progeny may be repeated in generation t + 1 and subsequent generations. The wild population is of constant size when μw = 2, it grows when μw > 2, and it is declining if μw < 2. When considering the effect of supportive breeding on the total population size (N), the operation is successful when μc > μw, it has no effect when μc = μw, and it is unfavorable when μc < μw.
Binomial distribution of family size: As an example, we consider a natural population of N = 50 individuals that is constant in size (μw = 2). The organism can be bred in captivity, and under captive conditions, the average number of progeny is typically around 10 (μc = 10). Ecological studies indicate that the present population size is far below carrying capacity, and the manager wants to raise the number through captive propagation of some of the individuals. It is assumed that the removal of some individuals will not affect the reproductive rate of those that are left to reproduce in the wild. A supportive breeding program is initiated, and during each of 10 generations, five randomly selected breeders are caught in the wild and brought into captivity for reproduction and subsequent release of all their offspring (initial N = 50, Nc = 5, and Nw = N – 5 = 45).
The number of progeny per individual (family size) follows a binomial distribution within each of the wild and captive groups. Under such
conditions, the mean and variance of family size are approximately the same (σ2c ≈ μc σ2w ≈ μw), and the census and effective population sizes are identical (which follows from the definition of effective size).
Without interference, the effective size of the wild population would remain constant at Ne = N = 50 for each generation, because family size is binomially distributed. Under supportive breeding, the total size (N) of the population (wild + captive) grows linearly over time, but effective size behaves quite differently (Figure C-1a). Although the total population size (N) grows quickly, there is a sudden reduction of Ne in generation 2 below what it would have been without supportive breeding (Ne,2 ≈ 29). Further, although Ne grows larger after generation 2, the rate of increase is slower than that of the census size (N). The reason for this behavior of Ne is that the captive breeding program results in a change of demographic parameters that affect Ne. On one hand, the growing N tends to increase Ne. On the other, the differential contribution from wild and captive breeders (μw vs. μc) results in a variance for the population as a whole (σ2) that is larger than that without supportive breeding (σ2 = σ2w ≈ 2), which tends to reduce effective size. As N grows, σ2 declines asymptotically to σ2 ≈ 2, but in the first few generations, the increase of σ2 outweighs that of N, and effective size is reduced (Wang and Ryman 2001).
The reduction of Ne during the early stage of supportive breeding creates a “genetic bottleneck” that results in accumulation of inbreeding at a rate higher than that of a population left on its own. Thus, the boost of census size is obtained at the cost of increased inbreeding, and the effect of this increase may persist for many subsequent generations. The reason for this extended effect is that the overall genetic success of a supportive breeding operation cannot be judged exclusively from the number of generations required for Ne to exceed the value it had before the program was launched. Rather, evaluation of the total genetic impact of a breeding program must be based on the amount of inbreeding that has accumulated during the program as a whole.
The cumulative effects of supportive breeding on inbreeding can be assessed from the harmonic mean of Ne as indicated in Figure C-1a. As noted above, the effective number would stay constant at Ne = 50 in the absence of supportive breeding. As an effect of the breeding program, however, Ne first drops to a minimum in generation 2 and then starts to increase as the total population grows, and Ne exceeds 50 already in generation 4 when Ne,4 ≈ 58 (Figure C-1a). It is important to note, however, that this by no means implies that the population has now “recovered” from the excessive rate of inbreeding caused by the reduced effective size during the initial phase of the program. The reason is that the amount of inbreeding accumulating over multiple generations of variable Ne is de-
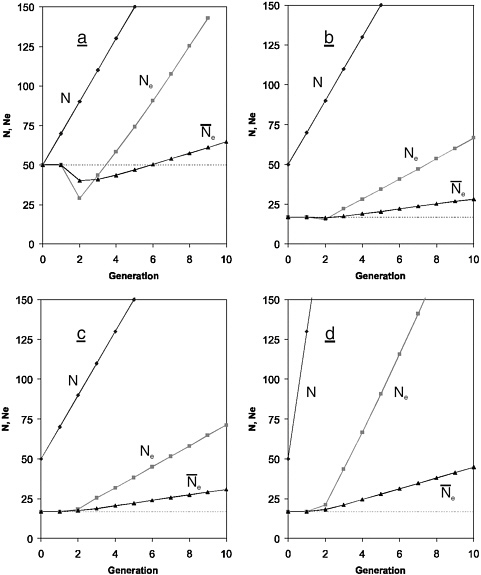
FIGURE C-1 Census size (N), effective size (Ne), and cumulative harmonic mean of effective size (![]() ) during 10 generations of supportive breeding in a population of 50 individuals that would be of constant size if left on its own (initial N = 50). In each generation a fixed number of Nc individuals are caught at random and brought into captivity for reproduction. The mean number of progeny per individual is μc = 10 in captivity and µw = 2 in the wild. Dashed lines indicate the effective size in the absence of supportive breeding. a, Nc = 5; the variance (σ2) of the number of the progeny per individual in the wild and in captivity are approximately equal to their respective means, i.e., σ2w ≈ µw = 2, and σ2c ≈ µc = 10. b, Nc = 5, σ2w = 10, and σ2c = 50. c, Nc = 5, σ2w = 10 and σ2c = 10. d, Nc = 20, σ2w = 10, and σ2c = 50.
) during 10 generations of supportive breeding in a population of 50 individuals that would be of constant size if left on its own (initial N = 50). In each generation a fixed number of Nc individuals are caught at random and brought into captivity for reproduction. The mean number of progeny per individual is μc = 10 in captivity and µw = 2 in the wild. Dashed lines indicate the effective size in the absence of supportive breeding. a, Nc = 5; the variance (σ2) of the number of the progeny per individual in the wild and in captivity are approximately equal to their respective means, i.e., σ2w ≈ µw = 2, and σ2c ≈ µc = 10. b, Nc = 5, σ2w = 10, and σ2c = 50. c, Nc = 5, σ2w = 10 and σ2c = 10. d, Nc = 20, σ2w = 10, and σ2c = 50.
termined by the harmonic mean of Ne over generations, and the harmonic mean is most heavily affected by the smaller of the values being averaged. In generation 4, this average is only about 43, implying that the population has accumulated more inbreeding during the first four generations than it would in the absence of supportive breeding, i.e., if the effective number had stayed constant at Ne = 50. It is not until generation 7 (at N7 = 190 and Ne,7 ≈ 108) that the harmonic mean of Ne exceeds 50, and the overall accumulation of inbreeding (total F) is less than it would have been had the population been left alone. Thus, although already the first six generations of this supportive breeding operation may be considered very successful in boosting both the census (N) and effective (Ne) numbers, the population still “suffers” from the genetic bottleneck that occurred during the first few generations of the program (Wang and Ryman 2001).
Under the present model the outcome of supportive breeding on Ne is qualitatively the same as that depicted in Figure C-1a in all situations where the number of progeny of wild and captive breeders is binomially distributed around their respective means of μw and µc (Ryman and Laikre 1991, Ryman et al. 1995b). The quantitative effects, however, i.e., the magnitude of the sudden drop in generation 2, the rate at which Ne increases in subsequent generations, and the time required for “recovery” depend on Nc, µw, µc, initial N, and the duration of the program. The severity of genetic bottleneck tends to be most pronounced when a small number of captive breeders are allowed to produce a large number of offspring over many generations. Expressed differently, the amount of “genetic damage” through accumulation of inbreeding is larger the more successful the support program is from a purely census perspective.
Nonbinomial distribution of family size: In natural populations of most organisms, including fishes, the variance of family size is frequently likely to be larger than binomial. The same is true for many captive populations unless active management measures are taken to reduce this variance. In such situations the effect of supportive breeding on Ne is more difficult to predict qualitatively, because the outcome now also depends on σ2w and σ2c, as exemplified in Figure C-1b. Here, the basic conditions are the same as in the previous example (Nc = 5; N = 50, and Nw = 45 at the start of the program; µw = 2 and µc = 10), except that the variances of family size are now five times larger than their binomial values with σ2w = 10 and σ2c = 50.
Under this latter scenario, the total (census) size of the population changes as in the previous example, as it should because Nc, µw, µc, and initial N are the same as before. The immediate reduction of Ne is quite small, however, and already in generation 3 the harmonic mean of Ne is larger (and the overall accumulation of inbreeding correspondingly smaller) than it would have been without supportive breeding. The rea-
son is that effective size is always smaller than census size in a population where the variance of family size exceeds its binomial value. Because of the larger than binomial variance in the present case, the wild population of 50 individuals (N = 50) only maintains an effective size of 17 (Ne ≈ 17) if left on its own, and the breeding program does not imply a change of the demographic parameters of the population as a whole (wild+captive) that brings Ne below its original value. Thus, for this particular population, the support program is successful both demographically and genetically, as it results in a rapid increase of both the census and the effective size.
The variance of family size can frequently be manipulated under captive conditions and efforts can be made to reduce this variance to increase the effective number of captive breeders (as is presently done in, for example, the Craig Brook hatchery). Reducing σ2c is expected to provide an increase of Ne in a population under supportive breeding, but the effect of such a reduction is minor in the present case. As indicated in Figure C-1c, bringing this variance down to σ2c = 10 (from its original value of σ2c = 50) only results in an increase of Ne from 15 to 18 in generation 2, and from 66 to 71 at the end of the program. For other combinations of wild and captive parameter values, the “genetic gain” of reducing σ2c may be substantial, however.
In contrast, for the combinations of mean and variances of family size in the present example (Figure C-1b) the breeding program could be made more successful by using more captive breeders, and Figure C-1d shows the result of increasing Nc from 5 to 20. Bringing a larger number of breeders into captivity not only boosts the census population more efficiently (as expected when µc > µw), but for the present parameters, it also results in a more rapid increase of the effective size and a correspondingly reduced accumulation of inbreeding (reflected in the larger harmonic mean Ne over the entire program).
Supportive breeding may drastically reduce the effective size of a population and thereby accelerate both the inbreeding and the loss of genetic diversity, also when the breeding program is successful in boosting the census population size. Predicting the genetic effects of a particular program may be quite complicated, however, requiring access to at least crude estimates of several parameters. The manager may have a quite good knowledge of the number of breeders brought into captivity and the mean and variance of the number of progeny they produce (Nc, μc, and σ2c), but the information on the corresponding quantities for the wild segment is frequently rather poor (but see Spidle et al (2003) for some recent estimates).
Clearly, the overall biological success of a supportive breeding program cannot be evaluated without assessing the impact on the effective size, and research efforts should be directed toward collection of data that
are necessary for realistic predictions of that impact. In this context, preliminary appraisals that are based on a range of seemingly realistic parameter values may be helpful in identifying critical information that may be missing.
The above examples are aimed at illustrating some of the basic genetic problems associated with supportive breeding, rather than providing an inventory of all the factors that should be considered when designing a breeding program. Situations not discussed include unsuccessful supportive breeding (i.e., μc < μw), declining wild populations (μw < 2), variable number of captive breeders, preferentially selecting individuals of wild or captive origin for captive breeding, overlapping generations, and populations that crash when the support program is terminated. Some of these aspects have been discussed in the literature, and in addition to the citations given above, interested parties should consult the papers by Duchesne and Bernatchez (2002), Hedrick et al. (2000), Lynch and O’Hely (2001), Waples and Do (1994), and references therein.







