Pore Pressure Induced by Fluid Injection
The dependence of the induced pore pressure on the operation parameters (injection rate, volume of fluid injected), on position and time, and on the hydraulic properties of the reservoir is illustrated in this appendix by considering the simple example of fluid injection in a disk-shaped reservoir. The analysis shows that different parameters control the pore pressure at the beginning of the injection operation and once enough fluid has been injected in the reservoir (see also Nicholson and Wesson, 1990).
The pore pressure induced by injection of fluid, Δρ, is to a good approximation governed by the diffusion equation
c∇2Δρ = ∂Δ/∂t + source
where c denotes the hydraulic diffusivity equal to c = k/μS. In the above, k is the intrinsic permeability of the rock (generally expressed in Darcy), μ is the fluid viscosity, and S is the storage coefficient, a function of the compressibility of both the fluid and the porous rock. The diffusion equation imposes a certain structure on the link between the magnitude of the induced pore pressure Δρ, the injected fluid volume V, and the rate of injection Qo.
As an example, we consider the injection of fluid at a constant volumetric rate Qo, at the center of a disk-shaped reservoir of thickness H and radius R. It is assumed that the reservoir is thin (i.e., H/R«1), and also that the pore pressure is uniform over the thickness of the layer, which implies, depending on the manner the fluid is injected, that some time has elapsed since the beginning of the operation.
At early time (to be defined more precisely later), the pore pressure perturbation induced by injection of fluid has not reached the boundary of the reservoir. The induced pore pressure field is then given by the source solution for an infinite domain, a solution of the form (Wang, 2000)
where r is the radial distance from the injection well, t is time, and F is a known function. The quantity where ρ* is a characteristic pressure (i.e., a yardstick for measuring the induced pressure) given by
Once the time elapsed since injection started becomes larger than a fraction, say 0.1, of the characteristic time t*=R2/c, then the evolution of the induced pore pressure becomes influenced by the finiteness of the reservoir. Formally, the pore pressure solution can then be expressed as
The function P(ρ,t) can be determined semianalytically. If the elapsed time t is expressed as the ratio of the injected volume V to the rate of injection Qo (i.e., t=V/Qo), then solution (2) can be written as
where 
is a characteristic fluid volume. The above expression suggests that the relationship between the induced pore pressure Δρ, the injected volume V, and the injection rate 
is not straightforward. However, Equation (3) shows important trends; for example, a decrease of the permeability causes an increase of the characteristic pressure, or an increase of the storage coefficient causes a decrease of the pore pressure, all other parameters kept constant.
At small time t«t*, the dimensionless pressure P = Δρ/ρ* reduces to the unbounded domain solution F, while at large time t»t*, the pressure tends to become uniform and the pore pressure is simply given by
as the function P(ρ,t) behaves for large t as P ≅ t/π. Thus, at large time, the pore pressure is simply proportional to the volume of injected fluid (Figure H.1). Equation (4) actually indicates that the large-time pore pressure is simply the ratio of the injected volume over the reservoir volume, divided by the storage coefficient.
The previous material provides some information about the link between pore pressure, injected volume, and injected rate for the particular case of an injector centered in a disk-shaped reservoir. These ideas can be generalized to more realistic cases. For example, for an arbitrarily shaped reservoir with n wells, each injecting at a rate , the general expression for the induced pore pressure can be written as
Δρ(x,t) = ρ*ς{x/L, t/t*;n, (xi, i = 1, n), reservoir shape}
where the characteristic pressure and time are given by
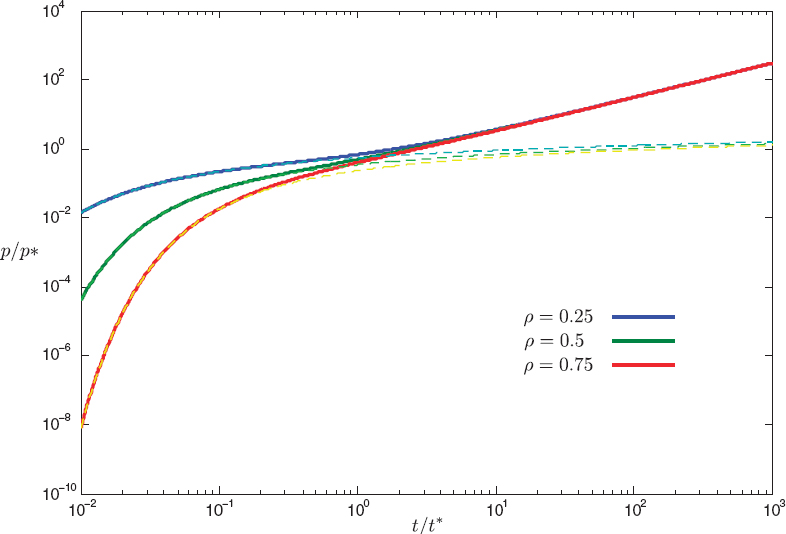
FIGURE H.1 Injection of fluid at a constant rate at the center of a disk-shaped reservoir. Plot of the dimensionless pore pressure Δρ/ρ* with respect to the dimensionless time t = t/t* (equal to V/V*) for three values of the dimensionless radius Q = r/R. This plot indicates that the pressure response is similar to the response of an unbounded reservoir as long as t ≤ 0.2 and that the pressure is approximately uniform and proportional to the volume of fluid injected when t ≥ 10. The dashed-line curves correspond to the solution F for an unbounded reservoir.
with L denoting a relevant length scale of the reservoir. Also x refers to the position of the field point, and xi to the position of the source i. At large time, the induced pore pressure is approximately given by
ρ ≅ V/(SVreservoir)
where V is the total volume of fluid injected 
and Vreservoir is the volume of the reservoir.
REFERENCES
Nicholson, C., and R.L. Wesson. 1990. Earthquake Hazard Associated with Deep Well Injection: A Report to the U.S. Environmental Protection Agency. U.S. Geological Survey Bulletin 1951, 74 pp.
Wang, H.F. 2000. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Princeton, NJ: Princeton University Press.
