A
Computational Modeling for SMART Vaccines
Scott Levin, Ph.D.
Johns Hopkins University
Estimates for the health and economic measures used to prioritize vaccine candidates in SMART Vaccines 1.0 are produced by a collection of formulas referred to as the computational submodel (see Figure 2-1). The submodel uses as its input data from the following parameters: demographic characteristics, disease burden, and vaccine characteristics (see Table 3-1). This section outlines the formulas and describes the multi-state population process model underlying these estimates. Health measures include premature deaths averted per year, incident cases prevented per year, quality-adjusted life years (QALYs) gained per year, and disability-adjusted life years (DALYs) averted per year. Economic measures include net direct costs (savings) of vaccine use per year, workforce productivity gained per year, one-time costs, and cost-effectiveness in cost per QALY or cost per DALY (see Table S-1).
Central to interpreting each health and economic measure is an understanding of the populations being compared, the time-scale applied, and the estimate formulation. The underlying population process model is described below, followed by a detailed account of the estimation procedures.
The Population Process Model
The mathematical framework underlying SMART Vaccines was developed in Phase I and has been enhanced to result in the present software, a comprehensive explanation about the model is provided in the second and third chapters of the Phase I report, Ranking Vaccines: A Prioritization Framework (IOM, 2012). The SMART Vaccine 1.0 population process model uses a cohort component method to project populations forward at yearly intervals (Preston et al., 2001) The yearly aging process is simulated for both a baseline population with no vaccine (i.e., the control) and a test population with either (1) the vaccine in approximated steady state delivery or (2) the vaccine having been newly introduced, and the two populations are compared. Table A-1, provides a comprehensive description of these three population vaccine conditions. It is through comparing a vaccinated population to the baseline that the various health and economic measures are estimated over the appropriate time-scale.
The model assumes a constant number of infants entering the population each year, with the number being given by the number of infants (i.e.,
TABLE A-1
Population Comparison in the SMART Vaccines Process Model
| Population | Description |
| Baseline | The baseline population is the reference for comparison. Vaccines not yet developed and those used in SMART Vaccines 1.0 have a baseline population in which no vaccine has been used. However, in cases where a vaccine does exist, the baseline population may reflect the current vaccination state as reference against which to compare hypothetical newly developed vaccines for the same disease that have different (i.e., more desirable) characteristics. |
| Vaccine in approximated steady state delivery | In a population in which the vaccine is being administered under the steady state approximation it is assumed that individuals of all ages have had the opportunity (i.e., accounting for coverage) to receive the vaccine. For example, in the case of a vaccine that solely targets infants, individuals of all ages are assumed to have had the opportunity for vaccination. Achieving steady state for an infant vaccination would require many years, unlike the case with a vaccine designed for delivery to all ages. |
| Vaccine first being introduced | In the case of a vaccine first being introduced into a population it is assumed that the vaccine was delivered solely to the target population (i.e., accounting for coverage) at model initialization. No other members of the population will have had the opportunity to have received the vaccine. |
age less than 1) present in the World Health Organization (WHO) population life-table input (WHO, 2013). This is operationalized by assuming that the number of infants (i.e., children under age one) observed at baseline will remain constant in the future. This assumption eventually produces a stationary age distribution, but the total population size eventually reached will be somewhat different from that of a population immediately reaching replacement fertility (Preston et al., 2000). Information on population below age 1 is taken from WHO population life-table input. Individuals may exit the population by death caused by disease or by all other causes. The model does not account for migration of any sort. The committee chose to use this simplified version of the population process in light of the constraints present in the early development phase of SMART Vaccines 1.0. The model minimizes assumptions regarding population dynamics and, consequently, reduces the burden of data entry, making it easier to use. It is expected that this simplified version will serve as a foundation upon which more complex population processes may be constructed as SMART Vaccines advances.
The step-by-step computations of the population process model are as follows. The model is initialized at time zero t0, which corresponds to the year of the population data that are input into the model (e.g., 2009 for the vaccine candidates). At initialization, linear interpolation is used to produce a population age distribution in 1-year increments from the standard WHO life-table format, which is in 5-year increments. Age-specific probabilities of dying from all causes, nqx, are computed; the subscript x refers to the age at the beginning of the age interval, and the subscript n refers to the length of the interval. The probabilities for dying in a given 1-year time period, 1qx, are derived from the number of individuals alive at each age, lx, along with the probability of survival and the death rate between ages x and x+n, written as npx and nMx, respectively. The following equations are used to estimate yearly nq1 (Preston et al., 2001):
![]()
The process model directly computes age-specific population parameters, including population size N; population size disease-eligible NE (i.e., that part of the population that has not previously been permanently impaired by the disease); and the subset of the population targeted to receive vaccination, TI or TS, as seen in Table A-2: Population Parameters. At each yearly interval starting with t0 the population is composed of individuals in mutually exclusive vaccination states. These states are the
TABLE A-2
Population Process Model
| Population Parameters | Baseline0 | With Vaccine1 | Impact |
| Population size (N) | nNx0 = nNx-10 - nDAx-10 | nNx1 = nNx-11 - nDAx-11 | nNx1 - nNx0 |
| Population size disease eligible (NE) | nNEx0 = nNx-10 - nCPx-10 | nNEx1 = nNx-11 – nCPx-11 | nNEx1 - nNEx0 |
| Target population (TI) Vaccine in Steady State | nTSx0 = 0 | nTSx1 = nNEx x 1 | nTSx1 |
| Target population (TS) Vaccine Introduced | nTIx0 = 0 | nTIx1 = nNEx x nTARGx | nTIx1 |
| Vaccination States | Baseline0 | With Vaccine1 | Impact |
| Vaccinated immune (V) | nVx0 = 0 | nVx1 = nTx1 x nCOVx x nEFFx | nVx1 |
| Vaccinated susceptible (VS) | nVSx0 = 0 | nVSx1 = nTx1 x nCOVx x (1 - nEFFx) | nVSx1 |
| Unvaccinated immune (B) | nBx0 = 0 | If ∑ (nCOVx x nNx0) / ∑nNx0 > 80% nBx1 = (nNEx1 -nVx1 -nVSx1) x nEFFx Else nBx1 = 0 | nBx1 |
| Unvaccinated susceptible (BS) | nBSx0 = nNx0 | nBSx1 = nNEx1 - (nVx1 + nVSx1 + nBx1) | nBSx0 – nBSx1 |
| Health Events | Baseline0 | With Vaccine1 | Impact |
| Total cases (C) | nCx0 = nNEx0 x nINCx | nCx1 = (nVSx1 + nBSx1) x nINCx | nCx0 – nCx1 |
| Deaths by disease (D) | nDx0 = nCx0 x nCFRx | nDx1 = nCx1 x nCFRx | nDx0 – nDx1 |
| Cases: Impairment (CP) | nCPx0 = (nCx0 -nDx0) x nIPx | nCPx1 = (nCx1 - nDx1) x nIPx | nCPx0 – nCPx1 |
| Cases: Morbidity (CM) | nCMx0 = nCx0 - nDx0 - nCPx0 | nCMx1 = nCx1 - nDx1 - nCPx1 | nCMx0 – nCMx1 |
| All-cause deaths (including deaths caused by disease) (DA) | nDAx0 = nNEx0 x nqx0 | nDAx1 = nNEx1 x nqx0 - (nDx0 - nDx1) | nDAx0 – nDAx1 |
NOTE: CFR = annual case fatality risk; COV = coverage; EFF = effectiveness; INC = annual incidence proportion; IP = annual case impairment risk; TARG = target proportion.
vaccinated immune, V; the vaccinated susceptible, VS; the unvaccinated immune, B (i.e., those who may have indirect protection through herd immunity); and the unvaccinated susceptible, BS (Table A-2: Vaccination States). No members of the population belong to the vaccinated immune, vaccinated susceptible, or unvaccinated immune states in a baseline population when a vaccine is not in existence. Various “health events” occur each year and are computed based on parameters set by user input (e.g., disease incidence, vaccination effectiveness, etc.). These events include the number of disease cases, C; deaths by the disease, D; diseases cases leading to permanent impairment, CP; disease cases leading to morbidity, CM (i.e., complete recovery by year end); and all-cause deaths, DA. The mathematical formulas for these measures are displayed in Table A-2. The superscript 0 refers to the simulated baseline population, as opposed to the simulated population with vaccine 1. Vaccinated populations may be either in the steady state delivery approximation or in the vaccine newly introduced state.
The model described in Table A-2 has several notable characteristics. First, the calculated value for the population size disease-eligible (NE) may vary from year to year. The difference from one year to the next is the number of people in the population who were permanently impaired in the intervening year. For example, if a member of the population contracts tuberculosis and, as a result, has permanent lung impairment, that person is not eligible to contract the same disease in subsequent years (i.e., not disease-eligible).
Next, the variable T that represents the target population is used to distinguish populations (see Table A-1). For example, no proportion of the baseline population receives the vaccine; therefore the corresponding target multiplier nTARGx equals zero for all ages. This serves as a proxy for scenarios in which the vaccine does not exist. By contrast, populations assumed to have reached steady state vaccine delivery have an target multiplier of one for all ages. This may be interpreted as an initialization state in which all members of the current population (i.e., all ages) have had the opportunity to receive the vaccination (i.e., coverage rates apply) at t0. Alternatively, in populations where the vaccine is newly introduced, delivery proceeds only for the age-specific target population specified at input nTARGx. For example, consider the influenza vaccine, for which there is no difference between steady state delivery and the introduction of a new vaccine. The two states are equivalent because the vaccine targets the entire population (i.e., all ages) each year. By contrast, a vaccine candidate for tuberculosis may be designed to target only infants, which will create a major difference between initialization states.
The effect of herd immunity is incorporated into the process model for contagious diseases with human-to-human transmission. In particular, the effect is represented by the presence of an unvaccinated immune population B that may receive the benefits of indirect protection (see Table A-2). If the user chooses to apply herd immunity, the overall coverage within the population is calculated. If this coverage is greater than or equal to 80 percent, the entire unvaccinated susceptible population BS receives indirect protection. Receiving disease immunity through indirect protection is treated identically to receiving the vaccine and is conferred in accordance with the vaccine’s effectiveness. If overall coverage is less than 80 percent, no indirect protection is assumed.
Finally, a connection exists between the baseline and the vaccine comparison process models. The number of all-cause deaths with disease, DA, for a vaccinated population is equal to tbe number of all-cause deaths in the baseline population minus the number of deaths prevented by the vaccine in that year. The same age-specific all-cause mortality rates are applied to both populations (i.e., the baseline and the vaccinated), and the prevented deaths, nDx0 – nDx1, are subtracted out for the case of the vaccinated population, as can be seen in Table A-2. Thus, the resultant deaths DA diverge, and the difference is projected forward each year of the simulation.
Health and Economic Measures
Health and economic estimates are computed using the population process model comparisons as their basis (Table A-2: Impact). However, understanding the populations in comparison and the time scale applied is fundamental to interpreting the meaning of each individual measure. Table A-3 displays this context for each of the nine health and economic measures.
Measures that apply to the steady-state delivery approximation are calculated for the 1-year time period after initialization; each of these measures is distinguished by a “per year” phrasing (see Table A-3). Cost-effectiveness measures such as cost per QALY gained or cost per DALY averted are computed over a 100-year time horizon for those populations first being introduced to the vaccine (see Table A-3). If desired, the user can choose to apply a lesser time horizon through the SMART Vaccines 1.0 interface. The one-time costs measure is designed to capture the estimated total costs for research, development, and licensure of the new vaccine. This is input directly as more than $1 billion, $500 million to $1 billion, $100 million to $500 million, or less than $100 million. One-time costs are interpreted as taking place over the period of time until vaccine adoption, which is provided by user input.
TABLE A-3
Comparator Populations and Time Scale
|
Vaccine in Steady State Approximation Time Scale: 1-year horizon |
Vaccine First Introduced Time Scale: 100 years, or a user-defined horizon less than 100 years |
| Premature deaths averted per year | Cost-effectiveness in cost per QALY gained |
| Incident cases prevented per year | Cost-effectiveness in cost per DALY averted |
| QALYs gained per year | |
| DALYs averted per year | |
| Net direct costs of vaccine use per year | |
| Workforce productivity gained per year | |
| One-time costs Time scale: Applied over time to adoption (user defined) |
NOTE: DALYs = disability-adjusted life years; QALYs = quality-adjusted life years.
The formulas for each health and economic estimate are shown in Table A-4. The notations correspond to the definitions presented in Table A-2.
Discounting is applied to both the health and the economic measures, with a default annual rate of 3 percent, and the user can modify the annual rate or eliminate the discounting altogether by setting the annual rate to zero. Further aggregate discounting is applied to the cost-effectiveness measures only in order to account for time to adoption (see Table A-3). The duration (nDurationx) used to produce the health and economic estimates (see Table A-4) varies by measure. The durations for QALYs and DALYs due to morbidity are input by the user and can be no longer than one year. Individuals with a disease that causes morbidity are assumed to completely recover by year’s end. The durations used for QALYs due to death or permanent impairment are given by the age-specific future life expectancy, adjusted and discounted by the health utilities index (HUI2). The durations used for DALYs due to death or permanent impairment similarly use discounted life expectancy but are based on the standard life expectancy and remain unadjusted for HUI2. The durations due to morbidity used for workforce productivity calculations are input by the user and are identical to the time-periods used for QALYs and DALYs. However, workforce productivity loss due to death or permanent impairment is assumed to be six months. This is the average duration over the 1-year projection inter-
TABLE A-4
Health and Economic Formulas
| Measure | Formula |
| Premature deaths averted | ∑nDx0 – nDx1 |
| Incident cases averted | ∑ nCx0 – nCx1 |
| Quality-adjusted life years (QALYs) gained | ∑nQALYx0(Death + Impairment + Morbidity) – ∑nQALYx1(Death + Impairment + Morbidity) nQALYx(Death) = (nQALYx0D - nQALYx1D) x nDurationx nQALYx(Impairment) = (nQALYx 0CP - nQALYx1CP) x nTollx x nDurationx nQALYx(Morbidity) = (nQALYx0CM - nQALYx1CM) x nTollx x nDurationx |
| Disability-adjusted life years (DALYs) averted (Rushby and Hanson, 2001) | ∑nDALYx0(Death + Impairment + Morbidity) – ∑nDALYx1(Death + Impairment + Morbidity) DALYs = years of life lost (YLL) + years of life lived with disability (YLD) YLD or YLL (W=1) = W 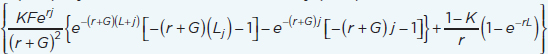 nDALYx(Death) = (nDALYx0D – nDALYx1D) x nYLLx nDALYx(Impairment) = (nDALYx0CP – nDALYx1CP) x nYLDx nDALYx(Morbidity) = (nDALYx0CM – nDALYx1CM) x nYLDx K = age weight modulation factor (0 = off, 1 = on); F = constant (0.1658); r = discount rate; j = age of death (YLL) or age of onset of disability (YLD); G = parameter form the age weighting function (0.04); L = standard expectation of life at age a (YLL) or duration of disability (YLD); W = disability weight (YLD) |
| Net direct costs (savings) of vaccine use | ∑nDeliveryCostsx – ∑nHealthcareCostsx nDeliveryCostsx= [(nVx1 +nVSx1) x doses x (dose cost x cost to administer)]/length of immunity nHealthcareCostsx = nHealthCarex0(Death + Impairment + Morbidity) – nHealthCarex1(Death + Impairment + Morbidity) nHealthcareCostsx(Death) = (nDx0D – nDx1D) x ∑nCostOfServicesx nHealthcareCostsx(Impairment) = (nCPx0D – nCPx1D) x ∑nCostOfServicesx x nDurationx nHealthcareCostsx(Morbidity) = (nCMx0D – nCMx1D) x ∑nCostOfServicesx x nDurationx |
| Workforce productivity (WP) gained | ∑nWPx0(Death + Impairment + Morbidity) – nWPx1(Death + Impairment + Morbidity) nWPx(Death) = (nDx0D – nDx1D) x nHourlyWagex x 2000 hours x nDurationx nWPx(Impairment) = (nCPx0D – nCPx1D) x nHourlyWagex x 2000 hours x nDurationx nWPx(Morbidity) = (nCMx0D – nCMx1D) x nHourlyWagex x 2000 hours x nDurationx |
| Cost-effectiveness | QALYs / Net Direct Costs (Savings) or DALYs / Net Direct Costs (Savings) |
vals. In short, workforce loss calculations are limited to one year and do not account for future years lost for those who experience death or permanent impairment.
Model Limitations and Further Work
The computational model that underpins SMART Vaccines has a few limitations that would benefit from improvements in subsequent versions. First, closing the population process to migration does not allow the model to account for population dynamics that may influence health and economic measures, especially for cost-effectiveness modeled over a 100-year time horizon. However, this basic design does reduce user assumptions and the practical burden of data entry, and it leads to results that can be interpreted as vaccine impacts exclusive to the current population, with minimal confounders.
Second, the steady-state approximation does not account for changes in the population that may occur by the time steady-state vaccine delivery is reached. As the time to steady state increases (e.g., it is longer for tuberculosis than for influenza), so does the potential for inaccurate estimation. Given this limitation, we chose to model an immediate steady-state proxy because the purpose of vaccine intervention is to swiftly achieve steady state and to maximize health benefits. This ultimate purpose was deemed most significant to the prioritization exercise, so we chose to keep this exercise free from the complications that may be inevitable during vaccine ramp-up periods.
Finally, a limitation exists in the level of detail required for the disease and the vaccine characteristics specified as input. Under some circumstances, the input required may appear coarse in order to capture specific details of a disease. In these cases data input may be altered to produce a desired average effect, or the use of pre-defined special populations may be used.
A good understanding of the modeling concepts within SMART Vaccines 1.0 will allow adept users to treat input data appropriately and to capture the complexities of different diseases and vaccines that are not apparent through data input interfaces. Overall, the committee wished to balance the complexity of the modeling and data requirements against the model’s capabilities in order to accurately characterize a broad range of diseases and vaccines and software usability. In short, SMART Vaccines 1.0 is designed to serve as a foundation for further work in this area.
References
IOM (Institute of Medicine). 2012. Ranking Vaccines: A prioritization framework: Phase I: Demonstration of concept and a software blueprint. Washington, DC: The National Academies Press.
Preston, H., P. Heuveline, and M. Guillot. 2001. Demography: Measuring and modeling population processes. Malde, MA: Blackwell.
Rushby, J. A., and K. Hanson. 2001. Calculating and presenting disability adjusted life years (DALYs) in cost-effectiveness analysis. Health Policy and Planning 16(3):326–331.
WHO (World Health Organization). 2013. Life tables. http://tinyurl.com/cd2lpou (accessed May 11, 2013).












