Connections Between the Mathematical Sciences and Other Fields
In addition to ascertaining that the internal vitality of the mathematical sciences is excellent, as illustrated in Chapter 2, the current study found a striking expansion in the impact of the mathematical sciences on other fields, as well as an expansion in the number of mathematical sciences subfields that are being applied to challenges outside of the discipline. This expansion has been ongoing for decades, but it has accelerated greatly over the past 10-20 years. Some of these links develop naturally, because so much of science and engineering now builds on computation and simulation for which the mathematical sciences are the natural language. In addition, data-collection capabilities have expanded enormously and continue to do so, and the mathematical sciences are innately involved in distilling knowledge from all those data. However, mechanisms to facilitate linkages between mathematical scientists and researchers in other disciplines must be improved.
The impacts of mathematical science research can spread very in some cases, because a new insight can quickly be embodied in software without the extensive translation steps that exist between, say, basic research in chemistry and the use of an approved pharmaceutical. When mathematical sciences research produces a new way to compress or analyze data, value financial products, process a signal from a medical device or military system, or solve the equations behind an engineering simulation, the benefit can be realized quickly. For that reason, even government agencies or industrial sectors that seem disconnected from
the mathematical sciences have a vested interest in the maintance of a strong mathematical sciences enterprise for our nation. And because that enterprise must be healthy in order to contribute to the supply of well-trained individuals in science, technology, engineering, and mathematical (STEM) fields, it is clear that everyone should care about the vitality of the mathematical sciences.
This chapter discusses how increasing interaction with other fields has broadened the definition of the mathematical sciences. It then documents the importance of the mathematical sciences to a multiplicity of fields. In many cases, it is possible to illustrate this importance by looking at major studies by the disciplines themselves, which often list problems with a large mathematical sciences component as being among their highest priorities. Extensive examples of this are given in Appendix D.
BROADENING THE DEFINITION OF THE MATHEMATICAL SCIENCES
Over the past decade or more, there has been a rapid increase in the number of ways the mathematical sciences are used and the types of mathematical ideas being applied. Because many of these growth areas are fostered by the explosion in capabilities for simulation, computation, and data analysis (itself driven by orders-of-magnitude increases in data collection), the related research and its practitioners are often assumed to fall within the umbrella of computer science. But in fact people with varied backgrounds contribute to this work. The process of simulation-based science and engineering is inherently very mathematical, demanding advances in mathematical structures that enable modeling; in algorithm development; in fundamental questions of computing; and in model validation, uncertainty quantification, analysis, and optimization. Advances in these areas are essential as computational scientists and engineers tackle greater complexity and exploit advanced computing. These mathematical science aspects demand considerable intellectual depth and are inherently interesting for the mathematical sciences.
At present, much of the work in these growth areas—for example, bioinformatics, Web-based companies, financial engineering, data analytics, computational science, and engineering—is handled primarily by people who would not necessarily be labeled “mathematical scientists.” But the mathematical science content of such work, even if it is not research, is considerable, and therefore it is critical for the mathematical sciences community to play a role, through education, research, and collaboration. People with mathematical science backgrounds per se can bring different perspectives that complement those of computer scientists and others, and the combination of talents can be very powerful.
There is no precise definition of “the mathematical sciences.” The following definition was used in the 1990 report commonly known as the David II report after the authoring committee’s chair, Edward E. David:
The discipline known as the mathematical sciences encompasses core (or pure) and applied mathematics, plus statistics and operations research, and extends to highly mathematical areas of other fields such as theoretical computer science. The theoretical branches of many other fields—for instance, biology, ecology, engineering, economics—merge seamlessly with the mathematical sciences.1
The 1998 Odom report implicitly used a similar definition, as embodied in Figure 3-1, adapted from that report.
Figure 3-1 captures an important characteristic of the mathematical sciences—namely, that they overlap with many other disciplines of science, engineering, and medicine, and, increasingly, with areas of business such as finance and marketing. Where the small ellipses overlap with the main ellipse (representing the mathematical sciences), one should envision a mutual entwining and meshing, where fields overlap and where research and people might straddle two or more disciplines. Some people who are clearly affiliated with the mathematical sciences may have extensive interactions and deep familiarity with one or more of these overlapping disciplines. And some people in those other disciplines may be completely comfortable in mathematical or statistical settings, as will be discussed further. These interfaces are not clean lines but instead are regions where the disciplines blend. A large and growing fraction of modern science and engineering is “mathematical” to a significant degree, and any dividing line separating the more central and the interfacial realms of the mathematical sciences is sure to be arbitrary. It is easy to point to work in theoretical physics or theoretical computer science that is indistinguishable from research done by mathematicians, and similar overlap occurs with theoretical ecology, mathematical biology, bioinformatics, and an increasing number of fields. This is not a new phenomenon—for example, people with doctorates in mathematics, such as Herbert Hauptman, John Pople, John Nash, and Walter Gilbert, have won Nobel prizes in chemistry or economics—but it is becoming more widespread as more fields become amenable to mathematical representations. This explosion of opportunities means that much of twenty-first century research is going to be built on a mathematical science foundation, and that foundation must continue to evolve and expand.
______________________
1 NRC, 1990, Renewing U.S. Mathematics: A Plan for the 1990s. National Academy Press, Washington, D.C.
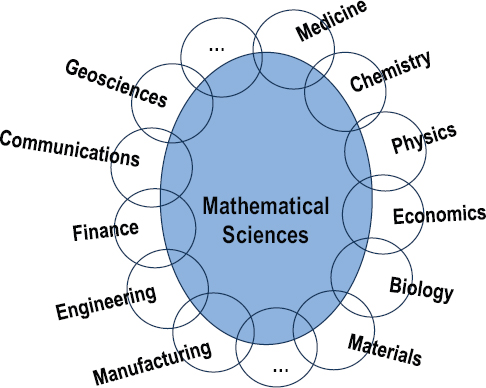
FIGURE 3-1 The mathematical sciences and their interfaces. SOURCE: Adapted from National Science Foundation, 1998, Report of the Senior Assessment Panel for the International Assessment of the U.S. Mathematical Sciences, NSF, Arlington, Va.
Note that the central ellipse in Figure 3-1 is not subdivided. The committee members—like many others who have examined the mathematical sciences—believe that it is important to consider the mathematical sciences as a unified whole. Distinctions between “core” and “applied” mathematics increasingly appear artificial; in particular, it is difficult today to find an area of mathematics that does not have relevance to applications. It is true that some mathematical scientists primarily prove theorems, while others primarily create and solve models, and professional reward systems need to take that into account. But any given individual might move between these modes of research, and many areas of specialization can and do include both kinds of work. Overall, the array of mathematical sciences share a commonality of experience and thought processes, and there is a long history of insights from one area becoming useful in another.
Thus, the committee concurs with the following statement made in the 2010 International Review of Mathematical Sciences (Section 3.1):
A long-standing practice has been to divide the mathematical sciences into categories that are, by implication, close to disjoint. Two of the most common distinctions are drawn between “pure” and “applied” mathematics, and between “mathematics” and “statistics.” These and other categories can be useful to convey real differences in style, culture and methodology, but in the Panel’s view, they have produced an increasingly negative effect when the mathematical sciences are considered in the overall context of science and engineering, by stressing divisions rather than unifying principles. Furthermore, such distinctions can create unnecessary barriers and tensions within the mathematical sciences community by absorbing energy that might be expended more productively. In fact, there are increasing overlaps and beneficial interactions between different areas of the mathematical sciences. . . . [T]he features that unite the mathematical sciences dominate those that divide them.2
What is this commonality of experience that is shared across the mathematical sciences? The mathematical sciences aim to understand the world by performing formal symbolic reasoning and computation on abstract structures. One aspect of the mathematical sciences involves unearthing and understanding deep relationships among these abstract structures. Another aspect involves capturing certain features of the world by abstract structures through the process of modeling, performing formal reasoning on these abstract structures or using them as a framework for computation, and then reconnecting back to make predictions about the world—often, this is an iterative process. A related aspect is to use abstract reasoning and structures to make inferences about the world from data. This is linked to the quest to find ways to turn empirical observations into a means to classify, order, and understand reality—the basic promise of science. Through the mathematical sciences, researchers can construct a body of knowledge whose interrelations are understood and where whatever understanding one needs can be found and used. The mathematical sciences also serve as a natural conduit through which concepts, tools, and best practices can migrate from field to field.
A further aspect of the mathematical sciences is to investigate how to make the process of reasoning and computation as efficient as possible and to also characterize their limits. It is crucial to understand that these different aspects of the mathematical sciences do not proceed in isolation from one another. On the contrary, each aspect of the effort enriches the others with new problems, new tools, new insights, and—ultimately—new paradigms.
Put this way, there is no obvious reason that this approach to knowledge should have allowed us to understand the physical world. Yet the entire
______________________
2 Engineering and Physical Sciences Research Council (EPSRC), 2010, International Review of Mathematical Science. EPSRC, Swindon, U.K., p. 10.
mathematical sciences enterprise has proven not only extraordinarily effective, but indeed essential for understanding our world. This conundrum is often referred to as “the unreasonable effectiveness of mathematics,” mentioned in Chapter 2.
In light of that “unreasonable effectiveness,” it is even more striking to see, in Figure 3-2, which is analogous to Figure 3-1, how far the mathematical sciences have spread since the Odom report was released in 1998.
Reflecting the reality that underlies Figure 3-2, this report takes a very inclusive definition of “the mathematical sciences.” The discipline encompasses the broad range of diverse activities related to the creation and analysis of mathematical and statistical representations of concepts, systems, and processes, whether or not the person carrying out the activity identifies as a
mathematical scientist. The traditional areas of the mathematical sciences are certainly included. But many other areas of science and engineering are deeply concerned with building and evaluating mathematical models, exploring them computationally, and analyzing enormous amounts of observed and computed data. These activities are all inherently mathematical in nature, and there is no clear line to separate research efforts into those that are part of the mathematical sciences and those that are part of computer science or the discipline for which the modeling and analysis are performed.3 The committee believes the health and vitality of the discipline are maximized if knowledge and people are able to flow easily throughout that large set of endeavors.
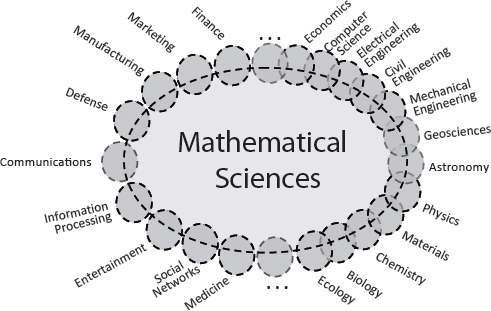
FIGURE 3-2 The mathematical sciences and their interfaces in 2013. The number of interfaces has increased since the time of Figure 3-1, and the mathematical sciences themselves have broadened in response. The academic science and engineering enterprise is suggested by the right half of the figure, while broader areas of human endeavor are indicated on the left. Within the academy, the mathematical sciences are playing a more integrative and foundational role, while within society more broadly their impacts affect all of us—although that is often unappreciated because it is behind the scenes. This schematic is notional, based on the committee’s varied and subjective experience rather than on specific data. It does not attempt to represent the many other linkages that exist between academic disciplines and between those disciplines and the broad endeavors on the left, only because the full interplay is too complex for a two-dimensional schematic.
So what is the “mathematical sciences community”? It is the collection of people who are advancing the mathematical sciences discipline. Some members of this community may be aligned professionally with two or more disciplines, one of which is the mathematical sciences. (This alignment is reflected, for example, in which conferences they attend, which journals they publish in, which academic degrees they hold, and which academic departments they belong to.) There is great value in the mathematical sciences welcoming these “dual citizens”; their involvement is good for the mathematical sciences, and it enriches the ways in which other fields can approach their work.
The collection of people in the areas of overlap is large. It includes statisticians who work in the geosciences, social sciences, bioinformatics, and other areas that, for historical reasons, became specialized offshoots of statistics. It includes some fraction of researchers in scientific computing and computational science and engineering. It includes number theorists who contribute to cryptography, and real analysts and statisticians who contribute to machine learning. It includes operations researchers, some computer scientists, and physicists, chemists, ecologists, biologists, and economists who rely on sophisticated mathematical science approaches. Some of the engineers who advance mathematical models and computational simulation are also included. It is clear that the mathematical sciences now extend far beyond the definitions implied by the institutions—academic departments, funding sources, professional societies, and principal journals—that support the heart of the field.
As just one illustration of the role that researchers in other fields play in the mathematical sciences, the committee examined public data4 on National Science Foundation (NSF) grants to get a sense of how much of the research supported by units other than the NSF Division of Mathematical
______________________
3 Most of the other disciplines shown in Figure 3-2 also have extensive interactions with other fields, but the full interconnectedness of these endeavors is omitted for clarity.
4 Available at http://www.nsf.gov/awardsearch/.
Sciences (DMS) has resulted in publications that appeared in journals readily recognized as mathematical science ones or that have a title strongly suggesting mathematical or statistical content. While this exercise was necessarily subjective and far from exhaustive, it gave an indication that NSF’s support for the mathematical sciences is de facto broader than what is supported by DMS. It also lent credence to the argument that the mathematical sciences research enterprise extends beyond the set of individuals who would traditionally be called mathematical scientists. This exercise revealed the following information:
• Grants awarded over the period 2008-2011 by NSF’s Division of Computing and Communication Foundations (part of the Directorate for Computer and Information Science and Engineering) led to 262 publications in the areas of graphs and, to a lesser extent, foundations of algorithms.
• Grants awarded over 2004-2011 by the Division of Physics led to 148 publications in the general area of theoretical physics.
• Grants awarded over 2007-2011 by the Division of Civil, Mechanical, and Manufacturing Innovation in NSF’s Engineering Directorate led to 107 publications in operations research.
This cursory examination also counted 15 mathematical science publications resulting from 2009-2010 grants from NSF’s Directorate for Biological Sciences. (These publication counts span different ranges of years because the number of publications with apparent mathematical sciences content varies over time, probably due to limited-duration funding initiatives.) For comparison, DMS grants that were active in 2010 led to 1,739 publications. Therefore, while DMS is clearly the dominant NSF supporter of mathematical science research, other divisions contribute in a nontrivial way.
Analogously, membership figures from the Society for Industrial and Applied Mathematics (SIAM) demonstrate that a large number of individuals who are affiliated with academic or industrial departments other than mathematics or statistics nevertheless associate themselves with this mathematical science professional society. Figure 3-3 shows the departmental affiliation of SIAM’s nonstudent members.
A recent analysis tried to quantify the size of this community on the interfaces of the mathematical sciences.5 It found that faculty members in 50 of the top U.S. mathematics departments—who would therefore be in the central disk in Figure 3-2—have published in aggregate some 64,000 research papers since 1971 that have been indexed by Zentralblatt MATH (and thus can be inferred to have mathematical content). Over the same period, some 75,000 research papers indexed by Zentralblatt MATH were published by faculty members in other departments of those same 50 universities. The implication is that a good deal of mathematical sciences research—as much as half of the enterprise—takes place outside departments of mathematics.6 This also suggests that the scope of most mathematics departments may not mirror the true breadth of the mathematical sciences.
______________________
5 Joseph Grcar, 2011, Mathematics turned inside out: The intensive faculty versus the extensive faculty. Higher Education 61(6): 693-720.
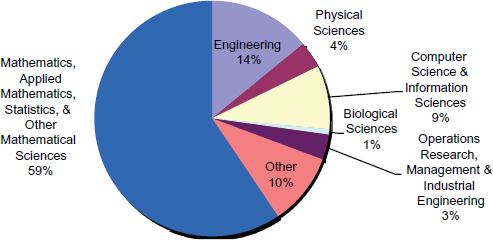
FIGURE 3-3 SIAM members identify the primary department with which they are affiliated. This figure shows the fraction of 6,269 nonstudent members identifying with a particular category.
That analysis also created a Venn diagram, reproduced here as Figure 3-4, that is helpful for envisioning how the range of mathematical science research areas map onto an intellectual space that is broader than that covered by most academic mathematics departments. (The diagram also shows how the teaching foci of mathematics and nonmathematics departments differ from their research foci.)
IMPLICATIONS OF THE BROADENING OF THE MATHEMATICAL SCIENCES
The tremendous growth in the ways in which the mathematical sciences are being used stretches the mathematical science enterprise—its people, teaching, and research breadth. If our overall research enterprise is operating well, the researchers who traditionally call themselves mathematical scientists—the central ellipse in Figure 3-2—are in turn stimulated by the challenges from the frontiers, where new types of phenomena or data stimulate fresh thinking about mathematical and statistical modeling and new technical challenges stimulate deeper questions for the mathematical sciences.
______________________
6 Some of those 75,000 papers are attributable to researchers in departments of statistics or operations research, which we would clearly count as being in the central disk of Figure 3-2. But the cited paper notes that only about 17 percent of the research indexed by Zentralblatt MATH is classified as dealing with statistics, probability, or operations research.
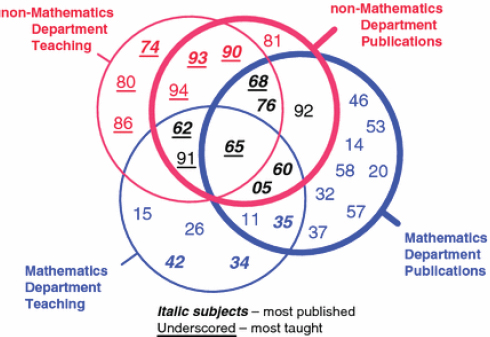
FIGURE 3-4 Representation of the research and teaching span of top mathematics departments and of nonmathematics departments in the same academic institutions. Subjects most published are shown in italics; subjects most taught are underscored. SOURCE: Joseph Grcar, 2011, Mathematics turned inside out: The intensive faculty versus the extensive faculty. Higher Education 61(6):693-720, Figure 8. The numbers correspond to the following Zentralblatt MATH classifications:
05 Combinatorics
11 Number theory
14 Algebraic geometry
15 Linear, multilinear algebra
20 Group theory
26 Real functions
32 Several complex variables
34 Ordinary differential equations
35 Partial differential equations
37 Dynamical systems
42 Fourier analysis
46 Functional analysis
53 Differential geometry
57 Manifolds, cell complexes
58 Global analysis
60 Probability theory
62 Statistics
65 Numerical analysis
68 Computer science
74 Mechanics of deformable solids
76 Fluid mechanics
80 Classical thermodynamics
81 Quantum theory
86 Geophysics
90 Operations research
91 Game theory, economics
92 Biology
93 Systems theory, control
94 Information and communications
Many people with mathematical sciences training who now work at those frontiers—operations research, computer science, engineering, economics, and so on—have told the committee that they appreciate the grounding provided by their mathematical science backgrounds and that, to them, it is natural and healthy to consider the entire family tree as being a unified whole. Many mathematical scientists and academic math departments have justifiably focused on core areas, and this is natural in the sense that no other community has a mandate to ensure that the core areas remain strong and robust. But it is essential that there be an easy flow of concepts, results, methods, and people across the entirety of the mathematical sciences. For that reason, it is essential that the mathematical sciences community actively embraces the broad community of researchers who contribute intellectually to the mathematical sciences, including people who are professionally associated with another discipline.
Anecdotal information suggests that the number of graduate students receiving training in both mathematics and another field—from biology to engineering—has increased dramatically in recent years. This trend is recognized and encouraged, for example, by the Simons Foundation’s Math+X program, which provides cross-disciplinary professorships and support for graduate students and postdoctoral researchers who straddle two fields. If this phenomenon is as general as the committee believes it to be, it shows how mathematic sciences graduate education is contributing to science and engineering generally and also how the interest in interfaces is growing. In order for the community to rationally govern itself, and for funding agencies to properly target their resources, it is necessary to begin gathering data on this trend.
Recommendation 3-1: The National Science Foundation should systematically gather data on such interactions—for example, by surveying departments in the mathematical sciences for the number of enrollments in graduate courses by students from other disciplines, as well as the number of enrollments of graduate students in the mathematical sciences in courses outside the mathematical sciences. The most effective way to gather these data might be to ask the American Society to extend its annual questionnaires to include such queries.
Program officers in NSF/DMS and in other funding agencies are aware of many overlaps between the mathematical sciences and other disciplines,
and there are many examples of flexibility in funding—mathematical scientists funded by units that primarily focus on other disciplines, and vice versa. DMS in particular works to varying degrees with other NSF units, through formal mechanisms such as shared funding programs and informal mechanisms such as program officers redirecting proposals from one division to another, divisions helping one another in identifying reviewers, and so on. Again, for the mathematical sciences community to have a more complete understanding of its reach, and to help funding agencies best target their programs, the committee recommends that a modest amount of data be collected more methodically.
Recommendation 3-2: The National Science Foundation should assemble data about the degree to which research with a mathematical science character is supported elsewhere in the Foundation. (Such an analysis would be of greatest value if it were performed at a level above DMS.) A study aimed at developing this insight with respect to statistical sciences within NSF is under way as this is written, at the request of the NSF assistant director for mathematics and physical sciences. A broader such study would help the mathematical sciences community better understand its current reach, and it could help DMS position its own portfolio to best complement other sources of support for the broader mathematical sciences enterprise. It would provide a baseline for identifying changes in that enterprise over time. Other agencies and foundations that support the mathematical sciences would benefit from a similar self-evaluation.
Data collected in response to Recommendations 3-1 and 3-2 can help the community, perhaps through its professional societies, adjust graduate training to better reflect actual student behavior. For example, if a significant fraction of mathematics graduate students take courses outside of mathematics, either out of interest or concern about future opportunities, this is something mathematics departments need to know about and respond to. Similarly, a junior faculty member in an interdisciplinary field would benefit by knowing which NSF divisions have funded work in their field. While such knowledge can often be found through targeted conversation, seeing the complete picture would be beneficial for individual researchers, and it might alter the way the mathematical sciences community sees itself.
In a discussion with industry leaders recounted in Chapter 5, the committee was struck by the scale of the demand for workers with mathematical science skills at all degree levels, regardless of their field of training. It heard about the growing demand for people with skills in data analytics, the continuing need for mathematical science skills in the financial sector,
and many novel challenges for mathematical scientists working for Internet-driven corporations and throughout the entertainment and gaming sector. There is a burgeoning job market based on mathematical science skills. However, only a small fraction of the people hired by those industry leaders actually hold degrees in mathematics and statistics; these slots are often filled by individuals with training in computer science, engineering, or physical science. While those backgrounds appear to be acceptable to employers, this explosion of jobs based on mathematical science skills represents a great opportunity for the mathematical sciences, and it should stimulate the community in three ways:
• These growing areas of application bring associated research challenges. This is already well recognized in the areas of search technology, financial mathematics, machine learning, and data analytics. No doubt new research challenges will continue to feed back to the mathematical sciences research community as new applications mature;
• The demand for people with appropriate skills will be felt by mathematical science educators, who play a major role in teaching those skills to students in a variety of fields; and
• The large number of career paths now based in the mathematical sciences calls for changes in the curricula for mathematics and statistics undergraduates and graduate students. This will be discussed in the next chapter.
This striking growth in the need for mathematical skills in and for people who might be called “mathematical science practitioners,” people with cutting-edge knowledge but who may not be focused on research—presents a great opportunity for the mathematical sciences community. In the past, training in the mathematical sciences was of course essential to the education of researchers in mathematics, statistics, and many fields of science and engineering. And an undergraduate major in mathematics or statistics was always a good basic degree, a stepping-stone to many careers. But the mathematical sciences community tends to view itself as consisting primarily of mathematical science researchers and educators and not extending more broadly. As more people trained in the mathematical sciences at all levels continue in careers that rely on mathematical sciences research, there is an opportunity for the mathematical sciences community to embrace new classes of professionals. At a number of universities, there are opportunities for undergraduate students to engage in research in nonacademic settings and internship programs for graduate students at national laboratories and industry. Some opportunities at both the postdoctoral and more senior levels are available at national laboratories
and government agencies. It would be a welcome development for opportunities of this kind to be expanded at all levels. Experiences of this kind at the faculty level can be especially valuable.
In an ideal world, the mathematical sciences community would have a clearer understanding of its scale and impacts. In addition to the steps identified in Recommendations 3-1 and 3-2, annual collection of the following information would allow the community to better understand and improve itself:
• A compilation of important new technology areas, patents, and business start-ups that have applied results from the mathematical sciences, and estimates of employment related to these developments;
• A compilation of existing technology areas that require input and training from the mathematical sciences community, and estimates of employment related to these areas;
• A compilation of new undergraduate and/or graduate programs with significant mathematical science content;
• The ratio of the number of jobs with significant mathematical science content to the number of new graduates (at different levels) in the mathematical sciences;
• An analysis of current employment of people who received federal research or training support in the past, to determine whether they are now in U.S. universities, foreign universities, U.S. or foreign industry, U.S. or foreign government, military, and so on;
• A compilation and analysis of collaborations involving mathematical scientists.
Perhaps the mathematical science professional societies, in concert with some funding agencies, could work to build up such an information base, which would help the enterprise move forward. However, the committee is well aware of the challenges in gathering such data, which would very likely be imprecise and incomplete.
TWO MAJOR DRIVERS OF EXPANSION: COMPUTATION AND BIG DATA
Two factors have combined to spark the enormous expansion of the role of the mathematical sciences: (1) the widespread availability of computing power and the consequent reliance on simulation via mathematical models by so much of today’s science, engineering, and technology and (2) the explosion in the amount of data being collected or generated, which often is of a scale that it can only be evaluated through mathematical and statistical techniques. As a result, the two areas of computation and “big
data” have emerged as major drivers of mathematical research and the broadening of the enterprise. Needless to say, these are deeply intertwined, and it is becoming increasingly standard for major research efforts to require expertise in both simulation and large-scale data analysis.
Before discussing these two major drivers, it is critical to point out that a great deal of mathematical sciences research continues to be driven by the internal logic of the subject—that is, initiated by individual researchers in response to their best understanding of promising directions. (The often-used phrase “curiosity driven” understates the tremendous effectiveness of this approach over centuries.) In the committee’s conversations with many mathematical scientists, it frequently heard the opinion that it is impossible to predict particular research areas in which important new developments are likely to occur. While over the years there have been important shifts in the level of activity in certain subjects—for example, the growing significance of probabilistic methods, the rise of discrete mathematics, and the growing use of Bayesian statistics—the committee did not attempt to exhaustively survey such changes or prognosticate about the subjects that are most likely to produce relevant breakthroughs. The principal lesson is that it continues to be important for funding sources to support excellence wherever it is found and to continue to support the full range of mathematical sciences research.
A new Canadian study on the long-range plan for that country’s mathematics and statistics reached a similar conclusion, explaining it as follows:
[I]t is difficult to predict which particular fields of mathematics and statistics will most guide innovation in the next decades. Indeed, all areas of the mathematical and statistical sciences have the potential to be important to innovation, but the time scale may be very long, and the nature of the link is likely to be surprising. Many areas of the mathematical and statistical sciences that strike us now as abstract and removed from obvious application will be useful in ways that we cannot currently imagine. . . . On the one hand, we need a research landscape that is flexible and non-prescriptive in terms of areas to be supported. We must have a research funding landscape capable of nurturing a broad range of basic and applied research and that can take into account the changing characteristics of the research enterprise itself. And on the other hand, we need to build and maintain infrastructure that will connect the mathematical and statistical sciences to strategic growth areas . . . and will encourage effective technology transfer and innovation across science, industry and society.7
Computation
______________________
7 “Solutions for a Complex Age: Long Range Plan for Mathematical & Statistical Sciences Research in Canada,” Natural Sciences & Engineering Research Council (Canada), 2012. Accessed from http://longrangeplan.ca/wp-content/uploads/2012/12/3107_MATH_LRP-1212-web.pdf, January 28, 2013. Quoted text is from p. 24.
As science, engineering, government, and business rely increasingly on complex computational simulations, it is inevitable that connections between those sectors and the mathematical sciences are strengthened. That is because computational modeling is inherently mathematical. Accordingly, those fields depend on—and profit from—advances in the mathematical sciences and the maintainance of a healthy mathematical science enterprise. The same is true to the extent that those sectors increasingly rely on the analysis of large-scale quantities of data.
This is not to say that a mathematical scientist is needed whenever someone builds or exercises a computer simulation or analyzes data (although the involvement of a mathematical scientist is often beneficial when the work is novel or complex). But it is true that more and more scientists, engineers, and business people require or benefit from higher-level course work in the mathematical sciences, which strengthens connections between disciplines. And it is also true that the complexity of phenomena that can now be simulated in silico, and the complexity of analyses made possible by terascale data, are pushing research frontiers in the mathematical sciences and challenging those who could have previously learned the necessary skills as they carry out their primary tasks. As this complexity increases, we are finding more and more occasions where specialized mathematical and statistical experience is required or would be beneficial.
Some readers may assume that many of the topics mentioned in this chapter fall in the domain of computer science rather than the mathematical sciences. In fact, many of these areas of inquiry straddle both fields or could be labeled either way. For example, the process of searching data, whether in a database or on the Internet, requires both the products of computer science research and modeling and analysis tools from the mathematical sciences. The challenges of theoretical computer science itself are in fact quite mathematical, and the fields of scientific computing and machine learning sit squarely at the interface of the mathematical sciences and computer science (with insight from the domain of application, in many cases). Indeed, most modeling, simulation, and analysis is built on the output of both disciplines, and researchers with very similar backgrounds can be found in academic departments of mathematics, statistics, or computer science. There is, of course, a great deal of mathematical sciences research that has not that much in common with computer sciences research—and, likewise, a great deal of computer science research that is not particularly close to the mathematical sciences.
Because so many people across science, engineering, and medicine now learn some mathematics and/or statistics, some ask why we need people who specialize in the mathematical sciences to be involved in inter
disciplinary teams. The reason is that mathematical science researchers not only create the tools that are translated into applications elsewhere, but they are also the creative partners who can adapt mathematical sciences results appropriately for different problems. This latter sort of collaboration can result in breakthrough capabilities well worth the investment of time that is sometimes associated with establishing a cross-disciplinary team. It is not always enough to rely on the mathematics and statistics that is captured in textbooks or software, for two reasons: (1) progress is continually being made, and off-the-shelf techniques are unlikely to be cutting edge, and (2) solutions tailored to particular situations or questions can often be much more effective than more generic approaches. These are the benefits to the nonmathematical sciences members of the team. For mathematical science collaborators, the benefits are likewise dual: (1) fresh challenges are uncovered that may stimulate new results of intrinsic importance to the mathematical sciences and (2) their mathematical science techniques and insights can have wider impact.
In application areas with well-established mathematical models for phenomena of interest—such as physics and engineering—researchers are able to use the great advances in computing and data collection of recent decades to investigate more complex phenomena and undertake more precise analyses. Conversely, where mathematical models are lacking, the growth in computing power and data now allow for computational simulations using alternative models and for empirically generated relationships as means of investigation.
Computational simulation now guides researchers in deciding which experiments to perform, how to interpret experimental results, which prototypes to build, which medical treatments might work, and so on. Indeed, the ability to simulate a phenomenon is often regarded as a test of our ability to understand it. Over the past 10-15 years, computational capabilities reached a threshold at which statistical methods such as Markov chain Monte Carlo methods and large-scale data mining and analysis became feasible, and these methods have proved to be of great value in a wide range of situations.
For example, at one of its meetings the study committee saw a simulation of biochemical activity developed by Terrence Sejnowski of the Salk Institute for Biological Studies. It was a tour de force of computational simulation—based on cutting-edge mathematical sciences and computer science—that would not have been feasible until recently and that enables novel investigations into complex biological phenomena. As another example, over the past 30 years or so, ultrasound has progressed from providing still images to dynamically showing a beating heart and, more recently, to showing the evolution of a full baby in the womb. The mathematical basis for ultrasound requires solving inverse problems and draws
from techniques and results in pure mathematical analysis, in the theory of wave propagation in fluids and elastic media, and in more practical areas such as fast numerical methods and image processing. As ultrasound technologies have improved, new mathematical challenges also need to be addressed.
A recent paper prepared for the Advisory Committee for NSF’s Mathematics and Physical Sciences (MPS) Directorate identifies the following five “core elements” that underpin computational science and engineering:8
(i) the development and long-term stewardship of software, including new and “staple” community codes, open source codes, and codes for new or nonconventional architectures;
(ii) the development of models, algorithms, and tools and techniques for verification, validation and uncertainty quantification;
(iii) the development of tools, techniques, and best practices for ultra large data sets;
(iv) the development and adoption of cyber tools for collaboration, sharing, re-use and re-purposing of software and data by MPS communities; and
(v) education, training and workforce development of the next generation of computational scientists.
The mathematical sciences contribute in essential ways to all the items on this list except the fourth.
The great majority of computational science and engineering can be carried out well by investigators from the field of study: They know how to create a mathematical model of the phenomenon under study, and standard numerical solution tools are adequate. Even in these cases, though, some specialized mathematical insights might be required—such as knowing how and when to add “artificial viscosity” to a representation of fluid flow, or how to handle “stiffness” in sets of ordinary differential equations—but that degree of skill has spread among numerical modelers in many disciplines. However, as the phenomena being modeled become increasingly complex, perhaps requiring specialized articulation between models at different scales and of different mathematical types, specialized mathematical science skills become more and more important. Absent such skills and experience, computational models can be unstable or even produce unreliable results. Validation of such complex models requires very specialized experience, and the critical task of quantifying their uncertainties can be
______________________
8 Sharon Glotzer, David Keyes, Joel Tohline, and Jerzy Leszczynski, “Computational Science.” May 14, 2010. Available at http://www.nsf.gov/attachments/118651/public/Computational_Science_White_Paper.pdf.
very challenging.9 And when models are developed empirically by finding patterns in large-scale data—which is becoming ever more common—there are many opportunities for spurious associations. The research teams must have strong statistical skills in order to create reliable knowledge in such cases.
In response to the need to harness this vast computational power, the community of mathematical scientists who are experts in scientific computation continues to expand. This cadre of researchers develops improved solution methods, algorithms for gridding schemes and computational graphics, and so on. Much more of that work will be stimulated by new computer architectures now emerging. And, a much broader range of mathematical science challenges stem from this trend. The theory of differential equations, for example, is challenged to provide structures that enable us to analyze approximations to multiscale models; stronger methods of model validation are needed; algorithms need to be developed and characterized; theoretical questions in computer science need resolution; and so on. Though often simply called “software,” the steps to represent reality on a computer pose a large number of challenges for the mathematical sciences.10
A prime example of how expanding computational and data resources have led to the “mathematization” of a field of science is the way that biology became much more quantitative and dependent on mathematical and statistical modeling following the emergence of genomics. High-throughput data in biology has been an important driver for new statistical research over the past 10-15 years. Research in genomics and proteomics relies heavily on the mathematical sciences, often in challenging ways, and of disease, evolution, agriculture, and other topics have consequently become quantitative as genomic and proteomic information is incorporated as a foundation for research. Arguably, this development has placed statisticians as central players in one of the hottest fields of science. Over the next 10-15 years, acquiring genomic data will become fairly straightforward, and increasingly it will be available to illuminate biological processes. A
______________________
9 See Kristin Sainani, 2011, Error!–What biomedical computing can learn from its mistakes. Biomedical Computation Review, September 1, gives an overview of sources of error and points to some striking published studies. Available at http://biomedicalcomputationreview.org/content/error-%E2%80%93-what-biomedical-computing-can-learn-its-mistakes. See also National Research Council, 2012. Assessing the Reliability of Complex Models: Mathematical and Statistical Foundations of Verification, Validation, and Uncertainty Quantification. The National Academies Press, Washington, D.C.
10 The full range of mathematical sciences challenges associated with advanced computing for science and engineering is discussed in Chapter 6 of NRC, 2008, The Potential Impact of High-End Capacity Computing on Four Illustrative Fields of Science and Engineering, The National Academies Press, Washington, D.C.
lot of that work depends on insights from statistics, but mathematics also provides foundations: For example, graph theoretic methods are essential in evolutionary biology; new algorithms from discrete mathematics and computer science play essential roles in search, comparison, and knowledge extraction; dynamical systems theory plays an important role in ecology; and more traditional applied mathematics is commonly used in computational neuroscience and systems biology. As biology transitions from a descriptive science to a quantitative science, the mathematical sciences will play an enormous role.
To different degrees, the social sciences are also embracing the tools of the mathematical sciences, especially statistics, data analytics, and mathematics embedded in simulations. For example, statistical models of disease transmission have provided very valuable insights about patterns and pathways. Business, especially finance and marketing, is increasingly dependent on methods from the mathematical sciences. Some topics in the humanities have also benefited from mathematical science methods, primarily data mining, data analysis, and the emerging science of networks.
The mathematical sciences are increasingly contributing to data-driven decision making in health care. Operations research is being applied to model the processes of health care delivery so they can be methodically improved. The applications use different forms of simulation, discrete optimization, Markov decision processes, dynamic programming, network modeling, and stochastic control. As health care practices move to electronic health care records, enormous amounts of data are becoming available and in need of analysis; new methods are needed because these data are not the result of controlled trials. The new field of comparative effectiveness research, which relies a great deal on statistics, aims to build on data of that sort to characterize the effectiveness of various medical interventions and their value to particular classes of patients.
“Big Data”
Embedded in several places in this discussion is the observation that data volumes are exploding, placing commensurate demands on the mathematical sciences. This prospect has been mentioned in a large number of previous reports about the discipline, but it has become very real in the past 15 years or so. A sign that this area has come of age is the unveiling in March 2012 by the White House Office of Science and Technology Policy (OSTP) of the Big Data Research and Development Initiative. OSTP Director John Holdren said pointedly that “it’s not the data per se that create value. What really matters is our ability to derive from them new insights, to recognize relationships, to make increasingly accurate predictions. Our ability, that is, to move from data, to knowledge, to action.” It is precisely
in the realm of moving from raw data via analysis to knowledge that the mathematical sciences are essential. Large, complex data sets and data streams play a significant role in stimulating new research applications across the mathematical sciences, and mathematical science advances are necessary to exploit the value in these data.
However, the role of the mathematical sciences in this area is not always recognized. Indeed, the stated goals for the OSTP initiative,
to advance state-of the-art core technologies needed to collect, store, preserve, manage, analyze, and share huge quantities of data; harness these technologies to accelerate the pace of discovery in science and engineering; strengthen our national security; and transform teaching and learning; and to expand the workforce needed to develop and use Big Data technologies,
seem to understate the amount of intellectual effort necessary to actually enable the move from data, to knowledge, to action.
Multiple issues of fundamental methodology arise in the context of large data sets. Some arise from the basic issue of scalability—that techniques developed for small or moderate-sized data sets do not translate to modern massive data sets—or from problems of data streaming, where the data set is changing while the analysis goes on. Typical questions include how to increase the signal-to-noise ratio in the recorded data, how to detect a new or different state quickly (anomaly detection), algorithmic/data structure solutions that allow fast computation of familiar statistics, hardware solutions that allow efficient or parallel computations. Data that are high-dimensional pose new challenges: New paradigms of statistical inference arise from the exploratory nature of understanding large complex data sets, and issues arise of how best to model the processes by which large, complex data sets are formed. Not all data are numerical—some are categorical, some are qualitative, and so on—and mathematical scientists contribute perspectives and techniques for dealing with both numerical and non-numerical data, and with their uncertainties. Noise in the data-gathering process needs to be modeled and then—where possible—minimized; a new algorithm can be as powerful an enhancement to resolution as a new instrument. Often, the data that can be measured are not the data that one ultimately wants. This results in what is known as an inverse problem—the process of collecting data has imposed a very complicated transformation on the data one wants, and a computational algorithm is needed to invert the process. The classic example is radar, where the shape of an object is reconstructed from how radio waves bounce off it. Simplifying the data so as to find its underlying structure is usually essential in large data sets. The general goal of dimensionality reduction—taking data with a large number of measurements and finding which combinations of the measurements are
sufficient to embody the essential features of the data set—is pervasive. Various methods with their roots in linear algebra and statistics are used and continually being improved, and increasingly deep results from real analysis and probabilistic methods—such as random projections and diffusion geometry—are being brought to bear.
Statisticians contribute a long history of experience in dealing with the intricacies of real-world data—how to detect when something is going wrong with the data-gathering process, how to distinguish between outliers that are important and outliers that come from measurement error, how to design the data-gathering process so as to maximize the value of the data collected, how to cleanse the data of inevitable errors and gaps. As data sets grow into the terabyte and petabyte range, existing statistical tools may no longer suffice, and continuing innovation is necessary. In the realm of massive data, long-standing paradigms can break—for example, false positives can become the norm rather than the exception—and more research endeavors need strong statistical expertise.
For example, in a large portion of data-intensive problems, observations are abundant and the challenge is not so much how to avoid being deceived by a small sample size as to be able to detect relevant patterns. As noted in the New York Times: “In field after field, computing and the Web are creating new realms of data to explore sensor signals, surveillance tapes, social network chatter, public records and more.”11 This may call for researchers in machine or statistical learning to develop algorithms that predict an outcome based on empirical data, such as sensor data or streams from the Internet. In that approach, one uses a sample of the data to discover relationships between a quantity of interest and explanatory variables. Strong mathematical scientists who work in this area combine best practices in data modeling, uncertainty management, and statistics, with insight about the application area and the computing implementation. These prediction problems arise everywhere: in finance and medicine, of course, but they are also crucial to the modern economy so much so that businesses like Netflix, Google, and Facebook rely on progress in this area. A recent trend is that statistics graduate students who in the past often ended up in pharmaceutical companies, where they would design clinical trials, are increasingly also being recruited by companies focused on Internet commerce.
Finding what one is looking for in a vast sea of data depends on search algorithms. This is an expanding subject, because these algorithms need to search a database where the data may include words, numbers, images and video, sounds, answers to questionnaires, and other types of data, all linked
______________________
11 Steve Lohr, 2009, For today’s graduate, just one word: Statistics. New York Times, August 5.
together in various ways. It is also necessary for these methods to become increasingly “intelligent” as the scale of the data increases, because it is insufficient to simply identify matches and propose an ordered list of hits. New techniques of machine learning continue to be developed to address this need. Another new consideration is that data often come in the form of a network; performing mathematical and statistical analyses on networks requires new methods.
Statistical decision theory is the branch of statistics specifically devoted to using data to enable optimal decisions. What it adds to classical statistics beyond inference of probabilities is that it integrates into the decision information about costs and the value of various outcomes. It is critical to many of the projects envisioned in OSTP’s Big Data initiative. To pick two examples from many,12 the Center for Medicare and Medicaid Services (CMS) has the program Using Administrative Claims Data (Medicare) to Improve Decision-Making while the Food and Drug Administration is establishing the Virtual Laboratory Environment, which will apply “advanced analytical and statistical tools and capabilities, crowd-sourcing of analytics to predict and promote public health.” Better decision making has been singled out as one of the most promising ways to curtail rising medical costs while optimizing patient outcomes, and statistics is at the heart of this issue.
Ideas from statistics, theoretical computer science, and mathematics have provided a growing arsenal of methods for machine learning and statistical learning theory: principal component analysis, nearest neighbor techniques, support vector machines, Bayesian and sensor networks, regularized learning, reinforcement learning, sparse estimation, neural networks, kernel methods, tree-based methods, the bootstrap, boosting, association rules, hidden Markov models, and independent component analysis—and the list keeps growing. This is a field where new ideas are introduced in rapid-fire succession, where the effectiveness of new methods often is markedly greater than existing ones, and where new classes of problems appear frequently.
Large data sets require a high level of computational sophistication because operations that are easy at a small scale—such as moving data between machines or in and out of storage, visualizing the data, or displaying results—can all require substantial algorithmic ingenuity. As a data set becomes increasingly massive, it may be infeasible to gather it in one place and analyze it as a whole. Thus, there may be a need for algorithms that operate in a distributed fashion, analyzing subsets of the data and aggregating those results to understand the complete set. One aspect of this is the
______________________
12 The information and quotation here are drawn from OSTP, “Fact Sheet: Big Data Across the Federal Government, March 29, 2012.” Available at http://www.whitehouse.gov/sites/default/files/microsites/ostp/big_data_fact_sheet_final.pdf.
challenge of data assimilation, in which we wish to use new data to update model parameters without reanalyzing the entire data set. This is essential when new waves of data continue to arrive, or subsets are analyzed in isolation of one another, and one aims to improve the model and inferences in an adaptive fashion—for example, with streaming algorithms. The mathematical sciences contribute in important ways to the development of new algorithms and methods of analysis, as do other areas as well.
Simplifying the data so as to find their underlying structure is usually essential in large data sets. The general goal of dimensionality taking data with a large number of measurements and finding which combinations of the measurements are sufficient to embody the essential features of the data set—is pervasive. Various methods with their roots in linear algebra, statistics, and, increasingly, deep results from real analysis and probabilistic methods—such as random projections and diffusion geometry—are used in different circumstances, and improvements are still needed. Such issues are central to NSF’s Core Techniques and Technologies for Advancing Big Data Science and Engineering program and to data as diverse as those from climate, genomics, and threat reduction. Related to search and also to dimensionality reduction is the issue of anomaly detection—detecting which changes in a large system are abnormal or dangerous, often characterized as the needle-in-a-haystack problem. The Defense Advanced Research Projects Agency (DARPA) has its Anomaly Detection at Multiple Scales program on anomaly-detection and characterization in massive data sets, with a particular focus on insider-threat detection, in which anomalous actions by an individual are detected against a background of routine network activity. A wide range of statistical and machine learning techniques can be brought to bear on this, some growing out of statistical techniques originally used for quality control, others pioneered by mathematicians in detecting credit card fraud.
Two types of data that are extraordinarily important yet exceptionally subtle to analyze are words and images. The fields of text mining and natural language processing deal with finding and extracting information and knowledge from a variety of textual sources, and creating probabilistic models of how language and grammatical structures are generated. Image processing, machine vision, and image analysis attempt to restore noisy image data into a form that can be processed by the human eye, or to bypass the human eye altogether and understand and represent within a computer what is going on in an image without human intervention.
Related to image analysis is the problem of finding an appropriate language for describing shape. Multiple approaches, from level sets to “eigenshapes,” come in, with differential geometry playing a central role. As part of this problem, methods are needed to describe small deformations of shapes, usually using some aspect of the geometry of the space of
diffeomorphisms. Shape analysis also comes into play in virtual surgery, where surgical outcomes are simulated on the computer before being tried on a patient, and in remote surgery for the battlefield. Here one needs to combine mathematical modeling techniques based on the differential equations describing tissue mechanics with shape description and visualization methods.
As our society is learning somewhat painfully, data must be protected. The need for privacy and security has given rise to the areas of privacy-preserving data mining and encrypted computation, where one wishes to be able to analyze a data set without compromising privacy, and to be able to do computations on an encrypted data set while it remains encrypted.
CONTRIBUTIONS OF MATHEMATICAL SCIENCES TO SCIENCE AND ENGINEERING
The mathematical sciences have a long history of interaction with other fields of science and engineering. This interaction provides tools and insights to help those other fields advance; at the same time, the efforts of those fields to push research frontiers routinely raise new challenges for the mathematical sciences themselves. One way of evaluating the state of the mathematical sciences is to examine the richness of this interplay. Some of the interactions between mathematics and physics are described in Chapter 2, but the range extends well beyond physics. A compelling illustration of how much other fields rely on the mathematical sciences arises from examining those fields’ own assessments of promising directions and identifying the directions that are dependent on parallel progress in the mathematical sciences. A number of such illustrations have been collected in Appendix D.
CONTRIBUTIONS OF MATHEMATICAL SCIENCES TO INDUSTRY
The role of the mathematical sciences in industry has a long history, going back to the days when the Egyptians used the 3-4-5 right triangle to restore boundaries of farms after the annual flooding of the Nile. That said, the recent period is one of remarkable growth and diversification. Even in old-line industries, the role of the mathematical sciences has expanded. For example, whereas the aviation industry has long used mathematics in the design of airplane wings and statistics in ensuring quality control in production, now the mathematical sciences are also crucial to GPS and navigation systems, to simulating the structural soundness of a design, and to optimizing the flow of production. Instead of being used just to streamline cars and model traffic flows, the mathematical sciences are also involved in the latest developments, such as design of automated vehicle detection and
avoidance systems that may one day lead to automated driving. Whereas statistics has long been a key element of medical trials, now the mathematical sciences are involved in drug design and in modeling new ways for drugs to be delivered to tumors, and they will be essential in making inferences in circumstances that do not allow double-blind, randomized clinical trials. The financial sector, which once relied on statistics to design portfolios that minimized risk for a given level of return, now makes use of statistics, machine learning, stochastic modeling, optimization, and the new science of networks in pricing and designing securities and in assessing risk.
What is most striking, however, is the number of new industries that the mathematical sciences are a part of, often as a key enabler. The encryption industry makes use of number theory to make Internet commerce possible. The “search” industry relies on ideas from the mathematical sciences to make the Internet’s vast resources of information searchable. The social networking industry makes use of graph theory and machine learning. The animation and computer game industry makes use of techniques as diverse as differential geometry and partial differential equations. The biotech industry heavily uses the mathematical sciences in modeling the action of drugs, searching genomes for genes relevant to human disease or relevant to bioengineered organisms, and discovering new drugs and understanding how they might act. The imaging industry uses ideas from differential geometry and signal processing to procure minimally invasive medical and industrial images and, within medicine, adds methods from inverse problems to design targeted radiation therapies and is moving to incorporate the new field of computational anatomy to enable remote surgery. The online advertising industry uses ideas from game theory and discrete mathematics to price and bid on online ads and methods from statistics and machine learning to decide how to target those ads. The marketing industry now employs sophisticated statistical and machine learning techniques to target customers and to choose locations for new stores. The credit card industry uses a variety of methods to detect fraud and denial-of-service attacks. Political campaigns now make use of complex models of the electorate, and election-night predictions rely on integrating these models with exit polls. The semiconductor industry uses optimization to design computer chips and in simulating the manufacture and behavior of designer materials. The mathematical sciences are now present in almost every industry, and the range of mathematical sciences being used would have been unimaginable a generation ago.
This point is driven home by the following list of case studies assembled for the SIAM report Mathematics in Industry.13 This list is just illustrative, but its breadth is striking:
______________________
13 Society for Industrial and Applied Mathematics, 2012, Mathematics in Industry. SIAM, Philadelphia, Pa.
• Predictive analytics,
• Image analysis and data mining,
• Scheduling and routing of deliveries,
• Mathematical finance,
• Algorithmic trading,
• Systems biology,
• Molecular dynamics,
• Whole-patient models,
• Oil basin modeling,
• Virtual prototyping,
• Molecular dynamics for product engineering,
• Multidisciplinary design optimization and computer-aided design,
• Robotics,
• Supply chain management,
• Logistics,
• Cloud computing,
• Modeling complex systems,
• Viscous fluid flow for computer and television screen design,
• Infrastructure management for smart cities, and
• Computer systems, software, and information technology.
The reader is directed to the SIAM report to see the details of these case studies,14 which provide many examples of the significant and cost-effective impact of mathematical science expertise and research on innovation, economic competitiveness, and national security.
Another recent report on the mathematical sciences in industry came to the following conclusions:
It is evident that, in view of the ever-increasing complexity of real life applications, the ability to effectively use mathematical modelling, simulation, control and optimisation will be the foundation for the technological and economic development of Europe and the world.15
Only [the mathematical sciences] can help industry to optimise more and more complex systems with more and more constraints.16
However, that report also points out the following truism:
[Engineering] designers use virtual design environments that rely heavily on mathematics, and produce new products that are well recognised by
______________________
14 Ibid., pp. 9-24.
15 European Science Foundation, 2010, Mathematics and Industry. Strasbourg, France, p. 8.
16 Ibid., p. 12.
management. The major effort concerned with the construction of reliable, robust and efficient virtual design environments is, however, not recognised. As a result, mathematics is not usually considered a key technology in industry. The workaround for this problem usually consists of leaving the mathematics to specialised small companies that often build on mathematical and software solutions developed in academia. Unfortunately, the level of communication between these commercial vendors and their academic partners with industry is often at a very low level. This, in turn, leads to the observation that yesterday’s problems in industry can be solved, but not the problems of today and tomorrow. The latter can only be addressed adequately if an effort is made to drastically improve the communication between industrial designers and mathematicians.17
One way to address this communication challenge, of course, is to include high-caliber mathematical scientists within corporate R&D units.
The mathematical functions of greatest value in these and other successful applications were characterized by R&D managers in 1996 as follows:18
• Modeling and simulation,
• Mathematical formulation of problems,
• Algorithm and software development,
• Problem-solving,
• Statistical analysis,
• Verifying correctness, and
• Analysis of accuracy and reliability.
To this list, the European Science Foundation report adds optimization, noting (p. 12) that “due to the increased computational power and the achievements obtained in speed-up of algorithms . . . optimization of products has [come] into reach. This is of vital importance to industry.” This is a very important development, and it opens up new challenges for the mathematical sciences, such as how to efficiently explore design options and how to characterize the uncertainties of this computational sampling of the space.
These sorts of opportunities were implicitly recognized in a report from the Chinese Academy of Sciences (CAS), Science and Technology in China: A Roadmap to 2050.19 That report identified eight systems of importance for socioeconomic development: sustainable energy and resources,
______________________
17 Ibid., p. 9.
18 Society for Industrial and Applied Mathematics, 1996, Mathematics in Industry. Available at http://www.siam.org/reports/mii/1996/listtables.php#lt4.
19 CAS, 2010, Science & Technology in China: A Roadmap to 2050. Springer. Available online at http://www.bps.cas.cn/ztzl/cx2050/nrfb/201008/t20100804_2917262.html.
advanced materials and intelligent manufacturing, ubiquitous information networking, ecological and high-value agriculture and biological industry, health assurance, ecological and environmental conservation, space and ocean exploration, and national and public security. To support the maturation of these systems, the report goes on to identify 22 science and technology initiatives. Of these, three will build on the mathematical sciences: an initiative to create “ubiquitous informationized manufacturing system[s],” another to develop exascale computing technology, and a third in basic cross-disciplinary research in mathematics and complex systems.
The last-mentioned initiative is intended to research the “basic principles behind various kinds of complex systems,” and the report recommends that major efforts be made in the following research directions:
• Mathematical physics equations;
• Multiscale modeling and computation of complex systems;
• Machine intelligence and mathematics mechanization;
• Theories and methods for stochastic structures and data;
• Collective behaviors of multiagent complex systems, their control and intervention; and
• Complex stochastic networks, complex adaptive systems, and related areas.
In particular, the report recommends that due to the fundamental importance of complex systems, the Chinese government should provide sustained and steady support for research into such systems so as to achieve major accomplishments in this important field.
One more example of the role of the mathematical sciences in industry comes from the NRC report Visionary Manufacturing Challenges for 2020,20 which identified R&D that would be necessary to advance national capabilities in manufacturing. A number of these capabilities rely on research in modeling and simulation, control theory, and informatics:
• Ultimately, simulations of manufacturing systems would be based on a unified taxonomy for process characteristics that include human characteristics in process models. Other areas for research include a general theory for adaptive systems that could be translated into manufacturing processes, systems, and the manufacturing enterprise; tools to optimize design choices to incorporate the most affordable manufacturing approaches; and systems research on the interaction between workers and manufacturing processes for the development of adaptive, flexible controls. (p. 39)
______________________
20 NRC, 1998, Visionary Manufacturing Challenges for 2020. National Academy Press, Washington, D.C.
• Modeling and simulation capabilities for evaluating process and enterprise scenarios will be important in the development of reconfigurable enterprises. . . . Virtual prototyping of manufacturing processes and systems will enable manufacturers to evaluate a range of choices for optimizing their enterprises. Promising areas for the application of modeling and simulation technology for reconfigurable systems include neural networks for optimizing reconfiguration approaches and artificial intelligence for decision making. . . . Processes that can be adapted or readily reconfigured will require flexible sensors and control algorithms that provide precision process control of a range of processes and environments. (pp. 39-40)
• Research in enterprise modeling tools will include ‘soft’ modeling (e.g., models that consider human behavior as an element of the system and models of information flow and communications), the optimization and integration of mixed models, the optimization of hardware systems, models of organizational structures and cross-organizational behavior, and models of complex or nonlinear systems and processes. (p. 44)
• Future information systems will have to be able to collect and sift through vast amounts of information. (p. 44)
Today’s renewed emphasis on advanced manufacturing, as exemplified by the recent report Capturing Domestic Competitive Advantage in Advanced Manufacturing,21 also relies implicitly on advances in the mathematical sciences. The 11 cross-cutting technology areas identified in that report (p. 18) as top candidates for R&D investments rely in multiple ways on modeling, simulation, and analysis of complex systems, analysis of large amounts of data, control, and optimization.
CONTRIBUTIONS OF MATHEMATICAL SCIENCES TO NATIONAL SECURITY
National security is another area that relies heavily on the mathematical sciences. The National Security Agency (NSA), for example, employs roughly 1,000 mathematical scientists, although the number might be half that or twice that depending on how one defines such scientists.22 They include people with backgrounds in core and applied mathematics, probability, and statistics, but people with computer science backgrounds are not included in that count. NSA hires some 40-50 mathematicians per year, and it tries to keep that rate steady so that the mathematical sciences community
______________________
21 White House, Office of Science and Technology Policy, 2012.
22 Alfred Hales, former head of the Institute for Defense Analyses, Center for Communications Research–La Jolla, presentation to the committee in December 2010. IDA’s La Jolla center conducts research for the NSA.
knows it can depend on that level of hiring. The NSA is interested in maintaining a healthy mathematical sciences community in the United States, including a sufficient supply of well-trained U.S. citizens. Most of NSA’s mathematical sciences hiring is at the graduate level, about evenly split between the M.S. and Ph.D. levels. The agency hires across almost all fields of the mathematical sciences rather than targeting specific subfields, because no one can predict the mix of skills that will be important over an employee’s decades-long career. For example, few mathematicians would have guessed decades ago that elliptic curves would be of vital interest to NSA, and now they are an important specialty underlying cryptology.
While cryptology is explicitly dependent on mathematics, many other links exist between the mathematical sciences and national security. One example is analysis of networks (discussed in the next section), which is very important for national defense. Another is scientific computing. One of the original reasons for John von Neumann’s interest in creating one of the first computers was to be able to do the computations necessary to simulate what would happen inside a hydrogen bomb. Years later, with atmospheric and underground nuclear testing banned, the country relies once again on simulations, this time to maintain the readiness of its nuclear arsenal. Because national defense relies in part on design and manufacturing of cutting-edge equipment, it also relies on the mathematical sciences through their contributions to advanced engineering and manufacturing. The level of sophistication of these tools has ratcheted steadily upward. The mathematical sciences are also essential to logistics, simulations used for training and testing, war-gaming, image and signal analysis, control of satellites and aircraft, and test and evaluation of new equipment. Figure 3-5, reproduced from Fueling Innovation and Discovery: The Mathematical Sciences in the 21st Century,23 captures the broad range of ways in which the mathematical sciences contribute to national defense.
New devices, on and off the battlefield, have come on stream and furnish dizzying quantities of data, more than can currently be analyzed. Devising ways to automate the analysis of these data is a highly mathematical and statistical challenge. Can a computer be taught to make sense of a satellite image, detecting buildings and roads and noticing when there has been a major change in the image of a site that is not due to seasonal variation? How can one make use of hyperspectral data, which measure light reflected in all frequencies of the spectrum, in order to detect the smoke plume from a chemical weapons factory? Can one identify enemy vehicles and ships in a cluttered environment? These questions and many others are inherently dependent on advances in the mathematical sciences.
______________________
23 National Research Council, 2012. The National Academies Press, Washington, D.C.
A very serious threat that did not exist in earlier days is that crucial networks are constantly subject to sophisticated attacks by thieves, mischief-makers, and hackers of unknown origin. Adaptive techniques based on the mathematical sciences are essential for reliable detection and prevention of such attacks, which grow in sophistication to elude every new strategy for preventing them.
The Department of Defense has adopted seven current priority areas for science and technology investment to benefit national security.
1. Data to decisions. Science and applications to reduce the cycle time and manpower requirements for analysis and use of large data sets.
2. Engineered resilient systems. Engineering concepts, science, and design tools to protect against malicious compromise of weapon systems and to develop agile manufacturing for trusted and assured defense systems.
3. Cyber science and technology. Science and technology for efficient, effective cyber capabilities across the spectrum of joint operations.
4. Electronic warfare/electronic protection. New concepts and technology to protect systems and extend capabilities across the electro-magnetic spectrum.
5. Countering weapons of mass destruction (WMD): Advances in DOD’s ability to locate, secure, monitor, tag, track, interdict, eliminate, and attribute WMD weapons and materials.
6. Autonomy. Science and technology to achieve autonomous systems that reliably and safely accomplish complex tasks in all environments.
7. Human systems. Science and technology to enhance human-machine interfaces, increasing productivity and effectiveness across a broad range of missions.24
While the mathematical sciences are clearly of importance to the first and third of these priority areas, they also have key roles to play in support of all of the others. Advances in the mathematical sciences that allow simulation-based design, testing, and control of complex systems are essential for creating resilient systems. Improved methods of signal analysis and processing, such as faster algorithms and more sensitive schemes for pattern recognition, are needed to advance electronic warfare and protection. Rapidly developing tools for analyzing social networks, which are based on novel methods of statistical analysis of networks, are being applied in order
______________________
24 Department of Defense, 2012, Memorandum on Science and Technology (S&T) Priorities for Fiscal Years 2013·17 Planning. Available at http://acq.osd.mil/chieftechnologist/publications/docs/OSD%2002073-11.pdf. Accessed May 3, 2012.
to improve our capabilities in counter-WMD. And mathematical science methods of machine learning are necessary for improving our capabilities in autonomy and human-machine interfaces. Computational neuroscience, which relies heavily on the mathematical sciences, is also a promising area for future developments in human-machine interfaces.
The realm of threat detection in general requires a multiplicity of techniques from the mathematical sciences. How can one most quickly detect patterns that might indicate the spread of a pathogen spread by bioterrorism? How does one understand the structure of a terrorist network? Can one design a power grid or a transportation network in such a way that it is maximally resistant to attack? A new threat, cyberwarfare, grows in magnitude. Fighting back will involve a multipronged response: better encryption, optimized design of networks, and the burgeoning mathematics-and statistics-intensive field of anomaly detection.





































