2
Potential Value of a Digital Mathematics Library
WHAT IS MISSING FROM THE MATHEMATICAL INFORMATION LANDSCAPE?
The current mathematical information landscape is complex and diverse, as described in Chapter 1 and Appendix C. Current digital mathematical resources provide services such as electronic access to papers (often with advanced features capable of searching and sorting based on key words, subject areas, text searches, and authors), platforms for discussion, and improved navigation across multiple data sources. What they do not do is allow a user to systematically explore the information captured within the literature and forums and readily explore connections that may not be obvious from looking at the material alone.
This inability to easily explore the mathematical ideas that exist within a mathematical paper, which cannot easily be searched for, is a detriment to the mathematical community. There is a largely unexplored network of information embedded in the connections of mathematical objects, and formalizing this network—making it easy to see, manipulate, and explore—holds the potential to vastly accelerate and expand currently mathematical research. This network would consist of information from traditional resources, such as research papers published in journals, and content dispersed in other Internet-based resources and databases. Initial development of the DML could begin immediately with the aim of providing a foundational platform on which most of the capabilities discussed in this report might imaginably be achieved in a 10- or 20-year time frame. This report discusses how the Digital Mathematics Library (DML) can make this network of information a reality.
WHAT GAPS WOULD THE DIGITAL MATHEMATICS LIBRARY FILL?
The real opportunity is in offering mathematicians new and more direct ways, through the Web, to discover and explore relationships between mathematical concepts (such as axioms, definitions, theorems, proofs, formulas, equations, numbers, sets, functions) and objects (such as groups, rings) and broader knowledge (such as the evolution of a field of study; and relationships between mathematical fields, concepts, and objects). Improved discovery and interaction in the proposed DML would make it possible to find and examine material on a much finer scale than what is currently possible, making connections easier to find, shortening the needed start-up time for new research areas, and formalizing some of the logic that mathematicians are already using in their research.
In Probability Theory: The Logic of Science, E.T. Jaynes discusses the reasoning that many mathematicians go through when approaching their work. He describes the strong form of reasoning as variations on the following: “If A is true, then B is true. A is true; therefore, B is true.” Weaker forms are assertions, such as “If A is true, then B is true. B is true; therefore, A becomes more plausible.” Jaynes states that
[George] Pólya showed that even a pure mathematician actually uses these weaker forms of reasoning most of the time. Of course, when he publishes a new theorem, he will try very hard to invent an argument which uses only the first kind; but the reasoning process which led him to the theorem in the first place almost always involves one of the weaker forms (based, for example, on following up conjectures suggested by analogies). The same idea is expressed in a remark of S. Banach (quoted by S. Ulam, 1957): “Good mathematicians see analogies between theorems; great mathematicians see analogies between analogies.” (Jaynes, 2003, p. 3)
The DML could help make these analogies easier to find and use.
Box 2.1 provides an example of how a mathematics researcher would start looking into a new topic, using Gröbner bases as a specific illustration. It shows some of the initial resources that are typically used and how their information varies from, complements, and supplements the other resources. It also shows how useful it would be to be able to pull much of this information into a unified source and make additional connections to other, lesser known resources and aspects of the literature.
The DML could aggregate and make available collections of ontologies, links, and other information created and maintained by human contributors and by curators and specialized machine agents with significant editorial input from the mathematical community. The DML could afford functionalities and services over the aggregated mathematical literature.
BOX 2.1
How a Mathematics Researcher May Currently Approach Information Gathering
Gröbner bases were first introduced by Bruno Buchberger for solving a range of problems in computational algebra and became an essential component of computer algebra software (Buchberger, 2006). Suppose a mathematician wanted to find out about this topic, perhaps because it was needed for a particular problem. First, when one types “Grobner basis” into MathSciNet, a list of around 2,400 chronologically ordered items appears, most of which are specialized papers. This is a potentially good resource for a specialist but is probably not ideal for the novice. If a similar search is done via Google Scholar, a list of research articles and books on the subject appear and are ordered by “popularity,” which usually reflects some version of page ranking. While some of the references provided by Google Scholar can be viewed, including some books on Google books, others are behind paywalls or are books that must be purchased before reading. In Google itself, the top five links are to Wikipedia,1 MathWorld,2 Scholarpedia,3 Mathematica code,4 and a survey article by Bernd Sturmfels.5
The Wikipedia article is limited and only contains four references but includes the book of Cox, Little, and O’Shea (1997), which is widely recognized and a premier introductory text on the topic. Wikipedia also offers suggested further reading and external links. Sturmfels’s article, from the “What is . . .” section of the Notices, is terse and contains only three references, but one of them is the aforementioned book. MathWorld’s article is short and lacks any specifics, but it contains a significantly longer list of references, survey articles, and several links to Amazon for buying books (and at least one dead link). The Scholarpedia article, written by Bruno Buchberger and Manuel Kauers, is more comprehensive and includes many illustrations, a wide range of applications, and a long list of references, including a Gröbner bases bibliography compiled by Buchberger and his coworkers at the Research Institute for Symbolic Computation.6 Unfortunately, no links are supplied in the Scholarpedia article to the other references. In many ways, Scholarpedia, which bills itself as a “peer-reviewed open-access encyclopedia,” could serve as one possible model for some aspects of the proposed DML.
All of these resources combined, along with the tenacity to pursue the variety of resources, can result in a good start in understanding Gröbner bases. However, suppose the researcher was working in an area that led to questions that Gröbner bases could be profitably used in, but, not being an algebraist, he/she did not know that they existed or even how to start to query any of the standard tools. Vice versa, suppose the researcher works in Gröbner basis theory and find results that could lead to advances in an area that he/she is not familiar with; how would the researcher know?
Here’s a real example: Although not well known, in fact, the theory of Gröbner bases was essentially discovered in 1910-1913 by an obscure Georgian mathematician, N.M. Gjunter, in his study of the integrability of overdetermined systems of partial differential equations (Renschuch et al., 1987). It is not immediately obvious through reference searching or the standard literature that Gröbner bases are
of importance in partial differential equations (although the Scholarpedia article does mention some applications to ordinary differential equations). Moreover, the latter area has resulted in the refined and potentially very useful concept of an involutive basis. This particular gap could be filled by editing the above mentioned articles, but this is simply one of innumerable similar cases. Making such unexpected links is not currently easy but could become so with a fully functioning DML, therefore increasing the serendipitous-like discovery of connections, which plays a role across research.
__________________________
1 “Gröbner Basis,” Wikipedia, http://en.wikipedia.org/wiki/Gr%C3%B6bner_basis, accessed January 16, 2014.
2 E.W. Weisstein, “Gröbner Basis,” MathWorld—A Wolfram Web Resource, http://mathworld.wolfram.com/GroebnerBasis.html.
3 B. Buchberger and M. Kauers, Groebner basis, Scholarpedia 5(10):7763, 2010.
4 “GroebnerBasis,” built-in Mathematica symbol, Wolfram Mathematica 9, last modified in Mathematica 6, http://reference.wolfram.com/mathematica/ref/GroebnerBasis.html.
5 B. Sturmfels, What is a Gröbner Basis? Notices of the AMS 52(10), 2005, http://math.berkeley.edu/~bernd/what-is.pdf.
6 B. Buchberger and A. Zapletal, Gröbner Bases Bibliography, http://www.ricam.oeaw.ac.at/Groebner-Bases-Bibliography/search.php.
While it would have to store modest amounts of new knowledge structures and indices, it would not have to generally replicate mathematical literature stored elsewhere.
The committee identified a number of basic desired library capabilities, including aggregation and documentation of information, annotation, search and discovery, navigation, and visualization and analytics. Properly implemented across the domain of mathematics research literature, these capabilities and resulting enhanced functionalities would not only facilitate better and more efficient search and discovery, but also allow mathematicians to interact with the research literature in new ways and at new levels of granularity. The proposed DML is much more than an indexing service and aims to create meaningful connections between topics by utilizing lists of entities and providing coherent access to a range of tools that can speed up mathematical discovery: for example, comprehensive encyclopedia articles and review articles, lists of mathematical objects, implication diagrams, and annotated bibliographies, informal annotations, and comments on articles. These tools and others are discussed in Chapter 5.
The DML would not only result in new efficiencies, thereby freeing up researcher time, but also enable experimentation with new approaches to
using and getting the maximum benefit out of the mathematics research literature. The remainder of this section describes each of these desired capabilities and illustrates how resultant improved functionality could advance mathematics research.
Aggregation and Documentation
Mathematicians want to be able to make searchable and sharable collections or lists of various kinds of mathematical objects easily, including bibliographies of the mathematical literature, perhaps with annotations. This is an area where it should be very easy to make rapid progress. The issues of mathematical object representations are mostly about who is allowed to create, view, and update various lists and about resource management. Many of these types of lists (such as those mentioned in Chapter 1) currently exist, some with connections to the literature, but their existence is often tied to the survival of the curator’s personal website. Providing a stable platform for housing and connecting these lists would also allow for this information to be incorporated in the collective knowledge of the DML.
The availability and interconnection between these lists would allow a larger network of mathematical information to be developed. This would be on a finer scale than what is currently available and facilitate higher-level features of advanced search and navigation. The world of mathematical knowledge goes much deeper than the level of research papers; it goes down into the content that is discussed within the papers, the knowledge that is assumed already to be understood by the reader, and the connections that exist between this information. If the DML could draw on this information, it would have a much more meaningful view of mathematics.
Lists of Mathematical Objects in New Areas
While many books contain fairly comprehensive descriptions of theorems relating to a specific subject and substantial stand-alone lists of theorems have been prepared, the committee is not aware of any truly comprehensive list of theorems in any branch of mathematics. Moreover, “lists” as embodied in books are not necessarily designed to enable all the functionality envisioned for the DML. There have also been several efforts to establish a formal computer-aided proof capability (Wiedijk, 2007), but it has not had much impact on the larger mathematics community. Mizar has published the largest such collection of about 50,000 formally checked theorems.1 New mathematical theorems and lemmas are proven and pub-
__________________________
1 Mizar Home Page, last modified January 8, 2014, http://mizar.org/.
lished on a routine basis.2 There have also been efforts to identify and list in order the most important mathematical theorems (such as the list presented by Paul and Jack Abad in 19993) based on assessments of their place in the literature, each theorem’s proof, and the unexpectedness of the result. Even if all existing theorems and lemmas were indexed and organized in some way, there needs to be a way to continually update this list with new work.
Although even a list of theorems would be valuable, or a collection of text articles about each theorem, modern knowledge representation techniques offer more ambitious possibilities. For example, collections of represented facts such as DBPedia4 or Freebase5 permit retrieval of data about the real world, such as populations or areas of nations and towns. Library and museum catalogs are being converted to formal Resource Description Framework (RDF)6 statements. Having a rigorous description of a theorem enables logical deduction and comparison of that theorem with others. The generality of mathematics is one of its beauties, and when the same form appears under two different names, it implies an unsuspected applicability of each theorem.
It appears within the grasp of modern information management tools to develop a machine-readable repository of mathematical theorems and definitions in which theorems are expressed as statements about terms, terms are linked to definitions, and definitions are constructed from logical statements about other terms. This is certainly very challenging, but the first steps in this direction have been made by Wolfram|Alpha for continued fractions, with a formalism for canonical representations of theorems that appears simple and flexible enough to be more widely adopted and used for purposes of search, retrieval, and linking. The Mizar Project also has a large database of formal theorem statements and formal proofs, although this is much less easily accessible to a working mathematician. How to do this on a large scale is still an open problem, but there are indications that efforts of this kind should be rewarding (Billey and Tenner, 2013).
Only the definitions and the theorem statements need to be machine-readable—the proofs can be LaTeX or a citation. Technologies like RDF
__________________________
2 In his 1998 biography of Paul Erdös, Paul Hoffman reports that mathematician Ronald Graham estimated that upwards of 250,000 theorems were being published each year at that time (Hoffman, 1987).
3 P. Abad and J. Abad, The Hundred Greatest Theorems, 1999, http://pirate.shu.edu/~kahlnath/Top100.html.
4 DBpedia, About, last modification September 17, 2013, http://dbpedia.org/About.
5 Freebase, http://www.freebase.com/, accessed January 16, 2014.
6 RDF is a standard model for data interchange on the Web and facilitates data merging even in the case of differing underlying schemas. See WC3 Semantic Web, “Resource Description Framework (RDF),” last modified March 22, 2013, http://www.w3.org/RDF/.
and OWL7 may be useful for encoding the theorems’ statements and the definitions. These technologies are flexible enough to allow users to extend the ontology, while encouraging reuse of existing terms. The markup languages used by automatic theorem provers could also be useful because they are sufficiently flexible to encode many important theorems, but they might not do enough to encourage reuse of terms.
The theorem and lemma repository would benefit from being accessible to programs via an application programming interface, which is a protocol used to allow software components to easily communicate with each other and may include specifications for routines, data structures, object classes, and/or variables.
Researchers will likely submit their theorems through a Web-based interface if it helps them to get citations and to stake a claim to having proved it first. There are a lot of famous cases where theorems were proven independently by multiple individuals using different terminology. A machine-readable repository could detect duplicate terms and theorems so that researchers can focus on new results rather than proving what is already known. The main benefit, however, may come from granting programs access to the latest mathematical results through user submissions.
Another data type worthy of consideration in a DML is problems. Good problems spur research advances. Problem lists have been created and maintained at various times, most famously Hilbert’s list of problems around the beginning of the 20th century. Some recent efforts at curation of problem lists are the Open Problem Garden8 and the the American Institute of Mathematics’ Problem Lists.9 A community feature encouraging creation and maintenance of problem lists with adequate links to the literature and indications of status could be an important component of the DML.
Annotation
Mathematicians want to be able to annotate mathematical documents in various ways and share these annotations with collaborators or students and, in some cases, publish these annotations for the benefit of a wider but closed group (a set of collaborators, or a seminar, or a cohort of doctoral students) or the general public. The ability to easily share notes could improve the learning curve for researchers in new areas, provide opportunities to learn from other researchers interested in similar topics, elucidate logic
__________________________
7 W3C, “OWL Web Ontology Language Overview,” February 10, 2004, http://www.w3.org/TR/owl-features/.
8 Open Problem Garden, http://www.openproblemgarden.org/, accessed January 16, 2014.
9 American Institute of Mathematics, AIM Problem Lists, http://aimpl.org/, accessed January 16, 2014.
that is not explicitly stated in papers, allow authors to post corrections, and overall enrich the research discussion. Some mathematicians prefer to keep comments limited to a smaller group, while others are more comfortable posting openly. Either way, this enhancement to the traditional research paper could quicken the path toward understanding and at the same time enhance the DML’s capability to traverse the literature.
The ability to see others’ annotations as well as create new annotations would make reading a paper not only easier, but potentially more interesting. Some links could point to other items residing in the digital library, while others point to popular sites such as MathOverflow and Wikipedia or other sites outside the DML. For researchers setting out in a new direction or for researchers in an isolated location, it is often difficult to get involved in a lively conversation with fellow researchers. Links to discussions and comments on research papers and theorems could be a way to expand research discussions to a new level. Senior mathematicians could provide some general background information to research papers, such as a basic prerequisite for understanding the paper and some suggested readings; this would assist students and people starting out in a new direction. It should be possible for individual users to tailor the writing and reading of comments. It could also be useful to be able to select or prioritize, in several possible ways to be set by each user individually, the comments that appear on one’s screen while searching (e.g., so as to see most prominently the comments from other members in an existing collaboration group or from a commenter one has experienced earlier as particularly insightful on a particular topic).
An important component of successfully providing an annotation feature within the DML is separating unhelpful comments and deciding which annotations will be kept in the system. Nearly every system that allows public comments also has a way to flag unconstructive comments and responses as inappropriate for that platform. A system such as this may need to be developed for the DML and refined based on the kinds of comments and feedback that the DML receives. One example of this is how MathOverflow deals with user input that its established users deem to be spam, offensive, or in need of attention for any other reason.10 Elected community monitors are established within MathOverflow, and experienced users are able to flag comments and posts for a moderator’s attention. The moderator can then decide what action is needed (deleting spam, closing off-topic posts, removing poorly rated posts, and so on). A system like this may work well for the DML.
__________________________
10 MathOverflow, Help Center, Reputation and Moderation, “Who are the site moderators, and what is their role here?,” http://mathoverflow.net/help/site-moderators, accessed January 16, 2014.
General support for the creation of basic text annotations has been available for some time, including for mathematics literature made available as PDF or in HTML format. Support for more sophisticated forms of semantic annotation and for the sharing of annotations across disparate content repositories is rapidly maturing through technology from other domains,11 but these technologies have yet to be customized for use in mathematics. Adapting these technologies to the mathematical community requires adequate support for mathematical markup. Some Web services are expanding into mathematical markup. For example, Authorea12 uses a robust source control system in the backend (git) and an engine to understand LaTeX, Markdown, and most Web formats. Authorea lets users write articles collaboratively online, and it renders them in HTML5 inside a Web browser. Authorea is a spin-off initiative of Harvard University and the Harvard-Smithsonian Center for Astrophysics.
There are numerous other tools available that provide for “wiki-like” structured discussions with attribution dates and hierarchical organization, such as PBWorks.13 There are also tools for highlighting, summarizing, providing video and audio annotation, mapping documents, and collaborative reading; some are specialized to particular document formats, and some are not. The Mellon project on Digital Research Tools14 has a list of more than 500 tools, of which nearly 80 are tagged as annotation systems. Some are automated (e.g., part of speech tagging), but most are tools for use by readers or writers, either individually or in groups.
Adding this capability to the readily available digital literature should not be overly complicated. There would need to be conventions established for where the annotations are stored and who is responsible for storing them, and the best default setting for privacy and sharing would also need to be established. These annotations can provide a bridge to community-sourced markup of objects or a way to pass information to editors (human-or software-based) that curate the collection, thereby further enriching the DML. This is just one way in which user and community input would play a role in the DML; many others are listed elsewhere in this report. Community support for the new digital library will be essential for its success and
__________________________
11 World Wide Web Consortium (W3C) Open Annotation Community Group (http://www.w3.org/community/openannotation/), Domeo (life science domain, http://swan.mindinformatics.org/), Shared Canvas (humanities domain, http://www.shared-canvas.org/), Maphub (annotation of maps, http://maphub.github.io/), Pundit (annotation of Web content, http://www.thepund.it/), and LoreStore/Aus-e-Lit (collaborative annotation of literary works, http://www.itee.uq.edu.au/eresearch/projects/aus-e-lit), all accessed January 16, 2014.
12 Authorea, https://www.authorea.com/, accessed January 16, 2014.
13 PBWorks, http://pbworks.com/, accessed January 16, 2014.
14 Andrew W. Mellon Foundation, Bamboo DiRT, http://dirt.projectbamboo.org, accessed January 16, 2014.
also an essential way in which it could be much more than just a collection of mathematical information and links to other repositories and services.
Recommendation: A primary role of the Digital Mathematics Library should be to provide a platform that engages the mathematical community in enriching the library’s knowledge base and identifies connections in the data.
Search and Discovery
Mathematicians want to be able to understand mathematical objects—such as an equation, theorem, or hypothesis—more effectively and with greater ease. This quest can be aided by having the ability to specify a mathematical object either in natural language or more formal notation and get information on where other uses of the object appeared in the literature, definitions of the object, or related objects of interest. For example, consider questions of the form: “Given a hypothesis, what theorems involve this hypothesis?” or “Given a partial list of hypotheses and some conclusion, what additional hypotheses are known to imply the conclusion?”
The ability to ask and receive meaningful information about questions such as these is largely out of reach of current technology. It will require considerable research and investment to get even partway there. But the committee sees first steps toward realizing such capabilities in the innovative work of Wolfram|Alpha in the restricted domain of continued fractions. 15 Wolfram|Alpha prototyped and built a technological infrastructure for collecting, tagging, storing, and searching mathematical knowledge of continued fractions and presents it through a Wolfram|Alpha-like natural language interface. The main types of knowledge provided in this work are theorems, mathematical identities, definitions and concepts, algorithms, visualizations and interactive demonstrations, and references.
The committee believes there are many other subdomains within mathematics where significant advances on such very difficult problems may be possible with some mixture of modern methods of natural language processing and machine learning, expert human analysis of the literature of the subdomain (aided by computer), and knowledge representation approaches. Beyond hints of broad feasibility, the WolframlAlpha experience suggests the following:
__________________________
15 M. Trott and E.W. Weisstein, “Computational Knowledge of Continued Fractions,” WolframAlpha Blog, May 16, 2013, http://blog.wolframalpha.com/2013/05/16/computational-knowledge-of-continued-fractions/.
- Key characteristics may be identified to make specific subdomains more feasible;
- It is possible to understand which of those subdomains are likely to be valuable to mathematicians, if they are appropriately captured and represented; and
- It is possible to understand how to encode knowledge so it is not specific to a single computing platform.
From here, one could imagine funded investments to encode specific mathematical subdomains in parallel to investment in work on the more general problem. Such subdomain-specific campaigns could be carried out as part of larger literature analysis efforts in the subdomain, which would build up or enrich the ontology and the link databases of the DML.
Intelligent information extraction and transfer are needed. For instance, it would be helpful if a user could just highlight a formula and then click on a button that submits the formula to a DML service that responds to some obvious questions, such as the following:
- Is this a well-known formula?
- Is it close to one in some curated list of formulas?
- Does it have a name? A homepage?
- Can it be parsed directly into a rigorous format for computation? If not, can the user be provided with some indications of the ambiguities encountered in parsing, and make choices as to which meaning is intended?
Moreover, it would be useful to be able to do this for more complex objects such as theorems and hypotheses. The committee does not wish to be too prescriptive about exactly how such capabilities and services might develop. In some specific domains, such as special functions and integer sequences, the necessary database of mathematical information is largely already constructed. The remaining issues are as follows:
- Social—Getting data to where they can be machine processed for development of services, and
- Technical—Building an adequate human-computer interface to enable users to interact with such databases in their everyday mathematical work.
The committee sees enormous potential for developments in this area by some concerted research effort involving a team of people with complementary expertise in machine learning, natural language processing, human-computer interaction, and mathematical knowledge representation. The
key is to attract some sustained interest of people with relevant expertise in working together to produce DML capabilities of this kind.
Searching for/in Mathematical Equations or Formulas
Mathematical papers are rife with complex equations and formulas; a few examples (from different mathematical subfields) are given in Figures 2-1, 2-2, and 2-3. It is clear that these expressions are a daunting
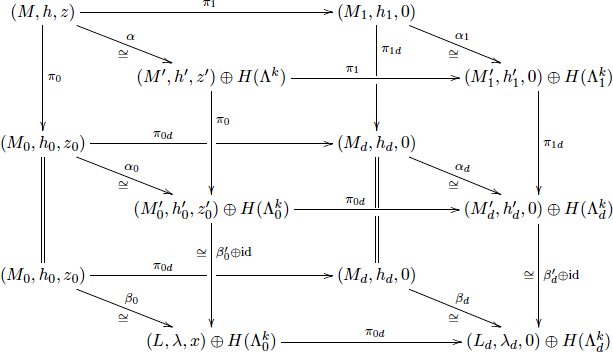
FIGURE 2-1 An example of complex mathematical typography. SOURCE: Lee and Wilczyński (1997).
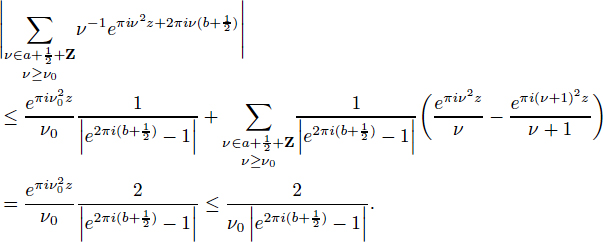
FIGURE 2-2 An example of complex mathematical typography. SOURCE: Zwegers (2008).
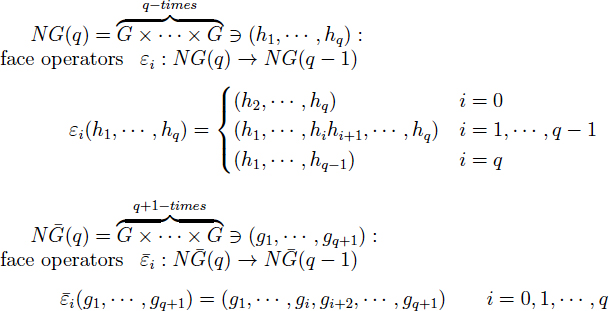
FIGURE 2-3 An example of complex mathematical typography. SOURCE: Suzuki (2013).
challenge to search or classify because of their complex notation, reliance on formatting not standard in other disciplines, and extreme precision. Even searching for notationally simpler concepts such as the historical evolution of an equation, whose name and notation may have been evolving for decades, is challenging. However, there exist several approaches that, separately or in combination, could be useful for this purpose. Many recognition tools are not based on a conceptual understanding of what one seeks to recognize, but rather on statistical analysis of usage patterns.
For instance, Google has a very good spellchecker (“Did you mean X?”) that is based not on a deep conceptual understanding of the transformations possible on English words (i.e., morphology), but on statistical modeling of what humans typically type in as queries. For example, if one asks Google to search for “wavelette,” it suggests “wavelet” as a more appropriate target, because lots of people have typed “wavelet” into the system in the past and only a few have typed “wavelette.” To do this, the system needs to figure out that these two things should be connected, which is feasible given co-occurrences with other words in previous queries.
Another recognition example is Duolingo,16 which uses a crowd-sourced model to translate content and vote on translations. Users of Duolingo sign up to learn and perfect their use of a foreign language; in the process, their feedback assists a project that produces high-quality translations of webpages. Originally, the Duolingo team expected to use insights
__________________________
16 DuoLingo, http://www.duolingo.com/, accessed January 16, 2014.
from experts on how people learn languages. However, it is far easier and as effective to collect statistics on usage and let those guide the make-up of the successively more sophisticated tasks given to the users learning a language (von Ahn, 2011).
Because mathematical expressions are more complex than the word spellings handled by the Google spellchecker, the first step in characterizing them for clarification would be to bring them into, or describe them in, some form amenable to such statistical analysis. There exist several possible directions that could be followed, of which some are discussed below.
One approach would be to use feature vectors such as the Scale-Invariant Feature Transform (SIFT) to characterize mathematical expressions. Computer vision experts introduced SIFT for images, which can be used to “recognize” images or objects represented in images, independent of some warping, scale changes, or variations in illumination, by comparing feature vectors that keep track mainly of the statistics of many different types of local features, without trying to build a higher-level vision model of the objects depicted in the images (Lowe, 2004; Bosch et al., 2007). One may wonder whether it might be possible to likewise characterize some complicated mathematical expressions by a list of features that would then be useful in recognizing (variations of) it in other papers. Although SIFT features themselves are designed for image analysis, the general idea of attaching features to objects and then classifying them is extremely powerful. Objects can currently be retrieved or clustered based on words, tags, or descriptions in general (author, date, and so on). If properties of equations and theorems could be identified that were characteristic of their meaning, discriminating between different equations, and easy to detect, then techniques from information organization could be applied to help with browsing and searching.
A different approach would be to describe the way the formula is constructed geometrically, similar to the International Chemical Identifier (InChI)17 for chemical substances. InChIs, which are nonproprietary identifiers for chemical substances that can be used in printed and electronic data sources, are specifically designed to enable easier linking and searching of diverse data compilations. InChIs can be computed from structural information and are human readable (with practice). Graphical representations of chemical substances are automatically converted into unique InChI labels, which can be created independently of any organization, built into any chemical structure drawing program, and created from any existing collection of chemical structures (Heller et al., 2013). It is conceivable that a similar automatic characterization could be done for mathematical formulas,
__________________________
17 International Union of Pure and Applied Chemistry, “The IUPAC International Chemical Identifier (InChI),” http://www.iupac.org/home/publications/e-resources/inchi.html, accessed January 16, 2014.
which are two-dimensional graphical representations of the mathematical concepts they describe. If it were possible to determine international mathematical formula identifier labels, these could be extremely useful for searching and linking mathematical papers.
Yet another approach would be to create an ontology to characterize mathematical expression, similar to what Linnaeus created for biology. Linnaeus’s Systema Naturae (Linnaeus, 1758) advocated the systematic and consistent use of a uniform botanical and zoological nomenclature in which each species is characterized by a two-word description: the first is the genus (which could, in principle, be decided for each specimen by examining just a few of its characteristics, even by people with limited expertise), and the second name specifies the exact species within the genus. In particular, Linnaeus’s classification of plants was based on only their reproductive organs. By counting pistils and stamens of a plant, anyone, even without much botanical knowledge, could get a listing of genera that the plant in question should belong to. Prior to this system, botanical nomenclature was completely disorganized, and a botanist would describe a specimen by composing a long multiple-word descriptive name providing what seemed to be the list of most relevant and distinguishing characteristics, leading to different descriptive names for specimens of the same species. The two-tier system promulgated by Linnaeus provided a “tag” of which the first term (the name of the genus) could be relatively easily determined, followed by a search for the exact, lengthy description within that genus for a specific species, which made it possible to determine that the specimen was a new species. This system was first heavily opposed, but was gradually adopted by botanists.
While this system is currently under revision due to the widespread availability of genomic information, it is still a useful example of how ontologies can play an important role in establishing structures that promote the ease of comparing and searching. As compared to some scholarly domains, mathematics is fortunate to have a significant de facto standard ontology around which its research literature is organized. The Mathematical Subject Classification (MSC) standard ontology is used by both MathSciNet and zbMATH, meaning that more than 3 million research articles, chapters, and proceedings papers are already indexed using this scheme.
However, MSC is designed for indexing resources at the granularity of articles or conference proceeding papers. It exposes article topics in a broad way, but does not expose, for example, the theorems, functions, or sequences proven, used, or discussed in a paper. To support a broad range of discovery, browsing, and use cases, mathematicians need access at finer granularities, and they need descriptions created from viewpoints that go beyond the traditional library bibliographic cataloging perspective. In short, new ontologies will be required.
There is a foundation on which to base some of these supplemental ontologies. MathSciNet and zbMATH provide strong personal and journal name authority control back to the middle of the 20th century. The MathSciNet authors’ database indexes more than 660,000 distinct authors. This database can be searched by name and/or affiliation with excellent recall and precision. In the context of linked data and the Semantic Web, this database also can be used (and has been used by MathSciNet) to generate such things as collaboration graphs, which are useful (for example) for calculating a “collaboration distance” between any two authors. This in turn provides another way to fine tune browsing and searching (e.g., searching for works by an individual or any other author within a certain collaboration distance of the original individual) under the assumption that such authors might have ideas that are related in some fresh way to the smaller collection of articles directly cited.
Other ontologies could be developed from resources that organize objects and concepts found within the mathematical literature. A particularly rich and promising example is the On-Line Encyclopedia of Integer Sequences (OEIS) (see Appendix C), which names and indexes more than 200,000 sequences. OEIS is particularly attractive for use as the foundation of an ontology for organizing the literature at a finer granularity, because it uses persistent identifiers for sequence entries and because most entries already include at least some bibliographic references.
Most retrieval from text is based on the words in the text; by contrast, many of the actual symbols in a mathematical equation are not useful search terms (e.g., a search for the indices i, j, and n would not be useful). And strings of symbols are only partially useful as search terms; for example, the following three equations
![]()
are all mathematically equivalent definitions of a quadratic function and should be considered so, even though the symbols have changed and elementary mathematical manipulations intervene. Similarly, the context of the variable x, t, or s may itself change, indicating a real or complex number, or a quaternion, or perhaps a matrix or linear operator, although within a given work, the notation is usually gradually fixed so that, say, x always represents a real variable. There are, however, certain conventions such as p being often reserved for the irrational number and matrices usually being denoted by capital letters. Tensor analysis, in particular, utilizes strict conventions on the meanings and arrangement of subscripts and superscripts, as well as often employing the Einstein convention of implied summation on repeated indices.
As noted above, identifying the subfield of a mathematical paper may help disambiguate the notation. For instance, the (not uncommon) nota-
tion π for a generic permutation of a finite number of items is less likely to be confused with 3.141592… when the context is already identified as pertaining to combinatorics rather than analysis or geometry. In practice, it may well be that once sufficient statistics on usage have been collected, such disambiguation could be done based on only statistical data.
Additional problems are posed by the historical literature: as a field evolves, notations and terminology change, making connections to older literature treating the same mathematical objects even more daunting. Historically, notation conventions may vary where change is a reflection of increased complexity and deeper understanding. In mathematics literature, the gradual evolution in terminology and notation includes disputes that usually (but not always) get resolved on what to call and how to represent concepts, theorems, objects, etc. The evolution also reflects the integration of work spanning many languages and cultures, each with their own idiosyncrasies. Mapping back to earlier representations and concepts may not be straightforward or direct.
In order to provide the careful typesetting modern mathematicians require, precise typesetting and document preparation systems have been developed, of which the most widely used is TeX,18 together with its descendants LaTeX, LaTeXe, etc.19 TeX and its derived systems lead to nicely typeset formulas (all the examples in Figures 3-1, 3-2, and 3-3 were realized this way), and they have become an indispensable tool for mathematicians (most of whom do their own typesetting for papers they submit for publication). At first sight, the LaTeX source code for a formula could be thought a good candidate for an international mathematical formula identifier. However, LaTeX is a presentation format, and equations in LaTeX cannot be easily converted to a semantic representation that can be used in other contexts. As a simple example of this problem, finding a string in italics might mean, depending on the context and style, that it is a journal title or a foreign word; to present the document in a different format or create metadata, one needs to know the semantic significance underlying the typographic display. Often, there is no one-to-one correspondence between a mathematical formula as it appears on the printed page and the LaTeX instructions leading to it; this nonuniqueness is even more pronounced if one takes into account small variations in spacing (or changes of names of variables, as illustrated above) that would not affect the reading of the mathematical meaning of the formula by a mathematician. In this sense, the LaTeX code for a formula would seem to fall short as a direct template for a putative international mathematical formula identifier (as discussed
__________________________
18 “TeX,” Wikipedia, last modified January 7, 2014, http://en.wikipedia.org/wiki/TeX.
19 LaTeX—A document preparation system, last revised January 10, 2010, http://www.latex-project.org/.
earlier in this section). However, the National Institute for Standards and Technology Digital Library of Mathematical Functions20 uses metadata embedded in the LaTeX code used to typeset the formulas to enable formula and notation search. This LaTeX metadata search, while not quite a LaTeX formula search, is fairly successful in dealing with dynamic notation and terminology change in the literature of special functions.
An option for semantic representation of mathematical formulas can be provided by MathML,21 which allows for mathematics to be described for machine-to-machine communication and is formatted so that it can easily be displayed in webpages. There have already been some research efforts along the lines suggested above, and there are a limited number of both experimental and production systems available that involve some kind of formula search. In particular,
- There is some level of formula search in EuDML, using MIaS/ WebMIaS (Math Indexer and Searcher),22 a math-aware, full-text-based search engine developed by Petr Sojka and his group (Sojka and Líška, 2011).23 An approach based on Presentation MathML using similarity of math subformulae is suggested and verified by implementing it as a math-aware search engine based on the state-of-the-art system Apache Lucene.24
- Some type of characterization of formulas is inherent to the searches underlying the Wolfram|Alpha engine. As part of a project in seeing whether mathematicians would find it useful to be able to search the literature for formulas, Michael Trott and Eric Weinstein of Wolfram|Alpha implemented some characterization of formulas for the research literature on continued fractions (essentially programming it “manually”). This small, fairly contained body of literature was chosen because most of the relevant papers are now in the public domain. However, the field of continued fractions is not very active at this point, and it may be hard to get a good sample basis of users to assess whether this search capability would lead mathematicians to new ways of using or searching the
__________________________
20 National Institute for Standards and Technology (NIST), Digital Library of Mathematical Functions, Version 1.0.6, release date May 6, 2013, http://dlmf.nist.gov/.
21 W3C, “Math Home,” updated November 26, 2013, http://www.w3.org/Math/, accessed January 16, 2014.
22 EuDML@MU, “MIaS/WebMIaS,” last change October 28, 2013, https://mir.fi.muni.cz/mias/.
23 See also Petr Sojka’s webpage at Masaryk University, Brno, last updated December 3, 2013, http://www.fi.muni.cz/usr/sojka/.
24 Apache Software Foundation, “Apache Lucene Core,” http://lucene.apache.org/core/, accessed January 16, 2014.
literature. It should be noted that the Mathematica-based formula characterization/search underlying Wolfram|Alpha is proprietary, in contrast to the completely nonproprietary nature of the InChI, which would also be desirable for an international mathematical formula identifier.
- Springer LaTeX Search25 allows researchers to search for LaTeX-formatted equations in all of Springer’s journals. In an issue of “Author Zone,”26 Springer’s eNewsletter for authors, Springer reveals that this free tool, which searches over a corpus of 120,000 Springer articles in mathematics and related fields, was created by 8 months of engineering a process that normalizes LaTeX equations. An open tool such as this would be valuable to the DML and to other mathematical indexing services.
Finding: While fully automated recognition of mathematical concepts and ideas (e.g., theorems, proofs, sequences, groups) is not yet possible, significant benefit can be realized by utilizing existing scalable methods and algorithms to assist human agents in identifying important mathematical concepts contained in the research literature—even while fully automated recognition remains something to aspire to.
Navigation
Mathematicians want the ability to navigate and explore the corpus of mathematical documents available to them, be it through institutional library services or through free services. This goes well beyond accessing electronic versions of papers by following citations. The ability to click on an object in a document and be able to quickly find additional information about that object might help a mathematician decide whether to examine it further. Such additional information on an object might include the following:
- Other articles discussing the same object, or perhaps slightly more general or specific objects (and not necessarily with the same names);
- A description of when and where that object was first defined in the literature;
- A list of reference resources (textbooks, encyclopedia entries, survey articles) with information about the object; and
__________________________
25 Springer, LaTeX Search, http://www.latexsearch.com/, accessed January 16, 2014.
26 Springer, “LaTeXSearch.com: Introducing the latest Springer eProduct in the field of Mathematics,” http://www.springer.com/authors/author+zone?SGWID=0-168002-12-693906-0, accessed January 16, 2014.
- Different representations of the object (such as a LaTeX fragment or as Mathematica®code).
This is an area where it should be possible to make rapid progress, given a foundational DML investment in ontologies and links.
Improved navigation of the mathematics literature would enhance research capabilities in several ways. It would allow a researcher to find different resources and publications more easily and to find seemingly unrelated but relevant topics within the literature. It would also help a researcher to address the simply stated but inherently complex question, “Has this been done before?” Being able to answer this question would save valuable research time and simplify the problem-solving track, all while making the existing literature’s structure more transparent and easy to use.
The Citation Graph
Research articles can be viewed as the vertices in a large directed graph in which article A “points to” article B if A cites B. This citation graph is mostly tree-like: references are typically to older articles, although there are certainly cases of more or less contemporaneous articles that cite each other; some larger loops probably exist as well. Researchers interested in learning about a new direction or subject typically explore this graph; they start reading a particular research paper of interest and then climb back along the branches, reading some of its references and then some of the references of those papers, and so on. The creation of a citation index, as provided by MathSciNet within mathematics and by Google Scholar, Scopus,27 and Web of Science across many more fields, allows the user to traverse the graph in the reverse direction, that is, to find for each paper all the articles that cite it. This very useful search tool makes it possible to easily find recent developments based on a paper of interest. Users would then be able to easily integrate or compare such information with whatever could be provided by other indexing services.
Making such comparisons or aggregations is at present very difficult. An expert user can do it in a few clicks by cutting and pasting from one browser window to another, but it is a few clicks for each resource, perhaps 12 clicks to compare returns from all three of these services. But with modern browser extension capabilities, such as those provided by Scholarometer,28 which harvests data from Google Scholar, it is straightforward to write a dedicated browser extension for mathematical search
__________________________
27 Elsevier B.V., Scopus, http://www.scopus.com/home.url, accessed January 16, 2014.
28 Indiana University, Scholarometer, http://scholarometer.indiana.edu/, accessed January 16, 2014.
and retrieval that would take a reference string from almost any source. The committee sees this kind of on-the-fly querying and aggregation of data from multiple services as the solution to the vexing compartmentalization problem for indexing services.
A DML navigating tool could incorporate some mechanism for sorting and prioritizing the references it produces. A desirable feature of an open service is that such algorithms for ranking could be adjusted if so desired by the user, based on some special search criterion tailored by the searcher right then, or possibly influenced by the searcher’s past preference behavior that is recorded by the system. Other basic questions that can be addressed by integration of DML data with data from various more-or-less-cooperative search service providers include the following:
- Which articles are cited in this paper? (This information is typically provided in the paper’s list of references.)
- Which articles cite this paper? (This is a search that looks forwards in time, looking for papers that list this paper as a reference.)
- Which articles cite both papers A and B?
- Which articles are cited in both A and B?
Techniques for data analysis using methods such as bibliographic coupling and citation analysis are well established, and available software could be deployed for the benefit of DML users. A significant amount of citation data in mathematics and related fields is already more or less openly available from various open-access sources.
It should be possible to assemble accessible enhanced visualizations and graphical displays that capture features of a bibliographic data set that are not easy to find in a textual representation, and to make these features useful for search. Interactions between objects in a data set can be revealed by graphical displays within a browser (MacGillivray, 2013). Search results can be visualized in open formats, such as Scalable Vector Graphics (SVG),29 and can be obtained from open search systems such as Lucene30 or ElasticSearch.31 Because today’s widespread availability of all kinds of data is increasing attention on the need for better visualization tools, the committee anticipates that greatly improved open-source tools for graphical displays will become widely available and easily deployable to demonstrate interesting and novel features of the graphical relations in bibliographic
__________________________
29 “Scalable Vector Graphics,” Wikipedia, http://en.wikipedia.org/wiki/Scalable_Vector_Graphics, accessed January 16, 2014.
30 Apache Software Foundation, “Welcome to Apache Lucene,” http://lucene.apache.org/, accessed January 16, 2014.
31 Elasticsearch, http://www.elasticsearch.org/, accessed January 16, 2014.
data sets, not just those derived from citation graphs, but also those from collaboration graphs32 and other graphs associated with relations between mathematical entities, such as implications or similarities.
As more data about the citation and collaboration graphs in various disciplines have become available, they have also been used as a tool for ranking the impact of specific scholarly journals over time and have begun to be factored into the evaluation of individual researchers within the tenure and promotion process, where enthusiasm about their quantitative and “objective” nature has increasingly overcome very real concerns about their limitations and inaccuracies as a measure of the impact of a given scholar. A good deal of work has been done proposing various so-called alternative metrics (“alt-metrics”)33 for scholarly impact both at the article level and aggregated to characterize the contributions of a scholar (e.g., the h-index34). Analytics of these sorts are more likely to be useful to track topics than to measure the worth of theorems, journals, or individuals because often they are easy to manipulate and do not accurately reflect the community’s view of importance (Arnold and Fowler, 2011; López-Cózar et al., 2013).
There is also real interest among working scholars in the possibility of tracking the evolution of these graphs (probably in conjunction with other data, such as popularity of articles) in order to help allocate precious reading time by identifying emergent, potentially high-impact or high-interest articles within or across specific subdisciplines, and a hope that article-based metrics can be developed to assist with this. The availability of citation and collaboration graph data, in combination with other information provided by the DML, would be an important step in advancing these research programs.
Tracking Article-to-Article Reading
Beyond simply exploring the citation graph, it may be desirable to obtain and exploit information about what other users of the DML have found useful as they explored the graph. For instance, what is the answer to the question, “Which articles did readers like, who are (like me) interested in A1, A2, and A3?” This way, one could find papers that do not specifically reference each other but concern the same topic. (This type of linking
__________________________
32 Collaboration graphs are already attractively viewable on Microsoft Academic Search with the proprietary Microsoft Silverlight software.
33 Altmetrics, “Altmetrics: A Manifesto,” v 1.01, September 28, 2011, http://altmetrics.org/manifesto/.
34 The h-index is an index that attempts to measure both the productivity and impact of the published work of a researcher based on the set of his/her most cited papers and the number of citations that they have received in other publications (Hirsch, 2005).
is a routine task, practiced by many online stores: “others who liked this also liked. . . .”) It does, however, rely on a large user base to traverse the various graphs involved. Such a user base could be developed only with strong incentives for users to participate, such as superior navigation and search tools, so it is to be expected that such methods will be useful only late in DML development.
Recommender systems, like the one described in the previous paragraph, based on user tracking or ones based on “liking” a paper or topic within a system, are not new and are currently employed by Google Scholar and Elsevier, among others. They could also be developed within other information resources such as arXiv and MathSciNet.
These methods also raise privacy issues as users navigate a network of DML information. Concerns about privacy issues can often be addressed with customizable privacy settings (e.g., private navigation without login, public navigation with some anonymization of users, and possibly public navigation with public identity). It is important that the different models for maintaining user privacy are examined and assessed, and that a meaningful approach toward privacy be established for the DML.
Widely available machine learning algorithms can be used to predict the preference rating of as-yet-unseen articles by a customer for whom only a very partial profile is available, based on (often equally partial) profiles of other customers. A highly publicized recent success was achieved through the Netflix Prize competition in which Netflix “sought to substantially improve the accuracy of predictions about how much someone is going to enjoy a movie based on their movie preferences.”35 The final winning algorithm in that contest was an intelligent combination of strategies that alone produced insufficient improvement. This demonstrated that substantial progress can be achieved by combining different approaches that may be less spectacular when evaluated independently of one another. Such incremental improvements may not be very interesting from the perspective of machine learning research, but they are potentially useful in production applications of machine learning algorithms that the DML could provide.
The Mathematical Concept Graph
Mathematical research can also be aided by considering mathematical objects other than papers, through exploration of their connections in a directed graph. For instance, in the answer to the question, Which theorems or papers use theorem T?, the different links would likely be references to classical results and to later improvements that were made since theorem T first appeared. The committee imagines both supervised and unsuper-
__________________________
35Netflix, “Netflix Prize,” http://www.netflixprize.com/, accessed January 16, 2014.
vised learning approaches to these problems. In supervised learning, the machine starts from a list of known concepts, say functions or theorems, and then attempts to identify various instantiations of that concept. This is similar to automated library cataloging with a fixed structure of categories. Unsupervised learning is instead a process of clustering of instances—for example, deciding which theorems are essentially the same. At the level of LaTeX encoded formulas, some version of this capability, and a consequent search-and-discovery mechanism, is already achieved by Springer’s LaTeX Search capability.
As further motivation for such efforts, which may be very challenging, the committee notes that Don Swanson identified useful public, yet undiscovered, knowledge in the biomedical domain by examining under-explored connections between clinical observations (Swanson, 1986, 1987). Despite efforts over the past few decades to automate the discovery of new scientific hypotheses based on literature analysis, insight from a human researcher is still needed. Ganiz et al. (2005) suggested that domains other than medicine should be explored. The committee believes that similar “literature discovery” methods could lead to interesting (and underexploited) connections between different mathematical fields or results.
Visualization and Analytics
One way to help mathematicians learn from the large, complex, and rapidly growing and evolving literature base is to employ tools that are being developed to analyze data in a wide variety of settings, including both visualization tools and other analytical and statistical approaches. These tools could exploit the natural graphical structure of co-authorship and citation graphs and the relations among various kinds of mathematical objects and the parts of the literature that discuss these objects (as described in the previous section). The availability of an ontology for mathematical objects is important, and new tools are being developed that perform visualization guided by both an ontology and a set of data tagged according to the ontology (such as a collection of papers, or theorems, in a mathematical scenario). Note that in most cases, the committee expects that general-purpose graph analysis and visualization tools will be used, not tools developed by the DML.
The DML’s role would be to help mathematicians find the right tools and ensure that data from the mathematical literature and knowledge base are available in forms and formats, and through interfaces, that make it easy to use these general purpose tools. Presumably, progress in this area would be quick, given the availability of the DML’s underlying ontology and link collections, because it can build on other large investments that are under way already.
The committee does not expect the DML to be a contributor, but rather a testbed, for deploying methods for visualizing data. There are many widely deployed methods that can be applied to bibliographic data on the scale envisioned for the DML, which is modest compared to many big data projects. Microsoft Academic Search36 already provides attractive displays of the collaboration graphs across its corpus using its proprietary Silverlight™ software. While open-source alternatives would be more attractive, either the DML or other agents could easily offer such displays over DML data as soon as they are collected. This would provide an advantage over the quality of text data displays offered by the mathematical reviewing services. Similar displays could easily be provided for navigation and indication of relations between subjects at the level of MSC2010, which would greatly improve on past efforts.
Computational Capabilities
The committee wishes to promote cooperation between the DML and computational service providers to allow users functionality, such as being able to cut a formula out of a mathematical document and paste it into a computing environment. This can already be done to some extent for simple formulas by cutting, massaging, and pasting a formula into Wolfram|Alpha, which uses natural language processing methods to match natural language queries with more formal knowledge representations.
The mathematics community uses a variety of simulation software—both numerical (such as Matlab,37 Octave,38 Python,39 R,40 Origin41) and symbolic (such as Maple,42 Mathematica,43 Sage44). Most software tools have different formatting requirements, and these would have to be taken into account when transporting formulas to and from them.
_______________________
36 Microsoft Academic Search, http://academic.research.microsoft.com/, accessed January 16, 2014.
37 MathWorks, MATLAB, “Overview,” http://www.mathworks.com/products/matlab/, accessed January 16, 2014.
38 GNU Octave, http://www.gnu.org/software/octave/, accessed January 16, 2014.
39 Python Software Foundation, “Python Programming Language—Official Website,” http://www.python.org/, accessed January 16, 2014.
40 R Project for Statistical Computing, http://www.r-project.org/, accessed January 16, 2014.
41 OriginLab Corporation, “Origin,” http://www.originlab.com/index.aspx?go=Products/Origin, accessed January 16, 2014.
42 Maplesoft, “Maple 17,” http://www.maplesoft.com/products/maple/,accessed January 16, 2014.
43 Wolfram, Mathematica, http://www.wolfram.com/mathematica/, accessed January 16, 2014.
44 Sagemath, homepage, http://www.sagemath.org/, accessed January 16, 2014.
Recommendation: The Digital Mathematics Library should rely on citation indexing, community sourcing, and a combination of other computationally based methods for linking among articles, concepts, authors, and so on.
Other Useful Features
Application programming interfaces, which allow for add-on applications to be built by independent users and groups, are useful for experimentation with the processing of and understanding of mathematics. There are likely other tools that the DML could support that would be useful to the mathematics community.
For instance, there is still a need for a good pdf reader for mathematics. Most mathematicians still print out papers they really want to read, even if they own and mostly use an e-book reader for their other reading needs. When asked why they prefer reading mathematics from a print-out, researchers told the committee that they want to be able to flip back and forth, have difficulty concentrating on an electronic version, and miss the ability to annotate the paper with a pen or pencil. The DML could provide an environment to try out experimental readers.
Even prior to the existence of the DML, one could gain experience and better understanding of the feasibility and value of these technologies with the help of testbed platforms. These could serve as a framework for research programs to explore promising technologies and services, including extraction and identification of mathematical objects and applications of tagging or classification (including, perhaps, community-sourced approaches).
Experiments with structuring math knowledge into Wolfram|Alpha have been very promising and provocative. These are worth extending into other areas to gain additional understanding of effectiveness and limits. It would be of interest to select areas that are of active research interest. A key issue here, however, is understanding how to extend or share this beyond just Wolfram|Alpha and to make the investment reuseable in other settings.
Arnold, D.N., and K.K. Fowler. 2011. Nefarious numbers. Notices of the AMS 58(3):434-437.
Billey, S.C., and B.E. Tenner. 2013. Fingerprint databases for theorems. Notices of the AMS 60(8):1034-1039.
Bosch, A., A. Zisserman, and X. Muoz. 2007. Image classification using random forests and ferns. Pp. 1-8 in IEEE 11th International Conference on Computer Vision. doi:10.1109/ICCV.2007.4409066.
Buchberger, B. 2006. Bruno Bucherger’s PhD thesis: 1965: An algorithm for finding the basis elements of the residue class ring of a zero dimensional polynomial ideal. Journal of Symbolic Computation 41(3-4):475-511.
Cox, D., J. Little, and D. O’Shea. 1997. Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra. Springer, New York.
Ganiz, M.C., W.M. Pottenger, and C.D. Janneck. 2005. Recent Advances in Literature-Based Discovery. Technical Report LU-CSE-05-027. Lehigh University, Bethlehem, Pa.
Heller, S., A. McNaught, S. Stein, D. Tchekhovskoi, and I. Pletnev. 2013. InChI the worldwide chemical structure identifier standard. Journal of Cheminformatics 5(7).
Hoffman, P. 1987. The man who loves only numbers. Atlantic Monthly 260(5):60.
Hirsch, J.E. 2005. An index to quantify an individual’s scientific research output. Proceedings of the National Academy of Sciences U.S.A. 102(46):16569-16572.
Jaynes, E.T. 2003. Probability Theory: The Logic of Science. Cambridge University Press.
Lee, R., and D.M. Wilczyñski. 1997. Representing homology classes by locally flat surfaces of minimum genus. American Journal of Mathematics 119:1119-1137.
Linnaeus, C. 1758. Systema Naturae per Regna Tria Naturae, secundum Classes, Ordines, Genera, Species, cum Characteribus, Differentiis, Synonymis, Locis [System of Nature through the Three Kingdoms of Nature, according to Classes, Orders, Genera and Species, with Characters, Differences, Synonyms, Places]. 10th edition. http://www.biodiversitylibrary.org/item/10277.
López-Cózar, E.D., N. Robinson-Garcia, and D. Torres-Salinas. 2013. “The Google Scholar Experiment: How to Index False Papers and Manipulate Bibliometric Indicators.” http://arxiv.org/abs/1309.2413.
Lowe, D. 2004. Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision 60(2):91-110.
MacGillivray, M. Open Citations—Doing Some Graph Visualisations. Open Citations blog. Posted on March 28, 2013. http://opencitations.wordpress.com/2013/03/28/open-citations-doing-some-graph-visualisations/.
Renschuch, B., H. Roloff, and G.G. Rasputin. 1987. Contributions to Constructive Polynomial Ideal Theory XXIII: Forgotten Works of Leningrad Mathematician N.M. Gjunter on Polynomial Ideal Theory. Wiss. Z. d. Pädagogische Hochschule Potsdam 31:111-126. Translated by Michael Abramson, ACM SIGSAM Bulletin 37(2), June 2003.
Sojka, P., and M. Líška. 2011. Indexing and searching mathematics in digital libraries. Pp. 228-243 in Intelligent Computer Mathematics. Lecture Notes in Computer Science, Volume 6824. Springer Berlin Heidelberg.
Suzuki, N. 2013. “The Chern Character in the Simplicial de Rham Complex.” http://arxiv.org/abs/1306.5949.
Swanson, D. 1986. Fish-oil, Raynauds Syndrome, and undiscovered public knowledge. Perspectives in Biology and Medicine 30(1):718.
Swanson, D. 1987. Two medical literatures that are logically but not bibliographically connected. Journal of the American Society for Information Science 38(4):228233.
Ulam, S. 1957. Masian Smoluchowski and the theory of probabilities in physics. American Journal of Physics 25:475-481.
von Ahn, L. 2011. “Massive-scale Online Collaboration.” TED Talk (video). http://www.ted.com/talks/luis_von_ahn_massive_scale_online_collaboration.html.
Wiedijk, F. 2007. The QED manifesto revisited. Studies in Logic, Grammar, and Rhetoric 10(23):121-133. http://mizar.org/trybulec65/8.pdf.
Zwegers, S. 2008. “Mock Theta Functions.” http://arxiv.org/abs/0807.4834.



























