Measuring Up: Prototypes for Mathematics Assessment (1993)

Suggested time allotment

One class period

Student social organization

Students working alone or in pairs

Task

Assumed background: This task presents information in the form of a directed graph, which is a way of showing relationships among objects. In this case, the dots represent people; they are connected with arrows indicating a certain mathematical relation: an arrow from A to B means ''A won the game that A and B played." Some groups of children, for example ones that use the Comprehensive School Mathematics Program (McREL, 1992), will be familiar with a similar notation, and hence will need little teacher introduction. The task, however, does not assume familiarity with the notation. (Clearly it would be inappropriate to use this task to compare classes to whom this notation is familiar with classes to whom it is not.)

Children should have had some prior experience in "translating" from one

symbolic representation of a situation to another. In this case, the directed graph representation is to be transformed into a list of players ordered on the basis of their tournament records so far.

Presenting the task: If students are not already familiar with the directed graph notation, the teacher should introduce it (without the terminology "directed graph") as a means of displaying information about four students in a Tic-Tac-Toe tournament.

The teacher should explain the situation and ask simple questions such as:

Student assessment activity: The teacher should pass out copies of the student sheet and read through the introduction and question 1, to be sure that everyone has an understanding of the meaning of the dots and the arrows. A Spanish translation of the task appears immediately following the English version.

Name ________________________________________ Date _____________

Six children are in a checkers tournament. The figure below shows the results of the games played so far.

(Remember, in the picture, an arrow like

means that José won his game against Alex. The arrow always points from the winner to the loser.)

1. Who won the game between Pat and Robin? _____

2. Which children has Lee already played against? ______

3. Which of those games did Lee win? ______

4. How many games have been played by the children so far? _____ Explain how you know.

5. Make a table showing the current standings of the six children. Put the player who has won the most games in first place, at the top. If two players are tied, they can be listed in either order.

6. The tournament will be over when everybody has played everybody else exactly once. How many more games need to be played to finish the tournament? ______ Explain your answer.

7. Dana and Lee have not played yet. Who do you think will win when they play? ______ Explain why you think so.

Nombre ________________________________________ Fecha _____________

Seis niños participan en un torneo de Damas. El dibujo representa los resultados de los partidos que han sido jugados hasta el momento.

(Recuerda que en el dibujo una flecha como esta

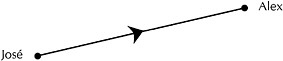
significa que José le ganó el partido a Alex. La flecha siempre senala del ganador al perdedor.)

1. ¿Quién ganó el partido entre Pat y Robin? ______

2. ¿Contra qué niños ya ha jugado Lee? ______

3. ¿Cuál o cuáles de esos partidos ganó Lee? ______

4. ¿Cuántos partidos en total han jugado todos los niños hasta el momento? ______ Explica tu contestación.

5. Haz una tabla que demuestre la posición de los seis niños. Coloca al jugador o jugadora que ha ganado la mayor cantidad de partidos en el primer lugar; en la primera línea. Si hay un empate entre dos jugadores, puedes colocarlos en cualquier orden.

6. El torneo terminará cuando todo el mundo haya jugado contra todo el mundo exactamente una vez. ¿Cuántos partidos faltan por jugar para que el torneo termine? Explica tu contestación.

7. Dana y Lee no han jugado todavía. ¿Quién crees que ganará cuando jueguen? ______ Explica el por qué tu piensas así.

The content involved in this task is the elementary use of a network in graph theory to present a familiar situation. Such mathematics broadens the curriculum usually thought appropriate for the fourth grade. Yet the task is linked to more traditional material as students are asked to convert the graphical representation to a familiar ranked table, thus illustrating the connections between such different representations. The last two questions, in particular, allow a variety of strategies to be applied. Students must use analytical skills and demonstrate reasoning to answer the questions, two fundamental attributes of mathematical power. In addition, the task shows that mathematics can be non-computational.

One interesting feature of this task is that it requires children to count sets of objects (the games that have been played and the games that have yet to be played) when it is not immediately clear how these objects are represented in the given picture. Students are thus asked to explore a very basic notion — counting, in this instance — in a new context. When counting the games that have been played, the student may realize that each of the six players has played three games, because there are three arrows associated with each dot; nonetheless, it is not true that 18 games have been played. (The student must see the one-to-one correspondence between the arrows and the games, and devise a way to count the arrows properly, keeping track of which arrows have been counted and which have not, or simply realize that each game has a winner and loser, and divide 18 by 2.) It is even more challenging to count the games that have not yet been played.

Task design considerations: Note that the relation "X beats Y in a game of checkers" is not transitive; that is, if X beats Y and Y beats Z, then it is not necessarily the case that X beats Z. In fact, the games were deliberately arranged so that one trio of players illustrates this: José beat Alex and Alex beat Lee, but José did not beat Lee.

An earlier version of question 6 was phrased as "How many games need to be played to finish the tournament?" This was found to be somewhat ambiguous; it could mean either "How many games in all are needed?" or "How many more

games are needed?" Children in a pilot test interpreted the question in both ways. Because there was nothing to be gained by the ambiguity, it is now "How many more games need to be played to finish the tournament?"

The Spanish translation of the task is included to highlight the need for assessment designers and teachers to be sensitive to the nuances of language. This translation, like the one of the Taxman task, has been done in the informal form. Some students (for example, those from Costa Rica) will not be used to this form. Also, note that question 3, "Which of those games did Lee win?" has been translated as "¿Cuál o cuáles de esos partidos ganó Lee?" Using only "cuál" or "cuáles" by itself would prejudge the situation by telling the student whether there is one game or more than one.

Variants and extensions: Several variants come to mind immediately. One can add players, add or change the directions of the arrows, and ask other kinds of questions — for example, "If there were 7 players, how many games would there be if everyone played everyone else exactly once?"

One can extend the setting to relations that are transitive — for example, an arrow pointing from A to B means that "A is taller than B." This relation, unlike the one in this task, is transitive, and so one can infer that if there are arrows from A to B and from B to C, then there must be an arrow from A to C.

Indeed, there are dozens of variations on the theme of presenting information about relations among objects through the use of arrow diagrams (directed graphs). These objects can be numbers, geometric figures, or other mathematical entities, as well as people.

Characteristics of the high response:

The high-level response is one that shows an understanding of the situation as a whole — what the various components of the directed graph represent, and how that representation relates to the other representation.

One expects that all answers will be correct. In question 4, the justification for asserting that 9 games have been played so

far is something to the effect that (a) there are 9 arrows or that (b) each of 6 players has competed in 3 games, which means a total of 18 wins and losses. Since each game produces a win and a loss, there must have been 9 games.

Note that in question 5, ties arise for 2nd and 3rd places in the ranking, as well as for 4th and 5th. Therefore, either order within those pairs is correct.

In question 6, the correct answer, 6, can be obtained by enumerating the pairs who have not played. Alternately, the child may see that there will be a total of 15 games, and, since 9 have been played, 6 remain.

In question 7, the rationale could be any of the following:

1. Since Dana beat Alex and Alex beat Lee, I think Dana will beat Lee.

2. Since both Dana and Lee have identical 2-1 records, we cannot predict who will win.

3. Dana and Lee have identical 2-1 records, but Dana lost to Pat, the best player at 3-0, while Lee lost to José, whose record is only 1 win, 2 losses. Therefore, Dana seems to be the stronger player, and so I think Dana will win.

If one were to make finer distinctions within the "high" category, it is important to note that response a, above, makes an argument that is not fully justified by the situation. As already mentioned, the relation is not transitive, and hence the outcome of the Dana-Lee game is not necessarily a win by Dana. So "I think Dana will beat Lee" is a better response than simply "Dana will beat Lee."

Characteristics of the medium response:

The student can interpret the meaning of individual arrows correctly and can determine how many games have been played so far. Thus questions 1 through 4 are mostly answered correctly. The response to question 5, however, indicates difficulty in connecting the arrow-diagram notation with the table showing the standings of the players. One or two pairs of names may be in the incorrect order.

In question 6, the child may erroneously conclude that a total of 30 games will be played (6 people, 5 games each) and hence give an answer of 21. This answer shows greater insight than one that is closer to the correct answer but was obtained by incorrectly counting the missing arrows.

The rationale offered in question 7 is based on a correct interpretation of some of the information presented in the

arrow diagram, but does not present any kind of complete argument. For example, the student may say something like, ''Dana, because Dana beat Alex," or "Lee, because Lee beat two people," or "You can't tell, because they both lost to Robin."

Characteristics of the low response:

Questions 1 through 3 are answered correctly. However, there is little awareness of the relationship between the arrows in the diagram and the games that have been played. Hence responses to questions 4 through 6 are incorrect or lack any kind of justification.

The response to question 7 may be based on subjective feelings that have no basis in the information supplied in the arrow diagram. For example, the child may say something like "Dana, because I think she's better."

Mid-continent Regional Educational Laboratory (1992). Comprehensive School Mathematics Program. Aurora (CO): Author.