Appendix F
Empirical Equation for Estimating Ocean Acidification
This appendix provides the supporting material for estimating the pH of seawater that may be required for the climate change damage estimates discussed in Chapter 5. It covers two approaches consistent with the simple Earth system model detailed in Chapter 4. The first approach estimates globally averaged pH directly from globally averaged atmospheric CO2. The second approach estimates pH from surface temperature and the ocean carbon concentrations and may be useful for estimating regional changes in pH or global changes in pH in SC-CO2 models with interactive ocean carbon modules. In both approaches, regression relationships are derived from outputs from a full ocean carbonate chemistry code run for typical ranges of ocean seawater temperatures, dissolved inorganic carbon concentrations, and chemical compositions. This allows applying the standard set of equations to both global and regional estimates of pH.
OVERVIEW
Carbonate chemistry in the ocean comprises mainly two reversible reactions:
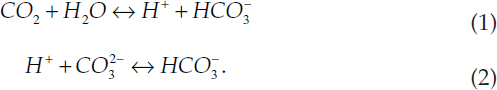
The reactions are governed by the 1st and 2nd dissociation constants of carbonic acid, both of which vary with temperature and salinity:
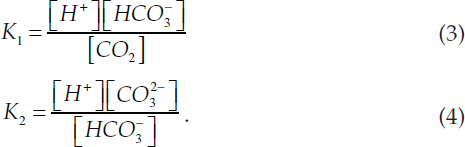
The reversible reactions (1) and (2) must conserve mass of dissolved inorganic carbon (DIC) and charge. Charge balance is represented by total alkalinity (AT), which is the number of moles of hydrogen ion equivalent to the excess of proton acceptors over proton donors in 1 kg of sample (Dickson, 1981):
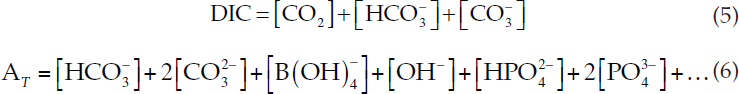
For given values of DIC and AT, equations (3), (4), (5), and (6) are four equations in four unknowns and can be solved iteratively.
To derive the empirical relationships describing the dependence of pH on temperature and carbon concentration, the publicly available carbonate chemistry code CO2SYS.m is used (van Heuven et al., 2011). Temperature-dependent solubility is from Weiss (1974); equilibrium constants K1 and K2 are from Luecker et al. (2000); and those for the species in AT (boric acid, hydrogen fluoride, phosphoric acid, and silicic acid) are from Dickson et al. (2007). The globally averaged AT for the upper 100m is 2311 microeq/kg seawater, based on the GLODAP2 gridded data (Key et al., 2004). The concentration of borates varies linearly with salinity, and it is 415.7 micromol/kg for the Luecker et al. (2000) equilibrium constants. Other standard ocean values are S = 35 psu, and the concentrations of silicate and phosphate are 50 and 2 micromol/kg, respectively. The code CO2SYS.m was run for concentrations of DIC ranging from 1800 to 2300 micromol/kg seawater, and for surface temperatures ranging from 0 to 50°C. Outputs pH and the partial pressure of CO2 in surface water (pCO2) are used for regression analyses below.
APPROACH 1: GLOBALLY AVERAGED PH
The concentration of hydrogen ion is directly related to the concentration of CO2 solution (see Equation [1], above), and a simple relationship between pH and the partial pressure of pCO2 can be derived:
![]()
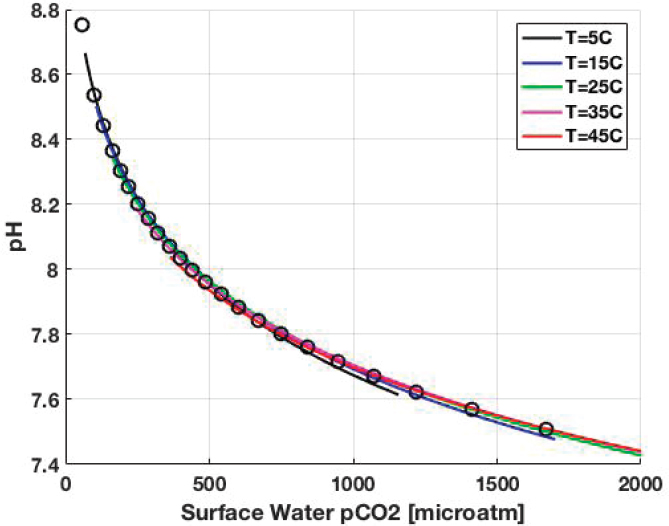
where pH = −log10[H+] is defined on the “total” hydrogen ion scale (Dickson et al., 2007) and pCO2 is in micro-atmospheres.1Figure F-1 shows that pH estimated by Equation (7) closely matches that calculated by CO2SYS.m for various temperatures. Temperature dependence has been subsumed into the determination of pCO2.
Globally averaged pCO2 of the surface ocean can be estimated from globally averaged CO2 concentration in the atmosphere with approximately 1 year lag.
__________________
1 An atmospheric CO2 concentration of 400 ppm (10–6 mol CO2 per mol air) is equivalent to an atmospheric CO2 partial pressure of 400 microatm.
APPROACH 2: REGIONAL PH
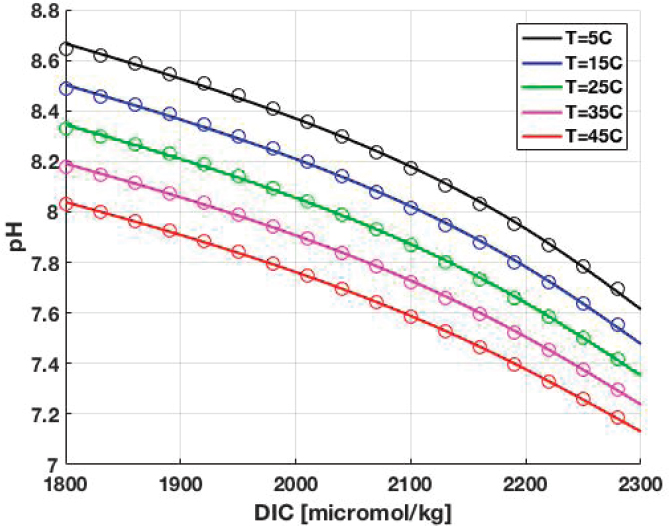
Temperature, DIC, and hence pCO2 and pH of the surface ocean vary from place to place and from season to season. Results from CO2SYS.m show the variations of pH as a function of DIC and temperature: see Figure F-2. As can be seen, pH decreases with increasing dissolved inorganic carbon and with increases temperature.
The committee derived empirical fits to the results shown in Figure F-2. DIC is in micromol/kg seawater, and T is temperature in Celsius.
![]()
with
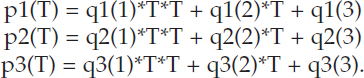
| i = 1 | i = 2 | i = 3 | |
| q1(i) | 1.32165e-10 | 1.52051e-08 | –2.37923e-06 |
| q2(i) | –4.82195e-07 | -5.89841e-05 | 7.69483e-03 |
| q3(i) | 4.59338e-04 | 4.05966e-02 | 2.58590e+00 |
The pH values calculated using Equation (7) are shown as circles in Figure F-1.
ESTIMATION OF DIC INCREASE
These calculations assume2 the preindustrial near-surface ocean has DIC0 = 2005 micromol/kg and T0 = 15°C. For an increase of X Pg CO2 in the upper ocean box of volume V (m3), the change in DIC can be estimated from:
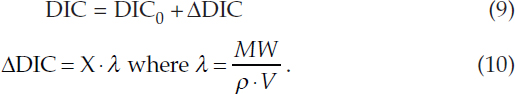
In Equation (10), MW = 1021/44 micromol/PgCO2 is the molecular weight of CO2 and ρ = 1024 kg/m3 is the density of seawater. For a 100 m deep global ocean box, λ = 0.634. For alternative upper-ocean volumes, λ will require a recalibration to be consistent with the transcient climate response and equilibrium climate sensitivity estimates that implicitly include a heat capacity estimate as given in FAIR or the SC-IAMs.
__________________
2 See http://www.whoi.edu/OCB-OA/page.do?pid=112136 [November 2016].
REFERENCES
Dickson, A.G. (1981). An exact definition of total alkalinity and a procedure for the estimation of alkalinity and total inorganic carbon from titration data. Deep Sea Research, 28A, 609-623.
Dickson, A.G., Sabine, C.L. and Christian, J.R. (Eds.). (2007). Guide to Best Practices for Ocean Co2 Measurements. PICES Special Publication 3. Sidney, British Columbia: North Pacific Marine Science Organization.
Key, R.M., Kozyr, A., Sabine, C.L., Lee, K, Wanninkhof, R., Bullister, J., Feely, R.A., Millero, F. Mordy, C., and Peng. T.-H. (2004). A global ocean carbon climatology: Results from GLODAP. Global Biogeochemical Cycles, 18, GB4031. Available: http://cdiac.ornl.gov/ftp/oceans/GLODAP_Gridded_Data [November 2016].
Lueker, T.J., Dickson, A.G., and Keeling, C.D. 2000. Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: Validation based on laboratory measurements of CO2 in gas and seawater at equilibrium. Marine Chemistry, 70, 105-119.
Van Heuven, S., Pierrot, D., Rae, J.W.B., Lewis, E., and Wallace, D.W.R. (2011). MATLAB Program Developed for CO2 System Calculations. ORNL/CDIAC-105b. Oak Ridge, TN: U.S. Department of Energy.
Weiss, R.F. (1974). Carbon dioxide in water and seawater: The solubility of a non-ideal gas. Marine Chemistry, 2, 203-215.






