Page 147
Chapter 10
Magnetic Source Imaging
10.1 Introduction
Ion currents arising in the neurons of the heart and the brain produce magnetic fields outside the body that can be measured by arrays of SQUID (superconducting quantum interference device) detectors placed near the chest or head; the recording of these magnetic fields is known as magnetocardiography (MCG) or magnetoencephalography (MEG). Magnetic source imaging (MSI) is the reconstruction of the current sources in the heart or brain from these recorded magnetic fields. These fields result from the synchronous activity of tens or hundreds of thousands of neurons.
Both magnetic source imaging and electrical source imaging (see Chapter 8) seek to determine the location, orientation, and magnitude of current sources within the body. The magnetic field at the surface is most strongly determined by current sources directed parallel to the surface, but the electrical potentials are determined by current sources directed perpendicular to the surface. Other than the signal distortion from the heterogeneity of tissue conductivity, there is no clear physical reason that the clinical information produced by biomagnetic measurements could not as well be obtained from electrical potential mapping. An advantage of MSI over ESI is that all body tissues are magnetically transparent and the magnetic fields propagate to the surface without distortion. The electrical potentials at the surface, on the other hand, are distorted by variations in conductivity within the body; this is especially true in the head, where the low conductivity of the skull both distorts and hides the electrical activity of the brain. A disadvantage of MSI is that the need for cryogenic cooling and a magnetically shielded
Page 148
room makes the procedure cumbersome with the present technology.
Biomagnetism offers a tool to study processes where electrical function is important. Promising results have been obtained in the fields of cardiology and epilepsy. Sites of origin for heart arrhythmias (e.g., the accessory path for Wolff-Parkinson-White syndrome) can be identified by electrical activity in abnormal anatomical locations. Non-invasive localization allows treatment by guiding an ablation catheter directly to the correct site. MSI can also be used in the surgical treatment of intractable epilepsy to locate the epileptigenic focus and functional areas of the brain that must be conserved during surgery. A potential use in neuroscience is the spatial and temporal study of functional processing areas in the brain in response to auditory, visual, and somatosensory stimuli. Biomagnetism also offers a research tool for studying schizophrenia as well as Parkinson's and Huntington's syndromes. The function of peripheral nerves can be studied, and prenatal magnetocardiography can be carried out.
A major strength of MSI is that it can resolve events separated by milliseconds, whereas other methods such as functional magnetic resonance imaging (fMRI), magnetic resonance spectroscopy (MRS), positron emission tomography (PET), and single photon emission computed tomography (SPECT) have time resolutions of seconds to many minutes, depending on the information sought. A weakness of MSI is that any magnetic field distribution on the surface of the head can be explained by an infinite number of current distributions inside the head. Thus, a successful source analysis is dependent on the availability of additional information suitable for constraining the inverse problem to be solved.
Because of their extreme weakness, on the order of femto-teslas, biomagnetic fields require sensitive sensors. Up to now only superconducting quantum interference devices (SQUIDs) have been able to achieve the required sensitivity below ![]() . In order to separate the biomagnetic fields from much larger external interferences, screening chambers made from soft magnetic and conductive material are necessary. The two technical areas most in need of development are simplification of the detector array and creation of methods to remove interference without the use of an expensive (e.g., $500,000) enclosure. An active screen applying a closed control loop with a sensor for the interfering field and compensating current loops could be an attractive alternative to the passive screen.
. In order to separate the biomagnetic fields from much larger external interferences, screening chambers made from soft magnetic and conductive material are necessary. The two technical areas most in need of development are simplification of the detector array and creation of methods to remove interference without the use of an expensive (e.g., $500,000) enclosure. An active screen applying a closed control loop with a sensor for the interfering field and compensating current loops could be an attractive alternative to the passive screen.
SQUIDs based on high-temperature superconductor technology could operate with inexpensive liquid nitrogen. Current technology has already led to devices with a sensitivity of about ![]() , which is still an order of
, which is still an order of
Page 149
magnitude above that achieved with ''classic" superconductivity. It is likely, however, that further improvements are possible.
10.2 Mathematical Considerations
The inverse problem of calculating the current density J(p) within the body as a function of position p from the magnetic field B(r) is defined by the Biot-Savart law,
![]()
See also section 14.1.9.
The current distribution within the body consists of two components: a non-ohmic primary (or impressed) current that is directly related to the physiological processes, and a volume current induced by the primary current sources in the conductive body tissue. Since the body is moderately conductive, the current sources being imaged generate "volume currents" within the body that depend on the body geometry and the distribution of tissue conductivity. These volume currents generate their own magnetic fields and thereby modify the fields generated by the primary current sources themselves. Accounting for the effects of these volume currents improves the accuracy of the reconstruction. In some simple geometries, it can be shown that the volume currents have no effect on the magnetic field outside the body and thus can be ignored; this is the usual assumption for contemporary implementations of MSI in commercial and research instruments. But for realistic body geometries, the effect of the volume currents must be included for an accurate reconstruction. General models allowing anisotropic conductivity have been studied using finite-element or finite-difference methods, but at present these techniques require much computation time and are not yet practical. Given a primary current distribution JP(p), the electrical potential X can be computed by solving Poisson's equation
![]()
with the boundary condition that n · Ñf = 0 on the body surface. The conductivity o must be known as a function of position and may be determined by a prior magnetic resonance scan. Then the total current J is given by Ohm's law
![]()
Page 150
These equations can be solved by various finite-element and boundary-element methods.
Given the magnetic field as a function of position, the magnetic flux ym threading a coil of area Am is simply the surface integral
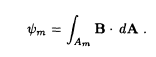
The fact that reasonable localization results for dipolar sources can often be obtained with extremely simplified models (e.g., a homogeneous sphere) suggests that relatively simple volume conductor models (e.g., a piecewise homogeneous volume conductor) might suffice to provide localization accuracies of the order of millimeters. However, volume conductor models with more complicated properties (e.g., anisotropic conductivities) represent no major problems.
10.3 Source Models
Because contemporary SQUID detector arrays do not provide sufficient information to estimate the underlying source configuration in a unique way, any interpretation of magnetic field data requires certain assumptions. In most studies the assumption is made that only a single source is active at a given time point and that the spatial extent of the source is small compared to the distances between source and measurement locations. The resulting model is the equivalent current dipole. Even though the assumption of a single dipole is generally an oversimplification, a source analysis based on this model can provide at least an estimate of the center of the source and of the mean activity in the source. A straightforward extension of the single dipole model is the multidipole model, with two or more spatially separated equivalent current dipoles. Model simulations have shown that two simultaneously active dipoles can be separated only if the spacing of the dipoles is comparable to the distances between the dipoles and measurement locations. Higher spatial resolution can be expected if time intervals rather than single time points are considered.
The single-source model assumes that the observed fields are generated by a few point sources (typically current dipoles) and seeks to determine the position, orientation, and magnitude of these dipoles from the observed
Page 151
fields. That is, the unknown current distribution is written in the form
![]()
where the amplitude an , position pn, and orientation qn of each source are unknowns to be determined in the reconstruction. Since the fields depend nonlinearly on the dipole position and orientation, iterative optimization algorithms are required; such iterative algorithms are expensive in computer time and often find local rather than global minima. These methods work reasonably well for source models with one or perhaps two dipoles but rapidly become more expensive to compute and less reliable as the number of dipoles increases.
An alternative to single and multiple dipoles is a diffuse current distribution, which can be discretized in terms of a large number of homogeneously distributed current dipoles. Models of this type have the advantage that the source structure need not be defined in advance. However, the number of model parameters is generally much larger than the number of measurement points, and so a solution has to be selected among an infinite number of possible solutions. Choosing the current density with the smallest root mean square (the "minimum norm solution") gives a three-dimensional image that depends on the choice of regularization technique or source model.
This approach assumes that the observed fields are generated by a distributed current source and then approximates that source as a weighted sum of elementary sources that are fixed in position; then it is necessary only to find the weights (or source amplitudes) that best approximate the observations. That is, the unknown current distribution is written in the form
![]()
where the position pn and orientation qn are fixed in advance, leaving only the amplitudes an to be determined in the reconstruction. The elementary sources are often dipoles, but other distributed sources may also be used. Fixing the source positions reduces the problem to one in which there is a unique global minimum. The observed magnetic flux measurements are linear in the unknown amplitudes, or
![]()
Page 152
where y is a vector of magnetic flux measurements, a is a vector of the unknown source amplitudes, and F is the forward transfer matrix connecting them. Iterative solution is not required, and the solution can be rapidly computed by numerical linear algebra software.
In sum, three paths can be pursued: (1) a single source can be reconstructed with rather high spatial resolution; (2) distributed current densities can be reconstructed with poor spatial resolution; or (3) several independent single sources can be identified from the time course of the magnetic field and reconstructed similar to a single source. All three methods require a model of the conductivity distribution of the head or torso under investigation. If this is taken from individual three-dimensional medical images, significant computational efforts are required.
10.4 Resolution
The limited number of detectors and the low signal-to-noise ratio means that MSI has poorer spatial resolution (1-2 cm) than do many other medical imaging modalities; furthermore, depending on the source strength, sources in the brain must be within several centimeters of the surface to be reliably detected; sources in the heart are stronger and deeper sources can be detected there. The temporal resolution of MSI, however, is milliseconds or tens of milliseconds, which makes it attractive for neuroscience studies.
A current line of research is to improve the apparent spatial resolution of MSI by using prior knowledge of the anatomy obtained from magnetic resonance imaging (MRI) or computed tomography (CT) to constrain the magnetic source reconstruction. One approach is simply to superimpose reconstructed dipole solutions on a magnetic resonance image registered to the same coordinate system; dipole locations not consistent with the anatomy may then be rejected as artifacts. This has been done with dipole point sources and is useful in interpreting the reconstruction.
A more sophisticated approach is to constrain the reconstruction by permitting sources only where they are consistent with the anatomy. For example, sources in the skull and in the white matter would be rejected as inconsistent; the reconstruction would then be the set of sources and source amplitudes that best match the observations and are consistent with the anatomy. This approach has promise for future development.
Such constrained reconstructions have been demonstrated by computer simulation for distributed source models, where they can be easily imple-
Page 153
mented by excluding elementary sources inconsistent with the anatomy. The particular algorithms used can also incorporate prior information about the expected amplitude of the sources, expected amplitude of the detector noise, and spatial and temporal correlations between sources. The use of such prior knowledge has been demonstrated in computer simulation to improve the accuracy of the reconstructed source distribution. One potential problem is that true source distributions inconsistent with the assumed prior distributions can generate reconstruction artifacts such that the reconstruction with priors is less accurate than the reconstruction with no priors.
10.5 Summary
As with electroencephalography and electrocardiology, clinical and scientific applications of MSI await the development of less expensive instrumentation as well as practical computational strategies for determining the spatial distribution of the current generators in the brain and heart. The steady improvement in this technology has been mostly through development of larger arrays of SQUID detectors. Refinements in applied mathematical approaches are probably less important than improvements in computational practicality. The latter presents the greatest challenge.
10.6 Research Opportunities
· For magnetic source imaging to become an acceptable procedure, the cost of biomagnetic instrumentation must first be reduced. The most expensive component is the screening against external interference, given that the necessary soft magnetic material requires a costly manufacturing process. Signal processing algorithms to suppress such interference are available and can be improved, but they may not be sufficient to completely obviate the need for shielding.
· Point and distributed source reconstructions are both approximations of the true distribution of current in the body, but it is not known which is a better approximation. The two types of reconstructions are so different that it is difficult to directly compare their accuracy. It would be beneficial to find some effective method of comparison.
· The incorporation of realistic body geometry and conductivity distributions used in the forward models is an important focus for study.
Page 154
As models become more detailed, they also become more expensive to compute, and additional research in the designs of efficient algorithms is likely to be useful. One question of particular interest is how accurate the forward model must be to yield accurate reconstructions from data with some specified noise level; since improved accuracy costs more computer time, it is preferable to use a forward model that is no more accurate than necessary.
· Existing distributed source models can exploit prior information about the expected source amplitudes and both spatial and temporal correlations between sources. It is not known, however, what values should be adopted for these prior distributions to optimize the trade-off between improved accuracy and an increased risk of artifacts. Reconstruction methods using prior information can create reconstruction artifacts when the true source distribution is inconsistent with the assumed priors. Methods are needed for detecting when priors are inconsistent with the data.
10.7 Suggested Reading
1. Ahonen, A.I., Hamalaiinen, M.S., Kajola, M.J., Knuutila, J.E.T., Laine, P.P., Lounasmaa, O.V., Simola, J.T., Tesche, C.D., and Vilkman, V.A, A 122-channel magnetometer covering the whole head, in Proceedings of the Satellite Symposium on Neuroscience and Technology of the 14th International Conference of the IEEE Engineering in Medicine and Biology Society, A. Dittmar and J.C. Froment, eds., Lyon, 1992, 16-20.
2. Bertrand, O., Thevenet, M., and Perrin, F., 3D finite element method in brain electrical activity studies, in Biomagnetic Localization and 3D Modelling, J. Nenonen, H.M. Rajala, and T. Katila, eds., Helsinki University of Technology, Department of Physics, Report TKK-F-A689, Helsinki, 1991, 154-171.
3. Cohen, D., Cuffin, B.N., Yunokuchi, K., Maniewski, R., Purcell, C., Cosgrove, G.R., Ives, J., Kennedy, J., and Schomer, D., MEG versus EEG localization test using implanted sources in the human brain, Ann. Neurol. 28 (1990), 811-817.
4. Hiamalainen, M.S., and Sarvas, J., Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data,
Page 155
IEEE Trans. Biomed. Eng. BME-36 (1989), 165-171.
5. Hughett, Paul, An optimal constrained linear inverse method for magnetic source imaging, Ann. Biomed. Eng., accepted for publication.
6. Ioannides, A.A., Bolton, J.P.R., and Clarke, C.J.S., Continuous probabilistic solutions to the biomagnetic inverse problem, Inverse Problems 5 (1989), 999-1012.
7. Kaufman, Lloyd, Kaufman, James H., and Wang, Jia-Zhu, On cortical folds and neuromagnetic fields, Electroencephalogr. Clin. Neurophysiol. 79 (1991), 211-226.
8. Liitkenh6ner, B., On the biomagnetic inverse procedure's capability of separating two current dipoles with a priori known locations, in Advances in Biomagnetism: Clinical Aspects, Excerpta Medica, M. Hoke, S.N. Ern6, Y.C. Okada, and G.L. Romani, eds., Amsterdam, 1992, 687-692.
9. Menninghaus, E., Liitkenhoner, B., Gonzalez, S.L., Hampson, S., and Pantev, C., Localization of a dipolar source in a skull phantom: Comparison between boundary element model and spherical model, in Proceedings of the Satellite Symposium on Neuroscience and Technology of the 14th International Conference of the IEEE Engineering in Medicine and Biology Society, A. Dittmar and J.C. Froment, eds., Lyon, 1992, 119-122.
10. Moran, J.E., Jacobson, G.P., and Tepley, N., Finite difference field mapping, in Advances in Biomagnetism: Clinical Aspects, Excerpta Medica, M. Hoke, S.N. Erne, Y.C. Okada, and G.L. Romani, eds., Amsterdam, 1992, 801-805.
11. Nenonen, J., Purcell, C.J., Horacek, B.M., Stroink, G., and Katila, T., Magnetocardiographic functional localization using a current dipole in a realistic torso, IEEE Trans. Biomed. Eng. BME-38 (1991), 658-664.
12. Purcell, Christopher J., and Stroink, Gerhard, Moving dipole inverse solutions using realistic torso models, IEEE Trans. Biomed. Eng. BME38 (1991), 82-84.
13. Ribary, U., Ioannides, A.A., Singh, K.D., Hasson, R., Bolton, J.P.R., Lado, F., Mogilner, A., and Llinas, R., Magnetic field tomography
Page 156
(MFT) of coherent thalamo-cortical 40-Hz oscillations in humans, Proc. Natl. Acad. Sci. USA 88 (1992), 11037-11041.
14. Stroink, Gerhard, Cardiomagnetic imaging, in Frontiers in Cardiovascular Imaging, Barry L. Zaret, Leon Kaufman, Alan S. Berson, and Rosalie A. Dunn, eds., 161-177, Raven Press, New York, 1993.
15. Wang, Jia-Zhu, Williamson, Samuel J., and Kaufman, Lloyd, Magnetic source images determined by a lead-field analysis: The unique minimum-norm least-squares estimation, IEEE Trans. Biomed. Eng. BME-39 (1992), 665-675.










