Page 133
Chapter 8
Electrical Source Imaging
8.1 Introduction
Electrical source imaging (ESI) is an emerging technique for reconstructing brain or cardiac electrical activity from electrical potentials measured away from the brain or heart. The concept of ESI is to improve on electroencephalography (EEG) or electrocardiography (ECG) by determining the locations of sources of current in the body from measurements of voltages. ESI could improve diagnoses and guide therapy related to epilepsy and heart conduction abnormalities through its capability for monitoring the effects of drugs or for locating an electrical abnormality that is to be removed.
Differences in potential within the brain, heart, and other tissues reflect the segregation of electrical charges at certain locations within these three-dimensional conductors as nerves are excited, causing cell membrane potentials to change. While the potential measured at some distance from an electrical charge generally decreases with increasing distance, the situation is more complex within the body; generators of the EEG, for example, are not simple point-like charge accumulations but rather are dipole-like layers. Moreover, these layers are convoluted and enmeshed in a volume conductor with spatially heterogeneous conductivity. The particular geometry and orientation of these layers determines the potential distribution within or at the surface of the three-dimensional body.
The classical approach to studying brain electrical activity involves recognizing patterns in a set of waveforms showing voltage as a function of time, acquired from about 20 electrodes placed on the scalp. While frequency analysis methods can indicate probable Alzheimer's disease by the
Page 134

Figure 8.1. Left: The multielectrode (180 or 250) mapping vest for obtaining body surface potential
maps. Right: The geometry used in the definition of the Cauchy problem in electrocardiography.
abnormal distribution of spatial frequency bands (see Fig. 1.1), the true distribution of neuronal activity, knowledge of which could lead to more refined diagnoses, is masked or blurred by the conducting tissue layers between the central cortex and the electrodes.
Cardiac electrical activity is likewise spatially complex, and involves the propagation of excitation wave fronts in the heart. Standard electrocardiographic techniques such as electrocardiography (ECG) and vectorcardiography (VCG) are very limited in their ability to provide information on regional electrical activity and to localize bioelectrical events in the heart. In fact, VCG lumps all cardiac wave fronts into a single dipole located at the "center" of the heart and known as the "heart vector." Traditional ECG and VCG employ a small number of electrodes (6 or 12) to measure potentials from the body surface, and the patterns of electrical activity cannot give the information required for characterizing the electrical activity of the heart. Non-invasive electrocardiography requires simultaneous recordings of electrical potential from 100 to 250 torso sites in order to map the body surface potential. These body surface potential maps (BSPMs) reflect the regional time course of electrical activity of the heart, information that is important for clinical treatment; an example is localization of the accessory atrioventricular pathway in Wolff-Parkinson-White syndrome prior to surgical dissection or catheter ablation. Figure 8.1 shows a 180-electrode BSPM vest. The computer-controlled data acquisition system permits simultaneous recording from all 180 sites every millisecond throughout the cardiac cycle.
Body surface potential distribution is a very low resolution projection
Page 135
of cardiac electrical activity, and details of regional electrical activity in the heart cannot be determined merely from visual inspection of the BSPMs. A mathematical method of reconstructing endocardial potentials is greatly needed. The endocardial surface of the heart is accessible through catheterization procedures. Recently, multielectrode probes have been developed with 65-100 evenly distributed electrodes on their surface that do not occlude the ventricular cavity and thus can be used in the catheterization laboratory for clinical and basic medical science studies.
Since the probe electrodes are not in direct contact with the endocardium, the measured potentials can provide only a low-resolution reflection of the endocardial potentials, smoothed out by the high conductivity of the intracavitary blood. A mathematical procedure for computing the distribution of endocardial potential from the measured potentials over the catheter surface would, therefore, enhance resolution and permit the localization of electrical cardiac events during electrophysiology studies. With this procedure, detailed endocardial maps could be obtained in the catheterization laboratory on a beat-by-beat basis. Such a procedure would permit studies of arrhythmogenesis in intact animals and patients, including studies of mechanisms, dynamic changes (initiation, termination), and the effects of drugs. It would also permit an accurate determination, in the catheterization laboratory, of the site of origin of an arrhythmia prior to surgical or catheter ablation. This information could be obtained in a few minutes, and the recording time could be limited to one cardiac cycle (with no need for sequential recordings). As catheter ablation techniques are developed, an accurate determination of the arrhythmogenic site in the catheterization laboratory is the limiting factor to the successful implementation of the ablation procedure.
Both cerebral cortex and epicardial reconstructions require multielectrode mapping of electric potential on a closed surface (the scalp and torso, respectively).
8.2 Outline of ESI Reconstruction Methods
The reconstruction procedures described above are characterized mathematically as solutions to the inverse problem of electroencephalography and electrocardiography. The mathematical approach to both reconstruction procedures is the same and is outlined below with a focus on the torso-epicardium inverse problem. The same principles apply to the scalp-cortex problem of
Page 136
electroencephalography.
The inverse problem in electrocardiography, formulated in terms of epicardial potentials, constitutes the following Cauchy problem (see also section 14.1.10):
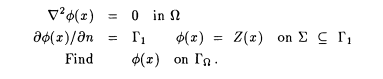
The geometry is defined in Figure 8.1 (right), f (x) is the potential in W, Z(x) is the (known) potential distribution on the torso, and ¶ f (x) /¶ n is the normal derivative of f (x) on Gl, which has to be zero since the normal component of current at the torso surface is zero. (The torso is in air, an insulating medium that does not support current flow.)
While a unique solution to this problem exists, the problem is ill posed in the sense that small perturbations in the data (noise) result in unbounded errors in the solution. This property implies that a straightforward solution is not possible because the data are never available without a certain degree of noise. Large deviations from the actual solution may result from inaccuracy of the data measurement, incomplete knowledge of the potential over the entire body surface, or an inaccurate description of the inhomogeneous torso.
The numerical solution for the inverse problem requires two steps. The first step is the construction of a mathematical expression describing the potential field throughout the torso volume conductor, particularly on the body surface, as a function of epicardial potential data (the forward problem). This has generally been done with either the finite-element method (FEM) or the boundary-element method (BEM). The second step is the inversion of that expression to enable the reconstruction of epicardial potentials from the measured torso potential data (the inverse problem). The following describes the methodology for each step.
8.2.1 Forward Problem
The BEM is a subset of the FEM, where the surface bounding the volume is divided into two-dimensional elements; each surface element has a basis function describing the distribution of electrical potential. While both the conductivity and the geometry of the volume are taken into account in the solution of the problem, only the relationships among the various regions
Page 137
of the surfaces appear in the final formulation. A major advantage of the BEM as compared to the FEM is that it involves fewer nodes (only the surface) and hence less overhead in construction and in modifying the mesh. Its major disadvantage is that its matrix is full and therefore requires more computer memory. With the capacity of the modern computer, however, this characteristic is not of great concern.
The BEM is derived from Green's second theorem:
![]()
In this expression the surface S includes the epicardial surface SE and the torso surface ST , and V is the homogeneous volume enclosed between the surfaces SE and ST . The scalar potential f satisfies Laplace's equation Ñ2f = 0 within the volume; hence, the second term on the left-hand side is zero. The variable r is the distance between a field point p and a source point q within that volume; 1/r is the Green's function or fundamental solution satisfying Poisson's equation at a point. ¶ /¶n is the normal derivative.
8.2.2 Inverse Problem
The inverse problem is formulated by dividing the brain cerebral cortex or epicardial surface SE into ME triangular elements and the torso surface ST into MT triangular elements. After manipulation and regrouping of terms, the following matrix equation is obtained:
![]()
where V E is the vector of cerebral cortex or epicardial potentials, V T is the vector of scalp or torso potentials, and A is the transfer matrix between heart and torso that depends on anatomic and electrical properties of hearttorso geometry. The inverse problem requires an inversion of A to give VE in terms of VT.
Inversion is performed with a least-squares approach, minimizing the residual vector with respect to V E, leading to the solution
![]()
where * refers to transpose.
Because eigenvalues of the matrix A are very small, (A* A)-1greatly magnifies whatever it multiplies. If V T contained the exact values of scalp or
Page 138
torso electric potential, this last equation would give an excellent estimate of the solution V E. However, any inevitable error term becomes greatly magnified, giving an erroneous (and sometimes unbounded) ''solution." Techniques of regularization must therefore be used to minimize the effects of such error by imposing constraints on the solution. Many of the regularization methods produce similar results and even reduce to similar forms for certain parameter values. The Tikhonov regularization method (see also section 14.4.1) has been found to give good results in this electrical mapping problem. V E is obtained by minimizing the objective function
![]()
where t is a regularization parameter and R is either the unit matrix I (Tikhonov method of order zero), the surface gradient operator G (Tikhonov method of first order), or the surface Laplacian operator L (Tikhonov method of second order). The solution now becomes
![]()
8.2.3 Temporal Regularization
The electrical mapping problem is also characterized by the fact that brain and cardiac activation is a continuous process in time. Incorporation of the continuous time progression into the regularization procedure has been done using Twomey regularization. Because of the continuity of the activation sequence in time, it is reasonable to expect that an estimate of the solution at one time can be made from the information at other time frames, and that this will improve the estimate and hence the quality and accuracy of the inverse-reconstructed heart potential map (e.g., Fig. 8.2).
Instead of imposing constraints on the magnitude of the solution or on its derivatives, the Twomey method minimizes the difference between the solution VE and some estimate of the solution, P. The objective function becomes
![]()
The solution to this new objective function is
![]()
Of course, the objective function reduces to the Tikhonov zero-order objective function when P = 0.
Page 139

Figure 8.2. Example of a completely non-invasive computation. Early QRS (110 ms into the cardiac cycle, right ventricular breakthrough). (A) Measured epicardial potentials. (B) Inverse-recovered epicardial potentials obtained by Tikhonov zero-order regularization. (C) Computation of the epicardial distribution with temporal regularization using inverse-computed (Tikhonov zero-order) epicardial potential distribution from the next time frame (112 ms) for the estimate vector P. Anterior potentials are on the left; posterior potentials are on the right. Maxima (+) and minima (-) values, contour lines, and intervals are in microvolts. Solid contour lines indicate positive potentials; broken contour lines indicate negative potentials. RE: relative error. Arrows in the maps identify the anterior minimum that reflects right ventricular epicardial breakthrough. (Modified from Oster, H.S., and Rudy, Y., The use of temporal information in the regularization of the inverse problem of electrocardiography, IEEE Trans. Biomed. Eng.BME-39 (1992), 65-75.)
Page 140
The estimate P of epicardial potentials at a given time frame can be constructed using information from other time frames, and the optimal method of generating this estimate from historical and future time frames is yet to be determined.
8.3 Research Problems and Opportunities
ESI is a promising modality, but the number and quantitative precision of the brain or torso measurements and the degree of understanding of the conductive paths may be insufficient to allow an accurate solution of the Cauchy problem. The following research areas need further development before the potential of ESI can be realistically gauged.
· The inverse computation of cerebral cortex and epicardial potentials requires knowledge of the geometries and conductivities of intervening tissues. It may not be practical, in an experimental or clinical setting, to even measure the position of each body surface electrode. Some convenient strategy of individual-specific anatomic measurement (e.g., by MRI) needs to be developed so that the true geometry and inhomogeneous conductivity can be incorporated into the reconstructions of potentials.
· Resolution needs to be improved to the point that details of conductive disturbances (e.g., areas of slow conduction in the heart) can be detected and localized. This could be achieved by modifying the mathematical formulation to incorporate higher-resolution temporal and spatial information into the regularization procedure. This would include development of fast algorithms for computing and displaying reconstructed information at close to real time.
· The accuracy of the inverse procedure is dependent on the number and position of the surface electrodes. Methods are needed to characterize the optimal number and positions for expected noise conditions.
· Although potentials can be reconstructed with good accuracy using Tikhonov inversion techniques, a significant improvement is achieved when the time progression is incorporated into the regularization procedure for the cardiac inverse problem. These techniques could be extended to allow similar improvements in studies of the brain and of heart activation.
Page 141
8.4 Suggested Reading
1. Balish, M., and Muratore, R., The inverse problem in electroencephalography and magnetoencephalography, in Magnetoencephalography, Susumu Sato, ed., Raven Press, New York, 1990.
2. Gisser, D.G., Isaacson, D., and Newell, J.C., Electric current computed tomography and eigenvalues, SIAM J. Appl. Math. 50 (1990), 16231634.
3. Gloor, P., Neuronal generators and the problem of localization in electroencephalography: Application of volume conductor theory to electroencephalography, J. Clin. Neurophysiol. 2 (1985), 327-354.
4. Law, S.K., Nunez, P.L., and Wijesinghe, R.S., High-resolution EEG using spline generated surface laplacians on spherical and ellipsoidal surfaces, IEEE Trans. Biomed. Eng. 40 (1993).
5. Messinger-Rapport, B.J., and Rudy, Y., Regularization of the inverse problem in electrocardiography: A model study, Math. Biosci. 89 (1988), 79-118.
6. Messinger-Rapport, B.J., and Rudy, Y., Non-invasive recovery of epicardial potentials in a realistic heart-torso geometry: Normal sinus rhythm, Circ. Res. 66 (1990), 1023-1039.
7. Oster, H.S., and Rudy, Y., The use of temporal information in the regularization of the inverse problem of electrocardiography, IEEE Trans. Biomed. Eng. BME-39 (1992), 65-75.
8. Pilkington, T.C., and Plonsey, R., eds., Engineering Contributions to Biophysical Electrocardiography, IEEE, New York, 1982.
9. Rudy, Y., and Oster, H.S., The electrocardiographic inverse problem, in High Performance Computing in Biomedical Research, T.C. Pilkington, B. Loftis, J.F. Thompson, S.L.-Y. Woo, T.C. Palmer, and T.F. Budinger, eds., CRC Press, Boca Raton, Fla., 1993, 135-155.
10. Webster, J.G., ed., Electrical Impedance Tomography, Adam Hilger, New York, 1990.










