6
Criteria for Assessing Aircraft-Pilot Coupling Potential
This chapter examines the status of existing and proposed criteria for assessing APC potential. For fixed-wing aircraft with modest stability augmentation and conventional, fully powered surface actuating systems, Category I PIO tendencies are arguably reduced to a negligible level for aircraft that meet the flying qualities requirements in MIL-F-8785C69 or that are included in the newer MIL-STD-1797A.70 Rotorcraft that meet the requirements of ADS-33D68 should also be resistant to APC events. These flying qualities requirements have been developed over a long period of time using ground and in-flight simulators and experimental, prototype, and operational aircraft. Aircraft parameters and parameter combinations that are sensitive indicators of PIO tendencies have been identified. In addition, pilot assessments that include potential for PIO as a key factor, such as the CH PR (Cooper Harper pilot rating) and PIOR (PIO rating) have been used in empirical studies. In other words, the likelihood of severe Category I PIOs is greatly reduced in aircraft with Level 1 flying qualities. However, Category II and III PIOs are not well covered in these military specifications. Further, the FAA has no equivalent requirements for PIOs of any category.
The control-system characteristics of modern aircraft equipped with FBW FCSs do not necessarily correspond to those of mechanical systems in every detail. Designers have considerable latitude to provide effective aircraft dynamics that are better in some respects than conventional features. Thus classical criteria may not necessarily apply directly to these designs. Perhaps criteria suitable for these configurations need to be substituted for the older criteria that may no longer apply. Or perhaps, to the extent that the specific
dynamic properties of a modern aircraft are similar to those of earlier aircraft, PIO-specific criteria should complement existing requirements. Design flexibility and features intrinsic to FBW technology allow—and may require—additional criteria for aspects of the FCS that are markedly different from conventional systems. As some of the more recent events attest, PIOs involving FBW aircraft are not confined to Category I.
This chapter begins with a discussion of the desirable features of APC criteria (i.e., some general prerequisites), providing a rationale for comparing existing and new criteria. Short reviews are then presented of some noteworthy candidate criteria that have been suggested recently.
Existing criteria have focused on PIOs much more than non-oscillatory APC events. Therefore, some serious non-oscillatory APC events that may be involved in closed-loop system divergences have not received in-depth consideration. In the vast majority of severe PIOs, attitude oscillations have been the dominant feature, although both linear and angular accelerations and other cues have also been identified as contributors in some cases. Indeed, the sometimes ambiguous record of predicting PIOs using fixed-base simulators is often cited as indirect evidence that acceleration cues are more important than had been thought. But even in most of the flight research that specifically addresses PIOs in detail, attitude has been considered the predominant cue.5 Some notable attempts have been made to include criteria involving path and acceleration cues as add-ons to a baseline in which attitude is dominant.48,66 As might be expected in an empirically based engineering discipline, a great deal of art is needed to cover many situations.48
A proper synthesis that includes the above factors cannot be formulated using currently available data and theory. In any event, such a synthesis would greatly exceed the scope of this study. Because attitude control remains at the core of PIO problems, either in its own right or as a key inner-loop constituent, and because most research has been devoted to attitude control, this assessment of APC criteria is focused on oscillatory APC events involving pitch and roll attitude control problems.
To meet the needs of the several technical communities concerned with these issues, the following reviews are presented in two parts: general overviews and more detailed treatments of topics of interest primarily to specialists. The more specialized segments include elementary quantitative examples in which the criterion under discussion is applied to an idealized simple effective aircraft. The same effective aircraft example is used for each criteria discussed, thereby providing a basis for comparisons.
Essentially all of the reviews specifically address Category I PIOs, as there are no general criteria for Category II and III APC events. However, some analytical procedures for Categories II and III do exist, and some recent developments that show promise for predicting Category II conditions primarily associated with rate limiting are described at the end of this chapter.
Prerequisites For Criteria
A useful criterion must satisfy three prerequisites: validity, selectivity, and ready applicability.
Validity
"Validity" implies that a criterion embodies properties and characteristics that define the environment of interest and are associated with parameter spaces covering the vast majority of known cases. Because the PVS is a central component in severe PIOs, the criterion must relate to closed-loop, high-gain, aggressive, urgent, and precise piloted-control behavior. The connection can be either explicit or implicit; but it must derive from and reflect, in some sense, the fundamental principle that pilot actions combine with aircraft actions to result in a PIO. At a subtler level, it must be kept in mind that these combinations seldom occur, so the criterion should also emphasize the rarity of the events.
A logical assumption is that effective aircraft dynamics are designed to provide good flying qualities during normal flight maneuvers and tasks. The term good flying qualities includes very small, high-frequency effective time lags that do not require pilot compensation under normal circumstances and other features that are directly associated with exceptional pilot-aircraft properties in high-gain tracking-like situations. To be valid, the parameters in a criterion should somehow reflect these features.
The rarity of severe PIOs may also reflect the rarity of triggering events (i.e., out-of-the-norm, system-forcing functions or disturbances). Thus, a criterion that may guard against PIOs during normal maneuvers and small inputs may be useful even if it does not focus on flying qualities cliffs under extreme or unusual circumstances. Such a criterion would be valid for Category I events but could not rule out Category II or III tendencies.
The most useful criteria, of course, will give more information than simple pass/fail results. They will also provide additional information, such as relevance to specific PIO categories, conditions of validity (hence giving some hints about situations of unassessed risk), and frequency and bounding amplitudes of oscillation (which may indicate potential severity). Simple pass/fail results for a set of definable, likely circumstances are useful starting points. As a minimum, a "fail" can be a warning, and a "pass" can provide clearance with respect to a restricted group of APC possibilities. An explicit reference to the circumstances of a pass/fail result may indicate some of the more detailed, descriptive features that should be further examined by applying the analysis and simulation procedures described in Chapter 5.
Selectivity
"Selectivity" demands that the criterion differentiate sharply between "good" and "bad" systems. Criteria that downgrade the performance of aircraft that are actually adequate may be too restrictive. But there should be a clear differentiation at the level of acceptability. In the context of PIO prediction, the most important selectivity feature is the capability of distinguishing configurations that may be susceptible to severe PIOs from those that are not.
Ready Applicability
"Ready applicability" requires that the criterion be easily and conveniently applied. Expression of the criterion in terms of readily available system parameters should be compact. Procedures for analytical evaluations using the criterion should be convenient. The criterion measures should be easily determined using analytical models and/or empirical methods involving simulations or the actual aircraft and its systems.
Prominent Assessment Criteria For Category I
The most prominent criteria or partial criteria that have been proposed for assessing attitude-dominant Category I PIOs are the following:
- Aircraft-Bandwidth/Phase Delay, ωBW and τp48,49
- Gain/Phase Template, including ω180/Average Phase Rate8,22,24
- Smith-Geddes Attitude-Dominant Type III64,66
- Neal-Smith (original version,53 updated version,70 Moscow Aviation Institute version18)
- Dropback21,22
The theoretical bases for these criteria can all be related to a closed-loop PVS. Smith-Geddes Type III and Neal-Smith are explicitly based on pilot models related to compensatory control. The others are more implicitly connected with closed-loop piloting activities. The Aircraft-Bandwidth/Phase Delay and ω180/Average Phase Rate boundary constructions occupy a middle ground in that they reflect effective aircraft properties that affect high-gain, closed-loop control. Dropback measures are, strictly speaking, open-loop transient response properties of the aircraft, so their connection with closed-loop operations is the most obscure of this set of criteria. Nevertheless, a subtle connection does exist.
The Gain/Phase Templates, including ω180/Average Phase Rate boundaries, consider the effective aircraft attitude dynamics as an element of an open-loop system exhibited as coordinates on a gain/phase chart. (This and the other criteria forms are illustrated below in connection with their short reviews.) These open-loop effective aircraft characteristics can be explicitly associated with closed-loop PVS operations in which the pilot's behavior is synchronous (pure gain). The Aircraft-Bandwidth/Phase Delay measures are vehicle properties chosen to reflect key aspects of vehicle dynamics that affect the ease of pilot control and the tolerance for pilot dynamic variations in the crossover frequency region of the PVS during high-gain, precision-control activities.
The various parameters or metrics in all these criteria are typically used as coordinates to define parameter spaces. Boundaries in terms of these parameters are established to encompass pilot-rating data appropriate to given flying qualities levels or other concerns based on pilot ratings. Because pilot ratings are sensitive measures of the dynamics a pilot must exhibit to exert appropriate control in closed-loop tasks, the ratings intrinsically reflect both pilot and vehicle dynamics. The actual boundary lines for a given parameter, such as oscillatory APC potential or flying qualities levels, can then be drawn to reflect the desired qualities.
In principle, the boundaries could be different for different closed-loop task scenarios (e.g., precision tracking and tight regulation, closed-loop maneuvers, and large-amplitude corrective maneuvers) and for different types of pilot behavior. The boundaries for rotorcraft are a case in point.68 For fixed-wing aircraft, the boundaries for Neal-Smith, Aircraft-Bandwidth/Phase Delay, Gain/Phase Template, ω180/Average Phase Rate, and Dropback criteria have traditionally been drawn to distinguish between flying qualities Levels 1, 2, and 3. Only recently has considerable attention been given to boundaries peculiarly sensitive to PIO potential.
The following summary is provided for readers who are not concerned with the details and rationale for individual criteria. When viewed from an appropriate perspective, all the PIO assessment criteria for Category I PIOs listed above can provide insights and data that are useful in understanding PIO situations and their likelihood. At the moment, no one criterion meets all three prerequisites for criteria or delivers all the desired information—that is, none provides a comprehensive pass/fail estimate in terms of the frequency and circumstances of PIO occurrence. (PIO amplitude must be added for Category II and III situations.)
Each of the five criteria listed above is described below, followed by a discussion of extending these criteria to the lateral axis. In addition, a discussion on estimating the frequency of Category I oscillatory APC events is interposed between the discussions of the Smith-Geddes and Neal-Smith criteria.

Figure 6-1 Definitions of aircraft pitch attitude bandwidth and phase delay.
Source: Adapted from Mitchell et al.49
Aircraft-Bandwidth/Phase Delay
Aircraft-Bandwidth and Phase Delay are popular and effective criteria measures that have been successfully used to evaluate flying qualities.48,49 As illustrated in Figure 6-1, these are frequency-domain metrics that focus on particular characteristics of the aircraft attitude transfer function. The aircraft-attitude bandwidth, wBW, is a measure of the range of frequencies over which a pilot can exert good closed-loop control without having to compensate excessively (e.g., through the development of phase lead or the anticipation
needed to offset the time lags in effective aircraft dynamics). The aircraft-attitude bandwidth is also a measure of the range of frequencies within which the aircraft dynamics can accommodate changes in pilot gain that are necessary to execute both moderately and highly demanding tasks.
The phase delay, τp, limits the attainable closed-loop PVS bandwidth and governs the sensitivity to pilot gain of the PVS closed-loop resonance characteristics when the PVS is operating at the highest gains. The term "phase delay" is sometimes confusing because its dimensions are in seconds, but it is also an indication of the initial time delay in a response to pilot step inputs. Thus it is, at least partly, a time-domain measure.
Because these metrics are intimately related to closed-loop pilot-vehicle control and because they support a parameter space that covers almost all known cases, they satisfy the validity criterion.48 That is, within the frequency band defined by appropriate values of the aircraft bandwidth and phase delay, the effective aircraft dynamics tolerate either high or low pilot-gain and demand very little lead or other pilot compensation. They also satisfy the ready-applicability criterion in that they are ordinarily easy to extrapolate from analyses, simulations, flight test data, etc.
A useful indication of PVS sensitivity to gain changes near instability, when viewed in gain/phase coordinates, is the slope of the gain-phase curve in that region. Gibson24 defines Average Phase Rate as follows:

This slope is usually expressed in degrees/Hz.
A comparison with Figure 6-1 shows that the average phase rate and the phase delay are directly related. In general, the average phase rate is 720 τp degrees/Hz. Because the average phase rate is a direct multiple of the phase delay, it can be treated here along with the phase delay. It is a primary PIO indicator in the Gain/Phase Template, including ω180/Average Phase Rate criterion, which will be discussed next.
For single-loop PVSs, an idealized controlled element transfer function is Yc = Kc/s. Here, Yc is the transfer function that operates on the pilot's output to produce the system response, Kc is the controlled element gain, and the 1/s indicates an integration. As an idealization of longitudinal or lateral axis dynamics, this rate-control transfer characteristic results in constant-velocity pitching or rolling responses to pilot-imposed step-function command inputs to the elevators or ailerons. This characteristic also results in steady-state changes in pitch or bank angle in response to pulse inputs from the inceptors. For nonpilots, the characteristic can be envisioned as the idealized directional dynamics of a car when the turn rate is directly proportional to the deflection of the steering wheel.
These time-response attributes are the open-loop, effective aircraft properties. They are favorable for closed-loop piloted control because the pilot can close the loop acting in a pure-gain fashion in which pilot output is proportional to perceived error. There is thus no need for the pilot to generate any lead (anticipation) or lag compensation to close the loop. Furthermore, these idealized vehicle dynamics permit a very large range of pilot-gain adjustments. By simply increasing or decreasing gain, the pilot can establish a very wide range of closed-loop PVS bandwidths for the desired level of control precision without compromising the stability of the closed-loop system.
In terms of the open-loop PVS, gain changes directly change the open-loop crossover frequency. In the frequency domain, this ideal aircraft has an infinite aircraft-bandwidth, ωBW, and zero phase delay. Features such as the PVS open-loop crossover frequency, precision of control, and disturbance suppression are totally controlled by the gain adopted by the pilot. With these idealized effective aircraft dynamics, the pilot's lags become the limiting factor in closed-loop operations. The closed-loop neutral stability frequency for this PVS, when pilot lags are taken into account, is 0.84 Hz (5.25 rad/sec); this frequency can be considered to be at or near the upper limit for closed-loop compensatory control.42
Well-designed aircraft and FCSs can produce attitude characteristics in the effective aircraft dynamics that approximate the ideal Kc/s form in the region of PVS crossover, thereby requiring very little pilot lead and permitting large variations in pilot gain. The higher-frequency effective aircraft dynamics, however, contribute a variety of lags and leads that alter the (stability-constrained) available crossover region both quantitatively and qualitatively. These higher frequency dynamics have a first-order effect on the aircraft-attitude bandwidth, ωBW, which for ''good" aircraft can be measured by the frequency at which ![]() Yc = −135 degrees. This corresponds to a pure-gain pilot loop-closure with a phase margin of 45 degrees (i.e., 180 degrees minus 135 degrees). A phase margin of zero corresponds to a PIO of the PVS. The change in closed-loop system resonance (i.e., peak magnification ratio*) as a result of a change in pilot gain is governed by how fast the phase is changing at frequencies somewhat higher than the aircraft bandwidth frequency. Thus, a phase that changes slowly at frequencies above ωBW permits a larger, smoother, and better graded increase in pilot gain without undue changes in the closed-loop system characteristics than is possible with a more rapidly changing phase. The pilot is confronted with a less drastic change in closed-loop system properties when operating near the maximum gain levels.
Yc = −135 degrees. This corresponds to a pure-gain pilot loop-closure with a phase margin of 45 degrees (i.e., 180 degrees minus 135 degrees). A phase margin of zero corresponds to a PIO of the PVS. The change in closed-loop system resonance (i.e., peak magnification ratio*) as a result of a change in pilot gain is governed by how fast the phase is changing at frequencies somewhat higher than the aircraft bandwidth frequency. Thus, a phase that changes slowly at frequencies above ωBW permits a larger, smoother, and better graded increase in pilot gain without undue changes in the closed-loop system characteristics than is possible with a more rapidly changing phase. The pilot is confronted with a less drastic change in closed-loop system properties when operating near the maximum gain levels.
At the limits of control encountered with high pilot gains, where the phase effects are significant, the aircraft bandwidth alone is not a sufficient measure. The phase delay (τp) accounts for these higher-frequency features.49 As a closed-loop system metric, the phase delay emphasizes the aircraft contribution to the phase changes in the region of the unstable frequency for

Figure 6-2 Aircraft-Bandwidth/Phase Delay/Dropback requirements for PIO resistance in terminal flight phases. Source: Klyde.39
the effective PVS. When the pilot is operating in a pure gain (i.e., synchronous) mode, this is the total system phase change. Therefore, it should be particularly sensitive to synchronous-pilot Category I PIOs, although it is not confined to this variety.
The particular boundaries in the Airplane Bandwidth/Phase Delay space can be drawn to include or exclude data points in the experimental pilot ratings and other PVS data. Thus, when boundaries connected with flying qualities levels are appropriate, the critical data sets may include high-gain tracking tasks (where the compensatory control and pursuit modes of pilot behavior are important), as well as precision maneuvers (where combined open-loop and closed-loop pilot operations are important, i.e., where pursuit and precognitive control modes may be major discriminators).
For PIOs, data sets appropriate for either or both compensatory and synchronous high-pilot-gain operations are relevant. PIO-specific boundaries would incorporate Level 1 flying qualities boundaries as a subset because a PIO-prone aircraft can never be considered to have Level 1 flying qualities. (Level 1 flying qualities are defined as "clearly adequate for the mission…aircraft is satisfactory without improvement."20)
Bandwidth and phase delay boundaries pertinent to predicting PIOs that take into account data from research aircraft have been used to examine in detail the application of bandwidth and phase delay concepts to Category I PIO assessment. These boundaries are, of course, tuned and refined as the data base expands. The boundaries shown in Figure 6-2 are the best and most current. Aircraft-Bandwidth/Phase Delay criteria boundaries are "most effective at correlating PIO tendency ratings for pitch tracking and landing."70 The region not susceptible to PIO is the rectangle defined by 1 ≤ ωBW ≤ 6 rad/sec and 0 ≤ τp ≤ 0.15. Other considerations, such as dropback, can be used to expand the PIO-prone space on an ad hoc basis.48

Figure 6-3 Aircraft-Bandwidth/Phase Delay parameters as indicators of PIO susceptibility for sample operational and test aircraft. Source: Adapted from Klyde.39
In Figure 6-3, a variety of operational and test aircraft are plotted against these basic boundaries. The results show that the boundaries are generally very good for distinguishing between severe PIOs of the Have PIO configurations and their non-PIO baseline conditions (i.e., Have PIO configurations 2-1, 3-1, and 5-1).5 (Have PIO refers to a series of experiments that collected important PIO data during flight experiments with aircraft in various configurations. Indeed, these data had much to do with establishing the boundaries). The ALT-5 case is shown as PIO prone, although it is close to the upper boundary of non-PIO prone configurations. The F-8 DFBW PIO case can be traced through various sequences from CAS + 100 ms to Direct + 100 ms to Direct to SAS. The highest quality and most complete data enclosed by the boundaries are consistent with pilot operations in a compensatory context, so the boundaries are certainly pertinent for these situations. Synchronous-pilot data points may also be included.
The very limited Category II and III situations (e.g., PIOs for aircraft such as YF-12 and X-15) are generally not well covered by the Aircraft-Bandwidth/Phase Delay boundaries per se. The linear manifestations of these tendencies occur well within the "not susceptible" region. The addition of an
"excessive dropback" region permits the inclusion of the T-38 PIO, during which the pilot behavior was almost surely synchronous.
One problem with the application of Aircraft-Bandwidth/Phase Delay criteria is the definition of the input to the effective aircraft. As currently defined, input is inceptor force (although for much of the data underlying the criterion, position could be used just as well).48 Thus, lags and nonlinearities in the artificial feel system are explicitly included in measurements of attitude/control input transfer characteristics. On FBW aircraft, the nature of the pilot's inceptor can be more varied than on conventional aircraft, ranging from force sticks to driven columns with proprioceptive display features, such as force changes feeding back various pieces of information. The pilot's limb-neuromuscular system (i.e., the pilot's "actuation elements") can accommodate a wide variety of feel-system nonlinear characteristics.27 Consequently, it may not be reasonable to confine the form of pilot input.
In applying the Aircraft-Bandwidth/Phase Delay and other frequency domain criteria to the Boeing 777, a distinct preference was developed for inceptor position because "position-based data yield more consistent and coherent frequency response results and reduce uncertainty in determination of phase delay and bandwidth.54 Boeing also found that using position inputs simplified comparisons of feel-system frequency responses for all their aircraft.
In general, the data base on transport aircraft in terms of Aircraft-Bandwidth/Phase Delay and Average Phase Rate is small. It has been significantly expanded during the course of this study by Boeing's release of flight data for several aircraft.54 These data demonstrate that the 747, 757, 767-300ER, and the 777 (in "normal," "secondary," and ''direct" FCS modes) have phase delay values of less than 0.14 sec when column position is used as the input. The aircraft attitude bandwidth values also fall within the Figure 6-3 boundaries. Specific examples for the 777 based on in-flight measurements are included in Figure 6-3. Another example is shown for the MD-11 using estimates with τpθ values based on column deflection rather than column force. Thus the boundaries of Figure 6-3 for attitude-dominant PIOs, which were originally based primarily on data from fighter and research aircraft, appear to be applicable to transport aircraft as long as input is appropriately identified.
The Aircraft-Bandwidth/Phase Delay indicators do not explicitly estimate likely PIO frequency. However, the synchronous-pilot (Yp = Kp) PVS neutral stability frequency (ωu = ω180) is used in the calculation of the phase delay, although this frequency is not always called out as part of the PIO assessment information. When it is called out, and to the extent that PIOs are associated with open-loop pilot characteristics that approximate a pure gain at the PIO frequency, ω180 is an estimate for ωPIO. But, to the extent that the PIO is a phenomenon of a compensatory PVS, ω180 can be an incorrect estimate. It is important to note that this discussion of PIO frequency estimates does not
imply that the suggested Aircraft-Bandwidth/Phase Delay boundaries for PIO shown in Figures 6-2 and 6-3 assume synchronous-pilot control behavior.
For most extended-rigid-body effective aircraft dynamics, where the higher frequency flexible modes do not significantly affect the phase or amplitude ratio* plots at frequencies below or near 2 ω180, the bandwidth and phase delay measurements are usually straightforward. These measures could be more ambiguous in situations of roll-attitude control if lateral-directional coupling effects are prominent near ωBW, ω180, or 2 ω180. Uncertainties and ambiguities also appear in the presence of flexible-body modes, as in the case of the YF-12.
Illustrative Example
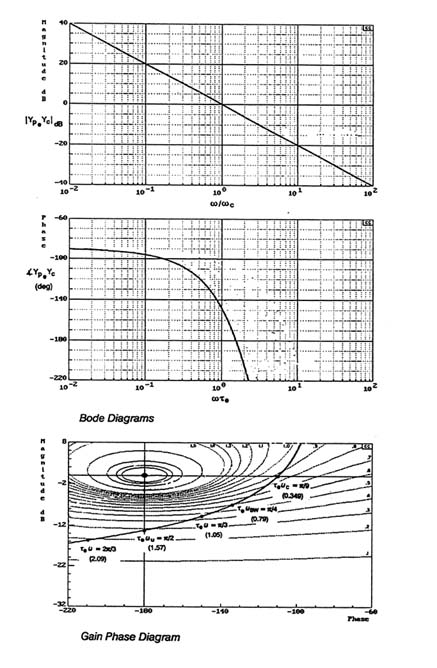
To illustrate the use of Aircraft-Bandwidth/Phase Delay and Average Phase Rate for predicting severe APC events, consider that the controlled element attitude dynamics can be approximated in the region of the PVS crossover frequency by the transfer function:

This simple, idealized form is an appropriate first-order approximation of the attitude properties in the crossover frequency region for well designed effective aircraft dynamics. It is worth emphasizing again that this elementary form is intended to approximate a restricted range of frequencies and that the effective time delay (τe) is a composite low-frequency approximation to a potentially large number of lead and lag time constants and pure time delays that may occur well above the crossover frequency region.
The open-loop Bode diagrams* (i.e., gain and phase versus frequency) and gain/phase diagrams for this system are shown in Figure 6-4. On the gain/phase plot, the gain (Kc) is arbitrarily set so that the crossover frequency (where the amplitude ratio is 1.0 or 0 dB) occurs when the phase is −110 degrees, to be consistent with the convention adopted by Buchacker, et al., for gain/phase templates.8 The aircraft bandwidth (ωBW) and the instability frequency (ωu = ω180) for a pure-gain closure are identified on the figure. For this system, the quantities are given by ωBW = π/4τe rad/sec [fBW = 1/8τ e Hz], and ωu = π/2τe [fu = 1/4τe Hz]. The phase delay for this effective controlled element is τp = τe/2. The average phase rate ɸωu) is a direct multiple of the phase delay (by 720 degree/Hz), so it will be 320 τe degree/Hz.
Table 6-1 shows aircraft bandwidth, phase delay, and average phase rate characteristics for a sequence of τe values for this idealized rate-command-controlled element. It also shows the neutral stability frequency when the system is closed by a synchronous pilot.
TABLE 6-1 Idealized Rate-Command Controlled Element Characteristics
|
τe (sec) |
|
|
ωu (rad/sec) |
f180 (Hz) |
|
(deg/Hz) |
|
0.10 |
7.85 |
0.05 |
15.7 |
2.5 |
5.73 |
36 |
|
0.15 |
5.24 |
0.075 |
10.5 |
1.67 |
8.60 |
54 |
|
0.20 |
3.93 |
0.10 |
7.85 |
1.25 |
11.46 |
72 |
|
0.25 |
3.14 |
0.125 |
6.28 |
1.0 |
14.32 |
90 |
|
|
||||||
|
0.30 |
2.62 |
0.15 |
5.23 |
0.83 |
17.19 |
108 |
|
0.35 |
2.24 |
0.175 |
4.49 |
0.71 |
20.06 |
126 |
|
|
|
|||||
|
0.40 |
1.96 |
0.20 |
3.92 |
0.62 |
22.92 |
144 |
|
0.45 |
1.75 |
0.225 |
3.49 |
0.55 |
25.78 |
162 |
|
0.50 |
1.57 |
0.25 |
3.14 |
0.50 |
28.65 |
180 |
|
Source: McRuer.42 |
||||||
The Aircraft-Bandwidth/Phase Delay boundaries in Figure 6-2 suggest that an aircraft will be susceptible to PIOs if τp![]() 0.15 sec for Flight Phase Categories B and C.48 (Note that these categories refer to flight phases rather than to PIO categories. Flight Phase Categories are part of the flying qualities esoterica—Flight Phase Category C, for instance, refers to terminal flight phases including approach and landing.) Thus, statements in the study by Mitchell, et al., are compatible for Flight Phase Categories B and C. For Flight Phase Category A (nonterminal flight phases that require rapid maneuvering, precision tracking, or precise flight-path control), τp> 0.19 is unfavorable from a PIO standpoint.48 In terms of the Table 6-1 cases, these criteria would imply that idealized rate-command effective vehicle characteristics with effective time delay parameters greater than 0.38 sec for Category A flight or 0.30 sec for Categories B and C are likely to be prone to PIO.
0.15 sec for Flight Phase Categories B and C.48 (Note that these categories refer to flight phases rather than to PIO categories. Flight Phase Categories are part of the flying qualities esoterica—Flight Phase Category C, for instance, refers to terminal flight phases including approach and landing.) Thus, statements in the study by Mitchell, et al., are compatible for Flight Phase Categories B and C. For Flight Phase Category A (nonterminal flight phases that require rapid maneuvering, precision tracking, or precise flight-path control), τp> 0.19 is unfavorable from a PIO standpoint.48 In terms of the Table 6-1 cases, these criteria would imply that idealized rate-command effective vehicle characteristics with effective time delay parameters greater than 0.38 sec for Category A flight or 0.30 sec for Categories B and C are likely to be prone to PIO.
This example will be used again to illustrate other candidate criteria.
Gain/Phase Template (including ω180/Average Phase Rate) Criteria
The Gain/Phase Template (including ω180/Average Phase Rate Criteria) has some of the same features as the Aircraft-Bandwidth/Phase Delay criteria, with an additional element for the gain of the effective aircraft dynamics.24 The criteria are shown in Figure 6-5. The boundaries, which are defined in terms
of the frequency at 180-degree phase lag of the pitch attitude frequency response, ω180, and the average phase rate, are similar in form to the Aircraft-Bandwidth/Phase Delay plot of Figure 6-3, except for the details. If synchronous-pilot activity is assumed, this formulation directly indicates the PIO frequency region.
The boundaries in Figure 6-5 were originally intended to indicate flying qualities in general rather than PIOs in particular. A comparison of Figures 6-3 and 6-5 shows that flight data (such as Have PIO 2-8) fall along the L2-L3 boundary.5 This boundary is currently used as a dividing line for assessing PIO potential. In drawing this boundary, Gibson intended that it discriminate, among other things, between PIO-prone and non-PIO cases with which he was familiar. It does accomplish this for much of the data shown in Figure 6-3. Like other proposed boundaries, however, this one is subject to adjustment and fine tuning as more data become available.
Note that the average phase rate associated with PIO-prone conditions would correspond to a phase delay of 0.20 sec. This is 0.05 sec larger than the phase delay in Figure 6-3 but very close to the 0.19 sec suggested for Flight Phase Category A. Thus, in Table 6-1, the PIO potential dividing line based on the average phase rate from Figure 6-5 is at a lower level for the idealized rate-command controlled element than the dividing line based on Figure 6-3.
A notable difference between the Gain/Phase Template and other criteria reviewed here is the attempt to quantify the gain of the effective aircraft dynamics. This is shown in the amplitude boundaries portion of Figure 6-5. The boundaries are based on center stick inceptors as the cockpit longitudinal control devices. Analogous values for other inceptors have not yet been established.
Smith-Geddes Attitude-Dominant Type III Criterion
The application of the Smith-Geddes criterion for attitude-dominant PIOs has been developed and described.64,66 As the basis for this criterion, Smith developed a very simple linear formula for the crossover frequency from an early (circa 1965) series of extensive, fixed-base experiments on a cross section of elementary systems. The formula is

where m is an "average slope" in dB/octave of the effective aircraft dynamics in the crossover region.64 This formula does not explicitly depend on the phase rate It provides an estimate of the crossover frequency for a compensatory PVS based on controlled element dynamics other than the dynamics on which the equation is based.
The elementary system dynamics (Yc = Kc, Kc /s, and Kc /s2) used to develop the empirical data base had no higher-frequency net lags. The pilot's inceptor was a spring-restrained side stick with no other dynamics, and all measurements were based on stick position (although the spring restraint was linear, so the pilot's output force is proportional to the stick deflection). Therefore, this crossover frequency is appropriate to the crossover model for conditions where high-frequency lags and leads beyond the crossover region are not included; aircraft lags within the crossover region are implicitly included.45(In this context, the crossover region, would extend from about 1 to 8 rad/sec [0.16 to 1.27 Hz].) When the lags associated with more complex effective aircraft dynamics are included, the nominally positive phase margins associated with the elementary system types on which the formula is based may be assumed if the same crossover characteristics are maintained.
The Smith-Geddes Type III criterion for attitude-dominant PIOs is a straightforward test of whether or not a positive phase margin exists when the actual effective aircraft dynamics are examined at the crossover frequency. That is, an attitude-dominant, compensatory system, single-loop PIO is predicted if the following condition is met:

Although this criterion explicitly involves only the effective aircraft dynamics, θ/Fes, relating the pitch attitude to the stick force, the pilot characteristics have been accounted for via the definition of the crossover frequency, which is also referred to as the criterion frequency.
As a PIO predictor, the Smith-Geddes Type III criterion works well for Category I severe PIOs (which are essentially linear) from the Have PIO data.5 The criterion is selective between "good" baselines and severe PIO subsets. It has accurately predicted that a variety of aircraft were prone to PIO.64 The criterion was also effective in showing PIO tendencies for configurations in the data base compiled by Neal and Smith (1970).53
The ωc column in Table 6-2 is based on the Smith-Geddes Type III formula, while ωPIO and ɸ(θ/Fes) are measured data for the operational and test aircraft documented in the study by Klyde et al.,39 and the severe PIOs from the Have PIO data base.5 The PIO Prone column is based on the Smith-Geddes Type III criterion. As shown in Table 6-2, the Shuttle ALT-5, F-8 DFBW, and Have PIO data are well covered by the Smith-Geddes criterion.
The Smith-Geddes Type III criterion has been proposed for addition to the MIL-STD-1797A along with features of the Gain/Phase Template.70 The review of research aircraft data gathered after the original development of handling quality requirements for the design of the fighter aircraft48,66 indicates that the Smith-Geddes criterion can be very conservative; that is, it may predict that more configurations are susceptible to PIOs than actually are.
TABLE 6-2 Prediction of PIO Susceptibility with Smith-Geddes Attitude-Dominant Type III Criterion for Operational and Test Aircraft
|
Aircraft |
ωPIO (rad/sec) |
ωc (rad/sec) |
ɸ(θFes) (deg) |
Type III PIO Prone |
|
Have PIO 2-1 (baseline) |
no PIO |
4.37 |
-161.0 |
no |
|
Have PIO 2-5 |
2.7 |
3.18 |
-211.6 |
yes |
|
Have PIO 2-8 |
3.8 |
4.33 |
-201.5 |
yes |
|
Have PIO 3-1 (baseline) |
no PIO |
5.06 |
-127.9 |
no |
|
Have PIO 3-12 |
2.2 |
3.26 |
-225.6 |
yes |
|
Have PIO 3-13 |
3.2 |
3.97 |
-223.9 |
yes |
|
Have PIO 5-1 (baseline) |
no PIO |
3.77 |
-167.6 |
no |
|
Have PIO 5-9 |
3.5 |
3.56 |
-216.9 |
yes |
|
Have PIO 5-10 |
2.7 |
3.14 |
-229.5 |
yes |
|
X-15 Flight 1-1-5 |
3.3 |
4.14 |
-170.9 |
no |
|
T-38 Bobweight Closed |
7.8 |
5.52 |
-66.0 |
no |
|
T-38 Bobweight Open |
7.8 |
5.45 |
-108.4 |
no |
|
YF-12 Rigid Body Only |
3.5 |
4.97 |
-142.6 |
no |
|
Shuttle ALT-5 |
3.4 |
3.84 |
-193.1 |
yes |
|
F-8 DFBW CAS + 100 msec |
3.1 |
4.10 |
-215.2 |
yes |
|
F-8 DFBW Direct + 100 msec |
3.1 |
3.65 |
-232.5 |
yes |
|
F-8 DFBW Direct |
3.1 |
3.65 |
-211.6 |
yes |
|
F-8 DFBW SAS |
3.1 |
4.15 |
-179.8 |
borderline |
|
B-2 Off-Nominal Approach |
2.7 |
3.21 |
-210.0 |
yes |
|
B-2 Aerial Refueling |
3.8 |
5.05 |
-158.0 |
no |
|
Source: Klyde.39 |
||||
Of the 51 cases examined by Mitchell et al,48 the Smith-Geddes criterion predicted that 48 should be susceptible to PIO, but only 17 actually exhibited PIOs. All configurations with a PIOR of 3 or greater were in the latter group, whereas many of the configurations with PIORs of 1 did not exhibit PIO tendencies.
The Smith-Geddes Type III criterion was used to evaluate a variety of Boeing aircraft (757-200, 767-300ER, 747-400, and 777). All passed the criterion, although several were marginal (6 data points out of 15 had phase angles ranging from –164 to –180 degrees at the criterion frequency; only 1 point was from a 777)54 The frequency response data was based on column position as an input. The 6 data points of highest quality in this set were for the 777 (in "normal," "secondary," and "direct" FCS modes) engaged in very high gain, simulated, aerial refueling tasks. It received a CH PR of 2 and a PIOR of 1 to 2 from both evaluating pilots.
Illustrative Example
When the Smith-Geddes criterion is applied to the elementary example of an idealized rate-command effective aircraft (i.e., Yc = Kce-jωie /jω), the criterion frequency (ωc) is,

The effective time delay (ιe) corresponding to a predicted PIO condition is

This corresponds to a phase delay (τp) of 0.172 sec and an average phase rate of 124 deg/Hz. These values are close to the analogous values under the Aircraft-Bandwidth/Phase Delay and Gain/Phase Template, including ω180/Average Phase Rate criteria. The effective time delay is less than the 0.20 sec from the Average Phase Delay criterion and lies midway between the estimates of 0.15 and 0.19 sec from the Aircraft-Bandwidth/Phase Delay boundaries for Flight Phase Category A and Flight Phase Categories B and C.
Comparison of assessments for PIO potential using Gain/Phase Templates, Aircraft-Bandwidth/Phase Delay Criteria, and the Smith-Geddes Type III criterion for this example is somewhat confusing. That is, in this instance Smith-Geddes appears to occupy a middle ground and is not overly conservative. Taking everything into account, one could conclude that meeting the Smith-Geddes Type III criterion indicates a very low probability of an attitude-dominant PIO, although failing it does not necessarily mean that a PIO will occur.
An important aspect of PIO assessment is the estimate of the likely PIO frequency. Using the Smith-Geddes Type III criterion, the criterion frequency of Equation 6-3 is the estimated crossover frequency of the pilot-aircraft open-loop system and also the PIO frequency. The consequences of this can be tested with the Have PIO,5 which are recapitulated as part of Table 6-2. A linear regression for the six severe PIO cases gives
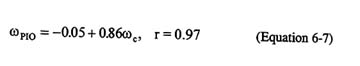
The regression is shown in Figure 6-6, which also contains the other data from Table 6-2. In general, Figure 6-6 demonstrates that the estimate of the
frequency of Category I PIOs using the existing formula for ωc is higher than has actually been observed. This implies that the effects of higher frequency lags are underestimated in the Smith-Geddes determination of the criterion frequency. This is surely one reason for the lack of selectivity of the criterion as it is currently constituted.
Equation 6-3 gives a high value for ωc for a variety of underlying reasons. They include the very high performance levels of the subjects for the experiments (which were conducted 30 years ago) and the very linear, no-lag, side-stick-like inceptor that was used. Equation 6-3 could probably be refined to be more selective using the much more extensive data now available.45 These data would give less conservative results and could also be adjusted to account for specific inceptor types and experimental scenarios, such as fixed-base, moving-base, or in-flight simulations.
The fundamental Bode relationships between amplitude ratio and phase show that all the minimum-phase properties of a transfer function can be accounted for by defining either the amplitude-ratio or the phase over all frequencies. By including a term involving the amplitude ratio slope in the Equation 6-3 formula for the crossover frequency, the phase lags that have amplitude-ratio effects in the region of the slope measurement are taken into (very) approximate account. But any higher frequency lags from dynamics well above the crossover frequency appear as non-minimum-phase contributions in the frequency range covered by Equation 6-3 and are not reflected in local measurements of the amplitude-ratio slope. There were no such lags in the empirical data on which Equation 6-3 was based. Consequently, adjusting the equation to take into account the higher frequency contributions may be appropriate. The effect would be to reduce the criterion frequency and make the Smith-Geddes Type III estimate of PIO tendencies less conservative.
An important feature of the ready applicability of a criterion is the manner in which the amplitude-ratio slope (m) is computed. Fitting a frequency-response amplitude ratio with a straight line in the crossover region is seldom as unambiguous as it is in the idealized rate control system in the illustrative example. For example, an evaluation of a B-2 susceptibility to PIOs provides a realistic case showing that the Smith-Geddes criterion does not account for PIOs experienced by the B-2 unless the details of the slope computation are modified.26
Estimating the Frequency of Category I Oscillatory APC Events
The potential PIO frequency is very important for several reasons. First, it reflects the system characteristics that underlie the oscillation, and second, it
points to changes that might be made to reduce the PIO tendency. It also indicates the most sensitive frequency regions of the closed-loop PVS, provides a basis for selecting test inputs, and is useful in several other ways. In all the cases and criteria treated here, PVS dynamics are extended-rigid-body characteristics and only the lower-frequency effects of higher-frequency modes are considered. In these situations, PIO frequency is always less than 1 Hz (3.14 rad/sec) when the pilot is operating in a compensatory manner, and it may be as high as, perhaps, 2.5 Hz (8 rad/sec) for fully-developed synchronous operations.
Alternative methods for estimating the frequency of Category I PIOs abound. The Smith-Geddes formula (Equation 6-3) comes close when the high frequency time lags are small. When time lags are larger, the estimate of PIO

Figure 6-6 Correlation between Smith-Geddes criterion frequency and Have PIO flight data.
Source: Klyde.39
frequency using the Smith-Geddes estimate for wc can be improved by using Equation 6-7. This approach is suggested not only by its successful fit to the Have PIO data but also by the (possible) coincidence that it is not too far off for the other aircraft represented in Figure 6-6. Because Equation 6-7 is purely empirical, it could, perhaps, be refined using additional PIO data.
A better way to make estimates when the pilot is operating in a compensatory mode is to apply the pilot-modeling routines to find the neutral stability frequency from specific pilot-model estimates for particular effective aircraft dynamics.45 Although this method is more complicated than using Equation 6-3, it is straightforward and can also provide a good deal of information about pilot dynamic behavior, including pilot-adopted compensation, second-order effects of inceptors, and pseudo ratings and commentaries. In fact, this approach has so much to offer in terms of detailed understanding that the committee believes it should always be used in situations that exceed a threshold of concern. The potential accuracy of this procedure can be appreciated by using Bjorkman's estimates (based on a version of the general compensatory-pilot model) of the attitude-control resonant frequency (ωr) for the Have PIO data.5 The linear regression42 relating these estimates to the (later) observed PIO frequency data is:
The correlation between ωr and ωPIO is excellent, as is the correlation coefficient, r for this restrictive data set. It also suggest that the Have PIO Category I PIOs were fundamentally compensatory in nature.
The quickest and least-complicated procedure for estimating ωPIO using a pilot model that accounts for high frequency lags is to apply the crossover model to the Have PIO data with the result:
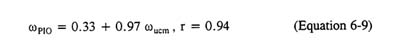
where ωucm is the neutral stability frequency [ ![]() Yp Yc (jωucm) =−180 degrees] as predicted by the crossover model. Thus, the elementary crossover model, combined with a rough first approximation of the effective time lag of the PVS, appears to capture enough of the underlying phenomena to provide a reasonable estimate of PIO frequency.
Yp Yc (jωucm) =−180 degrees] as predicted by the crossover model. Thus, the elementary crossover model, combined with a rough first approximation of the effective time lag of the PVS, appears to capture enough of the underlying phenomena to provide a reasonable estimate of PIO frequency.
Another easy way to make an estimate of PIO frequency is to connect ωPIO with the neutral stability frequency for the synchronous-pilot pitch-attitude control system. This is, of course, the ω180 frequency in the aircraft-bandwidth/phase delay definitions. McRuer42 gives this relationship for the severe PIO data as
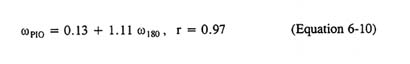
Thus, if this empirical equation can be generalized, the estimated PIO frequency is somewhat greater than 111 percent of the frequency predicted for a synchronous pilot interacting with the aircraft's attitude dynamics.
This result has some interesting implications. For example, the pilot, if, operating primarily on attitude cues, must be providing a phase advance at the PIO frequency that more than offsets all of the internal time lags. An alternative explanation could be that the dominant cues available to the pilot in the Have PIO flights include pitch rate or another aircraft output variable (e.g., sight line) that leads attitude oscillations, thereby compensating for pilot time lags. The Bjorkman data are insufficient to decide among such speculations, although some time traces from other PIO sources indicate that pilot switching on rate cues may occur in some cases.9,23
For the present, one can interpret equations 6-7 and 6-10, respectively, as statements that the Smith-Geddes ωc estimate is higher than the actual PIO frequency and that the ω180 neutral stability frequency for pure gain attitude control is lower than the actual PIO frequency. If these correlation's are shown to be generally correct, they could be useful, easily calculated bounds on Category I PIO frequencies. A useful rule of thumb might be to sum and average equations 6-7 and 6-10:
Equation 6-11 implies that an estimate for Category I ωPIO is not far from the mean of ω180 and the Smith-Geddes ωc. When using this experimental relation, the investigator should remember the ancient principle of caveat emptor.
Neal-Smith Criteria and Modifications
The Neal-Smith approach is solidly based on closed-loop operations. However, the normal Neal-Smith boundaries are connected with flying qualities levels rather than PIO potential per se. In this context, PIO-potential is one factor but not the factor that leads to a non-Level 1 aircraft. Thus, Neal-Smith, as presently constituted, is not selective for PIO. However, suitable modifications to the boundaries might enable a Neal-Smith approach be used a criterion for PIO susceptibility.
Some work on modifying Neal-Smith Criteria has already been done by the Moscow Aviation Institute.18 The Neal-Smith53 and LAHOS63 configurations were examined in piloted-simulator studies with tracking tasks, taking detailed measurements of pilot and pilot-vehicle dynamic characteristics as well as pilot CH PR and PIO rating. Neal-Smith-like boundaries were then developed using actual experimental data for the pilot lead (as a workload indicator) and a closed-loop PVS peak magnification ratio. Different
boundaries were drawn for flying qualities levels and for PIOs. The PIO boundaries are shown in Figure 6-7.
Illustrative Example
The Neal-Smith approach requires the analyst to estimate the open-loop pilot lead (or time lag) and the closed-loop system resonance using a particular pilot model. The rules for adjusting the pilot characteristics within the fixed-form model include constraints on the closed-loop system bandwidth and droop.53 These rules have been applied to the idealized rate-command aircraft for a succession of effective time delays (τe). As summarized in Figure 6-8, as the delay increases there is a demand for more pilot lead and an increase in closed-loop resonance. This trend shows how the pilot might cope with increasing controlled-element time lags to maintain control precision (as defined by the closed-loop bandwidth) at a desired level. This example also shows how the Moscow Aviation Institute PIO boundaries can be used in the context of the trend line. The intersection of the boundary and the trend line occurs at an effective time delay of approximately 0.29 sec. This corresponds to a phase delay of 0.145 sec or an average phase rate of 104 degrees/Hz. The remarkably close agreement with the previous illustrative examples gives credence to the view that Neal-Smith concepts can be expanded to examine PIO-susceptibility trends.
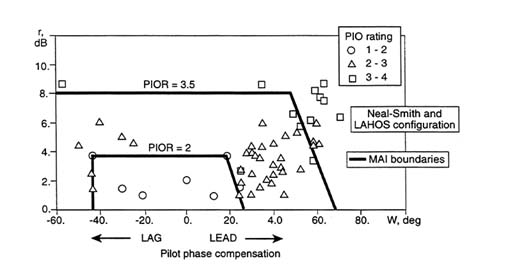
Figure 6-7 Moscow Aviation Institute PIO boundaries. Source: Efremov.18
Dropback
The Dropback parameter, Δθpeak, which is illustrated in Figure 6-9, deals with metrics, such as qpeak/qss, derived from the attitude response to step inputs. Dropback may not appear to be an accurate measure of closed-loop PVS response because, strictly speaking, it is an open-loop aircraft response. However, the Dropback characteristics Δθpeak and qpeak/qss for Kc/s vehicle dynamics are zero. Then, when the effective vehicle dynamics (Yc) become more complex and depart from a Kc/s-like character, they become larger. Dropback can thus be interpreted as a time-domain indicator of the degree of ''K/s-ness" exhibited by a particular set of effective aircraft attitude dynamics. One facet of PVS resistance to PIO is insensitivity to variations in pilot gain, in the case of the ideal rate-command controlled element, for example. To the extent that an ideal PIO-insensitive aircraft has dynamics approximating K/s over a suitably prescribed frequency regime, the Dropback parameter can be used a measure of this feature of PIO susceptibility.
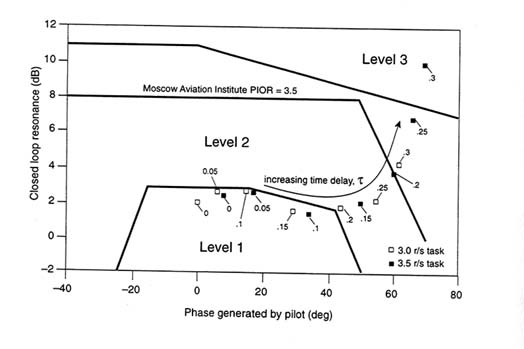
Figure 6-8 Neal-Smith trends with variation of effective delay for Kc e-sτ/s.
Because the pulse applied as the test input is really two pulses separated by 10 sec, Dropback is not sensitive to high-frequency effective delays. For instance, the Dropback for the rate-command controlled element with an effective time delay of Equation 6-2 is zero, just as it is for a pure Yc = Kc/s rate command transfer function. The Dropback parameters, by themselves, are therefore insufficient as a PIO criterion. However, the combination of Dropback parameters and the average phase rate do provide a useful PIO criterion. As has already been noted in connection with Figures 6-2 and 6-3, Dropback can occasionally be used to justify eliminating otherwise awkward data.
The Dropback criterion boundary shown in Figure 6-9 was based primarily on data from fighter aircraft. The data points shown on the figure (x1, x2, x3) are from flight tests of the Boeing 777 and correspond to the flight conditions added to Figure 6-3. They are shown here to justify the assertion that the Dropback parameter can also be applied fruitfully to FBW transport aircraft.
Because Dropback is a good measure of K/s character, it is applicable only to rate-type controlled elements; it will not apply directly to special controlled-element forms such as attitude command or flight-path command effective vehicle dynamics.
Extending Criteria to the Lateral Axis
The discussion so far has emphasized the dynamics of pilot control of the longitudinal axis. Some of the same metrics, criteria, and approaches have been examined for control of the lateral axis, although not to the same extent. Unfortunately, the research and detailed test and operational aircraft data bases for lateral-axis control are much more limited, and the effects of pilot-controller sensitivity are not as well accounted for. The most current and complete summary concludes that "PIO is unlikely if phase delay is less than 0.17 sec, as long as [controller] sensitivity is separately optimized; and PIO is likely always if phase delay is above about 0.17 sec."48 A comparable value of average phase rate would be 122 degrees/Hz.
Mitchell and Hoh48 also examined the Smith-Geddes criterion using the same experimental data on lateral-axis control. The Smith-Geddes criterion reliably predicted all but one of the PIO events. Unfortunately, a fair number of non-PIO susceptible systems were PIO-prone according to this criterion, once again indicating that the Smith-Geddes criterion may be overly conservative.
Two current reviews of assessment criteria have concluded that the lack of data on effective controlled element gain (i.e., cockpit-controller gain), especially for novel inceptors, is a major deficiency for assessing Category IPIOs.39,48 Even the best set of optimum aircraft dynamics can become PIO-prone
if the gain is too sensitive.42 In past experiments, this variable has been fairly well controlled to be near optimum levels for conventional cockpit longitudinal-control devices. This has not been true of lateral control devices.
In the thorough flight investigations of PIO susceptibility conducted during the development phases of the Boeing 777 aircraft, Aircraft-Bandwidth/Phase Delay and Smith-Geddes Type III measures were examined for both the lateral and longitudinal control axes. A flight test series involving simulated refueling and other high-gain pilot experiments received a CH PR of 2 and a PIO rating of 1 to 2. The phase delay was always less than 0.14 sec when wheel position was used as the input. When the input was wheel force, the phase delay values increased markedly, from a minimum of 0.2 sec to 0.34 sec.
The bank-attitude-to-wheel-position phase angle, evaluated at the frequency specified by the Smith-Geddes criterion, did not fare as well as the phase delay. Although the data were clustered around −180 degrees, thereby indicating a marginal PIO tendency based on the Smith-Geddes criterion, the pilot evaluations during extensive simulation of refueling and other high-gain closed-loop tasks showed no PIO tendencies whatsoever.
Ongoing research to improve criteria has contributed to more comprehensive specifications by the military (see below) and the FAA. Even so, currently there are no specific requirements to conduct APC-related testing of either military or commercial aircraft during the development and certification process; specific procedures that address APC concerns are generally at the discretion of the manufacturer.
Military Status And Trends
Development of New Quantitative Requirements for MIL STD 1797
As initially issued, Military Flying Qualities Specification for Piloted Vehicle (MIL STD 1797) had qualitative PIO requirements that said, in effect, there shall be no PIOs resulting from the pilot's attempt to control the aircraft. There were also a significant number (16) of quantitative PIO-related requirements, although they were interspersed with other requirements that were not PIO-related. As a result, the PIO-related requirements did not stand out in any way.
In practice, the design goal for military aircraft is to meet Level 1 flying qualities requirements, but most aircraft demonstrate varying degrees of Level 2 flying qualities. There is no distinction among Level 1 flying qualities requirements in terms of importance. That is, each Level 1 requirement is presented as if it were of equal value to the mission objectives for the aircraft. The mission impact of the possible permutations and combinations of
individual Level 1 and Level 2 flying qualities requirements is not known. Consequently, critical PIO-related requirements are "buried" among other, less important requirements. One purpose of the interim update of MIL STD 1797 was to add quantitative requirements that specifically address PIOs.71 The update also emphasized requirements that are generally related to PIOs by calling them out again where PIO-specific requirements are presented. The quantitative Smith-Geddes requirement was added to the specification, although it only addresses linear PIO elements and is based on limited PIO data (essentially the Neal-Smith data base). These two changes are expected to result in proper attention being paid to factors that influence PIO tendencies.
Other efforts related to MIL STD 1797 include research into extending the linear PIO criteria to nonlinear PIO events. One approach is to seek a time-domain equivalent of the Neal-Smith frequency-domain criteria.4 In this time-domain approach, nonlinear PIO events are addressed by placing restrictions directly on the time histories of relevant PVS inputs and outputs. Selection of an appropriate parameter for target acquisition time is used to define aggressiveness. Currently, aggressiveness is limited by its subjective nature. Further criteria development is being pursued by several major airframe developers. This work is expected to ensure that widest possible PIO experience and data base are considered for developing and validating newly proposed requirements.
Development of Verification Maneuver Requirements by the U.S. Air Force
It is unrealistic to assume that even comprehensive and well documented criteria can eliminate PIOs. Unknown triggers may create circumstances not previously covered by the criteria. Even so, good criteria can reduce the probability of encountering PIOs. This is particularly true when they are combined with reliable evaluation techniques that expose PIO tendencies early in the development process.
Unfortunately, current evaluation techniques are not adequate for either flight testing or simulations. The selection of a sufficiently demanding task that will inherently raise the pilot's gain and frequency response has been hindered by two real considerations: safety and "realistic" flying that doesn't provoke overwhelming criticism from pilots and others outside the flying qualities community. To gain acceptance of "unrealistic" tasks as necessary for evaluating PIO tendencies, the relationship and validity of the task in question to the PIO issue must be clearly established. To this end, flight test evaluation maneuvers are being developed.
Some tasks, including HQDT (handling qualities during tracking) and capture tasks, have already been added to the updated MIL STD 1797. The new flight-test evaluation maneuvers include HQDT tasks for the following
mission tasks: air-to-air tracking, power approach, air-to-ground tracking, boom tracking, and formation flying. Clearly, HQDT and similar tasks, along with capture tasks, expose some PIO tendencies and can readily be extended to mission tasks other than air-to-air or air-to-ground tracking. An extensive discussion of the mission tasks and the HQDT version of these tasks is presented in Appendix A of the updated specification.71 Properly performed, these tasks will increase the likelihood of discovering PIO tendencies in a safe and controlled fashion.
Test maneuvers should be challenging enough to force pilot gain to maximum levels while ensuring that flight safety is maintained. This dilemma is more significant for tasks requiring large control inputs, for recovery from extreme gust upsets, or for rate limiting cases, for example. Some PIO evaluations may only be possible with ground-based or in-flight simulation tests. However, additional work will be required to determine which modifications, if any, are necessary to validate that simulated tasks are reliable indicators of PIO tendencies. Research has been initiated to address these issues.
Criteria For Assessing Other Conditions
Pilot-Aircraft Systems with Higher-Frequency Modes
The current status of APC criteria, as described in this chapter, is essentially satisfactory for assessing Category I PIO tendencies for a large class of effective aircraft dynamics. However, oscillations associated with higher-frequency modes are not covered. As Table 1-1 shows, such oscillations have occurred. Some were relatively mild, but others were severe and resulted in extreme situations involving structural failures. The latter have already required the addition of effective low-pass filtering (e.g., CH-53) or notch filtering (e.g., 777) to the PVS.
An experimental data base and appropriate pilot models can be used to estimate closed-loop characteristics for a PVS that includes flexible modes. Klyde, et al.,39 have summarized pilot-centered phenomena (e.g., closed-loop control, vibration feed through, and remnant excitation), appropriate references to experimental data, and examples of analysis for the YF-12 and a large helicopter. The techniques and data provided there can be used to examine the need for remedial measures and to assess their utility.
The frequency range over which a pilot may have a significant effect extends to 3 Hz for direct, closed-loop control and to nearly 10 Hz for vibration feedthrough and remnant excitation effects.
Non-Oscillatory APC Events
The specter of novel, non-oscillatory APC events associated with new FCS features and functions made possible by FBW technology was raised in Chapter 2. These events tend to occur in situations near control limits that create discrepancies between what the aircraft is doing and the pilot's expectations. Several features associated with non-oscillatory APC events can be noted. The first focuses on the sharing of control effectors among control axes at or near the limits of authority of the control functions. The historical antecedents for shared control include longitudinal and lateral control on elevon, ailevator, and taileron control surfaces. On some modern, high-performance aircraft, shared control is further complicated by the addition of multifunction canards, flaps, thrust vectoring, etc. Although composite control effectors are not, in principle, a consequence of FBW control technology, they are made feasible in practice by FBW technology.
The second factor associated with non-oscillatory APC events is also enabled by FBW technology. This factor is the addition of novel functions, such as gust alleviation and maneuver load control, assorted limiting features (angle of attack, speed, load factor, etc.), and operating point (accelerating trim) control. At the limits of the operational envelopes for these functions, they can modify the pilot's direct authority over the control effectors as well as give rise to transient changes in the effective aircraft dynamics.
Finally, by its very nature, a FBW FCS separates the pilot from direct mechanical connections with the effectors. Situations, such as hitting rate limits while in tight closed-loop tracking tasks, can suddenly introduce a phase lag leading to a Category II PIO event (see Chapter 2 and Appendix C). In general, the control surface position can be far behind the pilot's command without the pilot's knowledge. Upon reversal of the pilot command, the surface may even continue in the opposite direction until the surface actuation system error is reduced to zero, at which point the surface will reverse direction. For large, sharply applied, open-loop pilot commands, this control divergence can produce an effective time delay of several hundred milliseconds, as exemplified by the JAS-39 accidents.
These features combine to make PVS behavior at the margins of the control-effector/control-function envelope a multidimensional surface of bewildering complexity. In most cases in which there are large effective time delays, the pilot's perceptions will undergo two successive steps. The first is, "Nothing I do matters; I'm disconnected from the control surfaces." This is followed by a period in which the pilot attempts to sort everything out and come up with a response. Because this time can be governed by multichoice reaction time, it can last for seconds rather than milliseconds. In the second JAS-39 accident, for example, the pilot left the airplane 5.9 seconds after the start of the PIO, when the time delay had reached 0.8 sec. This shows that on an initial APC encounter, the second step in pilot perception does not come
easily. This phenomenon may underlie some of the three-dimensional PIOs described in Chapter 1. Resulting incidents and accidents will probably be ascribed to the "pilot overdriving the system."
Because there are many design choices and tradeoffs, there would appear to be no general, quantitative way to treat or assess non-oscillatory APC events that may be associated with non-harmonious limit envelopes. But design approaches can be adopted to ameliorate the situation. Thus, at one extreme, one can choose to reestablish a direct connection with the actuation system by requiring the FBW system to emulate a mechanical system. At another extreme, system logic can modify the authorities of various automatic functions as a function of the pilot's commands and the proximity to the limits, etc.
The important message here is that extremely limiting conditions on the effector and function envelope are inevitable and must be recognized and addressed, starting with a systematic and thorough examination of the myriad possible conditions that could exist near the limits of effector envelopes. Once potentially critical situations are recognized, design modifications, simulator assessments, and other methods of detecting and eliminating problematic conditions can follow.
Category II Assessments and Criteria
The conditions attending possible Category II PIOs caused by rate limiting can be identified using existing analytical and computational routines,14,15,16,17,31,39,42,62 which can provide information about the frequency, amplitude, circumstances of onset, and other characteristics of PIOs of this type.
There were two primary reasons for establishing Category II as a separate category in which nonlinear rate limiting and/or position limiting are central factors in PIOs. First, a large number of PIOs have involved rate or position limiting. Second, a relatively simple, analysis-oriented approach can lead to the discovery of PIO potential in rate limiting or position limiting situations. The more general Category III includes events associated with more complex nonlinear phenomena (other than rate and position limiting) as well as transitions in effective aircraft dynamics.
Recent attention to rate limiting PIO situations makes the analysis procedures routine. The prevalence of rate limiting as a factor in severe PIOs in flight would seem to indicate that a preliminary search for Category II possibilities is a reasonable step in checking new designs. This search can be carried out at several levels of detail, including bench tests with actual software and hardware.
Pass/fail assessment criteria for new designs are not as well developed as analytic methods intended to discover possibilities, but a promising start has been made.15,16,17 The approach used in these studies is to define a forbidden
region in the gain/phase domain. The boundaries for this region are based primarily on an examination of a large number of configurations that exhibited Category II PIOs when the onset frequency appeared within those boundaries (Figure 6-10). The rate-limiting onset frequencies and the linear system characteristics are then used together to locate the possible onset of rate limiting on the gain/phase plot. Locations inside the forbidden region are PIO-prone. The concept is fundamentally sound, but the details currently depend on certain assumptions about the details of the PVS. Pilot-vehicle simulation studies to validate these assumptions have not yet been done.
Conclusions
In addition to the major findings and recommendations listed in Chapter 7, the committee generated a number of conclusions regarding APC design assessment criteria. The available Category I criteria contain a mix of complementary elements that can be used to highlight the importance of APC issues at many levels within design, development, and test organizations. In the current environment of substantial computational resources, it is reasonable and prudent to use all available criteria through the analysis phases of design. During subsequent design, development, and test phases, partial assessments can be made using the most convenient tools for the task at hand, interpreted in

Figure 6-10
Tentative forbidden zones for Category II PIOs. Source: Duda.15
the context of the more complete data set available from the analysis phases. For example, dropback as a time-domain measure might be more convenient for assessing flight test tasks than the more elaborate frequency sweeps required for Aircraft-Bandwidth/Phase Delay or other frequency-domain measures.
Some of the F-16 and YF-22 control system parameters have not correlated well with some available criteria. Yet the YF-22 test pilots were very pleased with the aircraft's handling qualities. This anomalous history should be taken into account when criteria are chosen and the control system structure is selected. Even so, the structure of the F-22 control system has been redesigned to better correlate with handling qualities and APC criteria.
It would be prudent for designers to consider more elaborate analyses, simulations, and tests if most initial approaches show even marginal APC potential. Designers should also recognize that all available criteria assume that the effective controlled element gain is optimized. In addition, designers should remain sensitive to the risk posed by Category II and III APC events, even if available criteria indicate satisfactory performance with respect to Category I APC events. For example, design assessments should search for situations that may encourage non-oscillatory APC events caused by a lack of harmony between pilot expectations and control system actions, especially in situations that are on or near the margins of control-effector/control-function envelopes.
The Aircraft-Bandwidth/Phase Delay and ω180/Average Phase Rate criteria can be determined unambiguously only if flexible modes and/or quadratic dipole pairs appear only at frequencies well above 2ω180. A shortcoming with the Smith-Geddes Attitude-Dominant Type III criterion in its current formulation is that, on occasion, an artistic interpretation must be made to determine the amplitude-ratio slope (m).
The Smith-Geddes Type III criterion tends to be over conservative, sometimes warning of PIO susceptibility when experience has shown it to be unlikely. However, an aircraft that clears the Aircraft-Bandwidth/Phase Delay, Smith-Geddes Type III, and Gain/Phase Template criteria will have minimal risk of experiencing Category I APC events.
Two combinations of criteria are particularly useful for conducting pass/fail assessments of susceptibility to Category I APC events: (1) Dropback plus Aircraft-Bandwidth/Phase Delay criteria, and (2) Dropback plus Gain/Phase Template, including ω180/Average Phase Rate. These combinations can help designers to distinguish which aircraft are prone to Category I APC events. They are also directly useful for designing aircraft to avoid APC.
It is relatively easy to estimate the frequency region for Category I PIOs. The Smith-Geddes Type III criterion seems to provide a useful upper bound on PIO frequency. The synchronous-pilot frequency (i.e., the −180 degree phase frequency for the effective aircraft dynamics) may provide a lower bound.
There are several areas where available criteria need to be improved. For example, the Smith-Geddes Type III frequency formulation should be fine tuned to take more current data into account. This would make the Smith-Geddes Type III criteria less restrictive and thus a better discriminator on a pass/fail basis. Similarly, Aircraft-Bandwidth/Phase Delay boundaries should continue to be reviewed and adjusted to accommodate new data. Also, because of the unique insights offered by the Neal-Smith criteria, the recent promising modifications to them should be extended and exploited.
The utility of available criteria could also be improved by more fully exploring the effects of angular and linear accelerations, as well as other non-attitude-sensitive cues, on sensitivity and susceptibility to Category I APC events. There is some evidence that these cues have a second-order, yet beneficial, impact. If this is true, the existing attitude-dominant measures and criteria may suffice only as conservative criteria. Normal acceleration at the pilot's location has long been considered to be an important or even central cue in closed-loop oscillatory behavior. Indeed, the Smith-Geddes Type I theory (which this report does not address) offers an elementary criterion for assessing acceleration feedback effects on PIO susceptibility that should be checked for completeness.66
Additional research is especially important on design assessment criteria for Category II and III PIOs and non-oscillatory APC events. This research should include experiments and the development of new analysis methods. Promising Category II assessment criteria, in particular, should be subjected to experimental verification.