J
Probabilistic Dependencies in Combat Models
Paul K. Davis, RAND and the RAND Graduate School
BACKGROUND
One special request made to the panel preparing this report was for comments on the importance of configural models for mine warfare and, perhaps, for other classes of combat. The request reflected a decades-long controversy on how to represent mine and countermine warfare issues mathematically so that the models would be of value to the acquisition, training, and operations communities. The term configural model is associated with a series of studies using complex analytical probabilistic models, which account for many of the probabilistic dependencies that appear in mine warfare problems (Horrigan, 1991). 1 In a number of cases with real-world importance, the associated effects are quite large and cannot be accommodated by simple adjustment of planning factors. It is puzzling that there should still be controversy about the need to account for the effects explicitly. Discussion of the mine warfare issues is included in a separate panel report on undersea warfare (Volume 7 of the nine-volume series, Technology for the United States Navy and Marine Corps, 2000-2035: Becoming a 21st-Century Force), but in this report it seemed useful to point out that the issues are of a class that can be found throughout DOD. The need to account for such
|
1 |
See, e.g., Horrigan (1991). Horrigan defines configural theory as “a mathematical theory for quantifying the relationships between the behavior of weapons in use in combat and their individual characteristics. Its principal purpose is to provide concepts and mathematical relationships to improve our understanding both of weapon behavior in combat and of combat effectiveness. Its name is derived from its central concept, configuration, which is the mathematical expression of the fact that the disposition in space and time of the targets and weapons of the attacker and the defender is inseparable from the outcome of the engagement and the combat effectiveness of those weapons.” |
dependencies or correlations is well understood scientifically and mathematically, 2 but many DOD models do not do so adequately. In what follows we give examples of such effects from other domains, primarily to illustrate their generic character and to thereby increase acceptance of the need to address them.
CLASSIC EXAMPLES OF CORRELATED EFFECTS IN COMBAT MODELS
The Fratricide Problem in Strategic Nuclear Warfare
In the mid-1970s, an important military issue was whether emerging Soviet ICBMs would be able to destroy U.S. Minuteman ICBMs in their silos. The answer depended heavily on the effects of targeting a given silo with two (or more) reentry vehicles, since neither accuracies nor reliabilities were high enough to assure high probabilities of kill with a single RV.
The naive calculation was to assess the probability of a silo's destruction D by n RVs as follows:
D = 1 - (1 - RPk)n,
where R is the reliability of a single RV and Pk is the single-shot kill probability for a reliable RV attacking a given silo (a function of the RV's accuracy and yield, and the silo's characteristics). The equation treats the RVs as independent. The second term is the probability that n independent RVs fail to destroy the silo.
The first problem with the naive calculation is that the reliability of a given RV is correlated with the reliability of its sister RVs on a given ICBM: the principal failure mode was not in fact the RV, but the missile. Thus, if a missile failed, all of its RVs would fail. As a result, it was often assumed that a nuclear attack plan would “cross-target” weapons so that a given silo would be attacked by RVs coming from different missiles. In that case, for two RVs the equation would be
D = 1 - (1 - RPk)(1 - RPk).
In reality, the problem is much more complicated because the effects of the successive RVs are not independent: the first RV, if it arrives and detonates, may create shock waves and send dirt and other debris into the air through which the second RV must penetrate. On the other hand, partial damage from the first RV may reduce the strength of the silo to a second, and so on. On a larger scale,
|
2 |
In statistical mechanics, the term “correlations” is often used to mean what we refer to here as “probabilistic dependencies.” In some fields, however, “correlations” refer to only a subset of the many possible dependencies. Thus, we have avoided the term here. |
detonations at one silo could affect the environment seen by newly arriving RVs at relatively distant silos. If such effects degraded the effectiveness of the second and subsequent RVs, then one referred to “fratricide.”
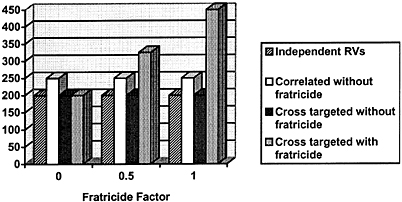
FIGURE J.1 Effects of fratricide.
The issue was important at the time because estimates were that the probability of destruction was high (e.g., 90 percent) if the fratricide effects were small. Figure J.1 shows the difference between the independent-event calculations and a calculation accounting for fratricide. It assumes a reliability of 0.85, a single-shot kill probability of 0.65, and 1,000 silos. The expected number of surviving ICBMs more than doubles if fratricide is strong.
This calculation treats the probability of fratricide as a mere parameter, but where did the value come from? A number of scientists attempted estimates of the fratricide effect, but the most insightful work was probably that accomplished with detailed simulations that considered flight dynamics, shock waves, the nature of the dust cloud, the characteristics of the RVs themselves (ruggedness, ballistic coefficient, and so on), and the spatial configuration over time of both targets and attacking RVs. Even first-rate minds, when attempting to understand the problem analytically and physically, failed to account for what turned out to be major effects.
One lesson from this work was the value of combining both analytical work (relatively simple models of the phenomenon designed primarily to structure the issues) and detailed simulation. Another lesson was that the mathematics of the calculation mattered.
Saturation Effects in Ballistic Missile Defense
Scientists involved with ballistic-missile defense have recognized for decades that the Achilles' heel of many defenses is the ability of the attacker to
saturate them. Even if a defense battery is reliable and effective (big ifs, to be sure), it has a limited capacity for handling multiple targets and a limited inventory of surface-to-air missiles. It can be overwhelmed.
This has been known to be important in ballistic-missile defense calculations for at least three decades. Indeed, it is the principal reason that scientists have generally been pessimistic about the feasibility of an adequately effective one-layer defense. For example, if one tried to defend an aircraft carrier against nuclear-armed ballistic or cruise missiles, the effort would be hopeless against an opponent able to defeat the local defenses, something that typically requires many fewer weapons that one might think because of leakage.
There are many other “configural effects” in BMD. For example, if early warning radars can “warn” smaller-area radars of incoming weapons, then the defenses can be much more effective. But the early warning radars are then a critical node: that is, there are strong dependencies between terminal-defense capability and the continued existence of the early warning radars.
Gaming Effects
Yet another “configural effect” in ballistic missile defense involves the game theory of tactics. Suppose that there are 10 targets to be defended with 10 perfect interceptors. And suppose there are 10 perfect attacking missiles. How should the defending missiles be allocated among targets? How should the attacking missiles be allocated? If the defender has one missile for each target, then the attacker can destroy 5 targets with confidence by merely double-covering half of the set. Knowing that, how should the defender defend? Variants of this can be a complex game theory problem with nonintuitive results a factor of two or so different from what one might naively expect (or infinitely different in the example, where the number of targets killed could be 5 instead of 0).
Concentration and Counter-concentration in Operational-level Ground Combat
Although corps- or theater-level ground combat may not seem to involve configural problems because of its much higher aggregation, it does. The attacker does not attack uniformly, and the defender, if able to do so, responds nonuniformly to events. If one tries to calculate attrition, movement, or even cruder measures such as “who wins in a given corps sector?”, and if one tries to use overaggregated equations that feature the overall force ratio, the results are nonsense. The attacker will concentrate and create a large force ratio in his main corridors. If the defender is fast enough, he will “reequilibrate, ” but if the attacker is fast enough, he will break through before that happens and win the battle.
At lower levels (higher aggregation), the same phenomenon occurs, but the
time scales are different. It is often believed by army officers that “reequilibration” is feasible—on average—at, say, the battalion level. That is, if one battalion is broken through by a locally concentrated force, then brigade and division-level reserves are supposed to come in and stem the breach. That is what command and control is all about for ground forces. But it may not happen that way. While aggregate models like Vector, TACWAR, and JICM do not represent this explicitly, the defender might lose at a force ratio that “ought” to be sufficient because the defender is unable to counter-concentrate quickly enough. In entity-level simulations like Janus, this is easier to see perhaps, and if one introduces statistical distributions, then many interesting things become visible. On the other hand, if one understands this well enough, one can reflect it in the higher-level aggregate models by calibrating the equations so that “break-even” occurs at a smaller force ratio than the naive calculation would suggest. This is not enough, however, if one wants to pay attention to probabilities. And so on. All of this has been understood to some extent conceptually for a long time. However, many of the configural effects have not been built in except at the entity level, where it is hard to avoid doing so (Davis, 1995b). Even there, workers too often focus on expected-value results rather than examining the probability distribution of results, which may in fact be multimodal.
DISCUSSION
These examples demonstrate that the configural effects noted in mine warfare theory are not only real, but akin mathematically to effects long recognized as fundamental in other domains of defense analysis. It should not be controversial to observe that proper modeling of combat must account adequately for probabilistic dependencies. 3 In mine warfare (and also in subjects such as penetration of air defenses), this is typically not understood intuitively because, for example, the n-th ship going through a mine field may be independent of the previous n - 1 ships, thus suggesting validity of an independent-events calculation. The subtlety here is that the minefield through which the ships move does not change significantly from ship to ship. Thus, the penetration probabilities are correlated (i.e., there are probabilistic dependencies). The resulting probability distributions have been shown by Timothy Horrigan to be distinctly multimodal in many real-world cases, and not at all like what one might expect from a primitive treatment of probabilities. Working the problem correctly can have large effects on both weapon requirements (how many to buy) and operational assessments during war.
Unfortunately, there are numerous cases throughout defense analysis where
|
3 |
These examples do not do full justice to the range of effects treated in Horrigan (1991) and elsewhere, but they may demonstrate the ubiquity of dependency issues. |
probabilistic dependencies are not accounted for properly. There are many reasons, including simplicity and familiarity of naive independent-event calculations, which many people can perform adequately with a spreadsheet. A deeper reason is that untutored intuition is often poor on issues involving probabilistic calculations. Indeed, probabilistic effects are sufficiently nonintuitive that workers often revert to simplified and naive calculations (including deterministic calculations when they are clearly inappropriate) even though they were once sensitive to the subtleties.
A third reason for failure to treat dependencies is that past computing capabilities did not permit workers to handle them effectively. This, coupled with the intuitive plausibility of many correlated effects averaging out or at least greatly simplifying, led to dependence on aggregate expressions such as the Lanchester equations described elsewhere in this report. That simplification has sometimes been valid and sometimes not. The conclusion here should be that without detailed analysis, and in many cases detailed simulation akin to “experimentation” with a real system, we should be skeptical about the validity of formulations that do not treat statistical dependencies.
Where might we find instances of such problems? The answer is “in virtually every part of combat modeling.” Indeed, whenever calculations of effects such as attrition are effectively multiplying together a set of planning factors, the effect is to assume an independence of events that may not be correct. Current-day assessment of precision-strike effectiveness against an invading army is a prime candidate for errors.
CONCLUSIONS
The panel was asked a number of questions about configural effects in mine warfare. It was surprised that there continues to be controversy about the importance of treating correlation effects such as those that are manifest in mine warfare. When two ships move through a mine field, the mines do not re-randomize their locations between ships. Nor do the ships move independently (e.g., one may follow the trail of another). Nor, in fact, is the pattern of mines in a given waterway random in many circumstances. And so on. The probabilistic effects reported for mine warfare are real, and Navy doctrine and decision aids for dealing with mine and countermine warfare should reflect them. This is without prejudice to how that is accomplished, since there are a variety of possible modeling approaches. In particular, one approach is analytical and has advantages for moving from requirements (e.g., a maximum loss rate to mines) to estimates on how many mines to buy or how to lay them. A second approach involves simulation, which has many advantages (and is in some respects easier), but which is not easily able to answer the questions analytical models are best for. Also, analytical models and the related theory can clarify the structure of the problem so as to illuminate the dependence on controllable variables.






