Page 264
10
Statistical Issues
This chapter addresses some of the statistical issues related to characterizing the dose-response relationship between cancer incidence and exposure to arsenic in drinking water. The chapter comprises five major sections. The first reviews the broad principles of dose-response modeling and discusses how age effects can be incorporated into the risk-assessment process. The second section briefly summarizes the approach used by the U.S. Environmental Protection Agency (EPA) in its 1988 arsenic risk assessment based on the skin-cancer data reported by Tseng et al. (1968). This section elaborates on some of the sources of uncertainty associated with the 1988 risk assessment, which was reviewed in Chapter 2. Much of the uncertainty comes from the fact that the Tseng study was "ecological": Instead of having individual measurements of arsenic exposure, subjects were assigned exposures according to the village where they lived. The third section presents a description of the problems associated with risk assessment based on ecological data. It also discusses the kind of measurement error that arises in this context and its implication for risk assessment in general, as well as specifically for the analysis of the Tseng data. The fourth section presents some empirical analysis based on cancer mortality data from Taiwan. This analysis should not be interpreted as a formal risk assessment for arsenic in drinking water or as a recommendation on how the risk assessment should be performed. Rather, it is presented only to illustrate points raised earlier in the chapter. The fifth section provides a discussion of some of the different statistical approaches that can be applied to disease mortality data for quantitative risk assessment. In particular, the section discusses some advantages and disadvantages of modeling age effects directly as well as modeling via standardized mortality ratios; the latter requires specification of an external baseline comparison or control group.
Page 265
A Review of Dose-Response Modeling and Risk Assessment
Dose-response modeling refers to the statistical problem of characterizing the probability of the occurrence of an event as a function of exposure. For simplicity, the discussion here will refer to the event of interest as "cancer." In practice, there are always subtleties and complicating factors to consider when performing a specific risk assessment. The purpose here is not to address all these issues but to outline the broad principles of model fitting and quantitative risk assessment. The one issue that the subcommittee does address in some detail is how to incorporate information on age-specific cancer rates into the risk-assessment process.
Suppose we have data from N individuals corresponding to their exposure and cancer status. More precisely, let yi take the value 1 if person i has cancer and 0 otherwise. Let xi be the exposure concentration for that same person. Then, if pq(x) represents the assumed dose-response model that characterizes the probability of cancer as a function of exposure through a set of unknown parameters q, the maximum likelihood estimator (MLE) of q is the value that maximizes the likelihood
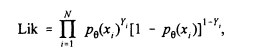
(1)
where Õ denotes product. As discussed in Gart et al. (1986, Ch. 5), many dose-response models are available that can be used to describe the relationship between exposure and cancer prevalence. EPA often uses the multistage model (Holland and Sielkin 1993) in the analysis of animal data. That model, which is motivated by the idea that cancer occurs as the last of several irreversible steps, takes the form
![]()
(2)
where Q0, Q1, . . . Qk are elements of the unknown parameter vector q, which needs to be estimated using maximum likelihood. Usually, the parameters are estimated under the constraint that the Q's are non-negative. Often, K is taken to equal 1 (the 1 hit model) or 2.
In the past, the next step after fitting the dose-response model has been to estimate the exposure concentration that corresponds to an "acceptable" risk
Page 266
above background. The acceptable risk level for cancer risk assessment has historically been 10-6, however, the recent proposed EPA (1996) guidelines have moved away from the idea of extrapolating to such low risks. Instead, the proposed default approach is to estimate a "point of departure," which is the dose corresponding to a risk level within the observable range of data. For animal studies, the 1996 guidelines suggest that the 10% excess risk level will typically provide an appropriate point of departure that can be estimated without significant extrapolation. For epidemiological studies, however, a lower level (1% or 5%) is usually more appropriate (see EPA 1996, p. 17962). Regardless of whether the goal is low-dose extrapolation or estimation of a point of departure, the statistical methods are the same, namely, solving for the value of x that solves p(x) - p(0) = r, where r represents the excess risk level of interest. To allow for statistical variability in estimating unknown model parameters, it is typical to calculate a lower confidence limit on this value. Gart et al. (1986) discussed various methods of calculating confidence intervals for the dose corresponding to a specified excess risk above background. As described in the EPA 1996 guidelines, a popular approach is to calculate an upper 95 % confidence limit on the estimated dose-response curve itself, and then to identify the exposure x that corresponds to the desired excess risk on this curve. Standard maximum-likelihood methods can generally be used for this purpose when the assumed dose-response model is differentiable and involves no constraints on the parameter space. Calculating confidence limits becomes more complicated for the multistage model because of the non-negativity constraint on the Q's. Guess and Crump (1978) discussed approaches to obtaining confidence intervals based on the multistage model.
Dose-response modeling becomes more complicated when the data also include information on age. The basic approach depends on whether the end point of interest is presented in the form of incidence or prevalence data. The skin-cancer data used in the 1988 EPA risk assessment were in the form of prevalence (the proportion of subjects with the disease among those alive at each particular age). The data on internal cancers, to be discussed later, are summarized as mortality data (the number of subjects who die from the disease at a certain age, along with the person-years "at risk" at that same age). This section focuses on the analysis of prevalence data. Modeling strategies for incidence data will be discussed later.
From a statistical perspective, it is straightforward to extend dose-response functions to include age and other factors. The multistage Weibull model is such an extension of the multistage model and takes the form
Page 267
![]()
(3)
where x represents exposure concentration, t represents age, and pq(x, t) represents the probability of cancer in an individual aged t exposed to concentration x. Note that as above the value k = 2 is commonly used. The parameters Q0, . . . Qk, T0, and C represent the elements of the unknown parameter vector q, which needs to be estimated using maximum likelihood. As above, q is usually estimated under the constraint that the Q's are positive. Equation 3 implies that the probability of cancer for a fixed age follows a multistage model; for a fixed exposure, the model implies that a person's age at the time of developing skin cancer follows a Weibull distribution.
The step after model fitting is calculating the exposure concentration that corresponds to a specified excess risk above background. This step is more complicated when an age-adjusted model has been used. A typical approach (illustrated in the next section) is to convert to a lifetime risk of cancer by summing the values of pq(x, t) over all values of t, weighted by the proportion of the population alive at each age. Standard methods can then be applied to obtain confidence intervals. Again, the theory becomes more complicated for the multistage Weibull model, because the Q's are constrained to be nonnegative, and Pq (t, x) is not differentiable everywhere with respect to T0.
The EPA 1988 Analysis
As described in Chapter 2, the data used by EPA in its 1988 risk assessment for arsenic in drinking water came from an epidemiological study by Tseng et al. (1968). The study was based on a cross-sectional assessment of the entire population (40,421 people) from 37 villages in a region of Taiwan where artesian wells with high arsenic concentrations had been in use for a long time. For comparison, 7,500 inhabitants from a control region were also studied. Subjects were examined for various skin lesions and skin cancer. Water samples (142 in total) from 114 wells (110 artesian and 4 shallow) were analyzed and found to have arsenic concentrations ranging up to 1.8 ppm. Individuals were assigned to exposure categories according to their village of residence. Villages were divided into three exposure groups: low (less than 0.3 ppm), medium (0.3-0.6 ppm), and high (more than 0.6 ppm) arsenic concentrations. A fourth category of "undetermined" was assigned to villages either where wells had been closed or where the variability was so great that
Page 268
it was impossible to reliably assign the village to an exposure category. Subjects were also classified into four age groups: 0-19, 20-39, 40-59, and 60 and over. Tables 10-1 and 10-2 (EPA 1988) show the data reported in the Tseng study. EPA fitted the multistage Weibull model to the data, omitting the undetermined exposure category and using the value k = 2. To use the fitted dose-response model to estimate risk for the U.S. population, several additional calculations were needed. In particular, it was necessary to adjust for differences between the U.S. and Taiwanese populations with respect to (1) age-specific mortality, (2) body weight, and (3) water-consumption rate. To account for mortality differences, the age-specific dose-response curve was translated to a lifetime cancer risk for the U.S. population by multiplying the estimated age-specific probabilities of having developed cancer by the U.S. Life Tables (NCHS 1998) death probabilities:
![]()
where q, is the probability of dying at age t in the United States, and St denotes summation over all age groups. To adjust for differences in weight and drinking rates, EPA assumed that a typical Taiwanese male weighed 55 kg and drank 3.5 L of water per day. A typical Taiwanese women was assumed to weigh 50 kg and drink 3 L per day. A typical U.S. reference person (male or female) was assumed to weigh 70 kg and drink 2 L per day. Assuming that the cancer risk is related to micrograms ingested per kilogram of body weight, it follows that a typical U.S. male drinking water contaminated with arsenic at x µg/L would have the same age-specific cancer risk as a Taiwanese male exposed to 0.45x µg/L. Using this approach, EPA estimated the U.S. lifetime skin cancer risk associated with a drinking-water concentration of 50 µg/L as 1 x 10-3 for females and 3 x 10-3 for males.
Sources of Uncertainty in the EPA 1988 Analysis
As discussed in Chapter 2, several complicating factors and sources of uncertainty affect the reliability of the current EPA risk estimate. Some of the issues are generic ones common to any risk assessment. Such issues are suitability of the chosen dose-response model, choice of end point, and whether and how to address biological considerations, such as detoxification and clearance. However, some issues are specific to this particular analysis.
Page 269
One concern was that the study was ecological in nature, and such studies are often felt to be problematic for the purpose of quantitative risk assessment (NRC 1991). Although arsenic concentrations were measured at the village level, the data were further summarized into low-, medium-, high- and undetermined-exposure groups. Another problem was that only the marginal age distributions were reported, so that the information in Tables 10-1 and 102 is based on estimated rather than actual data.
The following section discusses some of the implications, in general and specifically for the Tseng study, of using ecological and grouped data for dose-response modeling and risk assessment.
Problems With Risk Assessment Based On Ecological Data
Many authors have discussed the shortcomings of assessing dose-response relationships based on ecological data (e.g., see Greenland and Morganstern 1989; Greenland and Robins 1994). Among the concerns in such settings is the potential for bias due to unmeasured confounders. Ecological studies are most problematic when the groups being analyzed are very heterogeneous. That would be the case, for example, if one were to measure arsenic concentrations for every county in the United States and then try to correlate those concentrations with county-specific cancer rates. County-to-county variation in income, urbanization, air pollution, and other factors would most likely
| TABLE 10-1 Estimated Distribution of the Surveyed Male Population at Risk (Skin-Cancer Cases) by Age Group and Concentration of Arsenic in Well Water in Taiwana | |||||
| Arsenic | Age Group, yr | ||||
| Concentration, ppb | 0-19 | 20-39 | 40-59 | ³60 | Total |
| Low (0-300) | 2,714b (0)c | 935 (1) | 653 (4) | 236 (11) | 4,538 (16) |
| Medium (300-600) | 1,542 (0) | 531 (2) | 371 (18) | 134 (22) | 2,578 (42) |
| High (>600) | 2,351 (0) | 810 (18) | 566 (56) | 204 (52) | 3,931 (126) |
| Undetermined | 4,933 (0) | 1,699 (3) | 1,188 (61) | 429 (64) | 8,249 (128) |
| Total | 11,540(0) | 3,975 (24) | 2,778 (139) | 1,003(149) | 19,296 (312) |
| aFor the control group, the number of persons in the age groups 0-19,30-39,40-59, and 260 are 2,679, 847, 606, and 176, respectively. No skin cancers were observed in the control population. | |||||
| bEstimated number of persons at risk. | |||||
| cEstimated number of skin-cancer cases observed. | |||||
| Source: Adapted from EPA 1988, Table B-1. | |||||
Page 270
| TABLE 10-2 Estimated Distribution of the Surveyed Female Population at Risk (Skin-Cancer Cases) by Age Group and Concentration of Arsenic in Well Water in Taiwana | |||||
| Arsenic | Age Group, yr | ||||
| Concentration, ppb | 0-19 | 20-39 | 40-59 | ³60 | Total |
| Low (0-300) | 2,651b (0)c | 1,306 (0) | 792 (3) | 239 (2) | 4,988 (5) |
| Medium (300-600) | 1,507 (0) | 742 (1) | 450 (9) | 136 (8) | 2,835 (18) |
| High (>600) | 2,296 (0) | 1,131 (4) | 686 (33) | 207 (22) | 4,320 (59) |
| Undetermined | 4,819 (0) | 2,373 (2) | 1,440 (13) | 435 (27) | 9,067 (42) |
| Total | 11,273(0) | 5,552(7) | 3,368(58) | 1,017 (59) | 21,210 (124) |
| aFor the control group, the number of persons in the age groups 0-19,30-39,40-59, and ,60 are 2,036, 708, 347, and 101, respectively. No skin cancer was observed in the control population. | |||||
| bEstimated number of persons at risk. | |||||
| cEstimated number of skin-cancer cases observed. | |||||
| Source: Adapted from EPA 1988, Table B-2. | |||||
cause bias in such an analysis. However, such issues are unlikely to be a serious problem for the Taiwanese analysis. The study region is relatively small, according to Tseng et al. (1968), a ''limited area on the southwest coast of Taiwan. " The region is also fairly homogeneous in terms of lifestyle: most inhabitants are engaged in farming, fishing, or salt production. Little variation in diet and a low degree of urbanization occur there.
Besides the potential for confounding, a second concern with ecological studies is the lack of individual exposure assessment. Instead of assigning individual-level exposures, an ecological study assigns individuals to exposure categories based on aggregate exposure concentrations measured for the group to which the individuals belong. As a result of assigning exposure in that way, ecological studies are subject to a type of measurement error.
It is well known that measurement error in exposure variables can lead to biased estimates of dose-response parameters and underestimation of the variance of estimated model parameters (Carroll et al. 1995). For the sake of illustrating the ideas, suppose that we are interested in fitting a simple linear model that relates arsenic concentration to a health outcome. Suppose xi represents the true arsenic exposure for the ith person in the study. The problem is that instead of being able to accurately measure the true xi for this person, our observed measurement (say, wi) is contaminated with error. Theory has been developed for two broad classes of measurement-error settings. In the classical measurement-error setting, we can think of the observed value wi as corresponding to the true exposure xi plus some independent random error, wi = xi + ei. Such an error structure could occur, for
Page 271
example, in a study design that attempted to assess each subject's average exposure concentration, say, by recording individual drinking patterns over a period of time. The error might arise, for example, through inaccuracies in recording individual drinking patterns or through laboratory and other errors in measuring the arsenic concentrations in the wells from which each person was drinking. The second broad class, the Berkson measurement-error model, occurs in settings where individual exposures are estimated by assigning to individuals the exposure value measured for the group to which the individual belongs. In contrast to the classic setting described above, here one can express the true exposure concentration xi as the measured average concentration wi plus random error (xi = wi + Îi). An argument can be made that the Berkson model applies in the Tseng study because individuals were assigned an exposure concentration based simply on the average concentrations measured in their villages. The error here would correspond to individual departures from the village mean exposure concentrations, due to variations among wells within a village, individual drinking habits, and so forth. If the Berkson measurement-error model applies and the outcome of interest follows a linear model involving the true exposure concentration, then it is well known that fitting the model naively with xi replaced by wi will lead to valid estimates of the regression parameters from this true model, although variances might be incorrectly estimated.
It is tempting to apply the above logic and conclude that one does not need to worry about bias from a dose-response model applied to ecological data, and in certain settings, such an argument is sound (Prentice and Sheppard 1995). There are several reasons why caution is needed, however, in extending that logic to settings such as the one described by Tseng. First, the effect of Berkson measurement error on inference for nonlinear models, such as the multistage Weibull, has not been widely studied. Although one would expect that approximately the same principle would apply, some bias will generally exist (see Carroll and Stefanski (1990) for further discussion). More critical is that fact that validity of regression analysis under the Berkson measurement-error setting requires the strong assumption that the mean exposure concentration for each group has been measured without error. When that assumption is violated, the resulting estimates are likely to be biased, just as in the classical measurement-error setting. In terms of the analysis of the Tseng data, that means that the results will only be reliable if the appropriate representative values are chosen for the low-, medium-, and high-exposure groups. In the case of the arsenic risk assessment, the fact that the well-water concentrations could vary over time and that some villages had more than one well makes it
Page 272
difficult to place much confidence on any one choice for representative concentrations for the low-, medium-, and high-exposure groups. For example, the values used by EPA were 170 ppb, 470 ppb, and 800 ppb. However, other values could also be justified. To assess the impact of choosing different representative values for the concentrations in the three broad exposure groups, the multistage Weibull model was refitted to the data in Tables 10-1 and 10-2 by using some different choices for the representative concentrations in the three exposure groups. The results, summarized in Table 10-3, suggest that varying the assumed representative concentrations has only a moderate effect on the estimated risk of skin cancer associated with exposure to arsenic at 50 ppm of drinking water. However, the estimated risks remain at the same order of magnitude, ranging from 1.5 to 5.1 cancers per 1,000, for the representative values shown in the table. One might also explore the effect of varying the choice of the representative ages chosen to represent each of the four age categories. In Table 10-3, the values used were the same as those used by EPA in its 1988 analysis: 8.45, 30.19, 49.42, and 69.15. As was the case with the representative exposure concentrations, varying those values is likely to have only a moderate effect on estimated risk levels.
The measurement error theory described in this section and the results presented in Table 10-3 suggest a certain robustness of the risk assessment conducted by EPA using the Tseng data. Ideally, however, it would be useful to have access to more detailed exposure data so that the effect of grouping could be addressed more directly. The internal-cancer data discussed in the
| TABLE 10-3 A Sensitivity Analysis Obtained by Varying the Assumed Representative Exposure Concentrations of Arsenic in the High, Medium, and Low Groups for the Tseng Data | ||
| Arsenic Concentration, ppba | ||
| (Low, Medium, High) | Estimate of Risk per 1,000b | Upper Boundc |
| 170,470,800 | 2.5 | 4.2 |
| 128,466,700 | 3.2 | 5.1 |
| 100,400,750 | 5.1 | 7.1 |
| 200,450,750 | 1.5 | 3.2 |
| 100, 500, 800 | 4.4 | 6.3 |
| aControls assumed to have zero concentrations of arsenic. | ||
| bSkin-cancer risk per 1,000 Taiwanese males aged 62.5 years, exposed from birth to drinking water with arsenic concentrations of 22 ppb (U.S. equivalent, 50 µg/L); assumed ages within each group: 8.45, 30.19, 49.42, 69.15 yr. | ||
| cBased on a 95% upper confidence interval obtained using the program MULTWEIB available from ICF Kaiser. | ||
Page 273
next section have exposure concentrations reported separately for 42 villages and, hence, are more useful for this purpose. It is important to remember, however, that the discussion here is about the effects of grouping on the robustness of a particular fitted model. The ideal situation is to have reliable individual exposure assessments. Whenever data are grouped, there is the possibility of obscuring the true shape of the dose response curve.
Internal-Cancer Data From Taiwan
Tseng's 1968 report on skin-cancer data has generated ongoing interest in characterizing the risks associated with arsenic exposure not only in Taiwan but in several other regions of the world (see Chapter 7). This section describes in more detail some mortality data on several internal cancers, including bladder, lung, and liver, for the arsenic endemic region of Taiwan. Although we will also present some dose-response analysis of these data, it is important to emphasize again that the results are not to be interpreted as a formal risk assessment, or as an endorsement of these data for the use of risk assessment for arsenic in drinking water. Rather, we present selected results to illustrate some of the issues that arise in the context of trying to characterize the dose-response relationship of arsenic exposure based on ecological data.
The data are from a study of the population of 42 coastal villages in six southwestern townships including Peimen, Hsuechia, Putai, Ichu, Yensui, and Hsiaying where blackfoot disease is endemic (see Wu et al., 1989, for further discussion). The data were described in a letter by Chen et al. (1988), grouped into three arsenic concentrations (less than 300 ppb, 300-590 ppb, and 600 ppb and over), and weighted by person-years of exposure at each concentration reported by Wu et al. (1989). Two dose-response assessments based on those data appeared about the same time (Chen et al. 1992; Smith et al. 1992), although the data sources were summarized differently. In particular, Chen and colleagues reported data in which arsenic concentration was categorized by four intervals (less than 100 ppb, 100-290 ppb, 300-590 ppb, and more than 600 ppb) and age at time of death by four intervals (less than 30, 30-49, 50-69, and 70 years of age and over). Smith and co-workers used age-standardized data grouped as reported by Chen et al. (1988). The Smith et al. (1992) study used data from an unexposed Taiwanese population as the basis for the age standardization.
The available data (see Addendum to Chapter 10) include the person-years at risk and the number of deaths due to bladder, liver, and lung cancer in 5-
Page 274
year age increments for each of the 42 villages. The data are summarized in Table 10-4, with villages grouped into the same high-, medium-, and low-exposure categories used in the original Tseng study. The arsenic concentrations in the 42 villages ranged from 10 to 934 ppb. Table 10-5 shows the ordered values. Table 10-5 does not show that, in some cases, arsenic concentrations varied considerably in different wells within the same village (see Addendum). Hence, there is considerable uncertainty in the data.
| TABLE 10-4 Internal Cancer Incidence by Age and by Arsenic-Concentration Groupa | ||||||||||||
| Age | Arsenic Concentration, ppb | |||||||||||
| Group, | 0-300 | 300-600 | >600 | |||||||||
| yr | pyb | ingc | bld | live | pyb | ingc | bld | live | pyb | Ingc | bld | live |
| Male | ||||||||||||
| 20-25 | 35,521 | 0 | 0 | 0 | 17,754 | 0 | 0 | 0 | 10,477 | 0 | 0 | 0 |
| 25-30 | 21,439 | 0 | 0 | 0 | 9,802 | 0 | 0 | 0 | 6,132 | 1 | 0 | 0 |
| 30-35 | 13,493 | 0 | 0 | 2 | 6,356 | 0 | 0 | 2 | 4,507 | 0 | 1 | 2 |
| 35-40 | 12,432 | 0 | 0 | 4 | 6,000 | 1 | 0 | 2 | 3,591 | 0 | 0 | 2 |
| 40-45 | 13,550 | 2 | 1 | 3 | 6,765 | 2 | 2 | 3 | 3,852 | 0 | 1 | 3 |
| 45-50 | 13,395 | 4 | 0 | 5 | 6,423 | 6 | 3 | 5 | 3,823 | 3 | 2 | 5 |
| 50-55 | 11,293 | 7 | 2 | 6 | 5,507 | 5 | 4 | 3 | 3,115 | 5 | 3 | 3 |
| 55-60 | 8,934 | 7 | 3 | 10 | 4,276 | 11 | 4 | 5 | 2,482 | 10 | 6 | 5 |
| 60-65 | 7,020 | 5 | 3 | 7 | 3,431 | 10 | 4 | 4 | 1,828 | 4 | 3 | 4 |
| 65-70 | 5,229 | 7 | 5 | 9 | 2,533 | 4 | 3 | 3 | 1,148 | 4 | 3 | 3 |
| 70-75 | 3,676 | 15 | 2 | 4 | 1,695 | 8 | 5 | 1 | 748 | 3 | 2 | 1 |
| 75-80 | 2,005 | 7 | 5 | 3 | 883 | 5 | 4 | 0 | 317 | 3 | 5 | 0 |
| 80-85 | 1,190 | 5 | 5 | 1 | 643 | 1 | 3 | 1 | 159 | 0 | 1 | 1 |
| Female | ||||||||||||
| 20-25 | 27,908 | 1 | 0 | 0 | 13,131 | 0 | 0 | 0 | 8,442 | 0 | 0 | 0 |
| 25-30 | 15,107 | 0 | 0 | 0 | 6,799 | 0 | 0 | 0 | 4,546 | 0 | 0 | 0 |
| 30-35 | 11,600 | 1 | 0 | 0 | 5,145 | 0 | 0 | 0 | 3,800 | 0 | 0 | 0 |
| 35-40 | 11,932 | 0 | 1 | 0 | 5,759 | 0 | 0 | 1 | 3,612 | 1 | 0 | 1 |
| 40-45 | 13,373 | 5 | 0 | 2 | 6,774 | 3 | 0 | 1 | 4,014 | 1 | 0 | 1 |
| 45-50 | 13,109 | 3 | 2 | 2 | 6,665 | 3 | 0 | 2 | 4,114 | 4 | 0 | 2 |
| 50-55 | 11,368 | 7 | 2 | 1 | 5,708 | 4 | 3 | 1 | 3,512 | 5 | 4 | 1 |
| 55-60 | 9,241 | 3 | 4 | 3 | 4,616 | 6 | 3 | 1 | 2,571 | 11 | 3 | 1 |
| 60-65 | 7,753 | 8 | 9 | 5 | 3,732 | 4 | 3 | 2 | 1,800 | 9 | 10 | 2 |
| 65-70 | 5,998 | 10 | 3 | 3 | 2,825 | 6 | 10 | 3 | 1,201 | 3 | 4 | 3 |
| 70-75 | 4,198 | 3 | 5 | 4 | 1,907 | 6 | 5 | 1 | 668 | 2 | 3 | 1 |
| 75-80 | 2,323 | 5 | 4 | 2 | 1,154 | 2 | 2 | 0 | 352 | 1 | 3 | 0 |
| 80-85 | 1,860 | 2 | 2 | 5 | 787 | 2 | 4 | 0 | 23 | 1 | 1 | 0 |
| aData from Wu et al. 1989; Chen et al. 1992. | ||||||||||||
| bPerson-years at risk. | ||||||||||||
| cNumber of deaths from lung cancer. | ||||||||||||
| dNumber of deaths from bladder cancer. | ||||||||||||
| eNumber of deaths from liver cancer. | ||||||||||||
Page 275
| TABLE 10-5 Ordered Median Well Concentrations for Each Villagea |
| Arsenic Concentrations, ppb |
| 10, 11, 30, 32, 32, 42, 45, 50, 56, 60, 65, 73, 80, 100,110,110, 123,126, 256, 256, |
| 259, 307, 307, 350, 398, 406, 448, 467, 504, 520, 520, 529, 538,544, 599, 650, 683, |
| 693, 694, 698, 717, 934 |
| aWu et al. 1989; Chen et al. 1992. |
As with the skin-cancer data, an ecological study design was used to construct the internal-cancer data. Individual exposures were not assessed; instead, subjects were assigned the exposure concentration corresponding to the median concentration in the water from the village in which they lived. In contrast to the skin-cancer data, however, an advantage is that the data have been kept separately by village, rather than grouping them into low-, medium-, and high-exposure intervals. Although that helps somewhat, it does not alter the fact that the data are still ecological. In fact within some of the villages wide ranges were seen in the measured arsenic concentrations of individual wells (see Addendum to Chapter 10). Of the 42 villages, 20 had only one well tested. In the remaining villages where multiple wells were tested, a wide range of arsenic concentrations were measured. For example, village "0-G" had measurements taken on five wells; concentrations were from 10 to 770 ppb, and the median concentration was 30 ppb. Village "0-E" also had five wells measured. There, the concentrations ranged from 10 to 686 ppb, the median being 110 ppb. The greatest number of wells measured was 47 for village ''4-I." The variation highlights the potential for measurement error to affect the reliability of dose-response modeling. It also suggests the potential usefulness of conducting additional analysis to assess the sensitivity of the results to omission of some villages and to other sources of error in the assigned exposures. That will be done presently. First, however, we briefly address the question of how to analyze cancer mortality data of the type presented in Table 10-4.
When the data come in the form of prevalence (the number of subjects alive at various ages and exposure concentrations and the number of those with skin cancer), then a model, such as the multistage Weibull defined in Equation 3, can be fitted by maximizing the likelihood given in Equation 1. When the data are in the form of cancer mortality rates (the number who die of the cancer over a specified period and the number at risk of dying during that same time period), the analysis becomes slightly more complicated. There are basically two possible approaches. One approach is to use a comparison population to construct standardized mortality ratios. That approach
Page 276
will be described in more detail presently. An alternative is to model the cause-specific hazard (see Cox and Oakes 1984) of dying of cancer at age t for someone exposed to arsenic concentration x. The cause-specific hazard function based on the multistage Weibull model is
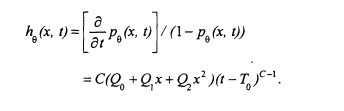
To simplify calculations, and facilitate use of life tables and death records, age is grouped into 5-year time intervals. The model can be fitted by maximizing the following likelihood:
![]() (4)
(4)
where d(x, t) is the number of people exposed to arsenic concentration x who die with cancer at age t, and r(x, t) is the corresponding person-years at risk at that age and concentration (see Laird and Olivier 1981). The products in Equation 4 are applied over the sets of all concentrations x and age groups t represented in the data set. A nonlinear optimizing routine called nlminb, available in the statistical package Splus, was used to find the value of 0 that maximizes Equation 4. That routine easily accommodates constraints and does not require differentiability of the function being optimized. Computing an estimate of the variance-covariance matrix of the estimated model parameters, however, is more difficult. Standard maximum-likelihood theory breaks down (i.e., one cannot simply invert the matrix of second derivatives) because of the constraints and nondifferentiability of the log likelihood. Various proposals have been made for constrained optimization settings in general (Self and Liang 1987) as well as specifically in the context of dose-response modeling (Guess and Crump 1978). The approach used here follows Geyer (1991), who suggests the use of the bootstrap for inference in nonstandard maximum-likelihood settings.
The results of fitting the multistage Weibull model to the three internalcancer data sets for male and females are given in Table 10-6. Both paramet-
Page 277
| TABLE 10-6 Fitted Parameters for Multistage Weibull Model | |||||
| Organ | Q0 | Q1 | Q1 | T0 | C |
| Male | |||||
| Bladder | 1.229862e-11 | 0.000000 | 7.339447e-17 | 1.470252e+01 | 5.130551 |
| Lung | 4.692041e-09 | 1.467226e-11 | 0.000000 | 2.149461e+01 | 3.919512 |
| Liver | 2.270629e-07 | 3.694680e-14 | 4.998412e-13 | 1.689983e+01 | 2.905370 |
| Female | |||||
| Bladder | 3.858906e-08 | 0.000000 | 2.222528e-13 | 3.303647e+01 | 3.473238 |
| Lung | 1.612450e-08 | 0.000000 | 6.119366e-14 | 1.709777e+01 | 3.513685 |
| Liver | 3.229792e-07 | 2.801520e-11 | 4.939496e-13 | 2.594200e+01 | 2.728167 |
ric and nonparametric bootstrap methods (see Efron and Tibshirani 1993) were applied to estimate the standard errors of the estimated parameters and yielded similar results.
Figure 10-1 shows the predicted age-specific bladder-cancer incidence rates for males from all 42 villages, based on the fitted multistage Weibull model. Each line corresponds to the predicted cancer incidence rate for a specific age group. Notice how for each age group, there is a different dose response curve. Incidence rates increase sharply with age. Once the model has been fitted, the lifetime risk of dying from bladder cancer can be calculated by using the estimated model parameters and the U.S. national census values for the age-specific death rates from all other causes. Some straightforward calculations show that the lifetime risk of dying from bladder cancer can be written as
![]() (5)
(5)
where pq(x, t) is the estimated probability of developing bladder cancer by age t for someone exposed to concentration x, and q, is the probability that a U.S. citizen dies at age t, where age is broken into the same 5-year increments used in fitting the multistage Weibull model. The values for q, were obtained separately for males and females from the Life Tables in Vital Statistics of the United States, 1994 (NCHS 1998).
The excess lifetime risk of cancer from exposure to concentration x of arsenic in the drinking water can be written as
![]() (6)
(6)
Page 278
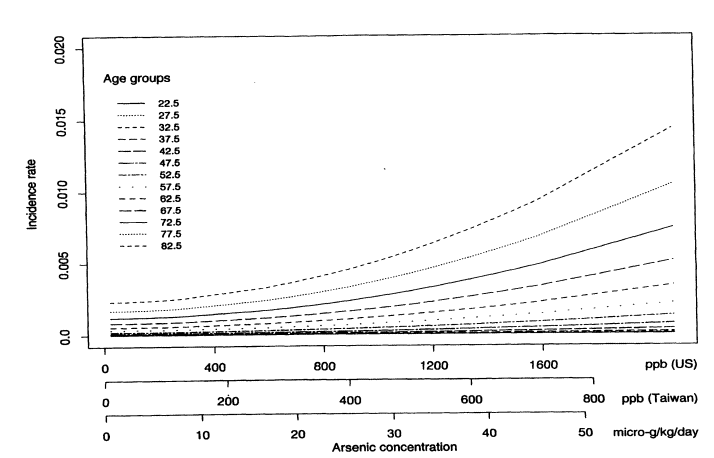
FIGURE 10-1
Predicted age-specific bladder-cancer incidence rates for males based on the multistage Weibull model.
Page 279
where Lifetime(x) is the lifetime risk of cancer for someone exposed to concentration x. Figure 10-2 shows the estimated excess lifetime risks for males of dying from bladder cancer as a function of arsenic concentration in the drinking water. The solid line shows the fitted curve, and the dotted line shows the upper 95% confidence limit, calculated using the nonparametric bootstrap. To facilitate interpretation, the x axis is labeled in three ways in terms of (1) concentration (in parts per billion) of arsenic found in Taiwan; (2) micrograms of arsenic consumed per kilogram of body weight (assuming that the typical Taiwanese male weighs 55 kg and drinks 3.5 L of water per day and the typical Taiwanese female weighs 50 kg and drinks 2 L of water per day); and (3) equivalent concentration (parts per billion) of arsenic consumed by a U.S. population (assuming that the typical U.S. male or female weighs 70 kg and drinks 2 L of water per day). Figure 10-3 shows the same plot but with the x axis drawn only to 100 ppb (based on equivalent U.S. values). Table 10-7 shows the corresponding estimated excess risks and upper 95 % confidence limits for excess lifetime risk for the U.S. population drinking water with arsenic concentrations of 10, 25, and 50 ppb. Once again, confidence limits were calculated using the non-parametric bootstrap.
Examination of the raw data suggests that variability, particularly at older ages, is large. Furthermore, several of the villages at low exposure concentrations appeared to have higher cancer rates than would be predicted from the fitted dose-response model. To assess the impact of this variability on the fitted dose-response curve, a sensitivity analysis was performed by refitting the multistage Weibull model to different subsets of villages and recomputing the estimated excess lifetime risk at 10, 20, and 50 ppb. For example, the numbers on the line labeled "single well" in Table 10-8 correspond to refitting the model excluding all the villages that had only a single well (villages 3-H, 2-I, 3-5, 3-N, 4-7, 6-A, 4-D, 3-P, 6-C, 4-8, 0-0, 4-J, 2-D, O-D, 4-M, 6-6, 3-I, 5-G, 4-P, 3-9). The results of that sensitivity analysis are given in Table 10-8. The results suggest that the risk estimates are fairly sensitive to which villages are included or excluded. For example, depending on which subset is analyzed, the estimated lifetime risk at 50 ppb can range from 0.05 to 1.6 per 1,000. At 10 ppb, the variation in estimated risk is even more marked (ranging from 0.002 to 0.324 per 1,000). Although not shown here, a similar analysis using the alternative models to be discussed in the next section did not show the same sensitivity as the multistage Weibull model.
In addition to the sensitivity of the fitted model to inclusion or exclusion of particular villages, the data provided a good opportunity to assess the effects of various degrees of grouping on the shape of the dose response. The
Page 280
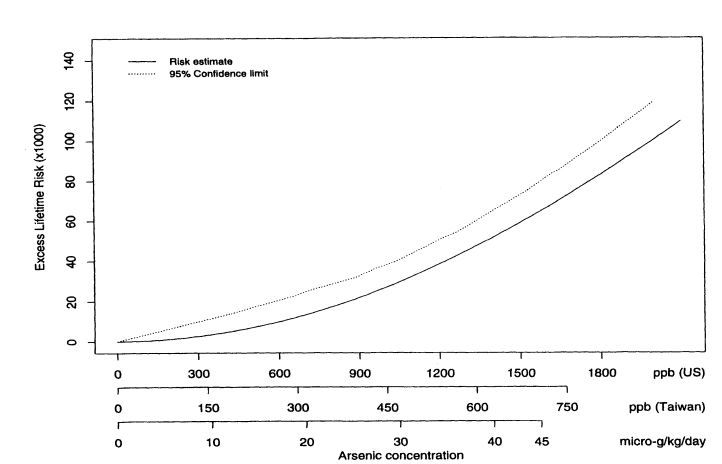
FIGURE 10-2
Male bladder-cancer rates per 1,000 people. Estimated excess lifetime risks, based on 1994 U.S. Life Tables
(NCHS 1998) for males and females, along with upper 95% confidence limits.
Page 281
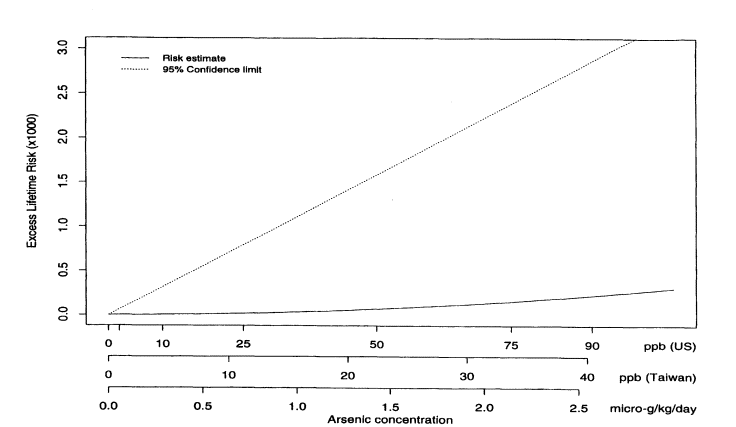
FIGURE 10-3
Male bladder-cancer rates per 1,000 people. Estimated excess lifetime risks, based on 1994 U.S. Life Tables
(NCHS 1998) for males and females, along with upper 95% confidence limits; x axis drawn only to 100 ppm
(estimated U.S. equivalent for arsenic concentrations).
Page 282
| TABLE 10-7 Excess Lifetime Risk Estimates for Bladder Cancer in U.S. Males and Females | ||
Arsenic Concentration | Excess Lifetime Risk of Bladder Cancer (per 1,000) (95% Upper Confidence Limit) | |
| in Water, ppb | Males | Females |
| 10 | 0.0028 | 0.0086 |
| (0.314) | (0.094) | |
| 25 | 0.0172 | 0.0540 |
| (0.787) | (0.253) | |
| 50 | 0.0690 | 0.2161 |
| (1.580) | (0.564) | |
multistage Weibull model was fitted to the data grouped by exposure intervals of 300 ppb (resulting groups 0-300 ppb, > 300-600 ppb, and > 600 ppb), 275 ppb (resulting groups 0-275 ppb, > 275-550 ppb, and > 550 ppb), 250 ppb (resulting groups 0-250 ppb, > 250-500 ppb, > 500-750 ppb, and > 750 ppb), 150 ppb (resulting groups 0-150 ppb, . . . > 600-750 ppb, and > 750 ppb), 100 ppb (resulting groups 0-100 ppb, . . .> 600-700 ppb, and > 700 ppb). The results for male bladder cancer are displayed graphically in Figures 10-4 and 10-5. Figure 10-4 shows fitted curves over the entire observable range of concentrations, and Figure 10-5 plots the curves only up to 100 ppb. The figures provide dramatic evidence of the effect that grouping can have on the estimated dose-response curve. The effect is especially noticeable at the lower end of the dose-response curve; that end of course, is of most interest. The figures suggest that the estimated risks at 50 ppb differ 30-fold across groupings. Table 10-9 lists the estimated risks at 10, 25, and 50 ppb under the various groupings displayed in the figures and confirms the impression gained from the figures. It is interesting also to see that there is no particular pattern
| TABLE 10-8 Sensitivity Analysis Based on Bladder Cancer in Males (Multistage Weibull Model) | |||
| Excess Lifetime Risk of Male Bladder Cancer (per 1,000) by Arsenic Concentration | |||
| Village Exclusion Criteria | 10 ppb | 25 ppb | 50 ppb |
| Single well | 0.0024 | 0.0153 | 0.0612 |
| Multiple wells | 0.0037 | 0.0229 | 0.0914 |
| Highest five villages | 0.0021 | 0.0130 | 0.0519 |
| Lowest five villages | 0.3244 | 0.8142 | 1.6386 |
Page 283
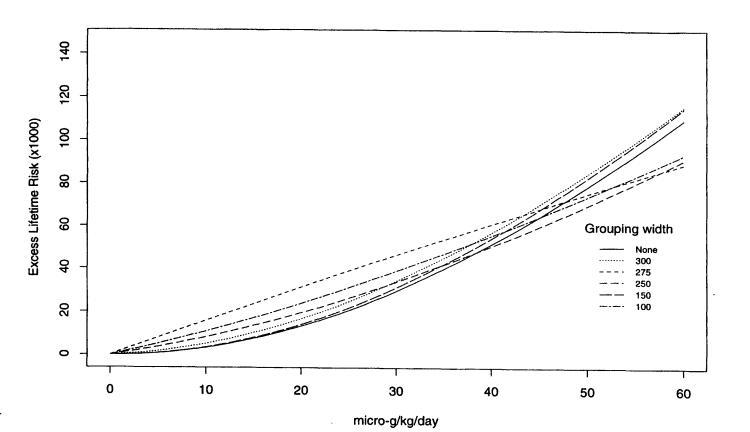
Figure 10-4
Dose response for bladder cancer in males. Excess lifetime risks per 1,000 people estimated under different
degrees of grouping of arsenic concentrations.
Page 284
| TABLE 10-9 Excess Lifetime Risk Estimates with Different Groupings of Arsenic Exposure Concentrations | |||
| Excess Lifetime Risk of Male Bladder Cancer (per 1,000) by Arsenic Concentration | |||
| Group | 10 ppb | 25 ppb | 50 ppb |
| None | 0.0028 | 0.0172 | 0.0690 |
| 300 | 0.0593 | 0.1581 | 0.3494 |
| 275 | 0.4597 | 1.1485 | 2.2948 |
| 250 | 0.1928 | 0.4870 | 0.9902 |
| 150 | 0.0029 | 0.0182 | 0.0727 |
| 100 | 0.2815 | 0.07072 | 1.4256 |
with respect to the degree of grouping. For example, the results under "no grouping" are not particularly close to the results obtained by grouping into the smallest grouping category of 100 ppb. As discussed earlier in the chapter, the Berkson measurement-error theory would predict grouping to have only a relatively minor influence on the fitted curves if the correct mean concentrations were assigned to each group. Thus, the fact that grouping does have a strong effect provides evidence of additional measurement error in the arsenic concentrations being assigned at the village level.
Other Issues
To address the possibility that some of the model sensitivity to grouping and village deletions might be due to the multistage Weibull model, we explored alternatives based on Poisson regression modeling techniques. Such explorations should be part of any data-analysis exercise and are especially important in the risk-assessment setting where low-dose estimates are well known to be sensitive to model choice. The simplest Poisson modeling approach characterizes the log of the cancer death rate as a linear function of covariates. Nonlinear and interaction effects can easily be explored in the context by considering additional appropriate covariates (Breslow and Day 1988). By modeling on the log scale, such models implicitly assume a multiplicative effect of exposure. Additive models may also be explored, although they are not as easy to fit using standard statistical software. The model assumes that the number of cancer deaths among subjects exposed to a specified concentration in a particular age group follows a Poisson distribution with rate equal to the cancer death rate, multiplied by the person-years at
Page 285
| TABLE 10-9 Excess Lifetime Risk Estimates with Different Groupings of Arsenic Exposure Concentrations | |||
| Excess Lifetime Risk of Male Bladder Cancer (per 1,000) by Arsenic Concentration | |||
| Group | 10 ppb | 25 ppb | 50 ppb |
| None | 0.0028 | 0.0172 | 0.0690 |
| 300 | 0.0593 | 0.1581 | 0.3494 |
| 275 | 0.4597 | 1.1485 | 2.2948 |
| 250 | 0.1928 | 0.4870 | 0.9902 |
| 150 | 0.0029 | 0.0182 | 0.0727 |
| 100 | 0.2815 | 0.07072 | 1.4256 |
with respect to the degree of grouping. For example, the results under "no grouping" are not particularly close to the results obtained by grouping into the smallest grouping category of 100 ppb. As discussed earlier in the chapter, the Berkson measurement-error theory would predict grouping to have only a relatively minor influence on the fitted curves if the correct mean concentrations were assigned to each group. Thus, the fact that grouping does have a strong effect provides evidence of additional measurement error in the arsenic concentrations being assigned at the village level.
Other Issues
To address the possibility that some of the model sensitivity to grouping and village deletions might be due to the multistage Weibull model, we explored alternatives based on Poisson regression modeling techniques. Such explorations should be part of any data-analysis exercise and are especially important in the risk-assessment setting where low-dose estimates are well known to be sensitive to model choice. The simplest Poisson modeling approach characterizes the log of the cancer death rate as a linear function of covariates. Nonlinear and interaction effects can easily be explored in the context by considering additional appropriate covariates (Breslow and Day 1988). By modeling on the log scale, such models implicitly assume a multiplicative effect of exposure. Additive models may also be explored, although they are not as easy to fit using standard statistical software. The model assumes that the number of cancer deaths among subjects exposed to a specified concentration in a particular age group follows a Poisson distribution with rate equal to the cancer death rate, multiplied by the person-years at risk in that age group. Several alternatives were considered, including log-linear models that were linear or quadratic in dose and age, along with interactions.
Page 286
Figure 10-6 shows the excess lifetime risk estimates under the following fitted models: (1) linear in dose and age, (2) quadratic in dose and age, and (3) quadratic in age and linear in dose. The fourth curve, which incorporates background data, will be discussed presently. According to Akaike's information criteria, the best fitting of models 1 -3 was the one with a quadratic age and a linear dose effect, although the improvement in fit over the model that was only linear in dose and age was relatively minor at low doses (see Figure 10-6). Interactions did not improve the model fit. Under the model that was quadratic in age and linear in dose, the estimated lifetime risks per 1,000 people at 10, 25, and 50 ppb were 0.206, 0.518, and 1.049, respectively. The corresponding upper confidence limits were 0.264, 0.665, and 1.347, respectively. Because standard maximum-likelihood theory is straightforward to apply for the Poisson model, confidence limits were based on analytical calculations rather than bootstraps.
Another important issue to address is whether and how to incorporate information about an unexposed population. It could be argued that cancer data from the whole of Taiwan should be used as a comparison unexposed population. The advantage of using such data is that more information is available to estimate the shape of the dose-response curve at low exposure concentrations. Another advantage is that the fitted curves might be slightly more robust to miss-specification of the exposure concentrations in the individual villages. The disadvantage is that data from Taiwan as a whole might not be a suitable comparison group because of differences in lifestyle. Also, the Taiwanese-wide data do not clearly represent a population with zero exposure to arsenic in drinking water. Because good arguments can be made for both sides, the subcommittee felt that it was important to explore the effect of including such baseline data. Table 10-10 shows the data used from Taiwan. There are several approaches to incorporating such baseline data. One approach is to fit exactly the same kinds of models described above but with the data from the whole of Taiwan as additional person-years and cancer data corresponding to zero exposure. Notice in Figure 10-6 that the fitted curves that include the Taiwanese-wide data are somewhat different from those obtained using only data from the endemic region. What seems to happen is that the ''zero" point is now estimated with so much precision that the curve changes at low dose, being in fact slightly more sublinear in shape. Table 10-11 summarizes the estimated risks (per 1,000) at 10, 25, and 50 ppb based on Poisson regression models, with and without the baseline data included. Note that, consistent with Figure 10-6, the estimated risks are lower under the model that incorporates baseline data.
Another way to incorporate comparison data, such as those presented in Table 10-10, is through the use of standardized mortality ratios (SMRs), (see
Page 287
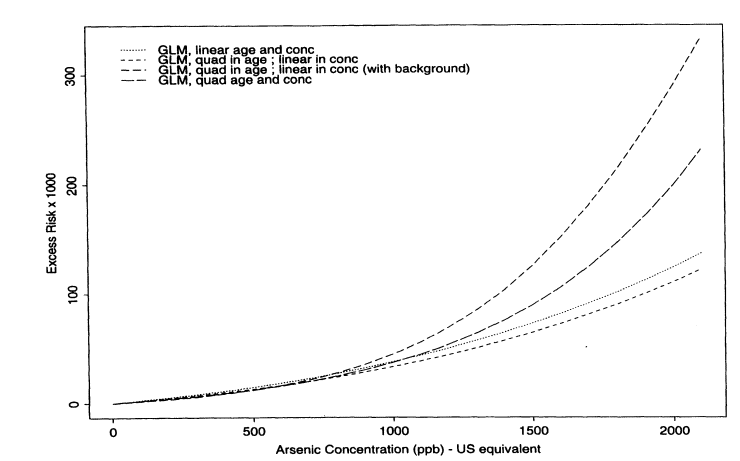
FIGURE 10-6
Estimated excess lifetime risks of bladder-cancer per 1,000 males based on Poisson regression models.
Page 288
| Table 10-10 Taiwanese-Wide Data on Bladder Cancer | ||
| Age Group | Population | Bladder Cancers, No. |
| Male | ||
| 20-25 | 13,271,386 | 0 |
| 25-30 | 11,054,191 | 3 |
| 30-35 | 8,628,516 | 4 |
| 35-40 | 6,793,545 | 8 |
| 40-45 | 6,375,466 | 20 |
| 45-50 | 6,384,052 | 50 |
| 50-55 | 6,062,515 | 91 |
| 55-60 | 5,018,542 | 164 |
| 60-65 | 3,666,535 | 213 |
| 65-70 | 2,443,367 | 345 |
| 70-75 | 1,480,126 | 413 |
| 75-80 | 720,375 | 418 |
| 80+ | 392,714 | 305 |
| Female | ||
| 20-25 | 13,266,327 | 0 |
| 25-30 | 11,054,808 | 0 |
| 30-35 | 8,210,507 | 2 |
| 35-40 | 6,458,620 | 2 |
| 40-45 | 5,802,856 | 5 |
| 45-50 | 5,157,821 | 20 |
| 50-55 | 4,365,755 | 41 |
| 55-60 | 3,517,193 | 76 |
| 60-65 | 2,776,622 | 124 |
| 65-70 | 2,106,715 | 153 |
| 70-75 | 1,490,659 | 173 |
| 75-80 | 888,468 | 185 |
| 80+ | 650,835 | 157 |
Note that, consistent with Figure 10-6, the estimated risks are lower under the model that incorporates baseline data.
Another way to incorporate comparison data, such as those presented in Table 10-10, is through the use of standardized mortality ratios (SMRs), (see
Breslow and Day 1988, for an excellent discussion). The basic idea in an SMR analysis is to use a large population based on a comparison group to calculate the expected numbers of cancer deaths within different age categories of the study population. SMRs are widely used by epidemiologists to characterize the excess risk in an exposed population, relative to an appropriate comparison group. Several of the studies reported in Chapter 4 are based on the SMR approach. Smith and Sharp (1985), Wright et al. (1997), and others have also argued that SMRs can be used as the basis for quantitative risk assessment. Indeed, several recent EPA risk assessments (e.g., on butadiene) have been based on this approach.
The subcommittee briefly illustrates how the SMR approach works by considering again the male bladder-cancer data. The first step is to calculate the expected number of cancers within each age group for each village. For
Page 289
example, in village "2-M," there are 1,057 person-years at risk among males aged 40-45. Based on the Taiwanese-wide data in Table 10-10, the expected number of cancers is 1,057*20/6,375,466 = 0.0033, compared with 0 actually observed in that group. Similarly, for 690 person-years at risk among males aged 50-55 in the same village, we expect 690*91/6,062,515 = 0.0104 cancer deaths compared with 2 actually observed. A useful summary statistic for each village can be obtained by summing over all the age groups to get a total expected number. The ratio of observed to expected then gives a village a specific SMR. For village "2-M," for example, these calculations yield an expected number of 0.18 cancer deaths, compared with 9 actually observed. Taking the ratio of those numbers yields an SMR of 50, although the estimates are fairly unstable because of the low expected numbers. As with the analyses described previously, Poisson regression can be again used to characterize the dose response. This time, however, observed numbers of cancer deaths in each age and concentration combination are modeled as following a Poisson distribution with rate parameter R*l, where R is the expected number. The parameter l reflects the relative risk and can be modeled as a function of concentration and any other covariates available. It is also possible to allow age to affect l as well. For example, it might be that the relative risk is higher among older people (see Breslow and Day 1988, section 4.6). In fact, the best-fitting model was one that had age and concentration as linear terms. Once a model has been fitted in this way, then lifetime risks can be calculated using the formulas given in Equations 5 and 6, except that pq(x, t) is now estimated by using the baseline cancer risks taken from the U.S. population combined with the relative-risk model estimated in the Taiwanese population. For example, that approach yields estimated risks at 10, 25, and 50 ppb of 0.1802, 0.4537 and 0.9181 per 1,000, respectively. The corresponding upper 95 % confidence limits are 0.2227, 0.5608, and 1.135428 per 1,000.
Finally, we turn to some discussion of how the new EPA guidelines (EPA 1996) might apply in the present setting. If biological considerations suggest the presence of a nonlinear dose response, then the new guidelines would suggest specifying an appropriate model and using it to estimate low-dose risks. For example, the Poisson model could be used, in which case the model-based estimates in Table 10-11 might be adopted as the estimated risks at 10, 25, and 50 ppb. In the absence of a convincing biological argument for the use of a nonlinear model to predict risks at low doses, EPA generally recommends the use of a point-of-departure approach (EPA 1996). Basically, the idea is to estimate the dose corresponding to a low risk that is still high enough for the corresponding dose to be within the observable range of data. Risks at lower doses can be estimated by linear extrapolation from the point of departure. In the absence of mechanistic data to support linear extrapolation, however, EPA
Page 290
| Table 10-11 Excess Lifetime Risk Estimates for Bladder Cancer in Malesa | |||
| Excess Lifetime Risk of Male Bladder Cancer (per 1,000) (95% Upper Confidence Limit) | |||
| Arsenic Concentration | |||
| in Water, ppb | No Baseline Dataa | With Baseline Dataa | SMR Approachb |
| 10 | 0.206 (0.264) | 0.140 (0.155) | 0.179 (0.222) |
| 25 | 0.518 (0.665) | 0.356 (0.393) | 0.450 (0.559) |
| 50 | 1.049 (1.347) | 0.731 (0.807) | 0.911 (1.132) |
| aModels are quadratic in age and linear in concentration. | |||
| bModel is linear in age and concentration. | |||
recommends calculating a "margin of exposure," which is the ratio of the dose at the point of departure to doses of environmental concern. The point-of-departure approach is similar in spirit to the benchmark-dose approach (see Crump 1984), which has become popular in noncancer risk assessment. As discussed in the EPA 1996 guidelines, a 10% level of risk is often chosen as the point of departure. (That is about the risk level that can be detected with reasonable power in an animal bioassay.) For risk assessments based on epidemiological data, however, a lower point of departure is often warranted because the observable range of effects can go lower in epidemiological studies than animal studies where the numbers are often small. In the case of the bladder-cancer data, a 10% excess lifetime risk is about the level seen at the very highest concentrations of exposure. Hence, it is more reasonable to select a 5 % or a 1% excess risk level as the point of departure. Table 10-12 shows the estimated doses corresponding to a 1% point of departure, along with lower 95% confidence limits. The margin of exposure and the excess risk level at 50 ppb, based on linear extrapolation from the point of departure, are also shown. Three approaches are considered: (1) Poisson modeling without including background data from the whole of Taiwan; (2) Poisson modeling with background data included as part of the data set being modeled; and (3) Poisson modeling using the SMR approach. It is interesting to see from the table that those approaches are fairly consistent at the 1% risk level, although some of them yielded considerably different estimators at very low doses, particularly with respect to the estimated risks at 50 ppb (see Table 10-11). This consistency occurs because the point-of-departure approach does not require extrapolation outside the range where data are directly observable, and it is one of the attractive features of the point-of-departure approach.
Discussion
This chapter has reviewed some of the sources of uncertainty associated with the 1988 EPA arsenic risk assessment, which was based on the skin-cancer
Page 291
| Table 10-12 Estimated Points of Departure at the 1% Excess Risk Level, Corresponding Margin of Exposure at 50 ppb, and Corresponding Excess Lifetime Risk Estimates at 50 ppb for Bladder Cancer in Malesa | |||
| Point of | Margin of Exposure | Risk at 50 ppb | |
| Method of Analysis | Departure, ppb | at 50 ppb | (x 1,000) |
| Poisson model, | 404 | 8.08 | 1.237 |
| No background data | (323) | (6.46) | (1.548) |
| Poisson model, | 443 | 8.86 | 1.129 |
| Background data included | (407) | (8.14) | (1.229) |
| Poisson model, | 450 | 9.0 | 1.111 |
| SMR approach | (372) | (7.44) | (1.344) |
| aFigures in parentheses are 95% confidence limits (lower for the point-of-departure estimates, upper for estimated risk at 50 ppb). | |||
data from the Tseng study. One serious problem was the study's ecological design: exposure concentrations were not individually measured; instead, individuals were assigned to one of three broad exposure groups (high, medium, and low), according to the mean exposure concentration found in their village. Assigning the average exposure concentration from a group to all individuals within the same group can result in what is known as the Berkson measurement-error model. It is well known that regression models fitted to data subject to the Berkson measurement-error model are unlikely to have serious bias, although variability might be underestimated. However, that result only holds if the exposure concentrations measured at the group level are not themselves subject to measurement error. According to the theory, the exposure concentration assigned to each group should reflect the mean exposure concentration of all subjects within the group. In the case of the Tseng data, it is impossible to know whether the representative values assigned to the high-, medium-, and low-exposure categories were appropriate. To assess the possible effects of choosing the wrong representative values for the three exposure categories, the analysis was redone using different values. The estimated excess lifetime risk at 50 ppb was found to range from about 1 to 5 per 1,000 people, with corresponding upper confidence limits of 3.2 to 7.1. Those results suggest that, although problems exist in using the Tseng data, the conclusions to be drawn about estimated exposure effects are not likely to change too drastically, although the level of uncertainty increases quite a lot because of the issues of grouping and measurement error.
This chapter has presented exploratory analyses of some bladder-cancer mortality data from the arsenic endemic region of Taiwan, the focus being primarily on bladder cancer in males. Although these data are ecological, they have some advantages over Tseng's skin-cancer data. First, the age breakdown was more reliable, because the data were extracted from age-specific mortality
Page 292
data. Second, arsenic concentrations were available for each of 42 separate villages and were not simply classified as low, medium, and high. Thus, the new data were perhaps less contaminated by problems of measurement error, although it is still a serious concern and could persist at the village level. In particular, arsenic concentrations detected in multiple wells varied considerably within some of the villages, leading to uncertainty about the exposure concnetrations assigned to each village. Regardless of that uncertainty, the availability of village-specific exposure measurements provided a useful opportunity to assess directly the effects of grouping exposure into high, medium, and low categories, as was done in the Tseng study. Figure 10-5 showed the results of fitting the multistage Weibull model to the bladder-cancer data in males, with various amounts of grouping artificially imposed. The results show that for these data, grouping can have a fairly strong effect on the fitted model.
The chapter has also reported on the issue of model fit. Several approaches were taken to address that concern. First, to see whether individual villages could have a significant impact on the fitted multistage Weibull model, sensitivity analyses were run, refitting the model with certain villages excluded from the analysis. For instance, the 20 villages with only one well measured for arsenic were excluded. Exclusions were also made of the villages with more than one well measured, the five villages with the highest measurements, and the five with the lowest measurements. As seen in Table 10-8, the resulting estimates of the excess lifetime risk of cancer can change fairly substantially by several orders of magnitude.
Those sensitivity analyses were useful and suggested that the fit of the multistage Weibull model was indeed sensitive to the subset of villages chosen for analysis. As an alternative, we explored Poisson regression models, which were found to fit as well as, if not better than, the multistage Weibull model. The basic approach was to include age and exposure terms as possibly linear and quadratic effects on the cancer incidence rate. Although a quadratic effect in age improved the fit, a linear effect for exposure seemed to be adequate. Interactions did not improve the model fit. The Poisson modeling yielded estimated risks that were higher than those based on the multistage Weibull model. For example, the estimated risk at 50 ppb was 1.049 per 1,000, with an upper confidence limit of 1.347 per 1,000, or almost 1 excess cancer per 1,000 population.
Several alternative ways to incorporate external information on age-specific cancer death rates were explored, including methods based on SMRs and Poisson regression models. By providing more information about baseline risks, those approaches can lead to more precise estimates of the dose response (Breslow and Day 1988, p. 151). A disadvantage, however, is the potential for bias if the comparison population is not well chosen. Also, it is difficult to
Page 293
determine whether the comparison population can be considered to have zero exposure. The analyses presented in this chapter used age-specific cancer rates reported for the whole of Taiwan. Bias could be a potential problem, because the Taiwanese-wide data might not form an appropriate comparison group for the arsenic endemic region, which is a poor, rural area. Thus, the choice to use external information on baseline cancer rates represents a tradeoff that to some extent can be explored using sensitivity analysis.
This chapter has focused primarily on issues related to the analysis and dose-response modeling of the data from Taiwan. In addition to the modeling issues already discussed, extrapolating the results to the U.S. population raises some additional sources of uncertainty. For example, differences between the United States and Taiwan with respect to the amount of arsenic in food could affect the relevance of the results.
It should be noted that ecological studies in Chile (Smith et al. 1998) and Argentina (Hopenhayn-Rich et al. 1996, 1998) have observed risks of lung and bladder cancer of the same magnitude as those reported in the studies in Taiwan at comparable levels of exposure. As presented in Chapter 4, in both the high-exposure regions in Chile and Argentina, the excess numbers of male lung-cancer deaths was in a range of 4 to 5 times that of the excess number of bladder-cancer deaths. Risk estimates for Taiwan have also been reported to be greater for lung cancer than bladder cancer (Smith et al. 1992). Among males, the contribution to risk from lung cancer based on Taiwan data (5.3 per 1,000) (see Table 4-5) was well over twice the bladder-cancer risk (2.3 per 1,000) for estimates for consumption of water with a concentration of 50 µg/L. In view of the analyses discussed in this chapter indicating that the risk for bladder cancer in males at the current maximum contaminant level (MCL) might be 1.0 to 1.5 per 1,000, a similar approach for all cancers in both sexes could easily result in a combined cancer risk on the order of 1 in 100.
The analyses presented in this chapter are based primarily on what is sometimes called a statistical approach to risk assessment. An argument can be made that the multistage Weibull model is derived for biological considerations; however, the philosophy behind statistical modeling is simply to describe the data using a flexible class of dose-response models that can accommodate a wide variety of shapes. In recent years, there has been a lot of interest in the development and application of more biologically based models that account for intake, metabolic pathways, and mode of action; in practice, the approach is rarely used because usually not enough is known about the mode of action for the compound in question. Arsenic certainly falls into that category. Use of biomarkers in the construction of dose-response models is a related idea that has generated a lot of interest in recent years. In practice, however, the data are generally not available to use that approach. Furthermore, statistical methods to incorporate biomarkers into dose-response models
Page 294
have not been developed. Research to develop such approaches would be extremely valuable.
Summary and Conclusions
The statistical issues surrounding risk assessment for arsenic in drinking water are challenging. The lack of reliable animal data means that risk assessment needs to be based solely on epidemiological data. However, the best available data are from ecological studies, which are not ideal for risk-assessment purposes (NRC 1991). Thus, even though issues of interspecies extrapolation are avoided through the use of human data, issues of confounding and measurement error have the potential to bias the results. This chapter has reviewed a number of issues:
1. The limitations of risk assessment based on ecological data.
2. The effects of measurement error induced by the use of ecological data, grouping of exposure concentrations, or both.
3. The impact of model choice; in particular, comparison of estimates based on the multistage Weibull model and other classes of dose-response models.
4. The appropriate ways to adjust for age in risk assessments based on epidemiological data and to incorporate baseline data on expected cancer rates among unexposed subjects.
Based on the subcommittee's findings, a number of general comments can be made. First, there is no question that the ideal basis for risk assessment is a well-conducted epidemiological study involving accurate assessment of individual exposures. In the absence of such data, however, ecological data might be the only choice. Such analyses must be conducted with caution, keeping in mind the potential for measurement error and confounding to bias the results. It is important to remember that any risk assessment based on ecological data must be cautiously interpreted because of the inherent uncertainty in the exposure-assessment methods used for such studies. In the case of the Taiwanese data, the fact that it came from a culturally homogeneous area provides some reassurance that confounding might not be too serious a concern. Our findings also suggest that additional caution might be needed when exposure concentrations are grouped into broad exposure categories. It is important to keep in mind that the considerable variability in the arsenic concentrations detected in multiple wells within some of the villages leads to considerable uncertainty about exposure concentrations in the Taiwanese data.
Page 295
The subcommittee's explorations suggest that model choice can have a major impact on estimated low-dose risks when the analysis is based on epidemiological data. The impact of model choice is amplified in that setting, because the model must also account for the effect of age. We began by considering the multistage Weibull model, because it was used by EPA in its 1988 evaluation of the skin-cancer data. As an alternative, we considered Poisson regression models, with age and exposure allowed to enter the model with linear and quadratic terms as well as interaction terms. We found that a Poisson model with a quadratic term in age and a linear term in exposure fitted the data well (using likelihood-based criteria) and yielded estimated lowdose risks that were substantially higher than those based on the multistage Weibull model. It is important to note that "exposure" in our models referred to concentration of arsenic in the drinking water. A good argument could also be made for using cumulative exposure instead. Although interaction terms did not improve our model (suggesting that concentration in the drinking water might be an appropriate basis for modeling), further exploration of this issue is needed.
The subcommittee also explored analyses that incorporated data on Taiwanese-wide cancer rates. One approach simply included the Taiwanese-wide data as additional data for the Poisson regression analysis. A second approach was based on SMRs, which can also be analyzed using Poisson regression but replacing person-years at risk with the expected numbers of cancer deaths, estimated using the baseline comparison population. Because there are advantages and disadvantages of all the approaches discussed here, the subcommittee repeated the analysis using several feasible assumptions before drawing conclusions. In the case of bladder cancer in males, the Poisson regression analyses yielded fairly consistent results, regardless of whether baseline data were incorporated into the analysis.
As an alternative to model-based estimates of risk at low doses, the subcommittee explored methods based on the point-of-departure methods discussed in the 1996 draft EPA guidelines for carcinogen risk assessment. As expected, we found that using this method gave much more consistent low-dose risk estimates across a wide range of dose-response models. Indeed, the estimated points of departure for male bladder cancer were all around 400 ppb (± 50 ppb), which yields a margin of exposure of only 8 with respect to the current MCL.
Finally, some factors should be noted that might affect assessment of risk in Taiwan or extrapolation to the United States but could not be taken into account quantitatively in this chapter. These factors include poor nutrition and low selenium concentrations in Taiwan, genetic and cultural characteristics, and arsenic intake from food.
Page 296
Recommendations
Ideally, risk assessment for arsenic in drinking water would be based on a well-designed and well-executed epidemiological study involving individual exposure assessment. In the absence of such a study, however, ecological data might be the only choice. Although such data can provide a basis for risk assessment, it is important to keep in mind the potential for bias due to confounding and measurement error. Therefore, the subcommittee recommends that several analyses be conducted to assess the sensitivity of the results to model choice, particular subsets of data, and the way that exposure concentrations are grouped together.
Although the subcommittee has not tried to perform a definitive risk assessment, it has used data on bladder-cancer rates for the 42 villages in the arsenic endemic region of Taiwan to illustrate statistical issues that arise in this context. For the actual risk assessment, the subcommittee recommends conducting analyses based on bladder, lung, and other internal cancers. Specifically, separate analyses should be conducted for each of those cancers, as well as for the combined end point corresponding to those three cancer types.
Model selection can be particularly important in settings where one needs to account for both age and dose effects. The subcommittee found that the multistage Weibull model was sensitive to omitting various subsets of villages, as well as to the way that exposure was grouped. Although not presented in this chapter, limited sensitivity analyses suggest that generalized linear models (GLMs) might be more robust. In particular, the male bladder-cancer data seemed to be well described by a GLM that included a linear dose and quadratic age effect, although we did not explore additive models. Models based on SMRs could also be used and might be advantageous in the context of being less sensitive to how age is characterized in the modeling process. The SMR approach can also provide added precision by incorporating external information on baseline cancer death rates. However, care is needed in choosing an appropriate comparison population. Regardless of the data set that is ultimately used for the arsenic risk assessment, the subcommittee recommends that a range of feasible modeling approaches be explored. The final calculated risk should be supported by a range of analyses over a fairly broad feasible range of assumptions. Performing a sensitivity analysis ensures that the conclusions do not rely heavily on any one particular assumption.
References
Breslow N.E., and N.E. Day. 1988. Statistical Methods in Cancer Research:
Page 297
The Design and Analysis of Cohort Studies, Vol. 2. Oxford, U.K.: Oxford University Press.
Brown, K.G., H.R. Guo, T.L. Kuo, and H.L. Greene. 1997. Skin cancer and inorganic arsenic: Uncertainty status of risk. Risk Anal. 17:37-42.
Carroll, R.J., and L.A. Stefanski. 1990. Approximate quasi-likelihood estimation in models with surrogate predictors. J. Am. Stat. Assoc. 85:652-663.
Carroll R.J., D. Rappert, and L.A. Stefanski. 1995. Measurement Error in Nonlinear Models. New York: Chapman & Hall. 336 pp.
Chen, C.J., T.L. Kuo, and M.M. Wu. 1988. Arsenic and cancers [letter]. Lancet i:414-415.
Chen, C.J., C.W. Chen, M.M. Wu, and T.L. Kuo. 1992. Cancer potential in liver, lung, bladder and kidney due to ingested inorganic arsenic in drinking water. Br. J. Cancer 66:888-892.
Cox, D.R., and D. Oakes. 1984. Analysis of Survival Data. New York: Chapman & Hall.
Crump, K.S. 1984. A new method for determining allowable daily intakes. Fundam. Appl. Toxicol. 4:854-871.
Efron, B., and R.J. Tibshirani. 1993. An Introduction to the Bootstrap. New York: Chapman & Hall.
EPA (U.S. Environmental Protection Agency). 1988. Special Report on Inorganic Arsenic: Skin Cancer; Nutritional Essentiality. EPA 625/387/013. U.S. Environmental Protection Agency, Risk Assessment Forum, Washington, D.C.
EPA (U.S. Environmental Protection Agency). 1996. Proposed guidelines for carcinogen risk assessment. Notice. Fed. Regist. 61(79):1795918011.
Gart, J.J., D. Krewski, P.N. Lee, R.E. Tarone, and J. Wahrendorf. 1986. Statistical Methods in Cancer Research. Vol. 3: The Design and Analysis of Long-Term Animal Experiments, J. Wahrendorf, ed. Oxford, U.K.: Oxford University Press.
Geyer, C.J. 1991. Constrained maximum likelihood exemplified by isotonic convex logistic regression. J. Am. Stat. Assoc. 86:717-724.
Greenland, S., and H. Morgenstern. 1989. Ecological bias, confounding and effect modification. Int. J. Epidemiol. 18:269-274.
Greenland, S. and J. Robins. 1994. Invited commentary: Ecologic studiesbiases, misconceptions, and counter-examples. Am. J. Epidemiol. 139:747-760.
Guess, H. A., and K.S. Crump. 1978. Maximum likelihood estimation of dose-response functions subject to absolutely monotonic constraints. Ann. Stat. 6:101-111.
Holland, C.D., and R.L. Sielken, Jr. 1993. Quantitative Cancer Modeling and Risk Assessment. Englewood Cliffs, N.J.: Prentice-Hall.
Page 298
Hopenhayn-Rich, C., M.L. Biggs, A. Fuchs, R. Bergoglio, E.E. Tello, H. Nicolli, and A.H. Smith. 1996. Bladder cancer mortality associated with arsenic in drinking water in Argentina. Epidemiology 7:117-124.
Hopenhayn-Rich C., M.L. Biggs, and A.H. Smith. 1998. Lung and kidney cancer mortality associated with arsenic in drinking water in Córdoba, Argentina. Int. J. Epidemiol. 27:561-569.
Laird, N., and D. Olivier. 1981. Covariance analysis of censored survival data using log-linear analysis techniques. J. Am. Stat. Assoc. 76:231-240.
NCHS (National Center for Health Statistics). 1998. Vital Statistics of the United States, 1994, Preprint, Vol. 2, Mortality, Pt. A, Sec. 6 Life Tables. National Center for Health Statistics, Hyattsville, Md.
NRC (National Research Council). 1991. Environmental Epidemiology. Washington, D.C.: National Academy Press.
Prentice, R.L., and L. Sheppard. 1995. Aggregate data studies of disease risk factors. Biometrika 82:113-125.
Self, S.G., and K.Y. Liang. 1987. Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J. Am. Stat. Assoc. 82:605-610.
Smith, A.H., and D.S. Sharp. 1985. A standardized benchmark approach to the use of cancer epidemiology data for risk assessment. Toxicol. Ind. Health 1:205-212.
Smith, A.H., C. Hopenhayn-Rich, M.N. Bates, H.M. Goeden, I. HertzPicciotto, H. Duggan, R. Wood, M. Kosnett, and M.T. Smith. 1992. Cancer risks from arsenic in drinking water. Environ. Health Perspect. 97:259-67.
Smith, A.H., M. Goycolea, R. Haque, and M.L. Biggs. 1998. Marked increase in bladder and lung cancer mortality in a region of northern Chile due to arsenic in drinking water. Am. J. Epidemiol. 147:660-669.
Tseng, W.P., H.M. Chu, and S.W. How. 1968. Prevalence of skin cancer in an endemic area of chronic arsenicism in Taiwan. J. Natl. Cancer Inst. 40:453-463.
Wright, C., P. Lopipero, and A.H. Smith. 1997. Meta analysis and risk assessment. Pp. 28-63 in Topics in Environmental Epidemiology, K. Steenland and D.A. Savitz, eds. New York: Oxford University Press.
Wu, M.M., T.L. Kuo, Y.H. Hwang, and C.J. Chen. 1989. Dose-response relation between arsenic concentration in well water and mortality from cancers and vascular diseases. Am. J. Epidemiol. 130:1123-1232.



































