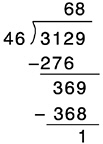6
DEVELOPING PROFICIENCY WITH WHOLE NUMBERS
Whole numbers are the easiest numbers to understand and use. As we described in the previous chapter, most children learn to count at a young age and understand many of the principles of number on which counting is based. Even if children begin school with an unusually limited facility with number, intensive instructional activities can be designed to help them reach similar levels as their peers.1 Children’s facility with counting provides a basis for them to solve simple addition, subtraction, multiplication, and division problems with whole numbers. Although there still is much for them to work out during the first few years of school, children begin with substantial knowledge on which they can build.
In this chapter, we examine the development of proficiency with whole numbers. We show that students move from methods of solving numerical problems that are intuitive, concrete, and based on modeling the problem situation directly to methods that are more problem independent, mathematically sophisticated, and reliant on standard symbolic notation. Some form of this progression is seen in each operation for both single-digit and multidigit numbers.
We focus on computation with whole numbers because learning to compute can provide young children the opportunity to work through many number concepts and to integrate the five strands of mathematical proficiency. This learning can provide the foundation for their later mathematical development. Computation with whole numbers occupies much of the curriculum in the early grades, and appropriate learning experiences in these grades improve children’s chances for later success.
Whole number computation also provides an instructive example of how routine-appearing procedural skills can be intertwined with the other strands of proficiency to increase the fluency with which the skills are used. For years, learning to compute has been viewed as a matter of following the teacher’s directions and practicing until speedy execution is achieved. Changes in career demands and the tasks of daily life, as well as the availability of new computing tools, mean that more is now demanded from the study of computation. More than just a means to produce answers, computation is increasingly seen as a window on the deep structure of the number system. Fortunately, research is demonstrating that both skilled performance and conceptual understanding are generated by the same kinds of activities. No tradeoffs are needed. As we detail below, the activities that provide this powerful result are those that integrate the strands of proficiency.
Operations with Single-Digit Whole Numbers
As students begin school, much of their number activity is designed to help them become proficient with single-digit arithmetic. By single-digit arithmetic, we mean the sums and products of single-digit numbers and their companion differences and quotients (e.g., 5+7=12, 12–5=7, 12–7=5 and 5×7=35, 35÷5=7, 35÷7=5). For most of a century, learning single-digit arithmetic has been characterized in the United States as “learning basic facts,” and the emphasis has been on memorizing those facts. We use the term basic number combinations to emphasize that the knowledge is relational and need not be memorized mechanically. Adults and “expert” children use a variety of strategies, including automatic or semiautomatic rules and reasoning processes to efficiently produce the basic number combinations.2 Relational knowledge, such as knowledge of commutativity, not only promotes learning the basic number combinations but also may underlie or affect the mental representation of this basic knowledge.3
The domain of early number, including children’s initial learning of single-digit arithmetic, is undoubtedly the most thoroughly investigated area of school mathematics. A large body of research now exists about how children in many countries actually learn single-digit operations with whole numbers. Although some educators once believed that children memorize their “basic facts” as conditioned responses, research shows that children do not move from knowing nothing about the sums and differences of numbers to having the basic number combinations memorized. Instead, they move through a series of progressively more advanced and abstract methods for working out the answers
to simple arithmetic problems. Furthermore, as children get older, they use the procedures more and more efficiently.4 Recent evidence indicates children can use such procedures quite quickly.5 Not all children follow the same path, but all children develop some intermediate and temporary procedures.
Most children continue to use those procedures occasionally and for some computations. Recall eventually becomes the predominant method for some children, but current research methods cannot adequately distinguish between answers produced by recall and those generated by fast (nonrecall) procedures. This chapter describes the complex processes by which children learn to compute with whole numbers. Because the research on whole numbers reveals how much can be understood about children’s mathematical development through sustained and interdisciplinary inquiry, we give more details in this chapter than in subsequent chapters.
Word Problems: A Meaningful Context
One of the most meaningful contexts in which young children begin to develop proficiency with whole numbers is provided by so-called word problems. This assertion probably comes as a surprise to many, especially mathematics teachers in middle and secondary school whose students have special difficulties with such problems. But extensive research shows that if children can count, they can begin to use their counting skills to solve simple word problems. Furthermore, they can advance those counting skills as they solve more problems.6 In fact, it is in solving word problems that young children have opportunities to display their most advanced levels of counting performance and to build a repertoire of procedures for computation.
Most children entering school can count to solve word problems that involve adding, subtracting, multiplying, and dividing.7 Their performance increases if the problems are phrased simply, use small numbers, and are accompanied by physical counters for the children to use. The exact procedures children are likely to use have been well documented. Consider the following problems:
Sally had 6 toy cars. She gave 4 to Bill. How many did she have left?
Sally had 4 toy cars. How many more does she need to have 6?
Most young children solve the first problem by counting a set of 6, removing 4, and counting the remaining cars to find the answer. In contrast,
they solve the second problem by counting a set of 4, adding in more as they count “five, six,” and then counting those added in to find the answer.
Children solve these problems by “acting out” the situation—that is, by modeling it. They invent a procedure that mirrors the actions or relationships described in the problem. This simple but powerful approach keeps procedural fluency closely connected to conceptual understanding and strategic competence. Children initially solve only those problems that they understand, that they can represent or model using physical objects, and that involve numbers within their counting range. Although this approach limits the kinds of problems with which children are successful, it also enables them to solve a remarkable range of problems, including those that involve multiplying and dividing.
Since children intuitively solve word problems by modeling the actions and relations described in them, it is important to distinguish among the different types of problems that can be represented by adding or subtracting, and among those represented by multiplying or dividing. One useful way of classifying problems is to heed the children’s approach and examine the actions and relations described. This examination produces a taxonomy of problem types distinguished by the solution method children use and provides a framework to explain the relative difficulty of problems.
Four basic classes of addition and subtraction problems can be identified: problems involving (a) joining, (b) separating, (c) part-part-whole relations, and (d) comparison relations. Problems within a class involve the same type of action or relation, but within each class several distinct types of problems can be identified depending on which quantity is the unknown (see Table 6–1). Students’ procedures for solving the entire array of addition and subtraction problems and the relative difficulty of the problems have been well documented.8
For multiplication and division, the simplest kinds of problems are grouping situations that involve three components: the number of sets, the number in each set, and the total number. For example:
Jose made 4 piles of marbles with 3 marbles in each pile. How many marbles did Jose have?
In this problem, the number and size of the sets is known and the total is unknown. There are two types of corresponding division situations depending on whether one must find the number of sets or the number in each set. For example:
Table 6–1
Addition and Subtraction Problem Types
|
Problem Type |
|
||
|
Join |
(Result Unknown) |
(Change Unknown) |
(Start Unknown) |
|
|
Connie had 5 marbles. Juan gave her 8 more marbles. How many marbles does Connie have altogether? |
Connie has 5 marbles. How many more marbles does she need to have 13 marbles altogether? |
Connie had some marbles. Juan gave her 5 more. Now she has 13 marbles. How many marbles did Connie have to start with? |
|
Separate |
(Result Unknown) |
(Change Unknown) |
(Start Unknown) |
|
|
Connie had 13 marbles. She gave 5 to Juan. How many marbles does Connie have left? |
Connie had 13 marbles. She gave some to Juan. Now she has 5 marbles left. How many marbles did Connie give to Juan? |
Connie had some marbles. She gave 5 to Juan. Now she has 8 marbles left. How many marbles did Connie have to start with? |
|
Part- Part- |
(Whole Unknown) |
|
(Part Unknown) |
|
Whole |
Connie has 5 red marbles and 8 blue marbles. How many marbles does she have altogether? |
|
Connie has 13 marbles: 5 are red and the rest are blue. How many blue marbles does Connie have? |
|
Compare |
(Difference Unknown) |
(Compare Quantity Unknown) |
(Referent Unknown) |
|
|
Connie has 13 marbles. Juan has 5 marbles. How many more marbles does Connie have than Juan? |
Juan has 5 marbles. Connie has 8 more than Juan. How many marbles does Connie have? |
Connie has 13 marbles. She has 5 more marbles than Juan. How many marbles does Juan have? |
|
SOURCE: Carpenter, Fennema, Franke, Levi, and Empson, 1999, p. 12. Used by permission of Heinemann. All rights reserved. |
|||
Jose has 12 marbles and puts them into piles of 3. How many piles does he have?
Jose has 12 marbles and divides them equally into 3 piles. How many marbles are in each pile?
Additional types of multiplication and division problems are introduced later in the curriculum. These include rate problems, multiplicative comparison problems, array and area problems, and Cartesian products.9
As with addition and subtraction problems, children initially solve multiplication and division problems by modeling directly the action and relations in the problems.10 For the above multiplication problem with marbles, they form four piles with three in each and count the total to find the answer. For the first division problem, they make groups of the specified size of three and count the number of groups to find the answer. For the other problem, they make the three groups by dealing out (as in cards) and count the number in one of the groups. Although adults may recognize both problems as 12 divided by 3, children initially think of them in terms of the actions or relations portrayed. Over time, these direct modeling procedures are replaced by more efficient methods based on counting, repeated adding or subtracting, or deriving an answer from a known number combination.11
The observation that children use different methods to solve problems that describe different situations has important implications. On the one hand, directly modeling the action in the problem is a highly sensible approach. On the other hand, as numbers in problems get larger, it becomes inefficient to carry out direct modeling procedures that involve counting all of the objects.
Children’s proficiency gradually develops in two significant directions. One is from having a different solution method for each type of problem to developing a single general method that can be used for classes of problems with a similar mathematical structure. Another direction is toward more efficient calculation procedures. Direct-modeling procedures evolve into the more advanced counting procedures described in the next section. For word problems, these procedures are essentially abstractions of direct modeling that continue to reflect the actions and relations in the problems.
The method children might use to solve a class of problems is not necessarily the method traditionally taught. For example, many children come to solve the “subtraction” problems described above by counting, adding up, or thinking of a related addition combination because any of these methods is easier and more accurate than counting backwards. The method traditionally presented in textbooks, however, is to solve both of these problems by
subtracting, which moves students toward the more difficult and error-prone procedure of counting down. Ultimately, most children begin to use recall or a rapid mental procedure to solve these problems, and they come to recognize that the same general method can be used to solve a variety of problems.
Single-Digit Addition
Children come to understand the meaning of addition in the context of word problems. As we noted in the previous section, children move from counting to more general methods to solve different classes of problems. As they do, they also develop greater fluency with each specific method. We call these specific counting methods procedures. Although educators have long recognized that children use a variety of procedures to solve single-digit addition problems,12 substantial research from all over the world now indicates that children move through a progression of different procedures to find the sum of single-digit numbers.13
This progression is depicted in Box 6–1. First, children count out objects for the first addend, count out objects for the second addend, and count all of the objects (count all). This general counting-all procedure then becomes abbreviated, internalized, and abstracted as children become more experienced with it. Next, they notice that they do not have to count the objects for the first addend but can start with the number in the first or the larger addend and count on the objects in the other addend (count on). As children count
|
Box 6–1 Learning Progression for Single-Digit Addition  |
on with objects, they begin to use the counting words themselves as countable objects and keep track of how many words have been counted on by using fingers or auditory patterns. The counting list has become a representational tool. With time, children recompose numbers into other numbers (4 is recomposed into 3+1) and use thinking strategies in which they turn an addition combination they do not know into one they do know (3+4 becomes 3+3+1). In the United States, these strategies for derived number combinations often use a so-called double (2+2, 3+3, etc.). These doubles are learned very quickly.
As Box 6–1 shows, throughout this learning progression, specific sums move into the category of being rapidly recalled rather than solved in one of the other ways described above. Children vary in the sums they first recall readily, though doubles, adding one (the sum is the next counting word), and small totals are the most readily recalled. Several procedures for single-digit addition typically coexist for several years; they are used for different numbers and in different problem situations. Experience with figuring out the answer to addition problems provides the basis both for understanding what it means to say “5+3=8” and for eventually recalling that sum without the use of any conscious strategy.
Children in many countries often follow this progression of procedures, a natural progression of embedding and abbreviating. Some of these procedures can be taught, which accelerates their use,14 although direct teaching of these strategies must be done conceptually rather than simply by using imitation and repetition.15 In some countries, children learn a general procedure known as “make a 10” (see Box 6–2).16 In this procedure the solver makes a 10 out of one addend by taking a number from the other addend. Educators in some countries that use this approach believe this first instance of regrouping by making a 10 provides a crucial foundation for later multidigit arithmetic. In some Asian countries this procedure is presumably facilitated by the number words.17 It has also been taught in some European countries in which the number names are more similar to those of English, suggesting that the procedure can be used with a variety of number-naming systems. The procedure is now beginning to appear in U.S. textbooks,18 although so little space may be devoted to it that some children may not have adequate time and opportunity to understand and learn it well.
There is notable variation in the procedures children use to solve simple addition problems.19 Confronted with that variation, teachers can take various steps to support children’s movement toward more advanced procedures. One technique is to talk about slightly more advanced procedures and why
|
Box 6–2 Make a Ten: B+6=?  |
they work.20 The teacher can stimulate class discussion about the procedures that various students are using. Students can be given opportunities to present their procedures and discuss them. Others can then be encouraged to try the procedure. Drawings or concrete materials can be used to reveal how the procedures work. The advantages and disadvantages of different procedures can also be examined. For a particular procedure, problems can be created for which it might work well or for which it is inefficient.
Other techniques that encourage students to use more efficient procedures are using large numbers in problems so that inefficient counting procedures cannot easily be used and hiding one of the sets to stimulate a new way of thinking about the problem. Intervention studies indicate that teaching counting-on procedures in a conceptual way makes all single-digit sums accessible to U.S. first graders, including children who are learning disabled and those who do not speak English as their first language.21 Providing support for children to improve their own procedures does not mean, however, that every child is taught to use all the procedures that other children develop. Nor does it mean that the teacher needs to provide every child in a class with
support and justification for different procedures. Rather, the research provides evidence that, at any one time, most children use a small number of procedures and that teachers can learn to identify them and help children learn procedures that are conceptually more efficient (such as counting on from the larger addend rather than counting all).22
Mathematical proficiency with respect to single-digit addition encompasses not only the fluent performance of the operation but also conceptual understanding and the ability to identify and accurately represent situations in which addition is required. Providing word problems as contexts for adding and discussing the advantages and disadvantages of different addition procedures are ways of facilitating students’ adaptive reasoning and improving their understanding of addition processes.
Single-Digit Subtraction
Subtraction follows a progression that generally parallels that for addition (see Box 6–3). Some U.S. children also invent counting-down methods that model the taking away of numbers by counting back from the total. But counting down and counting backward are difficult for many children.23
|
Box 6–3 Learning Progression for Single-Digit Subtraction  |
A considerable number of children invent counting-up procedures for situations in which an unknown quantity is added to a known quantity.24 Many of these children later count up in taking-away subtraction situations (13–8=? becomes 8+?=13). When counting up is not introduced, many children may not invent it until the second or third grade, if at all. Intervention studies with U.S. first graders that helped them see subtraction situations as taking away the first x objects enabled them to learn and understand counting-up-to procedures for subtraction. Their subtraction accuracy became as high as that for addition.25
Experiences that focus on part-part-whole relations have also been shown to help students develop more efficient thinking strategies, especially for subtraction.26 Students examine a join or separate situation and identify which number represents the whole quantity and which numbers represent the parts. These experiences help students see how addition and subtraction are related and help them recognize when to add and when to subtract. For students in grades K to 2, learning to see the part-whole relations in addition and subtraction situations is one of their most important accomplishments in arithmetic.27
For students in grades K to 2, learning to see the part-whole relations in addition and subtraction situations is one of their most important accomplish-ments in arithmetic.
Examining the relationships between addition and subtraction and seeing subtraction as involving a known and an unknown addend are examples of adaptive reasoning. By providing experiences for young students to develop adaptive reasoning in addition and subtraction situations, teachers are also anticipating algebra as students begin to appreciate the inverse relationships between the two operations.28
Single-Digit Multiplication
Much less research is available on single-digit multiplication and division than on single-digit addition and subtraction. U.S. children progress through a sequence of multiplication procedures that are somewhat similar to those for addition.29 They make equal groups and count them all. They learn skip-count lists for different multipliers (e.g., they count 4, 8, 12, 16, 20,…to multiply by four). They then count on and count down these lists using their fingers to keep track of different products. They invent thinking strategies in which they derive related products from products they know.
As with addition and subtraction, children invent many of the procedures they use for multiplication. They find patterns and use skip counting (e.g., multiplying 4×3 by counting “3, 6, 9, 12”). Finding and using patterns and other thinking strategies greatly simplifies the task of learning multiplication tables (see Box 6–4 for some examples).30 Moreover, finding and describing
|
Box 6–4 Thinking Strategies for Single-Digit Multiplication In single-digit arithmetic, there are 100 multiplication combinations that students must learn. Commutativity reduces that number by about half. Multiplication by 0 and by 1 may quickly be deduced from the meaning of multiplication. Multiplication by 2 consists of the “doubles” from addition. Single-digit multiplication by 9 is simplified by a pattern: in the product, the sum of the digits is 9. (For example, 9×7=63 and 6+3=9.) Multiplication by 5 may also be deduced through patterns or by first multiplying by 10 and then dividing by 2, since 5 is half of 10. The remaining 15 multiplication combinations (and their commutative counterparts) may be computed by skip counting or by building on known combinations. For example, 3×6 must be 6 more than 2×6, which is 12. So 3×6 is 18. Similarly, 4×7 must be twice 2×7, which is 14. So 4×7 is 28. (Note that these strategies require proficiency with addition.) To compute multiples of 6, one can build on the multiples of 5. So, for example, 6×8 must be 8 more than 5×8, which is 40. So 6×8 is 48. If students are comfortable with such strategies for multiplication by 3, 4, and 6, only three multiplication combinations remain: 7×7, 7×8, and 8×8. These can be derived from known combinations in many creative ways. |
patterns are a hallmark of mathematics. Thus, treating multiplication learning as pattern finding both simplifies the task and uses a core mathematical idea.
After children identify patterns, they still need much experience to produce skip-count lists and individual products rapidly. Little is known about how children acquire this fluency or what experiences might be of most help. A good deal of research remains to be done, in the United States and in other countries, to understand more about this process.
Single-Digit Division
Division arises from the two splitting situations described above. A collection is split into groups of a specified size or into a specified number of groups. Just as subtraction can be thought of using a part-part-whole relation, division can be thought of as splitting a number into two factors. Hence, divisions can also be approached as finding a missing factor in multiplication. For example, 72÷9=? can be thought of as 9÷?=72. But there is little
research concerning how best to introduce and use this relationship, or whether it is helpful to learn a division combination at the same time as the corresponding multiplication combination. Further, there is little research about how to help children learn and use easily all of the different symbols for division, such as ![]() 15÷3, and
15÷3, and ![]()
Practicing Single-Digit Calculations
Practicing single-digit calculations is essential for developing fluency with them. This practice can occur in many different contexts, including solving word problems.31 Drill alone does not develop mastery of single-digit combinations.32 Practice that follows substantial initial experiences that support understanding and emphasize “thinking strategies” has been shown to improve student achievement with single-digit calculations.33 This approach allows computation and understanding to develop together and facilitate each other. Explaining how procedures work and examining their benefits, as part of instruction, support retention and yield higher levels of performance.34 In this way, computation practice remains integrated with the other strands of proficiency such as strategic competence and adaptive reasoning.
Practicing single-digit calculations is essential for developing fluency with them.
It is helpful for some practice to be targeted at recent learning. After students discuss a new procedure, they can benefit from practicing it. For example, if they have just discussed the make-a-10 procedure (see Box 6–2), solving problems involving 8 or 9 in which the procedure can easily be used provides beneficial practice. It also is helpful for some practice to be cumulative, occurring well after initial learning and reviewing the more advanced procedures that have been learned.
Many U.S. students have had the experience of taking a timed test that might be a page of mixed addition, subtraction, multiplication, and division problems. This scattershot form of practice is, in our opinion, rarely the best use of practice time. Early in learning it can be discouraging for students who have learned only primitive, inefficient procedures. The experience can adversely affect students’ disposition toward mathematics, especially if the tests are used to compare their performance.35 If appropriately delayed, timed tests can benefit some students, but targeted forms of practice, with particular combinations that have yet to be mastered or on which efficient procedures can be used, are usually more effective.36
Summary of Findings an Learning Single-Digit Arithmetic
For addition and subtraction, there is a well-documented progression of procedures used worldwide37 by many children that stems from the sequential nature of the list of number words. This list is first used as a counting tool; then it becomes a representational tool in which the number words themselves are the objects that are counted.38 Counting becomes abbreviated and rapid, and students begin to develop procedures that take advantage of properties of arithmetic to simplify computation. During this progression, individual children use a range of different procedures on different problems and even on the same problem encountered at different times.39 Even adults have been found to use a range of different procedures for simple addition problems.40 Further, it takes an extended period of time before new and better strategies replace previously used strategies.41 Learning-disabled children and others having difficulty with mathematics do not use procedures that differ from this progression. They are just slower than others in moving through it.42
Instruction can help students progress.43 Counting on is accessible to first graders; it makes possible the rapid and accurate addition of all single-digit numbers. Single-digit subtraction is usually more difficult than addition for U.S. children. If children understand the relationship between addition and subtraction, perhaps by thinking of the problem in terms of part-part-whole, then they recognize that counting up can be used to solve subtraction problems. This recognition makes subtraction more accessible.44
The procedures of counting on for addition and counting up for subtraction can be learned with relative ease. Multiplication and division are somewhat more difficult. Even adults might not have quick ways of reconstructing the answers to problems like 6×8=? or ![]() if they have forgotten the answers. Learning these combinations seems to require much specific pattern-based knowledge that needs to be orchestrated into accessible and rapid-enough products and quotients. As with addition and subtraction, children derive some multiplication and division combinations from others; for example, they recall that 6×6=36 and use that combination to conclude that 6×7=42. Research into ways to support such pattern finding, along with the necessary follow-up thinking and practice, is needed if all U.S. children are to acquire higher levels of proficiency in single-digit arithmetic.
if they have forgotten the answers. Learning these combinations seems to require much specific pattern-based knowledge that needs to be orchestrated into accessible and rapid-enough products and quotients. As with addition and subtraction, children derive some multiplication and division combinations from others; for example, they recall that 6×6=36 and use that combination to conclude that 6×7=42. Research into ways to support such pattern finding, along with the necessary follow-up thinking and practice, is needed if all U.S. children are to acquire higher levels of proficiency in single-digit arithmetic.
Acquiring proficiency with single-digit computations involves much more than rote memorization. This domain of number demonstrates how the different strands of proficiency contribute to each other. At this early point in
development, many of the linkages among strands result from children’s natural inclination to make sense of things and to engage in actions that they understand. Children begin with conceptual understanding of number and the meanings of the operations. They develop increasingly sophisticated representations of the operations such as counting-on or counting-up procedures as they gain greater fluency. They also lean heavily on reasoning to use known answers such as doubles to generate unknown answers. Even in the early grades, students choose adaptively among different procedures and methods depending on the numbers involved or the context.45 As long as the focus in the classroom is on sense making, they rarely make nonsensical errors, such as adding to find the answer when they should subtract. Proficiency comes from making progress within each strand and building connections among the strands. A productive disposition is generated by and supports this kind of learning because students recognize their competence at making sense of quantitative situations and solving arithmetic problems.
Multidigit Whole Number Calculations
Step-by-step procedures for adding, subtracting, multiplying, or dividing numbers are called algorithms. For example, the first step in one algorithm for multiplying a three-digit number by a two-digit number is to write the three-digit number above the two-digit number and to begin by multiplying the one’s digit in the top number by the one’s digit in the bottom number (see Box 6–5).
In the past, algorithms different from those taught today for addition, subtraction, multiplication, and division have been taught in U.S. schools. Also, algorithms different from those taught in the United States today are currently being taught in other countries.46 Each algorithm has advantages
|
Box 6–5 Beginning a multiplication algorithm |
and disadvantages. Therefore, it is important to think about which algorithms are taught and the reasons for teaching them.
Learning to use algorithms for computation with multidigit numbers is an important part of developing proficiency with numbers. Algorithms are procedures that can be executed in the same way to solve a variety of problems arising from different situations and involving different numbers. This feature has three important implications. First, it means that algorithms are useful tools—different procedures do not need to be invented for each problem. Second, algorithms illustrate a significant feature of mathematics: The structure of problems can be abstracted from their immediate context and compared to see whether different-looking problems can be solved in similar ways. Finally, the process of developing fluency with arithmetic algorithms in elementary school can contribute to progress in developing the other strands of proficiency if time is spent examining why algorithms work and comparing their advantages and disadvantages. Such analyses can boost conceptual understanding by revealing much about the structure of the number system itself and can facilitate understanding of place-value representations.
Research findings about learning algorithms for whole numbers can be summarized with seven important observations. First, the linkages among the strands of mathematical proficiency that are possible when children develop proficiency with single-digit arithmetic can be continued with multidigit arithmetic. For example, there can be a close connection between understanding and fluency. Conceptual knowledge that comes with understanding is important for the development of procedural fluency, while fluent procedural knowledge supports the development of further understanding and learning. When students fail to grasp the concepts that underlie procedures or cannot connect the concepts to the procedures, they frequently generate flawed procedures that result in systematic patterns of errors.47 These so-called buggy algorithms are signs that the strands are not well connected.48 When the initial computational procedures that students use to solve multidigit problems reflect their understanding of numbers, understanding and fluency develop together.
A second observation is that understanding and fluency are related. For multidigit addition and subtraction, given conventional instruction that emphasizes practicing procedures, a substantial percentage of children gain understanding of multidigit concepts before using a correct procedure, but another substantial minority do the opposite.49 In contrast, instructional programs that emphasize understanding algorithms before using them have been shown to lead to increases in both conceptual and procedural knowledge.50
So there is some evidence that understanding is the basis for developing procedural fluency.51
A third observation is that proficiency with multidigit computation is more heavily influenced by instruction than single-digit computation is. Many features of multidigit procedures (e.g., the base-10 elements and how they are represented by place-value notation) are not part of children’s everyday experience and need to be learned in the classroom. In fact, many students are likely to need help learning efficient forms of multidigit procedures. This means that students in different classrooms and receiving different instruction might follow different learning progressions use different procedures.52 For single-digit addition and subtraction, the same learning progression occurs for many children in many countries regardless of the nature and extent of instruction.53 But multidigit procedures, even those for addition and subtraction, depend much more on what is taught.
A fourth observation is that children can and do devise or invent algorithms for carrying out multidigit computations.54 Opportunities to construct their own procedures provide students with opportunities to make connections between the strands of proficiency. Procedural fluency is built directly on their understanding. The invention itself is a kind of problem solving, and they must use reasoning to justify their invented procedure. Students who have invented their own correct procedures also approach mathematics with confidence rather than fear and hesitation.55 Students invent many different computational procedures for solving problems with large numbers. For addition, they eventually develop a procedure that is consistent with the thinking that is used with standard algorithms. That thinking enables them to make sense of the algorithm as a record on paper of what they have already been thinking. For subtraction, many students can develop adding-up procedures and, if using concrete materials like base-10 blocks, can also develop ways of thinking that parallel algorithms usually taught today.56 Some students need help to develop efficient algorithms, however, especially for multiplication and division. Consequently, for these students the process of learning algorithms involves listening to someone else explain an algorithm and trying it out, all the while trying to make sense of it. Research suggests that students are capable of listening to their peers and to the teacher and of making sense of an algorithm if it is explained and if the students have diagrams or concrete materials that support their understanding of the quantities involved.57
Fifth, research has shown that students can learn well from a variety of different instructional approaches, including those that use physical materials to represent hundreds, tens, and ones, those that emphasize special counting
activities (e.g., count by tens beginning with any number), and those that focus on developing mental computation methods.58 Although the data do not point to a single preferred instructional approach, they do suggest that effective approaches share some key features: The multidigit procedures that students use are easily understood; students are encouraged to use algorithms that they understand; instructional supports (classroom discussions, physical materials, etc.) are available to focus students’ attention on the base-10 structure of the number system and on how that structure is used in the algorithm; and students are helped to progress to using reasonably efficient but still comprehensible algorithms.59
Sixth, research on symbolic learning argues that, to be helpful, manipulatives or other physical models used in teaching must be represented by a learner both as the objects that they are and as symbols that stand for something else.60 The physical characteristics of these materials can be initially distracting to children, and it takes time for them to develop mathematical meaning for any kind of physical model and to use it effectively. These findings suggest that sustained experience with any physical models that students are expected to use may be more effective than limited experience with a variety of different models.61
In view of the attention given to the use of concrete models in U.S. school mathematics classes, we offer a special note regarding their effective use in multidigit arithmetic. Research indicates that students’ experiences using physical models to represent hundreds, tens, and ones can be effective if the materials help them think about how to combine quantities and, eventually, how these processes connect with written procedures. The models, however, are not automatically meaningful for students; the meaning must be constructed as they work with the materials. Given time to develop meaning for a model and connect it with the written procedure, students have shown high levels of performance using the written procedure and the ability to give good explanations for how they got their answers.62 In order to support understanding, however, the physical models need to show tens to be collections of ten ones and to show hundreds to be simultaneously 10 tens and 100 ones. For example, base-10 blocks have that quality, but chips all of the same size but with different colors for hundreds, tens, and ones do not.
A seventh and final observation is that the English number words and the Hindu-Arabic base-10 place-value system for writing numbers complicate the teaching and learning of multidigit algorithms in much the same way, as discussed in Chapter 5, that they complicate the learning of early number concepts.63 Closely related to the difficulties posed by the irregu-
larities with number words are difficulties posed by the complexity of the system for writing numbers. As we said in chapter 3, the base-10 place-value system is very efficient. It allows one to write very large numbers using only 10 symbols, the digits 0 through 9. The same digit has a different meaning depending on its place in the numeral. Although this system is familiar and seems obvious to adults, its intricacies are not so obvious to children. These intricacies are important because research has shown that it is difficult to develop procedural fluency with multidigit arithmetic without an understanding of the base-10 system.64 If such understanding is missing, students make many different errors in multidigit computations.65
This conclusion does not imply that students must master place value before they can begin computing with multidigit numbers. In fact, the evidence shows that students can develop an understanding of both the base-10 system and computation procedures when they have opportunities to explore how and why the procedures work.66 That should not be surprising; it simply confirms the thesis of this report and the claim we made near the beginning of this chapter. Proficiency develops as the strands connect and interact.
The six observations can be illustrated and supported by examining briefly each of the arithmetic operations. As is the case for single-digit operations, research provides a more complete picture for addition and subtraction than for multiplication and division.
Addition Algorithms
The progression followed by students who construct their own procedures is similar in some ways to the progression that can be used to help students learn a standard algorithm with understanding. To illustrate the nature of these progressions, it is useful to examine some specific procedures in detail.
The episode in Box 6–6 from a third-grade class illustrates both how physical materials can support the development of thinking strategies about multidigit algorithms and one type of procedure commonly invented by children.67 The episode comes from a discussion of students’ solutions to a word problem involving the sum 54+48.
The episode suggests that students’ invented procedures can be constructed through progressive abstraction of their modeling strategies with blocks. First, the objects in the problem were represented directly with the blocks. Then, the quantity representing the first set was abstracted, and only the blocks representing the second set were counted. Finally, the counting words were themselves counted by keeping track of the counts on fingers.
|
Box 6–6 A Third-Grade Class Finds 54+48 The students had worked on the problem at their desks for about 15 minutes and were sharing their procedures with the class. The teacher, Ms. G., called everyone over to look at Ellen’s solution strategy.
SOURCE: Adapted from Carpenter, Fennema, and Franke, 1996, p. 11. |
Ellen’s final solution was for all intents and purposes a verbal description of what she did with the blocks. But it was more than that. It represented a solution that could actually be carried out without the blocks as explicit referents. Other invented procedures share some of the same features.
Boxes 6–7 through 6–10 illustrate procedures for multidigit addition and subtraction. Method C in Box 6–7 captures, in written form, the thinking strategies that many students use as they continue constructing procedures for adding multidigit numbers.68 They usually begin by combining the larger units first and then combining the subtotals to find the sum. They invent a variety of mental and written techniques to keep track of the subtotals until they can combine them. The important observation is that students who construct these methods understand that ones are combined with ones, tens with tens, and hundreds with hundreds, and they understand that 10 of each unit compose one unit of the next higher magnitude (e.g., 10 tens make 100). Fundamental properties of the number system, like the associative and distributive properties, are used in decomposing and recombining numbers. In other words, the procedures children construct on their own build directly on the foundational number concepts, and these underlying concepts often are quite visible when one examines the steps in the procedures.
The procedures children construct on their own build directly on the foundational number concepts, and these underlying concepts often are quite visible when one examines the steps in the procedures.
Standard algorithms, in contrast to children’s constructed algorithms, are quite far removed from their conceptual underpinnings. They have evolved over centuries for efficiency and compactness. They can be executed quickly, but they can be difficult to learn with understanding.
Method A in Box 6–7 is an addition algorithm currently appearing in many U.S. textbooks. Learning this procedure with understanding poses three difficulties for many students. First, it moves from right to left, in contrast to reading and in contrast to most methods invented by children. Many children initially, and some children for a long time, have difficulty remembering to start on the right and move to the left.69 Second, for some children, putting the little 1’s above the top number changes the problem (it actually does change the problem, but that does not change the answer). This change can be a source of confusion. Third, adding the numbers in a given column is difficult with this method. You must add the 1 to the top number, remember the sum without writing it down, and add that remembered number you cannot see to the bottom number while you ignore the number you can see in the top row. If children instead add the two numbers they see (a much easier method), many of them then forget to add the extra 10 (or extra hundred).
|
Box 6–7 Three Methods for Muitidigit Addition A Common U.S. Algorithm 
Accessible Generalizable Methods 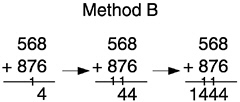

|
Method B is a variation of Method A that addresses two of these three problems (it also moves from right to left). Method B is taught in China and has been invented by students in the United States.70 In this method the new 1 or regrouped 10 (or new hundred) is recorded on the line separating the problem from the answer. This arrangement makes it easier to see the 14 that generated the regrouped 10 than when the 1 is written above the problem. Because the new 1 sits below in the answer space, it does not change the top number. Adding is easy: You just add the two numbers you see and then increase that total by one.
Methods A and B both require that children understand what to do when they get 10 or more in a given column. Because they can only write 9 or less of a given grouping in a column, they must make a group of 10 ones (or tens or hundreds, etc.) and give that group to the next left place. This conceptual trouble spot for students is called carrying or regrouping or trading. Method C, reflecting more closely many students’ invented procedures, reduces the problem by writing the total for each kind of unit on a new line. The carrying-regrouping-trading is done as part of the adding of each kind of unit. Also, Method C can be done in either direction (Box 6–7 shows the left-to-right version). Because you write out the whole value of each partial sum (e.g., 500 + 800 = 1300), this method also facilitates children’s thinking about and explaining how and what they are adding. Accessibility studies indicate that young children can solve multidigit addition problems using methods like B and C and some other methods also.71
Drawings like that in Box 6–8 can be used to support children’s understanding of the quantities in the problem and how those quantities are grouped to make new tens, hundreds, or thousands. Such drawings can be used with any of the three methods (or with other methods). Whether drawings or objects are used to support understanding of an addition method, it is vital that they be linked to the numbers in the algorithm until the student can perform it with understanding. If the drawings (or physical models like base-10 blocks) are used simply to calculate answers, they lose their ability to help connect understanding to procedures. The benefits of using the materials come from seeing that the actions performed on the drawings or objects to get answers are the very actions that are used in carrying out the algorithm. Learning the algorithm then becomes a matter of students recording with numbers on paper the actions and thinking they did with the drawings or objects. This linking process takes time. Asking students to explain their procedure as if the numbers were the drawings or physical models can facilitate the linking process.
|
Box 6–8 A Model for Multidigit Addition: 568+876=?  Stage 1: Sustained linking of quantities to written algorithm to quantity meanings. Stage 2: Only do algorithm but occasionally explain using quantity words. |
Subtraction Algorithms
Students can construct multidigit subtraction procedures, though often these procedures are less similar to standard algorithms than is the case for addition. Still, as with addition, research has shown that students can learn a subtraction algorithm meaningfully if provided with appropriate experiences. In most cases, subtraction algorithms require more time and support than addition algorithms, but students can learn to execute them accurately and to explain why they work.72
Two subtraction procedures are shown in Box 6–9. Method A is an algorithm commonly taught in the United States. It moves from right to left and alternates between the two major subtraction steps. Step 1 involves regrouping (or borrowing or trading) to get 10 or more in the top position. Step 2 is subtracting after the top number has been fixed. Alternating between these two steps presents three kinds of potential difficulties for students. The first is learning this alternation and the reasons for it. The second is remembering to alternate the steps. The third is that the alternation renders students susceptible to a very common subtracting error: subtracting a smaller top digit from a larger bottom digit. In the example, after subtracting bottom digit in
|
Box 6–9 Three Methods for Multidigit Subtraction A Common U.S. Algorithm 
Accessible Generalizable Methods  left-to-right ungrouping  right-to-left ungrouping Do all ungrouping, in any order, until every top number is larger than the bottom number. Then subtract each kind of multiunit, in any order. |
the ones place to get 6, a student moves to the left and sees 3 on the top and 6 on the bottom. The answer 3 is generated spontaneously as a subtraction answer, given 6 and 3. It takes extra effort to suppress this answer and think about the direction in which one is subtracting.
Methods B and C are slight variations of Method A in which Step 1 (regrouping) is done for all columns first. For each column in either direction, the student asks the regrouping (borrowing) question, “Can I subtract in this column? Is the top digit as big as or bigger than the bottom digit?”
|
Box 6–10 Model for Multidigit Subtraction: 1444–568=?  |
The goal is to fix the top number so that every top digit is larger than the corresponding bottom digit. The second major step is then to subtract in every column. This subtraction can also be done in any direction. Methods B and C clarify that the top number is a single number that must be rewritten in a form equivalent in value but ready for subtraction in every column. This rewriting can reduce the otherwise frequent “top from bottom” error.73
The drawing in Box 6–10 shows how students can make a quantity drawing to show both aspects of multidigit subtracting. Making such drawings initially can help students develop their own procedures or help them make sense of an algorithm presented by someone else. Again, such drawings should, when used, be linked to a numerical method and not just used to calculate an answer.
Multiplication Algorithms
There is much less research on children’s understanding of multidigit multiplication (and division) than of addition and subtraction. Sample conceptual teaching lessons have been published for multiplication, and some alternative methods of instruction have been explored.74 A preliminary learning progression of multidigit procedures that fosters children’s invention of
|
Box 6–11 A Common U.S. Algorithm for Multidigit Multiplication |
algorithms has also been reported.75 The data are still insufficient, however, to permit firm conclusions about students’ learning progressions in multidigit multiplication.
Nevertheless, it is useful to examine algorithms students are expected to learn and to consider alternatives that might facilitate understanding. Standard multiplication and division algorithms used in the United States are complex procedures in which multiplying alternates with adding or subtracting (see Box 6–11). In these algorithms the meaning and scaffolding provided by substeps have been sacrificed for efficiency. The algorithms use alignment of place value to keep the steps organized without requiring the student to understand what is actually happening with the ones, tens, hundreds, and so on. Algorithms that might be more accessible to students, and still generalizable and fairly efficient, are presented and discussed below.
Arrays are powerful representations of multiplication. An array or area model is shown on the left in Box 6–12. Such a model provides initial support for the crucial understanding of the effects of multiplying by 1, 10, and 100 (shown by arrows and products around the array). It also shows clearly how all of the tens and ones digits in 46 and 68 are multiplied by each other and then added. The sizes of the resulting rectangles indicate the sizes of these various products (sometimes referred to as partial products). The abbreviated array model (shown on the right in Box 6–12) can be drawn later when the students clearly understand the effects of multiplying by tens and by ones. This abbreviated model summarizes the steps in multidigit multiplication, and the separation into tens and ones facilitates finding the partial products.
|
Box 6–12 Models for Multidigit Multiplication: 46×68  |
The multiplication algorithm shown in Box 6–13 is an expanded form in which all possible products are written. As students come to understand each aspect of multiplication, some of the written supports can be dropped, resulting in a streamlined version that is a simple expanded form of typical U.S. algorithms. Although this algorithm has been proposed as an alternative for some time, and variations of it have been used in some textbooks,76 algorithms currently used in the United States are substantially different. They typically start at the right and multiply ones first. The expanded algorithm begins at the left, as students are naturally inclined to do. That also has the advantage that the first product written is the largest, which permits all of the smaller products to be aligned easily under it in their correct places. Writing the factors beside each product emphasizes what one is actually doing in each step and permits an easy check. In this variation the complex alternation of multiplying and adding is not necessary. Students who understand and wish
|
Box 6–13 Expanded Algorithm for Multidigit Multiplication  |
to drop steps in this algorithm can do so readily, with a result looking something like the common algorithm in Box 6–11, except that it has, in this case, four instead of two partial products to be added. These four can even be collapsed into two for those students who wish to do so. Therefore, the expanded model permits students to function at their own level of competence and is likely to help them understand what they are doing. The key point is that regardless of the algorithm that students use, they should be able to explain what they are doing and why it works.
Multiplying by a three-digit number is an extension of the two-digit version that requires the development of new understanding about multiplying by hundreds. The expanded algorithm for these larger numbers is relatively easy to carry out because the necessary steps are visible, although the number of partial products more than doubles. Given the accessibility of calculators, it might not be wise for students to spend a great deal of valuable school learning time becoming efficient at multiplication with three-digit or larger numbers. There is no research on how much pencil-and-paper computation is necessary or the impact of experiences with calculating with larger numbers on other mathematical understanding. Having some experience working with larger numbers, however, seems essential if students are to extend their conceptual understanding of multiplication and develop their ability to estimate
the results of calculating with large numbers. Both of these skills are important even when children use calculators.
At present, many students have not achieved procedural fluency with single-digit multiplication when they begin work on multidigit multiplication. A proper balance in instruction among the strands of mathematical proficiency would serve to diminish the number of such students. Until that balance is achieved, however, such students need help in working simultaneously on a multiplication algorithm and obtaining fluency with single-digit multiplication. Using a table to look up some single-digit products can permit students to participate in classwork on algorithms while perhaps motivating as well as supporting their continued learning of single-digit arithmetic.
Division Algorithms
As we indicated earlier, relatively little research is available to shed light on how students think about multidigit division or what learning activities might be of most help to them. Sample teaching lessons have been proposed, and preliminary results suggest that students can construct their own procedures that, over time, approximate standard algorithms.77 As with multiplication, however, the best that educators can do at this point is to examine some alternative algorithms that are likely to support students’ efforts to develop proficiency with multidigit division.
Common U.S. division algorithms have two aspects that can create difficulties for students. First, the algorithms require students to determine exactly the maximum copies of the divisor that can be taken from successive parts of the dividend. For example, in the problem 3129÷46=?, one must first determine exactly how many 46s can be subtracted from 312. That determination is not always easy. Second, the algorithms creates no sense of the size of the answers one is writing, in part because one is always multiplying by what looks like a single-digit number written above the dividend. In the example in Box 6–14, to begin the division process, the student just writes a 6 above the line as the first digit in the quotient. There is no sense of 60, because the student will be multiplying 46 by 6.
The accessible division method shown in Box 6–15 facilitates safe underestimating. Rather than trying to determine the largest number of 46s that can be subtracted from 312, the student can just keep subtracting multiples of 46s until the remainder is less than 46. This method builds experience with estimating (as well as accurate assessment of calculator answers) because students multiply by the correct number (e.g., 50, not 5). It is procedurally easy for those students still mastering multiplication combinations because it
|
Box 6–16 Expanded Algorithm for Multidigit Division with Fewer Steps  |
permits the use of products likely to be known. It can be made as brief as the current standard algorithm for those who can manage the abbreviation. This accessible division algorithm has been proposed as an alternative for some time and since at least the 1950s has been used in some textbooks.78
The example of the accessible method given in Box 6–15 shows a solution that might be produced by a student very early in learning division. Box 6–15 also gives a model that supports accessible methods. The student builds up copies of the divisor until the dividend is reached and then reads off the quotient. A later version of the procedure by the same student is given in Box 6–16. At this point the student no longer needs the drawing to give meaning to the steps. This version can readily be related to the more common method in Box 6–14.
Summary of Findings on Multidigit Calculations
Research indicates that U.S. children can understand and explain procedures for calculating with multidigit numbers rather than just executing them mechanically. This conclusion, which is especially well established for addition and subtraction,79 means that mathematical proficiency with multidigit arithmetic is achievable by students even at early grades. In fact, a higher level of performance can be achieved at earlier grades than is currently expected.80
Students acquire proficiency with multidigit algorithms by moving through a progression of experiences. Although there is relatively little research on students’ learning of multiplication and division algorithms, it is likely that their learning trajectories are similar to the ones documented for addition and subtraction. The progression might begin with problem modeling and the use of easily understood concrete representations and algorithms and move toward more efficient methods that are less transparent and more problem independent. Or it might begin by learning with understanding some method that easily makes sense when connected to the quantities involved. Some students invent their own methods for performing multidigit computations, and some learn by listening to others—another student or the teacher—explain a method. Whatever avenue students take, their procedural fluency is intertwined with their conceptual understanding and adaptive reasoning. The many kinds of errors students make when multidigit methods are not connected to place-value meanings are well documented.81
Research on addition and subtraction algorithms clearly indicates that helping students keep the strands of proficiency connected means providing supports for their efforts to make sense of written algorithms. The use of easily understood versions of algorithms can facilitate procedural fluency. Discussing and comparing different methods, including those that students bring from home, can provide opportunities to extend their understanding of place value and its uses. Teachers need to ensure that children who are less proficient have a relatively advanced method they understand and can use. The focus of instruction, however, should be on their understanding and explaining and not just on routine use. Comparing methods through classroom discussion is a means of facilitating reflection by all children on the conceptual and notational features of arithmetic algorithms.
Physical materials or drawings that show the different sizes of ones, tens, and hundreds can support the development of understanding if those supports are used to develop thinking strategies for combining quantities and if they are linked to written algorithms. What appears to be essential is that sufficient time and support are provided at the outset for children to develop meaning for the algorithms. That development hinges on certain prerequisite understanding (which may be developed alongside methods), and children also need to negotiate and become more skilled with the complexities of multistep, multidigit methods.82
How much of the precious time available for school mathematics should be spent on written algorithms with large numbers is a question that will need to be continually revisited during the twenty-first century. New goals
will arise to compete with the goal of fluency with written algorithms, as they already have. At present, it seems worthwhile to spend some time on written algorithms that facilitate students’ understanding of how multidigit procedures can be built from key concepts of place value and properties of the number system, such as the distributive property. Because calculating activities with large numbers incorporate calculations with single-digit numbers, such activities can also buttress children’s mastery of basic arithmetic. However, drilling for long periods on problems involving large numbers seems a goal more appropriate to the twentieth century than the twenty-first.
Mental Arithmetic and Estimation
Written procedures for adding, subtracting, multiplying, and dividing are the major focus of mathematics in the elementary school curriculum, and we have discussed how they can be integrated into the other strands of children’s developing mathematical proficiency. We end this chapter by considering two other kinds of calculation methods and the roles they can play in fostering the development of mathematical proficiency.
Mental Arithmetic
A number of researchers have argued that mental arithmetic—calculating the solution to multidigit arithmetic problems mentally without the use of pencil and paper—can lead to deeper insights into the number system.83 For example, a student might calculate 198×12 mentally by adding 2 to 198, multiplying 200 by 12 to get 2400, and then subtracting two 12s from the product, 2400–24=2376. Mental arithmetic, or mental math, can provide opportunities for students to practice and use numbers and operations in ways that promote making sense of the mathematics and reveal further insights into the properties of numbers and operations.
In the United States, mental calculation has not been emphasized in school mathematics in recent decades.
Beliefs about the contribution of mental arithmetic to the development of mathematical proficiency have changed over time and differ across countries. In nineteenth-century America, the ability to perform mental arithmetic was held in high esteem.84 Mental arithmetic, particularly as performed using a mental representation of the abacus, remains a popular activity in East Asian countries, with international competitions and a formalized system for rating calculation skill.85 In the United States, however, mental calculation has not been emphasized in school mathematics in recent decades.86
Mental arithmetic places a premium on flexible procedures that take advantage of mathematical structure and rely on well-known operations. Stu-
dents who have developed the ability to calculate mentally use a variety of procedures that take advantage of their knowledge of numbers, including working from left to right, using distributivity and other properties of arithmetic, and factoring numbers to simplify their work.87 These procedures can increase students’ awareness that typically there are multiple ways of solving any calculation problem.
Children entering school have already begun developing mental procedures for performing simple arithmetic, procedures that are eventually channeled into the pencil-and-paper algorithms that they can use for most computational work. If they are not encouraged to continue developing mental computation procedures, most will be inclined to view the new algorithms as the preferred, possibly the only, methods for computing and will discontinue use of mental procedures even when they are easier.88 There is evidence, though, that some instruction on mental arithmetic in upper elementary grades, if it is focused on understanding and uses number and operation properties, can move students away from the clumsy and error-prone mental use of written algorithms toward use of a variety of mental procedures better adapted to particular number combinations.89
Beyond its many practical uses in the modern world, mental arithmetic can promote mathematical proficiency by bringing together the various strands. Mental arithmetic should be taught to encourage children to reason about the problem situation and the numbers involved, to take advantage of their conceptual understanding of the properties and rules of arithmetic, and to strategically select and adapt procedures to simplify a computation and calculate the answer.
Estimation
Making estimates of exact answers is another form of computation that has its own special properties and uses in developing mathematical proficiency. Estimating before solving a problem can facilitate number sense and place-value understanding by encouraging students to use number and notational properties to generate an approximate result. Estimating is also a practical skill. It can guide students’ use of calculators, especially in identifying implausible answers, and is a valuable part of the mathematics used in everyday life.
Estimating the result of a computation is a complex skill in itself. It may require reformulating numbers, compensating for errors, and sometimes restructuring a problem.90 For example, the sum 261+242+235 could be
estimated by reformulating (in this case, rounding) each number as 250. In this form the simplest way of estimating the sum would be multiplying 250 by 3 and then compensating for the fact that the sum will be somewhat less than 750. Computational estimation takes advantage of important properties of numbers and notational systems, including powers often, place value, and relations among different operations. It also requires recognizing that the appropriateness of an estimate is related to the problem and its context.91 Estimation requires a flexibility of calculation that emphasizes adaptive reasoning and strategic competence, guided by children’s conceptual understanding of both the problem situation and the mathematics underlying the calculation.
Research on estimation shows how difficult it is for students who receive conventional instruction, with its frequent overemphasis on routine paper-and-pencil calculation, to move from calculating exact answers to estimating wisely. For example, one study92 reported that many students’ fear of being wrong led them to find the exact answer first and then round it to obtain a close estimate, with this tendency increasing from grades 5 to 9. Children also had difficulty using powers of 10 to identify the order of magnitude of a calculation (e.g., 4.638×87,325), and failed to understand that rounding can lead to systematic errors that need to be taken into account.
Estimating the results of a computation is a complex activity that should integrate all strands of mathematical proficiency. Its potential benefit is lost, however, if it is treated as a separate skill and taught as a set of isolated rules and techniques. Its benefit is realized when students are allowed to draw on other strands to find ways to simplify calculations and compensate for that simplification. For example, the representation students make of the mathematical situation enables them to make simple, appropriate estimates. Both fluency with computational procedures and awareness of the kinds of calculations that are easy to perform contribute to successful estimation. Finally, estimation is a good indicator of students’ productive disposition—in this case, their propensity to make sense of mathematical situations so that they understand that estimates are not wild guesses but informed, approximate solutions.
Developmental Themes
Becoming proficient with whole numbers is more complicated than many people realize. It is not simply moving quickly from ignorance to competence. Nor is it a matter of students following the teacher’s directions and explanations and then practicing until they get it right. Rather, it involves students—with support from learning materials, teachers, and peers—invent-
ing, understanding, and practicing methods; trying to learn and use concepts that look easy to adults but are challenging for children (e.g., place value); and gradually increasing their mathematical proficiency by continually seeking to make sense of number and numerical operations.
A few basic themes are critical. First, students’ progress viewed from a distance is marked by a kind of gradualness and continuity, but viewed up close it appears uneven and varied. At any given moment, students know and use a range of computation methods that may vary according to the numbers in the problem, the problem situation, and other individual and classroom variables. A student may use different methods even on very similar problems, and any new method competes for a long time with older methods and may not be used consistently. In general, however, students steadily extend methods they understand to solve a larger variety of problems, and they shape current methods into more efficient ones.
A second theme is the many ways in which the strands of proficiency can be interwoven. Initially, in classrooms focused on understanding, students’ conceptual understanding and procedural fluency are tightly connected— students use only methods they understand. Later, their learning in one strand boosts their progress in the others. As students become more fluent with multidigit algorithms, their understanding and use of the place-value notational system become more robust. As their reasoning about multidigit numbers and place-value concepts improves, they make sense of more efficient multidigit algorithms. Students also actively choose among different procedures and representations. In so doing, they strengthen their strategic knowledge and their conceptual understanding of the procedures and the representations. Not only is mathematical proficiency multidimensional, but also the path to proficient performance requires progress along each strand interactively.
A third and final theme is that there are some identifiable patterns in the development of students’ proficiency as long as the strands are allowed to develop together in mutual dependence. Students begin their study of number situations by modeling problems directly, using the context to shape their concrete and often cumbersome methods. They gradually move toward representing problems more abstractly. They apply methods that are less transparent and more embedded, abbreviated, and independent of the problem. These methods are more sophisticated mathematically, use structural properties such as commutativity, and use the place-value symbolic notation in productive ways. As students begin multidigit arithmetic, it is vital that teachers and classrooms provide support for all to build understanding of
multidigit quantities that can enable their calculation methods to become personally meaningful. Mathematical proficiency with whole numbers depends on all five strands developing together.
Notes
References
Ambrose, R., Baek, J., & Carpenter, T.P. (in press). Children’s construction of multiplication and division algorithms. In A.J.Baroody & A.Dowker (Eds.), The development of arithmetic concepts and skills: Constructing adaptive expertise. Mahwah, NJ: Erlbaum.
Armstrong, G.A. (1991). Use of the part-whole concept for teaching word problems to grade three children (Doctoral dissertation, National College of Education, 1990). Dissertation Abstracts International, 52(03), 833A.
Baek, J.-M. (1998). Children’s invented algorithms for multidigit multiplication problems. In L.J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 151–160). Reston, VA: NCTM.
Baroody, A.J. (1984a). Children’s difficulties in subtraction: Some causes and cures. Arithmetic Teacher, 32(3), 14–19.
Baroody, A.J. (1984b). The case of Felicia: A young child’s strategies for reducing memory demands during mental addition. Cognition and Instruction, 1, 109–116.
Baroody, A.J. (1985). Mastery of the basic number combinations: Internalization of relationships or facts? Journal of Research in Mathematics Education, 16, 83–98.
Baroody, A.J. (1987a). Children’s mathematical thinking: A developmental framework for preschool, primary, and special education teachers. New York: Teachers College Press.
Baroody, A.J. (1987b). The development of counting strategies for single-digit addition. Journal for Research in Mathematics Education, 18, 141–157.
Baroody, A.J. (1992). The development of kindergartners’ mental-addition strategies. Learning and Individual Differences, 4, 215–235.
Baroody, A.J. (1994). An evaluation of evidence supporting fact-retrieval models. Learning and Individual Differences, 6, 1–36.
Baroody, A.J. (1996). Self-invented addition strategies by children classified as mentally handicapped. American Journal of Mental Retardation, 101, 72–89.
Baroody, A.J. (1999a). Children’s relational knowledge of addition and subtraction. Cognition and Instruction, 17, 137–175.
Baroody, A.J. (1999b). The roles of estimation and the commutativity principle in the development of third-graders’ mental multiplication. Journal of Experimental Child Psychology, 74 [Special issue on mathematical cognition], 157–193.
Beberman, M. (1959). Introduction. In C.H.Shutter & R.L.Spreckelmeyer (Eds.), Teaching the third R. Washington, DC: Council for Basic Education.
Bednarz, N., & Janvier, B. (1982). The understanding of numeration in primary school. Educational Studies in Mathematics, 13, 33–57.
Beishuizen, M. (1993). Mental procedures and materials or models for addition and subtraction up to 100 in Dutch second grades. Journal for Research in Mathematics Education, 24, 294–323.
Beishuizen, M., Gravemeijer, K.P.E., & van Lieshout, E.C.D.M. (Eds.). (1997). The role of contexts and models in the development of mathematical strategies and procedures (pp. 163–198). Utrecht: CD-B Press/Freudenthal Institute.
Beishuizen, M., Van Putten, C.M., & Van Mulken, F. (1997). Mental arithmetic and strategy use with indirect number problems up to one hundred. Learning and Instruction, 7, 87–106.
Bergeron, J.C., & Herscovics, N. (1990). Psychological aspects of learning early arithmetic. In P.Nesher & J.Kilpatrick (Eds.), Mathematics and cognition: A research synthesis by the International Group for the Psychology of Mathematics Education. ICMI study series (pp. 31–52). Cambridge, UK: Cambridge University Press.
Bowers, J., Cobb, P., & McClain, K. (1999). The evolution of mathematical practices: A case study. Cognition and Instruction, 17, 25–64.
Bransford, J.D., Brown, A.L., & Cocking, R.R. (Eds.). (1999). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press. Available: http://books.nap.edu/catalog/6160.html. [July 10, 2001].
Brown, J.S., & Van Lehn, K. (1980). Repair theory: A generative theory of bugs in procedural skills. Cognitive Science, 4, 379–426.
Brownell, W.A. (1944). Rate accuracy and process in learning. Journal of Educational Psychology, 35, 321–337.
Brownell, W.A. (1987). AT classic: Meaning and skill—maintaining the balance. Arithmetic Teacher, 34(8), 18–25. (Original work published 1956)
Brownell, W.A., & Chazal, C.B. (1935). The effects of premature drill in third-grade arithmetic. Journal of Educational Research, 29, 17–28.
Buchanan, A.D. (1978). Estimation as an essential mathematical skill (Professional Paper No. 39, SWRL-PP-39). Los Alamitos, CA: Southwest Regional Laboratory for Educational Research and Development. (ERIC Document Reproduction Service No. ED 167 385)
Carnine, D.W., & Stein, M. (1981). Organizational strategies and practice procedures for teaching basic facts. Journal for Research in Mathematics Education, 12, 65–69.
Carpenter, T.P. (1985). Learning to add and subtract: An exercise in problem solving. In E.A.Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 17–40). Hillsdale, NJ: Erlbaum.
Carpenter, T.P., Ansell, E., Franke, M.L., Fennema, E., & Weisbeck, L. (1993). Models of problem solving: A study of kindergarten children’s problem-solving processes. Journal for Research in Mathematics Education, 24, 428–441.
Carpenter, T.P., Fennema, E., & Franke, M.L. (1996). Cognitively guided instruction: A knowledge base for reform in primary mathematics instruction. Elementary School Journal, 97, 3–20.
Carpenter, T.P., Fennema, E., Franke, M.L., Empson, S.B., & Levi, L.W. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Carpenter, T.P., Fennema, E., Peterson, P.L., Chiang, C.P., & Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26, 499–531.
Carpenter, T.P., Franke, M.L., Jacobs, V.R., Fennema, E., & Empson, S.B. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education, 29, 3–20.
Carpenter, T.P., & Moser, J.M. (1984). The acquisition of addition and subtraction concepts in grades one through three . Journal for Research in Mathematics Education, 15, 179–202.
Carpenter, T.P., Moser, M.J., & Romberg, T.A. (Eds.). (1982). Addition and subtraction: A cognitive perspective. Hillsdale, NJ: Erlbaum.
Carraher, T.N., Carraher, D.W., & Schliemann, A.D. (1987). Written and oral mathematics. Journal for Research in Mathematics Education, 18, 83–97.
Carroll, W.M., & Porter, D. (1997). Invented procedures can develop meaningful mathematical procedures. Teaching Children Mathematics, 3, 370–74.
Carroll, W.M., & Porter, D. (1998). Alternative algorithms for whole-number operations. In L.J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp.
106–114). Reston, VA: NCTM.
Cauley, K.M. (1988). Construction of logical knowledge: Study of borrowing in subtraction. Journal of Educational Psychology, 80, 202–205.
Cobb, P., & Bauersfeld, H. (Eds.). (1995). The emergence of mathematical thinking: Interaction in classroom cultures. Hillsdale, NJ: Erlbaum.
Cobb, P., & Wheatley, G. (1988). Children’s initial understandings of ten. Focus on Learning Problems in Mathematics, 10(3), 1–28.
Cohen, P.C. (1982). A calculating people: The spread of numeracy in early America. Chicago: University of Chicago Press.
Cook, C.J., & Dossey, J.A. (1982). Basic facts thinking strategies for multiplication— revisited. Journal for Research in Mathematics Education, 13, 163–171.
Davis, R.B. (1984). Learning mathematics: The cognitive science approach to mathematics education. Norwood, NJ: Ablex.
Davydov, V.V., & Andronov, V.P. (1981). Psychological conditions of the origination of ideal actions (Project Paper No. 81–2). Madison: University of Wisconsin, Research and Development Center for Individualized Schooling.
Fuson, K.C. (1986a). Roles of representation and verbalization in the teaching of multidigit addition and subtraction. European Journal of Psychology of Education, 1, 35–56.
Fuson, K.C. (1986b). Teaching children to subtract by counting up. Journal for Research in Mathematics Education, 17, 172–189.
Fuson, K.C. (1988). Children’s counting and concepts of number. New York: Springer-Verlag.
Fuson, K.C. (1990). Conceptual structures for multiunit numbers: Implications for learning and teaching multidigit addition, subtraction, and place value. Cognition and Instruction, 7, 343–403.
Fuson, K.C. (1992a). Research on learning and teaching addition and subtraction of whole numbers. In G.Leinhardt, R.T.Putnam, & R.A.Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 53–187). Hillsdale, NJ: Erlbaum.
Fuson, K.C. (1992b). Research on whole number addition and subtraction. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 243–275). New York: Macmillan.
Fuson, K.C., & Briars, D.J. (1990). Using a base-ten blocks learning/teaching approach for first- and second-grade place-value and multidigit addition and subtraction. Journal for Research in Mathematics Education, 21, 180–206.
Fuson, K.C., & Burghardt, B.H. (1993). Group case studies of second graders inventing multidigit addition procedures for base-ten blocks and written marks. In J.R.Becker & B.J.Pence (Eds.), Proceedings of the fifteenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 240– 246). San Jose, CA: San Jose State University. (ERIC Document Reproduction Service No. ED 372 917).
Fuson, K.C., & Burghardt, B.H. (1997). Group case studies of second graders inventing multidigit subtraction methods. In J.A.Dossey, J.O.Swafford, M.Parmantie, & A. E.Dossey (Eds.), Proceedings of the nineteenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 291– 298). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education. (ERIC Document Reproduction Service No. ED 420 494).
Fuson, K.C., & Burghardt, B.H. (in press). Multi-digit addition and subtraction methods invented in small groups and teacher support of problem solving and reflection. In A. Baroody & A.Dowker (Eds.), The development of arithmetic concepts and skills: Constructing adaptive expertise. Hillsdale, NJ: Erlbaum.
Fuson, K.C., De La Cruz, Y., Smith, S., Lo Cicero, A., Hudson, K., Ron, P., & Steeby, R. (2000). Blending the best of the twentieth century to achieve a mathematics equity pedagogy in the twenty-first century. In M.J.Burke (Ed.), Learning mathematics for a new century (2000 Yearbook of the National Council of Teachers of Mathematics, pp. 197–212). Reston, VA: NCTM.
Fuson, K.C., & Fuson, A.M. (1992). Instruction to support children’s counting on for addition and counting up for subtraction. Journal for Research in Mathematics Education, 23, 72–78.
Fuson, K.C., & Kwon, Y. (1991). Chinese-based regular and European irregular systems of number words: The disadvantages for English-speaking children. In K.Durkin & B.Shire (Eds.), Language and mathematical education (pp. 211–226). Milton Keynes, UK: Open University Press.
Fuson, K.C., & Kwon, Y. (1992a). Korean children’s understanding of multidigit addition and subtraction. Child Development, 63, 491–506.
Fuson, K.C., & Kwon, Y. (1992b). Korean children’s single-digit addition and subtraction: Numbers structured by ten. Journal for Research in Mathematics Education, 23, 148– 165.
Fuson, K.C., & Secada, W.G. (1986). Teaching children to add by counting-on with one-handed finger patterns. Cognition and Instruction, 3, 229–260.
Fuson, K.C., Smith, S.T., & Lo Cicero, A.M. (1997). Supporting Latino first graders’ ten-structured thinking in urban classrooms. Journal for Research in Mathematics Education, 28, 738–766.
Fuson, K.C., Stigler, J., & Bartsch, K. (1988). Brief report: Grade placement of addition and subtraction topics in Japan, mainland China, the Soviet Union, Taiwan, and the United States. Journal for Research in Mathematics Education, 19, 449–456.
Fuson, K.C., Wearne, D., Hiebert, J.C., Murray, H.G., Human, P.G., Olivier, A.I., Carpenter, T.P., & Fennema, E. (1997). Children’s conceptual structures for multidigit numbers and methods of multidigit addition and subtraction. Journal for Research in Mathematics Education, 28, 130–162.
Fuson, K.C., & Willis, G.B. (1988). Subtracting by counting up: More evidence. Journal for Research in Mathematics Education, 19, 402–420.
Geary, D.C. (1994). Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association.
Geary, D.C., & Brown, S.C. (1991). Cognitive addition: Strategy choice and speed-of-processing differences in gifted, normal and mathematically disabled children. Developmental Psychology, 27, 298–406.
Ginsburg, H.P., & Allardice, B.S. (1984). Children’s difficulties with school mathematics. In B.Rogoff & J.Lave (Eds.), Everyday cognition: Its development in social contexts (pp. 194–219). Cambridge, MA: Harvard University Press.
Greer, F. (1992). Multiplication and division as models of situations. In D.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 276–295). New York: Macmillan.
Griffin, S.A., Case, R., & Siegler, R.S. (1994). Rightstart: Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure. In K.McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practice (pp. 25–49). Cambridge, MA: MIT Press.
Harel, G., & Confrey, J. (1994). The development of multiplicative reasoning in the learning of mathematics. Albany: State University of New York Press.
Hartung, M.L., Van Engen, H., & Knowles, L. (1955). Seeing through arithmetic. Chicago: Scott Foresman.
Hatano, G. (1988, Fall). Social and motivational bases for mathematical understanding. New Directions for Child Development, 41, 55–70.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Hiebert, J., & Wearne, D. (1993). Instructional tasks, classroom discourse, and student learning in second grade. American Educational Research Journal, 30, 393–425.
Hiebert, J., & Wearne, D. (1996). Instruction, understanding, and skill in multidigit addition and subtraction. Cognition and Instruction, 14, 251–83.
Hope, J.A., & Sherrill, J.M. (1987). Characteristics of unskilled and skilled mental calculators. Journal for Research in Mathematics Education, 18(2), 98–111.
Huinker, D.M. (1991). Effects of instruction using part-whole concepts with one-step and two-step word problems in grade four (Doctoral dissertation University of Michigan, 1990). Dissertation Abstracts International, 52(01), 103 A.
Jerman, M. (1970). Some strategies for solving simple multiplication combinations. Journal for Research in Mathematics Education, 1, 95–128.
Kamii, C. (1989). Young children continue to reinvent arithmetic—2nd grade: Implications of Piaget’s theory. New York: Teachers College Press.
Kamii, C. (1994). Young children continue to reinvent arithmetic—3rd grade: Implications of Piaget’s theory. New York: Teachers College Press.
Kamii, C. & Dominick, A. (1998). The harmful effects of algorithms in grades 1–4. In L. J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 130–140). Reston VA: NCTM.
Kouba, V. (1989). Children’s solution procedures for equivalent set multiplication and division word problems. Journal for Research in Mathematics Education, 20, 147–158.
Labinowicz, E. (1985). Learning from children: New beginnings for teaching numerical thinking. Menlo Park, CA: Addison-Wesley.
Lampert, M. (1986a). Knowing, doing, and teaching multiplication. Cognition and Instruction, 3, 305–342.
Lampert, M. (1986b). Teaching multiplication. Journal of Mathematical Behavior, 5, 241– 280.
Lampert, M. (1992). Teaching and learning long division for understanding in school. In G.Leinhardt, R.T.Putnam, & R.A.Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 221–282). Hillsdale, NJ: Erlbaum.
LeFevre, J., Bisanz, J., Daley, K.E., Buffone, L., Greenham, S.L., & Sadesky, G.S. (1996). Multiple routes to solution of single-digit multiplication problems. Journal of Experimental Psychology: General, 125, 284–306.
LeFevre, J., Sadesky, G.S., & Bisanz, J. (1996). Selection of procedures in mental addition: Reassessing the problem-size effect in adults. Journal of Experimental Psychology: Learning, Memory, and Cognition, 22, 216–230.
Lemaire, P., & Siegler, R.S. (1995). Four aspects of strategic change: Contributions to children’s learning of multiplication. Journal of Experimental Psychology: General, 124, 83–97.
Leutzinger, L.P. (1979). The effects of counting on the acquisition of addition facts in grade one (Doctoral dissertation, University of Iowa, 1979). Dissertation Abstracts International, 40(07), 3765A.
Markovits, Z., & Sowder, J. (1988). Mental computation and number sense. In M.J. Behr, C.B.Lacampagne, & M.M.Wheeler (Eds.), Proceedings of the tenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 58–64). DeKalb: Northern Illinois University. (ERIC Document Reproduction Service No. ED 411 126 ).
Markovits, Z., & Sowder, J. (1994). Developing number sense: An intervention study in grade 7. Journal for Research in Mathematics Education, 25, 4–29.
Matsushita, K. (1994). Acquiring mathematical knowledge through semantic and pragmatic problem solving. Human Development, 37, 220–232.
McClain, K., Cobb, P., & Bowers, J. (1998). A contextual investigation of three-digit addition and subtraction. In L.J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 141–150). Reston, VA: NCTM.
Morrow, L.J., & Kenney, M.J. (Eds.). (1998). The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics). Reston, VA: NCTM.
Mulligan, J., & Mitchelmore, M. (1997). Young children’s intuitive models of multiplication and division. Journal for Research in Mathematics Education, 28, 309–330.
Murray, H., Olivier, A. & Human, P. (1992). The development of young children’s division strategies. In W.Geeslin & K.Graham (Eds.), Proceedings of the Sixteenth International Conference for the Psychology of Mathematics Education (vol. 2, pp. 152–159). Durham, NH: PME Program Committee. (ERIC Document Reproduction Service No. ED 383 538).
Nesher, P. (1992). Solving multiplication word problems. In G.Leinhardt, R.T.Putnam, & R.A.Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 189–220). Hillsdale, NJ: Erlbaum.
Nunes, T. (1992). Ethnomathematics and everyday cognition. In D.A.Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 557–574). New York: Macmillan.
Olivier, A., Murray, H. & Human, P. (1990). Building on young children’s informal mathematical knowledge. In G.Booker, P.Cobb, & T.N.Mendicuti (Eds.), Proceedings of the Fourteenth International Conference for the Psychology of Mathematics Education (vol. 3, pp. 297–304). Oaxtepec, Mexico: PME Program Committee. (ERIC Document Reproduction Service No. ED 411 139).
Rathmell, E.C. (1978). Using thinking procedures to learn basic facts. In M.Suydam (Ed.), Developing computational skills (1978 Yearbook of the National Council of Teachers of Mathematics, pp. 13–38). Reston, VA: NCTM.
Rathmell, E., & Huinker, D. (1989). Using “part-whole” language to help children represent and solve word problems. In P.R.Trafton (Ed.), New directions for elementary school mathematics (1989 Yearbook of the National Council of Teachers of Mathematics, pp. 99–110). Reston, VA: NCTM.
Rathmell, E.C., & Trafton, P.R. (1990). Whole number computation. In J.R.Payne (Ed.), Mathematics for the young child (pp. 153–172). Reston, VA: National Council of Teachers of Mathematics.
Resnick, L.B. (1983). A developmental theory of number understanding. In H.P.Ginsburg (Ed.), The development of mathematical thinking (pp. 110–152). Hillsdale, NJ: Erlbaum.
Resnick, L.B., & Ford, W.W. (1981). The psychology of mathematics for instruction. Hillsdale, NJ: Erlbaum.
Reys, R.E., Rybolt, J.F., Bestgen, B.J., & Wyatt, J.W. (1982). Processes used by good computational estimators. Journal for Research in Mathematics Education, 13, 183–201.
Riley, M.S., & Greeno, J.G. (1988). Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction, 5, 49–101.
Rittle-Johnson, B., & Alibali, M.W. (1999). Conceptual and procedural knowledge of mathematics: Does one lead to the other? Journal of Educational Psychology, 91, 175– 189.
Rittle-Johnson, B., & Siegler, R.S. (1998). The relation between conceptual and procedural knowledge in learning mathematics: A review. In C.Donlan (Ed.), The development of mathematical skills (pp. 75–110). East Sussex, UK: Psychology Press.
Ron, P. (1998). My family taught me this way. In L.J.Morrow & M.J.Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 115–119). Reston, VA: NCTM.
Rubenstein, R.N. (1985). Computational estimation and related mathematical skills. Journal for Research in Mathematics Education, 16, 106–119.
Saxe, G.B. (1982). Culture and the development of numerical cognition: Studies among the Oksapmin of Papua New Guinea. In C.J.Brainerd (Ed.), Progress in cognitive development research: Vol. 1: Children’s logical and mathematical cognition (pp. 157–176). New York: Springer-Verlag.
Saxe, G.B. (1988). The mathematics of child street vendors. Child Development, 59, 1415– 1425.
Siegler, R.S. (1996). Emerging minds: The process of change in children’s thinking. New York: Oxford University Press.
Siegler, R.S. (in press). Implications for cognitive science research for mathematics education. In J.Kilpatrick, W.G.Martin, & D.E.Schifter (Eds.), A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
Siegler, R.S., & Jenkins, E. (1989). How children discover new strategies. Hillsdale, NJ: Erlbaum.
Sowder, J.T. (1992). Making sense of numbers in school mathematics. In G.Leinhardt, R.Putnam, & R.A.Hattrup (Eds.), Analysis of arithmetic for mathematics teaching (pp. 1–51). Hillsdale, NJ: Erlbaum.
Sowder, J.T., & Wheeler, M.M. (1989). The development of concepts and procedures used in computational estimation. Journal for Research in Mathematics Education, 20, 130–146.
Steffe, L. (1994). Children’s multiplying schemes. In G.Harel & J.Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 3–39). Albany: State University of New York Press.
Steffe, L.P., Cobb, P., & von Glasersfeld, E. (1988). Construction of arithmetical meanings and procedures. New York: Springer-Verlag.
Stigler, J.W. (1984). “Mental abacus”: The effect of abacus training on Chinese children’s mental calculation. Cognitive Psychology, 16, 145–176.
Steinberg, R. (1985). Instruction on derived facts strategies in addition and subtraction. Journal for Research in Mathematics Education, 16, 337–355.
Thornton, C.A. (1978). Emphasizing thinking strategies in basic fact instruction. Journal for Research in Mathematics Education, 9, 214–227.
Uttal, D.H., Scudder, K.V., & DeLoache, J.S. (1997). Manipulatives as symbols: A new perspective on the use of concrete objects to teach mathematics. Journal of Applied Developmental Psychology, 18, 37–54.
VanLehn, K. (1986). Arithmetic procedures are induced from examples. In J.Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 133–179). Hillsdale, NJ: Erlbaum.
Vergnaud, G. (1983). Multiplicative structures. In R.Lesh & M.Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 127–174). New York: Academic Press.
Verschaffel, L., & De Corte, E. (1993). A decade of research on word-problem solving in Leuven: Theoretical, methodological, and practical outcomes. Educational Psychology Review, 5(3), 1–18.