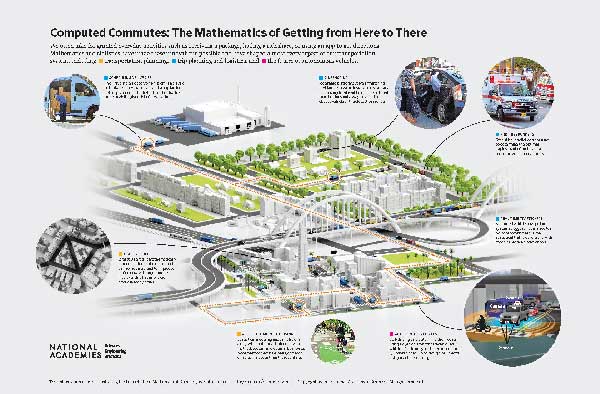
Computed Commutes: The Mathematics of Getting from Here to There

Transportation Planning

Mathematical and statistical sciences have created many tools that decision-makers use in transportation planning. These tools allow us to better understand the expected impact of changes to infrastructure. For example, mathematical and statistical sciences allow us to answer questions such as the following:

• How would constructing a new subway line across a key waterway impact public transportation?
• Would adding a new road cut down on traffic jams? Could it make it worse?
• Would converting a lane to carpool-only decrease pollution?
• How would closing a section of road to make it pedestrian-only impact congestion and pedestrian safety?
• How would replacing street parking with a bike lane impact traffic and local businesses?

The answers to these questions are not always straightforward. For example, adding new roads does not always improve traffic flow. Braess’s Paradox is a mathematical observation discovered in 1968 that explains how adding a new road to an existing road network can actually slow down the overall traffic flow through it and, similarly, how sometimes adding or widening a road can make traffic worse. For example, researchers showed that closing certain roads in New York City and Boston would actually improve traffic flow. Based on this mathematical analysis, policy-makers in New York City closed Times Square to cars and found that it did not increase congestion in the city. 

 

Trip Planning and Logistics

Mathematical and statistical sciences are the foundation on which modern routing, mapping, and turn-by-turn directions are based. The important insights and methods that these sciences have developed allow us to easily and quickly answer questions like the following:

• What is the fastest route from a driver’s current location to their destination, taking into account traffic conditions? What other factors (such as distance and number of turns) should be taken into account when recommending a route? How long will the trip take?
• Where should ambulances be positioned as they wait to be dispatched? Once an ambulance is dispatched, what is the best way to reposition the remaining ambulances?
• What is the best way to match rideshare drivers or taxis and riders to minimize wait times?
• What is the best way to assign packages to delivery trucks? What is the most efficient way to route each individual truck for deliveries?
• How should ride-hailing platforms price services to balance the supply of drivers with the demand of passengers?

 

A famous example is the Traveling Salesperson Problem where an optimal route is determined for a salesman to visit specific houses or, more recently, a delivery truck to drop off packages. Deciding on these routes involves mathematical optimization—in particular, the subfield of mixed integer programming. The complexity of these analyses grows exponentially as the number of stops increases and gets even more complicated when trying to plan a route in real time under changing conditions (such as rescheduling deliveries when packages are delayed due to bad weather). These solutions often involve clever mathematical manipulations that enable them to be approximated efficiently.

The technology for mapping has evolved considerably in recent years. Mathematics is used to identify optimal routes given traffic trends that best satisfy various goals like shortening travel time or distance and prioritizing road type (highway versus surface street). Mathematical and statistical sciences have made major strides in estimating total travel time for planned trips, taking traffic into account using a combination of real-time and historical data. And, these aren’t typically one-time analyses. Evolving traffic and road conditions require that these large data analyses be continually refreshed to enable dynamic decision-making, such as rerouting to avoid a traffic jam.

Researchers have studied the deployment of emergency vehicles using agent-based models that simulate the paths of first responders to an emergency. These models use statistical predictions to estimate how long it takes to travel each segment of road using historical data on traffic and movement. The simulations can be used to figure out an optimal way to organize and deploy ambulances and redeploy them.

Mathematical sciences are also the key to matching riders to drivers in ride-hailing systems. It may seem ideal to match the driver with the shortest expected pickup time, but the total wait for pickup across all riders can actually be minimized by solving a matching problem across a batch of requests.

The Future of Autonomous Vehicles

Mathematical and statistical sciences are critical to the next-generation of autonomous and semi-autonomous vehicles. Self-driving cars rely on what is known as simultaneous localization and mapping (SLAM) algorithms from computational geometry. Using sensor readings from LIDAR, RADAR, GPS, and various cameras, SLAM creates a real-time map of the current area and the vehicle’s position within that map. Bayesian statistical techniques are used to capture inherent uncertainty and characterize the most likely situations. Machine learning techniques, such as deep neural networks, are used for object recognition to identify road signs, other vehicles, and pedestrians.

However, numerous challenges persist. Self-driving vehicles are currently only available in limited circumstances—in part, because they depend upon highly accurate maps, real-time analysis of substantial amounts of diverse sensor data, and effective tracking of other moving objects. Mathematical and statistical science will likely offer the key to solving these difficult problems.