APPENDIX E Probability and Reliability Analysis
WHAT IS PROBABILITY?
Probability is a number between 0 and 1 that expresses a degree of uncertainty about whether an event, such as an accident, will occur. A logically impossible event is assigned the number 0, and a logically certain event is assigned the number 1. The axioms of probability tell us how to combine various uncertainties.
Interpretations of Probability
There are at least four interpretations of probability:
-
classical (equally likely)
-
logical (the "necessarist" position)
-
relative frequency (objectivistic)
-
personalistic (subjectivistic)
The classical interpretation is based on the "principle of insufficient reason" and was advocated by the determinists Bernoulli, Laplace, De Moivre, and Bayes. This interpretation has limited applicability and is now subsumed under the personalistic interpretation.
The logical interpretation was favored by logicians, such as Keynes, Reichenbach, and Carnap, and is currently out of vogue.
The relative frequency interpretation is used by many statisticians and is currently the most favored. This interpretation requires the conceptualization of an infinite collective and is not applicable in one-of-a-kind situations.
The personalistic interpretation is more universal and incorporates engineering and other knowledge. This interpretation is popular in many applications, including risk analysis and safety analysis.
Axioms of Probability: Dependence and Independence
All the interpretations of probability have a common set of axioms that tell us how to combine probabilities of different events. But why should risk analysts be interested in such mathematical details? Because one of the axioms pertains to the notion of dependence (and independence), a matter that is not carefully addressed by either the FAA or industry.
Consider two events ε1 and ε2:
For example, let
Then, the axioms are:
|
|
(convexity) |
|
|
(addition) |
|
|
(multiplication)1 |
FAULT TREE ANALYSIS
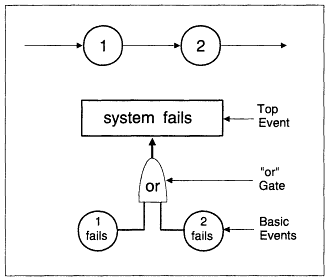
Fault tree analysis is an engineering tool that, among other things, can help assess probabilities of the occurrence of undesirable events. The undesirable event is called the "top event."
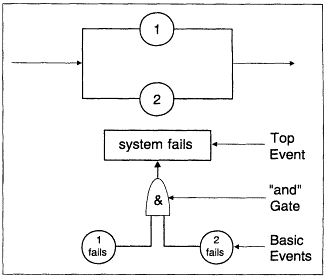
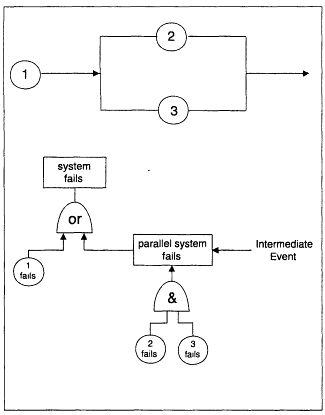
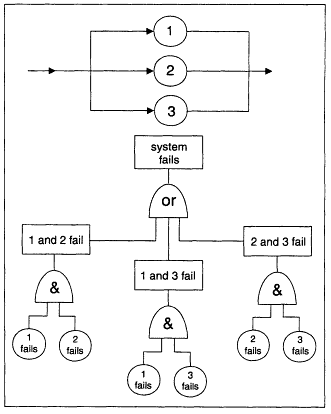
The "and" and "or" gates of a fault tree correspond to the ''and" and the "or" functions in the axioms (or the calculus) of probability. At the very bottom of the tree are "basic events,'' which usually correspond to equipment failures. Fault trees are similar to block diagrams of a system. Examples are illustrated in Figures E-1 through E-4.
Assessing Top Event Probabilities
How do we obtain P(T.E.)? This is the subject of reliability analysis wherein mathematical models, expert judgment, failure data, and maintenance come into play. Consider the following cases.
Series System with "Independence"
When ε1 and ε2 are dependent, we need sophisticated reliability models to evaluate P(T.E.), as discussed below.
Parallel System with "Independence"
Series-Parallel System with Independence
Two-out-of-Three System
ASSUMPTIONS OF INDEPENDENCE
In general, assuming independence under an "and" gate underestimates the probability of the top event (an accident or incident). Conversely, assuming independence under an "or" gate overestimates the probability of the top event. The assumption of independence is an idealization often made routinely because it simplifies the analysis, but the consequences can be severe. Thus, to avoid a false sense of security, it is important that risk analysis procedures and documents used by both industry and the FAA treat dependence/ independence properly.
EXAMPLE INCORPORATING DEPENDENT FAILURES
Consider a twin engine aircraft. To calculate the probability that both engines will fail by the time the aircraft accumulates some number of operating hours, τ, it is necessary to develop a probability model. A simple model is to assume that the time to engine failure has an exponential distribution with failure rate, λ, and that the failure rates are independent of each other. For that case, the probability that both engines will fail simultaneously is:
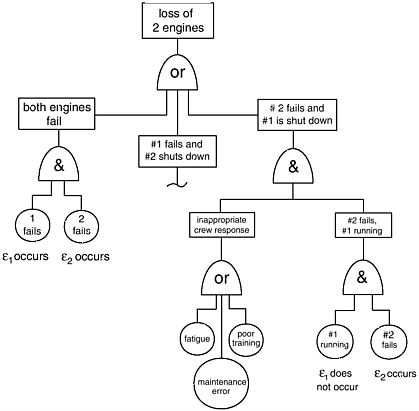
FIGURE E-5 Fault tree diagram of dual-engine failure.
A more sophisticated approach is to consider the possibility of dependent or common mode failures. For example, Figure E-5 illustrates the possibility that a failure in one engine could prompt the flight crew to shut down the functional engine, which would result in the loss of both engines even though only one engine malfunctioned. A model for common mode failures can be created via a new parameter λ*. Now,
Clearly, the two probabilities are different. This shows that independence underestimates the risk of both engines failing.