Page 137
3
Novel Quantum Phenomena
One might imagine that because condensed-matter and materials physics deals with known objects (atoms) interacting via well-defined and well-under-stood forces (the Coulomb interaction among charged particles) there are no surprises and no fundamental intellectual challenges left to be discovered. Nothing could be farther from the truth. Quantum mechanics is a strange business, and the quantum mechanics of large collections of atoms and molecules can be stranger still. It inevitably happens that when assembling a collection of atoms to form a material, the whole is greater than the sum of the parts in the sense that "emergent phenomena," such as spontaneously broken symmetries and quantum or classical phase transitions, often appear in large collections of atoms. For example, a set of widely spaced copper atoms has an energy gap for charge excitations and thus is an insulator. This is because the atoms are largely independent of each other and retain the discrete spectra of isolated atoms. Even at absolute zero, compressing the atoms into solid copper causes the electrons to "melt" into a new ''liquid" phase that has no excitation gap and is an excellent electrical conductor. If the same experiment is carded out with aluminum atoms, very subtle differences in the atomic properties lead not to an ordinary metal but to a superconductor. There exist vast families of complex materials, with many atoms per unit cell, whose surprising properties are still extremely difficult to predict a priori. This is an especially important challenge for theoreticians in the coming decade.
The idea of emergent phenomena teaches us that, even though we understand and can relatively easily compute the properties of individual atoms, materials constructed from large collections of atoms will routinely surprise us with com-
Page 138
pletely unexpected properties. Living matter and life itself are perhaps the most spectacular examples of emergent phenomenon; no matter how much we learn about individual atoms, life cannot be understood or explained in this purely reductionist manner. One of the biggest surprises of the last decade was high-temperature superconductivity. It is hard to imagine a less likely candidate for a superconductor than an insulating ceramic compound with properties similar to those of a china coffee cup. Yet when chemically doped to introduce charge carriers, such compounds not only superconduct, they do so at record high temperatures.
The characteristic energy scale for individual atoms is 1 to 10 electron volts (eV). However, as we look on larger length scales at collections of atoms, characteristic energies become smaller and smaller, and excitations become more and more collective. At low energies, the effective elementary degrees of freedom may be collective objects very different from individual electrons and atoms, and their effective interactions may be very different from the original ''bare" Coulomb interactions. These collective effects are the source of the surprises that emerge.
It is instructive to compare this situation with that in high-energy elementary particle physics. There we know the effective degrees of freedom and their interactions at low energies—it is the world of atoms around us. The intellectual challenge is to understand degrees of freedom at shorter and shorter length scales and higher and higher energy scales. This is done by constructing high-energy particle accelerators to act as microscopes with ever greater magnification, or by studying extreme conditions in astrophysical systems and the early universe. This approach is just the reverse of what is done in condensed-matter physics, where we strive to understand collective effects at longer and longer length scales. The analog of the particle accelerator is the refrigerator, which lowers thermal energy scales and increases the distance over which particles suffer inelastic collisions. The analog of an extreme astrophysical system is a sample in a dilution refrigerator. The intellectual challenge is the same in the two fields: to find correct descriptions of the physics that work over a wide range of scales.
Fifty years ago understanding a novel quantum object known as a "hole" (see Box 3.1) led to the invention of the transistor. In the past decade there has been tremendous progress in the discovery and study of a variety of novel quantum phenomena. This chapter presents brief descriptions of a few examples drawn from superfluidity, superconductivity, Bose-Einstein condensation, quantum magnetism, and the quantum Hall effect. It cannot cover many other fascinating areas of development in the last decade, including significant advances in our understanding of quantum critical phenomena, non-Fermi liquids, metal-insulator and superconductor-insulator transitions in two dimensions, quantum chaos and the role of interactions, coherence, and disorder in mesoscopic systems.
There has been particularly significant progress in this last area, both technologically and theoretically. For example, electron "wave guides" have been constructed, and the quantization of their conductance in units of e2/h has been
Page 139
| BOX 3.1 Exotic Quantum Objects in Today's Technology |
| Fifty years ago at the time of the invention of the transistor, the hot topic in condensed-matter physics was an exotic quantum object, the "hole," whose predicted existence was one of the great early triumphs of quantum mechanics. The ability to create and manipulate these "holes" is crucial to the operation of diodes, transistors, photocells, light-emitting diodes, solid-state lasers, and computer chips. |
| To understand the concept of the hole, consider the fact (illustrated schematically in Figure 3.1.1) that when atoms are assembled into a solid, the discrete quantum energy levels of the individual atoms smear out into bands of quantum levels. The Pauli exclusion principle tells us that each band state can hold no more than one electron. In a semiconductor, the highest occupied band (the valence or "bonding" band) is separated by a small but crucially important energy gap from the lowest unoccupied band (the conduction or "anti-bonding" band). |
| The Pauli exclusion principle has the important consequence that a filled band is inert. It is impossible to excite the system by moving an electron to a new state within a band that is already entirely filled up, so the only way to achieve the lowest energy excitation that can be made in a semiconductor is to lift an electron from the valence band across the gap to the conduction band. It is easy to visualize the electron in the conduction band as a particle that can move around, carry current and so forth. Paradoxically, quantum mechanics also teaches us that the absence of an electron in the otherwise-filled valence band should be viewed as a hole that behaves like a kind of anti-particle (much like the positron, which is the anti-particle of the electron in high-energy physics). Without the hole, the valence band is inert and carries no charge or current. The electron that was removed had negative charge and carried some particular current. Hence, we must assign the hole a positive charge and the opposite current. Without quantum mechanics guaranteeing that a filled band is inert, this assignment would not be meaningful. |
| Introduction of chemical dopants into semiconductors can produce an excess of electrons (n-type material) or an excess of holes (p-type material). Remarkable materials physics advances in purification and doping control of silicon now allow routine inexpensive construction of the special types of junctions between p- and n-type material that play such a crucial role in today's solid-state technology. So next time you turn on your computer, remember quantum mechanics is at work! |
|
|
| Figure 3.1.1 Energy bands in solids. [Reprinted with permission from S.M. Girvin, "Exotic quantum order in low-dimensional systems," Solid State Communications 107, 623 (1998). Copyright © 1998 Elsevier Science.] |
Page 140
observed. It is also now possible, for example, to construct mesoscopic grains of metal large enough to be superconducting but small enough that significant changes in transport properties are observed depending on whether the number of electrons on the grain is even or odd. In addition, we now have observations of interference effects for electrons diffusing in a mesoscopic normal conductor bounded by segments of superconductors with variable relative phase.
One of the significant characteristics of condensed-matter and materials physics that is worth emphasizing is the close interaction between experimentalists and theorists. Unlike many other areas of physics, theorists often collaborate closely with experimental groups and they frequently jointly publish papers. The field owes its intellectual vitality to this close collaboration and to a continuous and exciting stream of quite unexpected experimental discoveries.
Newly uncovered electronic phenomena in complex and strongly interacting materials have challenged fundamental theoretical paradigms such as the Fermi liquid. In some cases, such as for the fractional quantum Hall effect, entirely new concepts (for example, fractionally charged quantum vortices) have been developed that enriched the foundations of the field and beautifully explained the new phenomenology. High-temperature superconductivity and heavy-fermion systems present a bewildering array of paradoxes that have spawned many new paradigms whose validity is still being sorted out. This challenge will require, and will lead to, fundamental experimental and theoretical advances in the next decade.
Superfluidity and Superconductivity
Superfluids and superconductors have the remarkable property of carrying matter or charge currents completely without friction. In helium-4, the atoms undergo Bose-Einstein condensation (see next section) and become superfluid a few degrees above absolute zero. In a superconductor, pairs of electrons join together to form an effective boson-like degree of freedom. In an ordinary low-temperature superconductor, these Cooper pairs of electrons have a diameter much larger than the spacing between the electrons. Hence, it is not usually appropriate to view the superconducting phase transition as Bose-Einstein condensation, though it is closely related.
The 1996 Nobel Prize in Physics was awarded to Lee, Osheroff, and Richardson for the discovery of superfluidity in helium-3 (see Table O.1). This isotope of helium is a fermion, and it is Cooper pairs of helium-3 atoms that just barely condense at exceedingly low temperatures. Unlike the electrons in an ordinary superconductor, which form pairs in a state of zero relative angular momentum, helium-3 atoms pair in a p-wave (![]() ) angular momentum state. This feature gives superfluid helium-3 many novel properties because the state of the system is determined not just by the complex phase of the condensate wave function, but also by the local orientation of the pair angular momentum vector. The exotic pairing state of helium-3 is naturally connected with high-
) angular momentum state. This feature gives superfluid helium-3 many novel properties because the state of the system is determined not just by the complex phase of the condensate wave function, but also by the local orientation of the pair angular momentum vector. The exotic pairing state of helium-3 is naturally connected with high-
Page 141
temperature superconductors for two independent reasons. First, it has recently been established via several ingenious experiments that the pairing state in high-temperature superconductors is d-wave (![]() ), rather than the usual s-wave (
), rather than the usual s-wave (![]() ). Unlike the case of helium-3, however, the direction of the angular momentum is not free to change but is fixed by the underlying lattice. In fact, as illustrated in Figure 3.1, the d-wave is actually a standing wave with the angular positions of its antinodes parallel to the axes of the square copper oxide planes.
). Unlike the case of helium-3, however, the direction of the angular momentum is not free to change but is fixed by the underlying lattice. In fact, as illustrated in Figure 3.1, the d-wave is actually a standing wave with the angular positions of its antinodes parallel to the axes of the square copper oxide planes.

Figure 3.1
(Left) The long straight lines mark the boundaries of three substrate strontium titanate films with different crystallographic orientations. The four circles are rings of the high-temperature superconductor yttrium barium copper oxide, grown epitaxially on the substrate. The substrate orients the dx2-y2 Cooper pair wave function as indicated by the four-leaf clovers. At the point where the ring crosses from one substrate to the next it has a grain-boundary Josephson junction. Cooper pairs moving from the lower section to the upper left suffer an orientation change of less than 45 degrees and hence have a positive overlap with their new state. The same is true for tunneling from the upper left to the upper right. However, the orientation change from the upper right to the lower section exceeds 45 degrees and hence gives a negative overlap. A Cooper pair traveling around the central ring thus picks up a net minus sign (a phase shift of p), which results in destructive interference that raises the energy. The other three rings remain unfrustrated. The frustration of the central ring can be alleviated if a spontaneous current begins to circulate, which produces a half quantum of magnetic flux, because the Aha-ronov-Bohm effect would then introduce an additional ±p phase shift. This saves more than enough energy to pay for the cost of producing the current. Thus, if the superconductor is d-wave, the system is unstable to producing half a flux quantum trapped in the central ring. The bright spot in the central ring is an image based on a scanning-probe measurement, using superconducting quantum interference devices, of the local magnetic field. [Reprinted with permission from Barbara Levi, Physics Today 49, 19-22 (1996). Copyright © 1996 American Institute of Physics.] (Right) The same data are shown but in a three-dimensional representation. The total integrated flux in the central ring is very close to half a flux quantum, providing proof that the system is frustrated and is almost certainly d-wave. [Reprinted with permission from Nature 373, cover page (January 9,1995). Copyright © 1995 Nature.]
Page 142
One novel feature of d-wave superconductivity is that scattering at interfaces and nonmagnetic scattering by disorder can be pair-breaking. This effect has come to the fore recently because of evidence that has been obtained suggesting that certain crystal faces of high-Tc materials spontaneously break time-reversal symmetry by nucleating an additional pairing channel (for which surface scattering is not pair-breaking) to form a complex gap function.
The second similarity between the oxides and superfluid helium-3 is that both are strongly correlated systems. The oxides, however, are unusual in that the coherence length (size of a Cooper pair) is small, comparable to the spacing between the particles, which means that the transition bears a closer resemblance to Bose-Einstein condensation. Fluctuation effects are far more important than in an ordinary superconductor because mean field theory relies for its validity on there being a very large number of particles within the volume occupied by each Cooper pair.
Understanding strong correlation effects is an important challenge for both the superconducting state and the unusual normal state of these materials. At present there is no clear understanding of the mechanism for high-temperature superconductivity. We do not know, for example, whether the superconductivity occurs because of, or in spite of, antiferromagnetism. Indeed, it is not unreasonable to ask whether the phrase "the mechanism" is even meaningful in this case.
Superfluid helium-3 is a strongly correlated Fermi liquid that just barely manages to form Cooper pairs. It is not yet clear how to describe the corresponding strong correlations in high-temperature superconductors. The strange properties of the normal state—for example, the extremely linear temperature dependence of the resistivity—may mean that the standard theory of Fermi liquids cannot be used to describe them. If so, a totally new paradigm will have to be developed. Ideally, it will be possible to develop a simple picture that captures the essential physics and allows us to construct new materials with even higher critical temperatures, perhaps even higher than room temperature.
The small size of Cooper pairs in high-temperature superconductors has the benefit that, at least naively, it increases their tolerance for very strong magnetic fields. However, it may also be one of the many factors that limit the critical currents in these materials. Despite the technological problems caused by this latter effect, and despite the difficult materials problems, progress is being made toward practical applications of high-Tc materials.
Study of the short coherence length and associated strong fluctuations of the order parameter in high-Tc materials has led to some interesting and fundamental advances in statistical mechanics. The theoretical ideas that have been developed are directly relevant to technological problems presented by the strong suppression of the critical current by magnetic fields. Because of their short coherence length, high-Tc superconductors are strongly type-II. This means that an applied magnetic field penetrates the sample relatively uniformly, inducing a high density of vortex lines.
Page 143
Application of a current produces a driving force that pushes the vortices sideways, leading to dissipation of energy. Naturally occurring or artificially introduced disorder produces random traps that tend to impede the motion of the vortices. One of the deep questions about this random statistical mechanical system is whether, in the limit of a weak driving force, the vortices are perfectly pinned. That is, is the linear response resistivity ever truly zero at any finite temperature? More colloquially, is a superconductor in a magnetic field really a superconductor?
For many years it was thought that the answer to this question was no. The rate of vortex "creep" was known to become extremely small at low temperatures, but it was believed to be thermally activated, giving a never-vanishing resistivity of the form r ~ e-e/kBT. The physical picture behind this is that there is a characteristic energy barrier e, associated with the random pinning, which is finite and can be overcome by thermal fluctuations.
In low-temperature superconductors this question, although important in principle, is nearly moot in practice because the barrier e tends to be large relative to typical thermal energies at Tc The pinning is thus extremely effective at all temperatures where superconductivity exists. In high-Tc materials, the pinning barrier e is smaller (another side effect of the short coherence length) and Tc is much larger. Hence, magnetic fields induce high dissipation rates, which allows the temperature dependence to then be followed over a significant range below the zero-field Tc.
It is now understood that the correct answer to our question—Is a superconductor in a magnetic field really a superconductor?—is yes. As the temperature is lowered, the highly fluctuating "tangled spaghetti" of vortex lines begins to exhibit collective correlations over a length scale x that diverges at a characteristic "vortex glass" temperature Tg.
Associated with this diverging length is a divergence in the effective collective pinning barrier e ~ |T-Tg|-q. Below this temperature the barrier is infinite and cannot be overcome by (equilibrium) fluctuations. The linear-response resistivity is thus truly zero, not merely small.
The existence of a distinct vortex glass phase, as shown in Figure 3.2, makes clear the point that the upper critical field Hc2 is a purely mean-field concept. In mean-field theory, the sample is "normal" for H > Hc2 and "superconducting" for H << Hc2. We now understand that Hc2 is merely a crossover scale below which the order parameter rapidly becomes large. Because of the strong fluctuations in high-Tc materials, there is a ''vortex liquid" regime in which the resistivity is finite even though the superconducting order parameter is large. Only when the system enters the frozen vortex glass phase does a true phase transition occur. Only when the vortices are frozen in place does the dissipation vanish.
Because of the "floppiness" of vortex lines in high-Tc materials (because of the short coherence length and the extremely weak coupling between copper oxide planes along the c axis), random point defects are not very effective at
Page 144
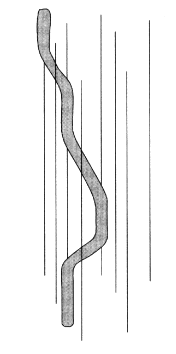
Figure 3.2
One can interpret classical superconductor vortex lines as world lines of quantum bosons moving in two space dimensions and one time dimension. In the Feyn-man-path-integral formulation of quantum statistical mechanics, the trajectories of the bosons must be followed over a time interval h/kBT. Hence the thickness of the superconducting sample determines the inverse "temperature" of these fake quantum bosons. Notice that the columnar defects constitute a potential for the bosons that is random in space but constant in time. Thus we have the quantum mechanics of bosons in two dimensions in the presence of a static random potential. There has been a great deal of interest in the last decade in this "dirty boson" problem as a model for helium in porous media (or adsorbed on surfaces) and for modeling the superconductor-insulator transition in metallic films (viewing the Cooper pairs as bosons). There are two different phases at zero temperature: at low densities or strong disorder, insulating ''Bose glass" phase; at high densities or weaker disorder, the bosons are condensed into a superfluid state. We can now map these pictures back onto the vortex system: The ''insulating Bose glass" phase is superconducting because the vortices are localized. The "superfluid" state of the bosons means that the vortices are freely moving (even though they are highly entangled). Thus the "vortex liquid" has dissipation and represents the nonsuperconducting state. This "Bose glass" generalization of the vortex glass idea can be pursued further to include analogs of the Mott-Hubbard Bose insulator, Mott variable range hopping, and boson tunneling between localized states. Furthermore, our knowledge of the dynamical structure factor for quantum bosons makes predictions for the static structure factor for the vortex fluctuations that have been confirmed by small-angle neutron scattering experiments.
Page 145
pinning. The vortex glass phase does not exist in two dimensions, and it exists in three dimensions only in the absence of magnetic screening (so that collective effects are sufficiently strong).
The pinning efficiency for extended columnar defects is much better. These can be constructed using the linear damage tracks produced by fast-moving heavy ions from an accelerator. The statistical mechanics of fluctuating vortices in this situation has an elegant interpretation by means of an analogy with the quantum mechanics of a Bose liquid (see Figure 3.2).
This quantum boson analogy clearly demonstrates the existence of a phase transition in which the vortices can become localized by columnar pins leading to a state with truly zero resistivity in linear response.
The relatively small size of the Cooper pairs in high-temperature superconductors puts the superconducting transition in a new regime, closer to the Bose-Einstein condensation limit.
The most extreme regime of Bose-Einstein condensation has recently been achieved with the creation of condensates in gases of alkali metal atoms held in atom traps and cooled to nanokelvin temperatures. These are analogous to helium-4 in the sense that the particles are bosonic, but in this case the gas is dilute—the spacing between particles is much larger than the scattering length—and, hence, represents the nearly ideal case of pure Bose-Einstein condensation.
Bose-Einstein Condensation in Atom Traps
Tremendous excitement has been generated by the recent success of the atomic physics community in creating Bose-Einstein condensates (BECs) in dilute gases of alkali atoms. A BEC is a coherent state of matter (see Figure 3.3) in which a finite fraction of the particles occupy the same quantum state. The indistinguishability of the particles and the fact that below the critical temperature their thermal de Broglie wavelengths exceed their spacing are central to the phenomenon. Using a two-stage process of laser cooling followed by evaporative cooling to temperatures on the order of 100 nanokelvin, it is now possible to produce condensates containing a few million atoms in an atomic trap.
BECs have been important in condensed-matter and high-energy physics for many years. BECs were first observed in superfluid helium in 1938. More recently, evidence has been obtained for condensation of excitons in semiconductors. BEC is also believed to provide the mechanism for generating the masses of the hadronic elementary particles.
What is new here is the parameter range; atomic vapors represent an unprecedented low-density regime in which the scattering length (the effective size of the particles) is much smaller than the typical particle spacing. This opens up a new range of possible experiments in which one can control the number of particles, the density, and the atomic species, thereby giving the possibility of varying, and therefore studying, effective interaction strengths in ways that have
Page 146
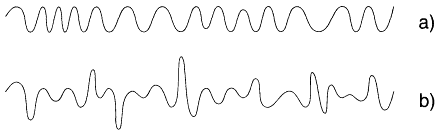
Figure 3.3
A laser produces coherent light, which we can think of as Bose condensate of photons. Understanding what this means can help us understand Bose-Einstein condensates (BECs) and atom lasers. Laser light wave oscillations are very similar to the waves produced by an ordinary radio transmitter, as shown in a. Because nothing fixes the phase of an oscillator, the phase undergoes a slow random walk, but the amplitude fluctuates very little. The random walk of the phase introduces a finite correlation time and hence a small but finite spectral bandwidth. A thermal source of the same bandwidth could be obtained by passing black-body radiation through a narrow filter. The resulting wave would look something like that shown in b. The large amplitude fluctuations are a result of interference among the different Fourier components, each of which has a random amplitude and phase. If the intensity and bandwidths are the same, the autocorrelation functions will be very similar. To distinguish coherent light from incoherent, we therefore have to look at fluctuations. For a perfectly coherent state there are no fluctuations: <Y† Y† YY>-<Y† Y>2 = 0. The quantum mechanical interpretation of this is that the photons are Poisson distributed independently of each other, so that there is no bunching. For a thermal source, the fields are gaussian random variables and Wick's theorem tells us that <Y† Y† YY> = 2! <<Y† Y>2, so that there are very large intensity fluctuations. The quantum interpretation is that there is excess "noise" or "bunching" in the photon distribution. In the atom trap, the potential energy of the short-range interacting bosons is given by the probability of finding two bosons at the same place at the same time, ![]() . Experiments comparing the normal and condensed states at the same density have shown that, just as expected, <V>normal/<V>condensed = 2!. The atomic vapor is unstable to decay into bound atom pairs, which fall (literally) out of the trap. Because a third body is needed to carry off the binding energy, the decay rate obeys <<Y† Y† Y† YYY>normal/<<Y† Y† Y† YYY>condensed = 3!. Remarkably, this third-order coherence effect has also been observed experimentally. Thus an atom trap emitting a coherent beam of alkali atoms (a ''boser") has all the coherence properties of a laser.
. Experiments comparing the normal and condensed states at the same density have shown that, just as expected, <V>normal/<V>condensed = 2!. The atomic vapor is unstable to decay into bound atom pairs, which fall (literally) out of the trap. Because a third body is needed to carry off the binding energy, the decay rate obeys <<Y† Y† Y† YYY>normal/<<Y† Y† Y† YYY>condensed = 3!. Remarkably, this third-order coherence effect has also been observed experimentally. Thus an atom trap emitting a coherent beam of alkali atoms (a ''boser") has all the coherence properties of a laser.
not been possible in traditional condensed-matter systems. In addition, some of the characteristic timescales are extremely slow (fractions of a second) opening up the possibility of studying macroscopic quantum coherence effects in a totally new time domain.
The other aspect that is new is the unprecedented ability to dynamically change the trap parameters and optically probe the detailed response of the condensate. It is now possible, for example, to measure such quantities as the
Page 147
potential energy stored in the condensate and the momentum distribution function. In addition, it is possible to suddenly remove a barrier between two condensates and directly see the quantum interference fringes that result from their overlap. In the future it will likely be possible to extend these results to multicomponent condensates and study the separate response of each component.
Atomic condensates have played a truly useful role in promoting cross-disciplinary communication and productive interactions among the condensed-matter, atomic-physics, and quantum-optics communities. The condensed-matter theory community is supplying expertise in two areas: many-body calculation techniques and experience with the study of collective effects. It turns out that in this low-density regime, straightforward and standard mean-field theory calculation methods appear to be quite accurate for low temperatures, so there appear to be few theoretical challenges in this regard (except for questions of metastability for systems with negative scattering lengths that have not yet been fully settled). On the other hand, there remain quite a few challenges in understanding collective effects. These include the mechanism for damping of collective modes at finite temperatures, two-fluid hydrodynamics, effects of the spin degrees of freedom, the details of the different time regimes in the dynamics of condensate formation, and how the systems carry angular momentum via vortices and multi-pole shape distortions. There are connections with models of nuclei here.
Fermi systems are also of considerable interest. Because Pauli exclusion limits the phase space available for scattering, the two-body collision rate drops rapidly as the temperature is lowered, and it is difficult to cool and equilibrate a Fermi system in isolation. (In a degenerate Fermi system the Fermi energy is much larger than the temperature. Evaporation carries away highly energetic particles, but this mostly results in lowering the Fermi energy, rather than cooling the system.) However, sympathetic cooling in Bose-Fermi mixtures is possible because the Bose-Fermi collision rate is not limited by the Pauli principle. The fermions cool by losing energy to the bosons, which are in turn cooled by the usual evaporative means. This opens up new possibilities similar to those studied in superfluid3He-4He mixtures but now in a very different regime.
A profound physical problem that the atomic BECs seem well suited to address is that of the dynamics of a macroscopic quantum system approaching an equilibrium state with long-range phase coherence. This physics is important both in connection with the dynamics of the cooling process and for the development of atom lasers ("bosers," see Figure 3.3). Similar questions have been addressed in the condensed-matter literature—for example, in connection with the development of nematic order in liquid crystals quenched from high temperatures. The theory of such ordering kinetics is reasonably well developed. However, the experimental systems studied so far are all well described by a classical, overdamped dynamics; that is, their time evolution consists merely of a frictional descent into the nearest local energy minimum. The theoretical analyses have
Page 148
also all been for purely relaxational models. The dynamics of the atomic BEC systems is clearly not in this regime, as the unitary time evolution of Schrödinger's equation is surely important in the development of macroscopic phase coherence. Experimental and theoretical studies examining these fundamental issues are beginning, and their rapid advancement offers exciting prospects for the future.
Quantum Spin Chains and Ladders
The study of quantum magnetism has experienced a resurgence in the last decade with the synthesis of whole new families of organic and inorganic compounds containing spin-l/2 and spin-1 degrees of freedom. One very important consequence of the discovery of high-temperature superconductors has been progress in the synthesis of oxide compounds having spins arranged in two-dimensional planes, one-dimensional chains, quasi-one-dimensional ladders with both even and odd numbers of legs, and even two-dimensional arrays of intersecting one-dimensional chains. These new systems have fascinating properties and provide an excellent testing ground for theories of strongly correlated electronic systems. The fact that some of these ladders can be doped provides a testing ground for ideas about high-temperature superconductors in a simplified quasi-one-dimensional setting. There may also be even more direct connections because of the existence of quasi-one-dimensional domain wall structures in the so-called "striped phase" of nominally two-dimensional high-Tc materials. Spin-1/2 is the most quantum-mechanical spin length and had previously been available for study only in complicated organometallic compounds. In those materials, the very weak coupling between spins makes the interesting quantum effects only occur at extremely low temperatures.
Paradoxically, magnetism arises from electrostatic not magnetic forces. Magnetic dipole forces are weak and generally detrimental to the creation of magnetic alignment. Instead, it is the Coulomb interaction, combined with the Pauli principle, that can lead to spin alignment and, hence, to magnetism. The overall antisymmetry of the quantum wave function for a pair of electrons requires that the spatial wave function be symmetric for the spin singlet and antisymmetric for the spin triplet. If the spatial wave function is antisymmetric, it vanishes when two electrons are at the same location; thus the probability of close approach is reduced. This in turn reduces the mean Coulomb repulsion. However, this reduction in the potential energy comes at the expense of increased kinetic energy associated with the extra nodes in the spatial wave function. Roughly speaking, if the potential energy term dominates, the system will have a ferromagnetic ground state. If the kinetic energy dominates, the system will have an antiferromagnetic ground state.
Classically, it makes no formal difference to the statistical mechanics whether a local moment system is ferromagnetic or antiferromagnetic (as long as we consider a bipartite lattice so that the antiferromagnetism is not frustrated) or has
Page 149
a large or a small spin angular momentum (say, S = 5/2 or S = 1/2). A classical spin can point in any direction, and its dynamics can be understood in terms of a simple gyroscope precessing under the influence of torques as a result of interactions with its neighbors. This mutual precession leads to the existence of a continuum of spin waves with precession frequencies proportional to the square of the wave vector in ferromagnets and linear in the wave vector for antiferromagnets.
A quantum spin is a very strange and different beast. If its component in a particular direction is measured, it will always be found to be one of a discrete set of only 2S + 1 values: -S, -S + 1, . . . , S - 1, S. This discreteness suggests that quantum magnets could be very different, perhaps having a discrete excitation gap or other properties that depend in detail on the particular value of S.
At the same time, quantum mechanics has another novel feature that opposes this discreteness. Quantum mechanics allows for the possibility of uncertainty as to which state a spin is in. In fact, there exists a continuum of "coherent states" that are linear superpositions of the 2S + 1 discrete basis states. This continuum of possibilities allows the quantum spin to act somewhat classically. Thus, for example, a spin-l/2 can be chosen to be in a linear combination of "up" and "down" that is pointing in some arbitrary transverse direction. This competition between discrete and continuum pictures, which in a sense is analogous to the usual wave-particle duality of quantum mechanics, leads to very rich physics in quantum magnets.
Many spin systems can, to a good approximation, be represented by a quantum Heisenberg model. In spatial dimensions greater than 1, it turns out that for this model, the particular length and discrete nature of the spin is not very crucial, but there is still a major distinction between ferromagnets and antiferromagnets. The ferromagnet has a purely "classical" ground state, in which the spins are fully aligned in some arbitrary direction. The low-lying excited states are spin waves carrying S = 1 and behaving approximately like free bosons whose energy increases quadratically with momentum. The antiferromagnet (whose order parameter is the staggered magnetization) is somewhat different: quantum fluctuations reduce the order parameter below the classical value even at zero temperature; hence, the exact ground state is not known. The low-lying excitations are nevertheless spin waves carrying S = 1 and having an energy linear in the momentum, just as the classical precession frequency is linear rather than quadratic in the wave vector.
These simple pictures break down completely for the case of one-dimensional antiferromagnets, for which quantum fluctuations are especially severe. In particular, there is no long-range order in the staggered magnetization even at zero temperature (the spin-spin correlation functions fall off algebraically at zero temperature and exponentially at finite temperature). For S = 1/2, it turns out that the naive spin wave picture fails because the S = 1 bosonic spin wave "fractionalizes" into
Page 150
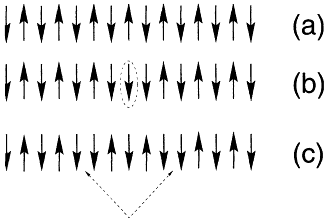
Figure 3.4
Spin fractionalization process in which a DS = 1 spin flip in a
spin chain breaks up into two domain walls each carrying
spin-1/2. (a) Perfectly ordered antiferromagnetic configuration
for a spin-l/2 chain. (b) The circled spin has been flipped.
(c) Adjacent pairs of spins mutually flip producing a pair of
domain walls (indicated by the dashed lines) separating
perfectly ordered antiferromagnetic configurations. These
domain walls ("spinons") are unconfined and free to move
independently.
two independent S = 1/2 objects known as "spinons." A graphic depiction of the fractionalization process is shown in Figure 3.4. The first row shows a perfect antiferromagnetically ordered array of spins. In the second row, angular momentum S = 1 has been added to the array by flipping a single spin in the center. The third row shows the time-evolved state obtained by an angular momentum conserving mutual spin flip of the pair of spins just to the left of the center spin and the pair just to the right. We now see that the original flipped spin has broken up into a pair of "domain walls," which can separate indefinitely because the interior region between the walls is still perfectly ordered antiferromagnetically. It is possible to show that each of these domain-wall defects acts like a quantum particle carrying half of the S = 1 angular momentum of the original spin flip.
An immediate experimental consequence of the spin-wave fractionalization is that there is much more phase space available for spin excitations. An ordinary spin wave has a definite energy associated with each momentum. A pair of spinons, however, can be in many different individual momentum states for a given total momentum. This results in a band of possible energies, rather than a single energy, for a given momentum (see Figure 3.5).
The picture we have just described for one-dimensional spin-l/2 chains applies mutatis mutandis to the case of all odd-half-integer spins (1/2, 3/2, 5/2, . . .). However, the case of integer spin values is radically and surprisingly different. It turns out that integer spin chains described by the Heisenberg model have an
Page 151
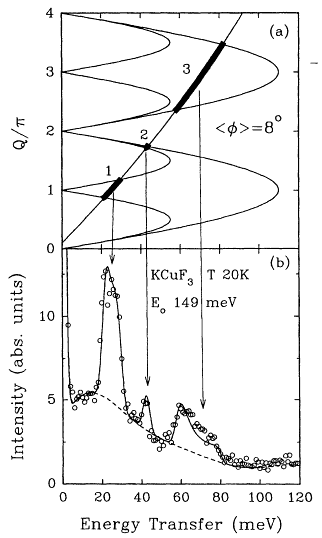
Figure 3.5
Spinon production observed by spin-flip inelastic
neutron scattering. There is much more phase space
available for spinons than for ordinary spin waves.
The curve with period p in the upper panel is the
single spinon dispersion curve. The curve with larger
amplitude and period 2p is the upper bound on the
range of allowed energies for a pair of spinons of total
momentum Q. The parabolic curve in the upper panel
is the kinematically allowed momentum and energy
transfer to the scattered neutrons. The lower panel
shows large peaks in the cross section at energies
correctly predicted by the picture in which a single
flipped spin decays into a pair of independent spinon
excitations. Ordinary spin wave theory would predict
zero intensity in the first and third peaks. [Physical Review
Letters 70, 4003 (1993).]
Page 152
![]()
Figure 3.6
Typical spin configuration in the ground state of the Affleck-Kennedy-Lieb-Tasaki
(AKLT) model. The symbols refer to the z component of the spin at each site. Notice
that, if the zeros are ignored, the state has perfect antiferromagnetic order.
apparently featureless "spin liquid" ground state with an excitation gap and spin correlations that decay exponentially with distance even at zero temperature. The spin degrees of freedom seem to have disappeared because of some "confinement" mechanism.
The origin of the excitation gap is a novel "hidden" topological order not visible in the ordinary spin-spin correlation function. This order is best understood by studying the Affleck-Kennedy-Lieb-Tasaki (AKLT) model, which is closely related to the Heisenberg model but whose ground state is more readily soluble. Figure 3.6 shows a typical configuration (in the Sz basis) of the spins in the ground state of the AKLT model. We see that an up spin can be followed by an arbitrary number of zeros ("sideways spins") but then must be followed by a down spin. That is, if we removed all the zeros, there would be perfect antiferromagnetic order. This novel order is completely invisible to the ordinary, experimentally measured, spin correlation function and can only be detected theoretically using a nonlocal "string order" correlation function that includes a factor of -1 for each of the nonzero spins within the string of spins connecting two sites. The most obvious experimental manifestation of this hidden topological order is that it costs a finite amount of energy to break it; hence, the system has a spin excitation gap.
The origin of the excitation gap can also be understood by examining a different graphic of the AKLT ground state shown in Figure 3.7a. Each S = 1 spin on a site is visualized as being made up of a pair of spin-l/2 particles. These spins are formed into singlet bonds with their neighbors to create a "valence bond solid" as shown. Enforcing the rule that the state be symmetric under interchange of the pair of spins on a site guarantees that they will form a triplet and correctly represent the S = 1 on that site (see Figure 3.8).
Just as in the case of the spin-1/2 chain, it is possible to split a single spin flip with DS = 1 into a pair of spinon excitations each carrying S = 1/2. This is illustrated in Figure 3.7b. Notice now, however, that in order to avoid generating more unpaired spins, the two sites containing the unpaired S = 1/2 spins are connected by a "string" of alternating double bonds and missing bonds. There is a finite "string tension," meaning there is a finite energy cost per unit length to produce this string. Thus, in contrast to the S = 1/2 chains, the spinons are confined (much as quarks are) and the resulting excitation ("meson") has a finite minimum energy cost. It can be shown that this excitation breaks the topological order discussed above. The situation for larger integer spins is similar, but the
Page 153

Figure 3.7
(a) Valence bond solid picture of the same Affleck-Kennedy-Lieb-Tasaki (AKLT)
model ground state shown in Figure 3.6. The dots represent a site that contains a single
spin S = 1. This is viewed as being made up of a pair of spin-l/2 particles, each of which
forms a singlet bond (solid line) with one of its neighbors. (b) An excited state of the
AKLT model. Because sites are viewed as containing two spin-l/2 particles, there must
be either two bonds or one bond and an unpaired spin on each site. Thus there are two
spin-l/2 particles liberated here. The string of alternating double and zero bonds costs a
finite energy per unit length. This "string tension" confines the
spin-l/2 particles together much as quarks are confined.
gap must become exponentially small in order to match onto the gapless classical limit at ![]() .
.
A great deal of theoretical progress has been made in understanding the role of disorder in one-dimensional quantum spin chains for both S = 1/2 and S = 1. The S = 1/2 system develops into a random singlet phase in which there are strong singlet bonds over short distances and arbitrarily weak bonds over arbitrarily long distances. The S = 1 chain is quite different because it is initially gapped and, therefore, stable against weak disorder. For moderately strong disorder, the gap is destroyed, but the topological order remains in a "Griffiths" phase. Thus, paradoxically, the spins that disappeared at low energies in the clean system can be made to reappear by the addition of strong nonmagnetic impurity disorder. This is illustrated in Figure 3.9, which shows a segment of an S = 1 chain cut off from the rest of the chain by a nonmagnetic impurity at each end. The disruption of the valence bond solid ground state liberates a nearly free spin-l/2 at each end of the segment. This is manifested experimentally in the magnetic susceptibility, which becomes algebraic rather than exponential at low temperatures.
There are many open questions still to be addressed. In two and three dimensions there are a rich variety of highly frustrated lattices such as the kagome for which we still lack a complete understanding of the low-energy physics. Debate continues as to whether high-temperature superconductivity occurs because of, or in spite of, antiferromagnetism in the insulating parent compounds. Mixtures of itinerant electrons and local moments occur in heavy fermion, Kondo lattice, and disordered systems near the metal-insulator transition. These continue to be dauntingly complex theoretical and experimental challenges. In addition, the entirely new classes of oxide systems now being synthesized will pro duce fascinating new realizations of ladders, chains, and planes of spins, which will doubtless raise new theoretical and experimental challenges.
Page 154
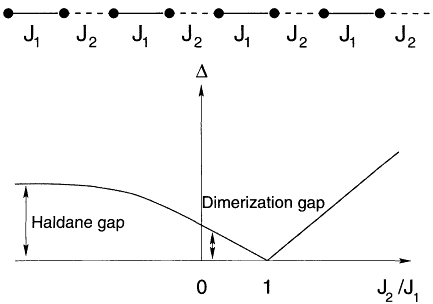
Figure 3.8
There is a connection between the gap seen in S = 1 (and other integer)
chains and the gap seen in dimerized systems. (Upper) Consider the S = 1/2
chain with alternating weak and strong bonds. In the limit J2 = 0, the exact
ground state is a ''valence bond solid" (VBS) of singlets on the J1 bonds.
For J2 nonzero, the bonds begin to fluctuate, but the VBS state still captures
the essential physics, and the gap survives throughout the region ![]() . (Lower)
. (Lower)
The gap persists even as the strength of the weak bond
passes through zero and changes sign to become ferromagnetic.
As these bonds become infinitely ferromagnetic, the associated
pairs of spins become locked into triplet states, and one recovers
the S = 1 spin chain description. Because the gap never closes
during this process, the system does not undergo any phase
transition as the dimerization is varied adiabatically. It follows
that the dimer system has the same type of topological order,
measured by the "string" correlation function, as the S = 1 system
and that the Haldane gap in an S = 1 system is a special limit of the
dimerization gap in an S = 1/2 system. [Reprinted with permission
from S.M. Girvin, "Exotic quantum order in low-dimensional systems,"
Solid State Communications 107, 623 (1998). Copyright © 1998 Elsevier Science.]
![]()
Figure 3.9
Nonmagnetic impurities (denoted by crosses) liberate spin-l/2
degrees of freedom in a gapped spin-1 chain. This follows from
the fact that every site must have either two bonds or one bond
and a free spin. These liberated spins are only weakly coupled to
each other and hence produce low-energy excitations inside the
Haldane gap. They are experimentally observable via their
Curie-like contribution to the susceptibility.
Page 155
The Quantum Hall Effect
The various quantum Hall effects are arguably among the most remarkable many-body phenomena discovered in the second half of the twentieth century, comparable in intellectual import to superconductivity and superfluidity. They are an extremely rich set of phenomena with deep and truly fundamental theoretical implications. The integer effect, whose discovery was awarded the 1985 Nobel Prize (see Table O.1), has revolutionized our understanding of localization and transport in high magnetic fields. The fractional effect, whose discovery and theoretical explanation was awarded the 1998 Nobel Prize (see Table O.1), has yielded new paradigms of fractional charge, spin, and statistics as well as unprecedented order parameters. There are beautiful connections with a variety of different topological and conformal field theories studied as formal models in particle theory, each here made manifest by the twist of an experimental knob. Where else but in condensed-matter physics can an experimentalist change the number of flavors of relativistic chiral fermions, or set the Chern-Simons angle by hand?
Some of the themes discussed above for quantum spin chains reappear here. The gapped-spin liquid with hidden topological order is replaced by a gapped-charge liquid, which also has a novel form of hidden topological order. The concepts of quantum number fractionalization and confinement and deconfinement of quasiparticle excitations also reappear.
Because of the recent technological advances in molecular beam epitaxy and the fabrication of artificial structures, the field continues to advance with new discoveries, even well into the second decade of its existence. Experiments in the field were limited for many years to simple transport measurements that indirectly determine charge gaps. However, recent advances have led to many successful optical, acoustic, microwave, specific heat, and nuclear magnetic resonance (NMR) probes that continue to advance our knowledge as well as raise intriguing new questions.
The quantum Hall effect takes place in a two-dimensional electron gas subjected to a high magnetic field. In essence, it is a result of commensuration between the number of electrons, N, and the number of flux quanta in the applied magnetic field, NF. The electrons undergo a series of condensations into new states with highly nontrivial properties whenever the filling factor n = N/NF takes on simple rational values. The original experimental manifestation of this effect was the observation of an energy gap yielding dissipationless transport (at zero temperature) much like in a superconductor. The Hall conductivity in this dissipationless state is universal, given by sxy = ne2/h independent of microscopic details. As a result of this, it is possible to make a high-precision determination of the fine-structure constant and to realize a highly reproducible quantum-mechanical unit of electrical resistance, now used by standards laboratories around the world to maintain the ohm.
Page 156
The integer quantum Hall effect (IQHE) owes its origin to an excitation gap associated with the discrete kinetic energy levels (Landau levels) in a magnetic field. The fractional quantum Hall effect (FQHE) has its origins in very different physics of strong Coulomb correlations that produce a Mott-insulator-like excitation gap. In some ways, however, this gap is more like that in a superconductor because it is not tied to a periodic lattice potential. This permits uniform charge flow of the incompressible electron liquid and, hence, a quantized Hall conductivity.
The microscopic correlations leading to the excitation gap are captured in a revolutionary wave function, developed by R.B. Laughlin, that describes an incompressible quantum liquid. The charged quasiparticle excitations in this system are ''anyons" carrying fractional statistics, intermediate between bosons and fermions, and fractional charge. This sharp fractional charge, which despite its bizarre nature has always been on solid theoretical ground, has recently been observed directly in two different ways. The first is an equilibrium thermodynamic measurement using an ultrasensitive electrometer built from quantum dots (see Figure 3.10). The second is a dynamical measurement using exquisitely sensitive detection of the shot noise for quasiparticles tunneling across a quantum Hall device.
Quantum mechanics allows for the possibility of fractional average charge in both a trivial way and a highly nontrivial way. As an example of the former, consider a system of three protons, arranged in an equilateral triangle, and one electron tunneling among their 1S atomic bound states. The electronic ground state is a symmetric linear superposition of the quantum amplitudes for being in each of the three different 1S orbitals. In this trivial case, the mean electron number for a given orbital is 1/3. This is a result of statistical fluctuations, however, because a measurement will yield electron number 0 two-thirds of the time and electron number 1 one-third of the time. These fluctuations occur on a very slow timescale and are associated with the fact that the electronic spectrum consists of three very nearly degenerate states corresponding to the different orthogonal combinations of the three atomic orbitals.
The n = 1/3 quantum Hall effect has charge-1/3 quasiparticles, but it is profoundly different from the trivial scenario just described. An electron added to a n = 1/3 system breaks up into three charge-1/3 quasiparticles. If the locations of the quasiparticles are pinned by, say, an impurity potential, the excitation gap still remains robust and the resulting ground state is nondegenerate. This means that a quasiparticle is not a place (like the proton above), where an extra electron spends one-third of its time. The lack of degeneracy implies that the location of the quasiparticle completely specifies the state of the system; that is, it implies that these are fundamental elementary particles with charge 1/3. Because there is a finite gap, this charge is a sharp quantum observable that does not fluctuate (for frequencies below the gap scale).
To understand this better, imagine that you are citizen of Flatland, living in
Page 157
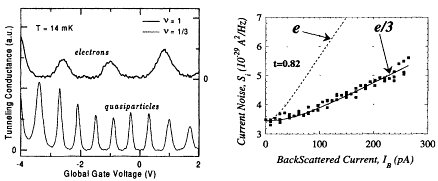
Figure 3.10
(Left) Variation of the conductance for tunneling through a quantum dot }
as a function of bias voltage on the dot. The oscillations indicate the
discrete charging of the dot under quasi-thermodynamic equilibrium
conditions. The period of the oscillations for the n = 1/3 quantum Hall
plateau is three times smaller than for the n = 1 plateau, indicating that
the quasiparticle charge is one-third that of an electron. (Right)
Absolute shot noise for currents tunneling through a n = 1/3 Hall fluid.
The deviation from linearity at low currents is the crossover from shot
noise to thermal Nyquist noise. Both the intensity of the noise and the
location of the crossover from shot noise to Nyquist noise are in
quantitative agreement with the quasiparticle charge being e* = 1/3.
The dashed line shows the predicted shot noise if the current were
carried by objects with charge e instead of e/3. [Right: Reprinted with
permission from R. De-Picciotto, M. Reznikov, M. Heiblum, V. Umansky,
G. Bunin, and D. Mahalu, "Direct observation of a fractional
charge," Nature 389, 163 (1997). Copyright © 1997 Nature.]
the cold world of a two-dimensional electron gas in a high magnetic field. Flatland cosmologists have theorized that the charged particles seen drifting around are topological defects left over from the Big Chill at the beginning of the universe. Flatland particle theorists decide that the apparently featureless vacuum in which everyone lives each day is actually a roiling sea, filled with strange but invisible objects that have precisely three times the charge of one of these quasi particles. To study this possibility, a Flatland high-energy particle accelerator is constructed that can reach the unprecedented energy scale of 10 K. On smashing together three charged particles, it is found that they do indeed temporarily coalesce into an object with the bizarre property of having integer charge. It is decided to name this short-lived object "the electron."
The message here is that the charge of the quasiparticles is sharp to the observers so long as the gap energy scale is considered large. If the gap were 10 GeV instead of 10 K, we (living at room temperature) would have no trouble accepting the concept of fractional charge.
Page 158
Composite Particles
It is a peculiarity of two dimensions that the n = 1/3 vacuum represented by the Laughlin wave function can be viewed in more than one way in terms of composite particles. One way is to make a singular gauge transformation that attaches three quanta of magnetic flux to each electron. This induces an Aharonov-Bohm phase of 3p when two particles are interchanged. The physics will therefore remain invariant if we change the particle statistics from fermion to boson to cancel this phase change. At n = 1/3 there are three flux quanta from the externally applied uniform magnetic field for each particle. Thus, if we make a mean-field approximation in which the flux quanta attached to the particles are smeared out into a uniform field, they will precisely cancel the external field, leaving a theory of composite bosons in zero (mean) magnetic field, as illustrated schematically in Figure 3.11. The condensate wave function of these bosons defines a hidden off-diagonal long-range order not visible in the ordinary correla-
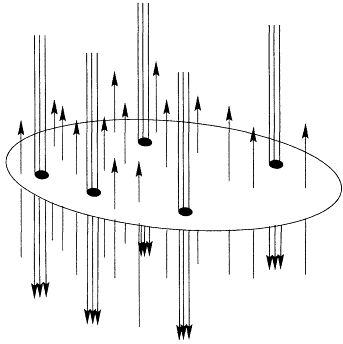
Figure 3.11
Illustration of the condensation of composite bosons in the n = 1/3
fractional quantum Hall effect. The three flux quanta attached to the
electrons convert them into bosons moving in zero average field.
Vortices in the condensate are the Laughlin quasiparticles
carrying charge ±1/3.
Page 159
tion functions of the original electron variables. (There are deep analogies here with the hidden string order in quantum spin chains discussed previously.)
The natural excitations in a bosonic condensate are (Goldstone mode) phonons and vortices. The analogs here ("magnetophonons") have recently been observed directly in Raman scattering. Vortices in two dimensions normally cost a logarithmically divergent amount of energy and are confined in neutral pairs at low temperatures. In the FQHE, however, something peculiar happens. Because each composite boson carries three flux quanta, binding one-third of a charge to the vortex is equivalent to binding one quantum of flux to the vortex. Just as in a type-II superconductor, this quantized flux screens out the currents at large distances and removes the divergence in the energy. Thus in this picture, the Laughlin quasiparticles are topological defects, and the same mechanism that gives them fractional charge also deconfines them. By analogy with type-II superconductors, the magnetophonon acquires a mass gap, which was predicted theoretically and has been observed experimentally.
An alternative picture of the n = 1/3 vacuum can be developed by attaching two rather than three flux quanta to each particle. These composite objects remain fermions and see a mean magnetic field of one flux quantum per particle, as illustrated schematically in Figure 3.12. Thus the n = 1/3 FQHE is mapped onto the IQHE at neff = 1. The Laughlin quasiparticles become additional composite fermions added to the next Landau level. In this formulation the off-diagonal long-range order remains hidden, but there are two significant advantages. First, accurate variational wave functions for various hierarchical quantum Hall states at different rational filling fractions can be written down explicitly and studied numerically with relative ease. Second, the special case of n = 1/2 is naturally described as composite fermions in zero mean magnetic field. The characteristic Fermi surface wave vector 2kF of these composite fermions has been observed in surface acoustic wave attenuation experiments. If the mean field picture is taken literally, then moving slightly away from n = 1/2 puts the composite fermions in a weak magnetic field that should cause the quasiparticles to follow curved trajectories. Remarkably, this too has been observed experimentally.
It should be emphasized that experiments to date have all dealt with the kinematics of the composite fermions and the associated length scales, not their dynamics and the associated frequency scales. Hence, there is no unambiguous evidence for long-lived Fermi liquid-like quasiparticles above a sharply defined Fermi surface, as opposed to well-defined length scales at the Fermi surface. There is great theoretical interest currently in trying to understand the nature of fluctuations around the mean-field solution and their effect on the composite fermions. Considerable progress has been made, but many questions still remain to be definitively settled.
Page 160
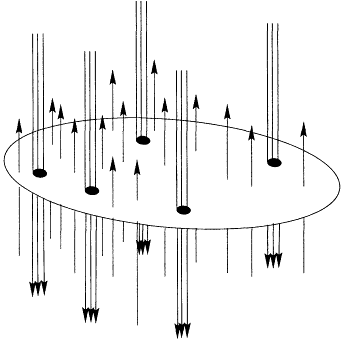
Figure 3.12
Illustration of the formation of composite fermions in the n = 1/3
fractional quantum Hall effect. The two flux quanta attached to
the electrons turn them into fermions moving in an average field
corresponding to the n = 1 integer quantum Hall effect. A
Laughlin quasiparticle is represented by a composite fermion in
the next Landau level.
Edge States
At low energies, the bulk of an FQHE system appears as a featureless vacuum with an excitation gap; however, very unusual gapless modes exist at the edges. These are shape distortions that preserve the area of the incompressible fluid. In a certain sense, the quantized-edge density fluctuations can be viewed as a gas of Laughlin quasiparticles liberated from the bulk gap.
Because these objects carry fractional charge and statistics in the bulk, they do not form an ordinary Fermi liquid at the edge. Instead, they constitute a nearly ideal realization of a chiral Luttinger liquid. The edge modes are chiral because they propagate in only a single direction, controlled by the direction of E × B drift in the edge-confinement potential. The density of states for tunneling an ordinary electron into a Luttinger liquid vanishes with a power-law singularity at low energies because of an orthogonality catastrophe that results from the fact that the electron must break up into fractionally charged quasiparticles. Recent progress
Page 161
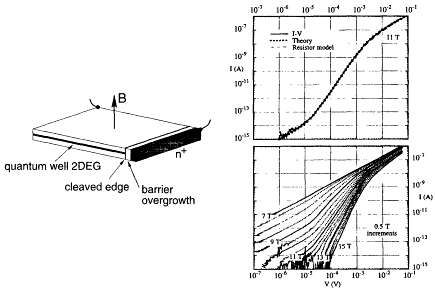
Figure 3.13
(Left) Schematic of a device produced by cleaved-edge
overgrowth methods to measure tunneling into the edge
of a two-dimensional electron gas. (Right) Nonlinear
current-voltage response for tunneling an electron into
a fractional quantum Hall effect edge state. Because the
electron must break up into three fractionally charged
quasiparticles, there is an orthogonality catastrophe
that leads to a power-law density of states. The flattening
at low currents is caused by the finite temperature.
[Physical Review Letters 77, 2538 (1996).]
in sample fabrication using cleaved-edge overgrowth techniques has made it possible to observe the resulting singularity experimentally in the tunneling current-voltage characteristic, as shown in Figure 3.13.
The various power-law correlations in a Luttinger liquid are characterized by a critical exponent g, which normally is continuously variable, depending on the details of the particle interactions. The value of g is therefore nonuniversal and can only be roughly estimated theoretically. According to current theory, one of the most important features of the chiral Luttinger liquids realized at the edge of FQHE systems is that g is universal, dependent only on the quantized value of the Hall conductivity in the bulk and independent of all details of the electron interactions. In particular, this makes the temperature and voltage dependence of the tunneling current have a power-law form that is universal and independent of all microscopic details. The theory works extremely well on the 1/3-quantized Hall plateau, but the unexpectedly smooth variation of the exponent with magnetic field away from the plateau shown in Figure 3.13 is not yet understood.
Page 162
Magnetic Order of Spins and Pseudospins
At certain filling factors (n = 1 in particular), quantum Hall systems exhibit spontaneous magnetic order. For reasons peculiar to the band structure of the gallium arsenide host semiconductor, the external magnetic field couples exceptionally strongly to the orbital motion, giving a large Landau level splitting, and exceptionally weakly to the spin degrees of freedom, giving a very small Zeeman gap. The resulting low-energy spin degrees of freedom of this ferromagnet have some rather novel properties, which have recently begun to be probed by NMR, specific heat, and other measurements.
Because the lowest spin state of the lowest Landau is completely filled at n = 1, the only way to add charge is with reversed spin. However, because the exchange energy is large and prefers locally parallel spins, and because the Zeeman energy is small, it is cheaper to partially turn over several spins, forming the topological spin texture shown in Figure 3.14. Because this is an itinerant magnet with a quantized Hall conductivity, it turns out that this texture (called a skyrmion by analogy with the corresponding object in the Skyrme model of nuclear physics) accommodates precisely one extra unit of charge. NMR Knight shift and other measurements have confirmed the prediction that each charge added or removed from the n = 1 state flips over several spins—from 4 to 30, depending on the pressure. In the presence of skyrmions, the ferromagnetic order
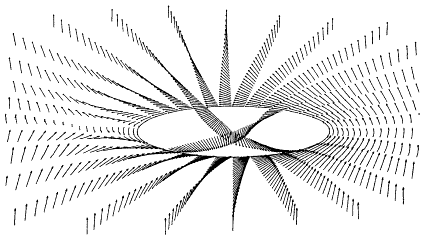
Figure 3.14
Skyrmion spin texture in a quantum Hall ferromagnet. Note that
the spins are all up at infinity but down at the origin. At
intermediate distances they have a vortex-like configuration.
Because of the quantized Hall conductivity, these objects
carry quantized charge. [Reprinted with permission from
S.M. Girvin, "Exotic quantum order in low-dimensional
systems," Solid State Communications 107, 623 (1998).
Copyright © 1998 Elsevier Science.]
Page 163
is no longer collinear, leading to the possibility of additional low-energy spin wave modes that remain gapless even in the presence of the Zeeman field (somewhat analogous to an antiferromagnet). These low-frequency spin fluctuations have been indirectly observed through a dramatic enhancement of the nuclear spin relaxation rate 1//T1. In fact, under some conditions T1 becomes so short that the nuclei come into thermal equilibrium with the lattice via interactions with the inversion layer electrons. This has recently been observed experimentally through an enormous enhancement of the specific heat by more than five orders of magnitude (see Figure 3.15).
Spin is not the only internal degree of freedom that can spontaneously order. There has been considerable recent progress experimentally in overcoming technical difficulties in the molecular beam epitaxy fabrication of high-quality multiple-well systems. It is now possible, for example, to make a pair of identical electron gases in quantum wells separated by a distance of about 100 Å—comparable to the electron spacing within a single quantum well. Under these conditions strong interlayer correlations can be expected. One of the peculiarities of quantum mechanics is that it is possible, even in the absence of tunneling between the layers, for the electrons to be in a coherent state in which their layer index is uncertain. To understand the implications of this, we can define a pseudospin that is up if the electron is in the first layer and down if it is in the second. Spontaneous interlayer coherence corresponds to spontaneous pseudospin magnetization lying in the x-y plane (corresponding to a coherent mixture of pseudospin up and down). If the total filling factor for the two layers is v = 1, then the Coulomb exchange energy will strongly favor this magnetic order, just as it does for real spins. This long-range transverse order has been observed experimentally through the strong response of the system to a weak magnetic field, applied in the plane of the electron gases, in the presence of weak tunneling between the layers. Very recent work indicates that a two-layer quantum Hall system at filling factor v = 2 may even allow for an antiferromagnetic or a canted spin phase, further demonstrating the complexity and richness of the magnetic phase diagrams of quantum Hall systems.
Another interesting aspect of two-layer systems is that, despite their extreme proximity, it is possible to make separate electrical contact to each layer and perform drag experiments in which current in one layer induces a voltage in the other as a result of Coulomb or phonon-mediated interactions.
The many-body physics of two-layer systems can also be found in wide single-well systems with the two (nearly degenerate) lowest electric sub-band states playing the role of the pseudospin degrees of freedom.
Stacking together many quantum wells gives an artificial three-dimensional structure analogous to certain organic Bechgaard salts in which the quantum Hall effect has been observed. Interest has been growing recently in the bulk and edge ("surface") states of such three-dimensional systems and in the nature of possible Anderson localization transitions.
Page 164
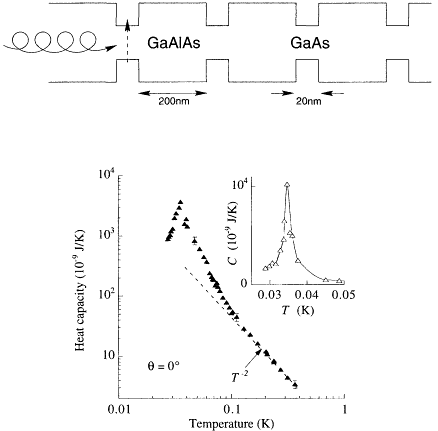
Figure 3.15
Even in a sample with many quantum wells, there are not enough nuclei in the 20-nm-thick wells to do an ordinary nuclear magnetic resonance (NMR) experiment. The technique of optically pumped NMR therefore had to be developed [Barrett et al., Physical Review Letters 74, 5112 (1995); Tycko et al., Science 268, 1460 (1995)]. (Upper) Circularly polarized light above the gallium arsenide (GaAs) band gap but below the band gap of gallium aluminum arsenide (GaAlAs) is absorbed only in the quantum wells. The angular momentum of the photons is transferred to the orbital motion of excited electrons and then, via the spin-orbit interaction, to the electron spins. Finally, the hyperfine interaction transfers the polarization to the nuclei in the quantum wells. This polarization enhancement allows the NMR signal to each detectable levels for samples with as few as 10 wells. NMR experiments clearly demonstrate the existence of skyrmions—collective excitations with charge ±e and large-spin S. These objects enhance the nuclear relaxation rate, bringing T1 down from many hours to about 20 seconds. (Lower) With the nuclei in thermal equilibrium, the specific heat is enhanced by many orders of magnitude, rising from picojoules to microjoules per kelvin. [Physical Review Letters 76, 4584 (1996) and 79, 1718 (1997).]
Page 165
Although the quantum Hall effect is extremely well understood at this point, there remain some important mysteries yet to be resolved. In the IQHE, the main question continues to be the nature of the delocalization transition in which the Hall conductivity jumps from one quantized value to the next. The general scenario by which this happens is well understood; it is almost certain that there exists a critical point near the center of each Landau level at which the localization length diverges, and numerical estimates of the critical exponent agree well with experiment—in selected samples, at least. It is not understood at present, however, why generically there are often deviations from the expected scaling behavior (although the answer probably has to do with macroscopic inhomogeneities). One problem only just beginning to be addressed is the possible relevance of Coulomb interactions to the transition. In addition, despite valiant efforts, there does not yet exist a simple quantum field theory for this transition from which we can analytically compute the critical exponent. Finally, there remains an interesting set of puzzles about what happens at weak magnetic fields as Landau level mixing becomes strong and direct transitions apparently occur from quantum Hall effect states to insulating states.
In general, the ordering that produces the hierarchy of fractionally quantized states is very well understood. The most interesting remaining problem is to understand the physics of the v = 1/2 state, which in the composite fermion picture is a Fermi liquid-like state with zero mean magnetic field. The nature and effect of fluctuations around the mean field still need to be better understood.
The theory of quantum Hall edge states has successfully made detailed predictions of the observed temperature and voltage dependence of the tunneling current-voltage characteristics of the v = 1/3 fractional plateau edge. One unexpected experimental discovery, however, has been that the edge-tunneling density of states has a power law-form over a wide range of magnetic fields, not just on the plateaus. Furthermore, as shown in Figure 3.15, the exponent of the power law varies continuously and linearly with magnetic field and seems quite insensitive to whether the bulk of the sample is in a quantized Hall state or not. Current theory predicts that the exponent should be quantized, just as the Hall conductivity is, and should vary discontinuously with magnetic field.
Another significant question involves the sharp peak in the specific heat shown in Figure 3.15. The large linear region in the plot is explained quantitatively by the Schottky anomaly of the nuclei in the quantum wells. The extra peak is known to involve the additional nuclei in the barriers between the quantum wells, but the mechanism that gives rise to a sharp feature is not understood at present. It may be related in some way to the freezing of the skyrmions.
Page 166
Summary
The committee has detailed here just a small sampling of the wide variety of novel quantum effects that have been explored successfully in the past decade. Some of the major accomplishments are listed below:
• The discovery of high-temperature superconductivity and identification of the symmetry of the order parameter and elucidation of novel vortex fluctuations.
• Discovery of quantum phase transitions in two dimensional systems such as antiferromagnets in high-temperature superconductors, the superconductor-insulator phase transition in metal films, the metal-insulator transition in two-dimensional electron gases, and a wide variety of novel quantum Hall transitions.
• Observation of Bose-Einstein condensation and macroscopic coherence effects in atom traps.
• Synthesis of new families of spin-1 and spin-l/2 quantum magnets with a variety of novel geometries, progress in understanding dynamics in disordered one-dimensional magnets, and the development of giant and colossal magnetore-sistance materials.
• Numerous new discoveries in quantum Hall physics including direct observation of the fractional charge of quantum Hall effect quasiparticles, composite particles, edge-state modes, Raman observation of the fractional quantum Hall effect neutral excitation gap, discovery of drag and spontaneous coherence in double-layer systems, and NMR and nuclear specific heat anomalies due to skyrmions.
• Mesoscopic device physics observations of conductance quantization in electron wave guides, parity effects in superconducting grains, and Andreev reflection in disordered systems.
Future Directions And Research Priorities
The novel discoveries of the last decade have raised many new questions and issues that require further exploration both theoretically and experimentally:
• New tools and paradigms for studying the interplay between interactions and disorder in quantum systems would shed light on phenomena like the recently discovered metal-insulator transition in two-dimensional electron gases.
• Carbon nanotubes are likely to present a great opportunity for study of novel electronic properties.
• Many of the remarkable quantum effects discovered in the last decade have been observable only at relatively low temperatures. Can quantum energy scales be boosted so that, for example, room-temperature mesoscopic and single-electron devices can be constructed?
Page 167
• Can we develop practical theoretical tools to describe real-time dynamics and nonlinear response of interacting quantum systems as well as their electronic structure?
• Can we develop general principles to guide us in the study of modern materials that are vastly more complex than materials of the past?
• What is the physics of the normal and condensed states of high-temperature superconductors? Can we synthesize room-temperature superconductors and overcome practical materials difficulties?
• Finally, if the past is any guide, we will be faced with completely unexpected and surprising quantum phenomena as new materials are synthesized. What new techniques will have to be developed to deal with these surprises?
































