Cloud Cavitation Phenomena
C.Brennen, T.Colonius, Y.-C.Wang, A.Preston (California Institute of Technology, USA)
ABSTRACT
This paper describes investigations of the dynamics and acoustics of clouds of cavitation bubbles. Recent experimental and computational findings show that the collapse of clouds of cavitating bubbles can involve the formation of bubbly shock waves and that the focussing of these shock waves is responsible for the enhanced noise and damage in cloud cavitation. The recent experiments and computations of Reisman et al. (1) complement the work begun by Mørch and Kedrinskii and their co-workers (2,3,4) and demonstrate that the very large impulsive pressures generated in bubbly cloud cavitation are caused by shock waves generated by the collapse mechanics of the bubbly cavitating mixture. Here we describe computational investigations conducted to explore these and other phenomena in greater detail as part of an attempt to find ways of ameliorating the most destructive effects associated with cloud cavitation.
Understanding such bubbly flow and shock wave processes is important because these flow structures propagate the noise and produce the impulsive loads on nearby solid surfaces in a cavitating flow. How these shocks are formed and propagate in the much more complex cloud geometry associated with cavitating foils, propeller or pump blades is presently not clear. However, the computational investigations reveal some specific mechanisms which may be active in the dynamics and acoustics of these more complex flows.
1. NOMENCLATURE
|
a |
Amplitude of plate motion |
|
A |
Radius of the bubble cloud |
|
A0 |
Initial radius of the bubble cloud |
|
Cp |
|
|
Cpmin |
Minimum pressure coefficient |
|
D |
Reference body size |
|
k |
Polytropic constant for gas inside the bubble |
|
p |
Fluid pressure (Pa) |
|
p0 |
Upstream reference pressure (Pa) |
|
pυ |
Vapor pressure |
|
R |
Bubble radius |
|
R0 |
Initial radius of the bubble |
|
t |
Time |
|
T |
Period of plate oscillation |
|
U |
Reference velocity of the flow (m/s) |
|
α |
Void fraction of the bubbly mixture |
|
α0 |
Initial void fraction of bubbly mixture |
|
αc |
Critical void fraction |
|
β |
|
|
ρ |
Density of the liquid |
|
σ |
|
2. INTRODUCTION
In many flows of practical interest, clouds of cavitation bubbles are periodically formed and then collapse. This temporal periodicity may occur naturally as a result of the shedding of bubble-filled vortices or it may be the response to a periodic disturbance imposed on the flow. Common examples of imposed fluctuations are the interaction between rotor and stator blades in a pump or turbine and the interaction between a ship’s propeller and the non-uniform wake created by the hull. When the density of cavitation events increases in space or time and bubbles therefore begin to interact, a whole new set of phenomena may be manifest
both in the dynamics and the acoustics. In many of these cases the coherent collapse of the cloud of bubbles can cause a substantial increase in the radiated noise and potential for damage. Much recent interest has focused on the dynamics and acoustics of finite clouds of cavitation bubbles because of these very destructive effects (see, for example, Knapp (5), Bark and van Berlekom (6), Soyama et al. (7)). The purpose of the computational investigations outlined in this paper is to explore the various phenomena which can occur in the dynamics anfd acoustics of these bubbly cavitating flow and, where possible, to compare these with experimental observations.
1. Some Recent Experiments on Cloud Cavitation
Numerous investigators (for example, Knapp (5), Wade and Acosta (8), Bark and van Berlekom (6), Shen and Peterson (9,10), Bark (11), Franc and Michel (12), Hart et al. (13), Kubota et al. (14,15), Le et al. (16), de Lange et al. (17), Kawanami et al. (18)) have studied the complicated flow patterns involved in the production and collapse of cloud cavitation on a hydrofoil. The basic features of the cyclic process of cloud formation and collapse (whether on a stationary or oscillating foil) are as follows. The growth phase usually involves the expansion of a single attached cavity, at the end of which a re-entrant jet penetrates the cavity from the closure region. This penetration breaks the cavity into a bubbly cloud which collapses as it is convected downstream.
The radiated noise all occurs during this bubbly part of the cycle. It consists of pressure pulses of very short duration and large magnitude. The pulses have been observed and measured by a number of investigators including Bark (11), Bark and van Berlekom (6), Le et al. (16), Shen and Peterson (9,10), McKenney and Brennen (19) and Reisman et al. (20). More recently, Reisman et al. (1) have made measurements of the impulsive pressures on the suction surface of a hydrofoil (within the cloud cavitation), have simultaneously measured the radiated pulses and have correlated these pressure traces with images from high-speed movies. Very large pressure pulses were recorded by the surface transducers, with typical magnitudes as large as 10bar and durations of the order of 10−4s. These help to explain the enhanced noise and cavitation damage associated with cloud cavitation. For example, the large impulsive surface loadings due to these pulses could be responsible for the foil damage reported by Morgan (21), who observed propeller blade trailing edges bent away from the suction surface and toward the pressure surface.
Reisman et al. (1) also correlated high-speed movies of the clouds with the pressure measurements and found that the pressure pulses recorded (both on the foil surface and in the far field) were associated with specific structures (more precisely, the dynamics of specific structures) which are visible in the movies. Indeed, it appears that several types of propagating structures (shock waves) are formed in a collapsing cloud and dictate the dynamics and acoustics of collapse. One type of shock wave structure is associated with the coherent collapse of a well-defined bubble cloud which separates from the rear of the cavitation zone and is convected downstream. This type of structure causes the largest impulsive pressures and radiated noise. The pulses it produces are termed global pulses since they are recorded almost simultaneously by all transducers. The high-speed motion pictures showed that the cavitation cloud undergoes a rapid and coherent collapse and that these collapses generate the global pulses. It was noted that such cloud collapses do not involve large and rapid changes in the volume of the cloud. Rather, they involve rapid and propagating changes in the void fraction distribution within the cloud.
Unexpectedly, two other types of structures were observed. Typically, the pulses produced by these structures were registered by only one transducer and these events were therefore termed local pulses. They are recorded when an ephemeral, localized and transient low void fraction structure forms in the bubbly cavitating cloud and happens to pass over the face of the transducer. While these local events are smaller and therefore produce less radiated noise, the pressure pulse magnitudes are almost as large as those produced by the global events. How and why these low void fraction structures (shock waves) form in the flow is not at all clear.
Finally, we note that injection of air into the cavitation on the suction surface can substantially reduce the magnitude of the pressure pulses produced (Ukon (22), Arndt et al. (23), Reisman et al. (24)). However Reisman et al. (25) have shown that the bubbly shock wave structures still occur; but with the additional air content in the bubbles, the pressure pulse magnitudes are greatly reduced.
2. On Calculations of Cloud Cavitation
The experimental and practical observations of cloud cavitation exemplified by the preceding discussion have generated much interest in modelling the dynamics and acoustics of these flows. These efforts began with the work of van Wijngaarden (26) who first attempted to model the behavior of a collapsing layer of bubbly fluid next to a solid wall. The essence of his approach was to couple conventional continuity and momentum equations for the compressible mixture to a Rayleigh-Plesset equation for the bubble dynamics (see, for example, Brennen (27)) which would provide the neccessary relation connecting the local pressure with the bubble size and therefore the local mixture density. This is the basis for most of the computational investigations which have been carried out subsequently. Later investigators explored numerical methods which incorporate the individual bubbles (Chahine (28)) and continuum models which, for example, analyzed the behavior of shock waves in a bubbly liquid (Noordzij and van Wijngaarden (29), Kameda and Matsumoto (30)) and identified the natural frequencies of spherical clouds of bubbles (d’Agostino and Brennen (31)). Indeed the literature on the linearized dynamics of clouds of bubbles has grown rapidly (see, for example, d’Agostino et al. (32,33), Omta (34), Prosperetti (35)). However, apart from some weakly non-linear analyses (Kumar and Brennen (36,37,38)) only a few papers have addressed the highly non-linear processes which are an inevitable consequence of the non-linearities in the Rayleigh-Plesset equation and are most evident during the collapse of a cloud of bubbles. Chahine and Duraiswami (39) have conducted numerical simulations using a number of discrete bubbles and demonstrated how the bubbles on the periphery of the cloud develop inwardly directed re-entrant jets. However, most clouds contain many thousands of bubbles and it therefore is advantageous to examine the non-linear behavior of continuum models.
Another perspective on the subject of collapsing clouds was that introduced by Mørch and Kedrinskii and their co-workers (Mørch (2,3), Hanson et al. (4)). They surmised that the collapse of a cloud of bubbles involves the formation and inward propagation of a shock wave and that the geometric focusing of this shock at the center of cloud creates the enhancement of the noise and damage potential associated with cloud collapse. We begin the review of computational efforts by describing studies of the dynamics of a spherical cloud of bubbles, a simple example which illustrates these processes of shock wave formation, propagation and focussing.
3. Computations: [1] Dynamics of a Spherical Cloud
Wang and Brennen (40,41,42) (see also Reisman et al. (1)) used a mixture model comprising the continuity, momentum and Rayleigh-Plesset equations (for specifics see, for example, d’Agostino et al. (31,32,33)) to study the non-linear growth and collapse of a spherical cloud of bubbles. A finite cloud of nuclei is subjected to an episode of low pressure which causes the cloud to cavitate; the pressure then returns to the original level causing the cloud to collapse. Wang and Brennen used the computational model to study the various cloud dynamics and acoustics exhibited in various parametric regimes. Key parameters are the cavitation number, σ, which characterizes the the initial pressure level, the magnitude of the low pressure episode characterized by a minimum pressure coefficient, Cpmin, and by a duration, D/U. The initial radius and void fraction of the cloud are denoted by A0 and α0 respectively and the initial radius of the bubbles within the cloud is denoted by R0.
This parametric exploration revealed that the dynamics and acoustics depended in an important way on the “cloud interaction parameter”, β, defined as
(1)
Note that, while the initial void fraction, α0, is very small, the ratio, A0/R0, may be very large so that β could be small or large compared with unity. Earlier linear and weakly nonlinear studies of cloud dynamics (d’Agostino & Brennen (31,32,33), Kumar & Brennen (36,37,38)) showed that the cloud natural frequency is strongly dependent on this parameter. If β is small, the natural frequency of the cloud is close to that of the individual bubbles in the cloud. In other words, the bubbles in the cloud tend to behave as individual units in an infinite fluid and the bubble/bubble interaction effects are minor. On the other hand bubble interaction effects dominate when the value of β is greater than order one. Then the collective oscillation of bubbles in the cloud results in a cloud natural frequency which is lower than the natural frequency of individual bubbles.
In all of the computations of Wang and Bren-
nen, the bubbles in the interior of the cloud are shielded by the outer shell of bubbles and grow to a smaller maximum size. This shielding effect is typical of the bubble/bubble interaction phenomenon in cavitating cloud dynamics (d’Agostino & Brennen (31,33); Omta (34); Smereka & Banerjee (48); Chahine & Duraiswami (39)).
The non-linear computations showed that when β≫1, spherical cloud collapse began on the cloud surface and propagated inwards as a collapse front. As a result of the bubble collapse within this front, a large pressure pulse or shock wave becomes an integral part of the propagating collapse front. The structure of this shock is very similar to those in the bubbly flows investigated by Noordij and van Wijngaarden (29) and other investigators (see, for example, Brennen (27), Kameda and Matsumoto (30)); the shock is comprised of a series of rebounds and secondary collapses. The locations with small bubble size represent regions of low void fraction and higher pressure due to the local bubble collapse. The magnitude of the pressure pulse grows due to geometric focussing as the front progresses inward and reaches very large magnitudes when it reaches the center of the cloud. At this instant a very large, positive pressure pulse is radiated away from the cloud into the far-field; all the earlier or later radiated noise is almost insignificant by comparison. Another characteristic of the collapse is the relatively small change which occurs in the cloud radius, A. The essential collapse process is unlike that of a single bubble and involves the propagation of void fraction waves within the cloud rather than radical volumetric change.
In contrast, Wang and Brennen found that the dynamics and acoustics when β≪1 were quite different. Then collapse began with the bubbles at the cloud center and the collapse front propagated outward producing a much more benign process and much reduced radiated noise.
[Parenthetically we note that all of the preceding computations were done with a cloud consisting of a uniform dispersion of identical bubbles. Real clouds will have a distribution of bubble sizes. Wang (43) has recently developed a computational methodology to deal with this more complex circumstance. Moreover, he observes some significant differences in the dynamics and acoustics of these non-monodisperse clouds.]
When compared with the experimental observations of Reisman et al. (1) and others, the results of the computations of Wang and Brennen reveal many parallels. First note that the value of β in a real flow will increase as the cavitation number is decreased and more and more nuclei are activated. Thus the critical value of β of about unity may be manifest in practice as a critical cavitation number below which cloud cavitation begins.
Secondly, we note that shock waves characterized by large, positive pressure pulses and zones of low void fraction may form during the cloud collapse process. They will then propagate through the cloud and can grow to very large magnitudes due to geometric focussing. Such structures were observed by Reisman et al. (1).
Finally we note that there may be important implications for model testing in water tunnels. Since α0 and R0 tend to be similar at the model and full scales but A0 could be radically different, it follows that the model tests might be conducted at much smaller values of β than pertain at full scale. Consequently there is a real risk that violent cloud cavitation could occur at full scale and not at the model scale.
4. Computations: [2] Harmonic Cascading
We now shift attention to a different set of computational investigations in order to discuss two other non-linear acoustic phenomena which have been identified from the calculations of cloud dynamics. Both of these emerge from calculations of the response of a liquid layer (laced with cavitation nuclei or bubbles but at small void fraction) to the vibration of an infinite flat plate in a direction normal to its surface. Kumar and Brennen (36,38) present both the linear and a weakly nonlinear solution to this problem utilizing the same set of model equations described above. While a multitude of non-linear effects occur in the weakly non-linear solution (in which terms quadratic in the oscillation amplitude are retained but all higher order terms are neglected) we highlight just one here because of its practical significance. This emerges from calculations using typical size distributions of bubbles; each size, of course, has its own single bubble natural frequency with the larger number of smaller bubbles having a much higher natural frequency than the fewer, larger bubbles.
Kumar and Brennen (37) identify a phenomenon they call harmonic cascading. In this process the larger bubbles, responding mostly to oscillations
at their relatively low natural frequency, produce higher harmonics due to non-linear effects. These higher frequencies in turn excite a much larger number of smaller bubbles because that higher harmonic corresponds to the basic natural frequency of those smaller bubbles. The measured spectra of cavitation reported by Mellen (44) and by Blake et al. (45) contain peaks which may well be due to harmonic cascading. In any case, it seems clear that non-linear effects combined with a typical bubble number distribution provide a mechanism for the cascading of acoustic energy from low frequencies to high frequencies where the attenuation is, in turn, more effective in damping the noise.
5. Computations: [3] Acoustic Saturation
A second notable phenomenon emerges from fully non-linear calculations of the same physical problem of a liquid layer and will be referred to as acoustic saturation. In this case a distribution of bubble sizes is not essential and so results are presented for nuclei of just one uniform equilibrium size. Colonius et al. (46) and Brennen et al. (47) demonstrate what happens as the amplitude of the plate oscillation is increased from the linear regime up to the highly non-linear regime in which true cavitation bubble collapses occur. The bubbles next to the wall behave as expected as the amplitude is increased as illustrated in figure 1. This shows the typical development of a Rayleigh-Plesset solution with increasing amplitude. We note that in this and the other results presented in this section, that the bubble damping has been adjusted to a value which is consistent with the experimentally observed spatial attenuation of acoustic waves in bubbly liquids. This also produces a more realistic number of rebounds than the much smaller value used in the nozzle calculations of the next section (see Colonius et al. (46)).
More unexpected is the behaviour of the bubbles further away from the plate. At low amplitudes the sinusoidal pressure oscillations produced by the oscillating plate simply propagate away with an amplitude directly proportional to the amplitude of motion of the plate. But, as non-linear effects begin to become significant, the radiated signal is attenuated relative to the expected linear magnitude and, eventually, reaches an asymptotic value. This phenomenon is illustrated in figures 2, 3 and 5. Figure 2 presents the typical pressure signals occurring at a distance from the plate and the
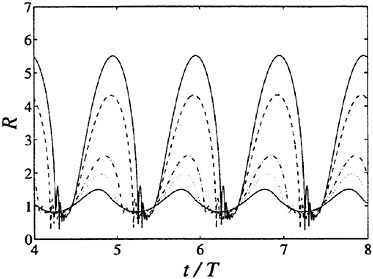
Figure 1. Typical radii/time histories for the bubbles at the surface of the plate for plate velocity amplitudes, a, equal to 0.05 (solid line), 0.075 (dots), 0.1 (dash-dot), 0.2 (dashes) and 0.3 (solid line). The initial void fraction and cavitation number are respectively 0.01 and 0.475 and other parameters are given in Colonius et al. (46).
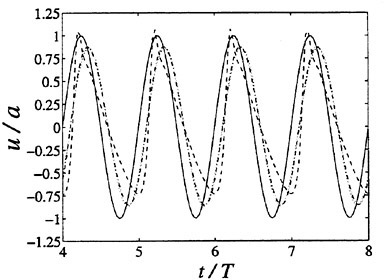
Figure 2. The fluid velocity (normalized by the velocity amplitude at the plate surface) at the plate surface (solid line) and at a distance of 400 initial bubble radii into the fluid as a function of reduced time for plate velocity amplitudes, a, equal to 0.0001 (dots), 0.001 (dash-dot) and 0.01 (dashes) initial bubble radii. The initial void fraction and cavitation number are respectively 0.01 and 0.475 and other parameters are given in Colonius et al. (46).
essentially linear behavior at low amplitudes (the vertical coordinate is the instantaneous fluid velocity normalized by the magnitude of the wall velocity oscillations). On the other hand, figure 3 presents the typical behaviour at large amplitudes; the non-normalized signals at a distance from the plate are almost independent of the plate amplitude. Thus further increase in the plate oscillation amplitude produces no change in the radiated noise. This
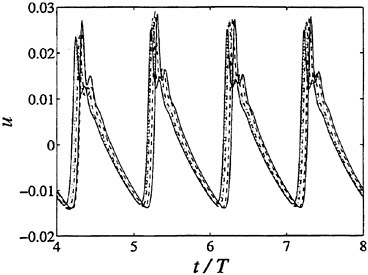
is, in part, caused by the formation of a highly active layer adjacent to the plate where the bubbles grow large enough that their momentary natural frequency is no longer large compared to the plate oscillation frequency. Thus acoustic energy is trapped and dissipated in this layer near the plate (see also Smereka and Banerjee (48)). Increasing the plate amplitude simply results in greater dissipation and in no increase in the radiated noise. The nature of the layer for this particular case is further illustrated in figure 4. Note that the layer decreases in thickness from about 200 initial bubble radii at an amplitude of a=0.025 to 120 initial bubble radii at a=0.3. The figure clearly shows how the response increases with amplitude within the layer but is independent of ampltitude outside the layer.
The acoustic saturation phenomenon in this case is summarized in figure 5 which plots the magnitude of the bubble radius oscillations some distance from the plate as a function of the amplitude of the plate oscillations. This clearly demonstrates the acoustic saturation phenomenon. It could be a contributing factor to the frequently made experimental observation that, as the pressure in a flow is decreased and the cavitation increases, the noise often plateaus out and may even decrease after a certain point.
Finally, we remark that the description of the acoustic saturation phenomenon given above is pertinent to the sub-resonant behaviour manifest when the plate oscillation frequency is substan
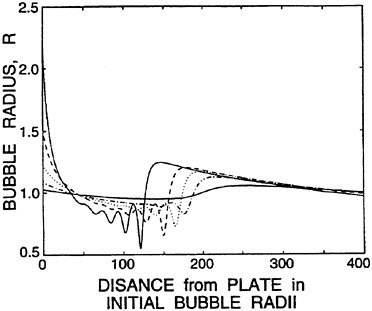
Figure 4. Snapshots at one moment in time (t/T=76) of the variation in bubble radius with distance from the plate for the same case as figure 1.

Figure 5. The amplitude of the bubble radius oscillations for the computations of figures 2 and 3 as a function of the plate amplitude, a. The circles are the bubble radius amplitudes at the wall and the crosses are the bubble radius amplitudes at a distance from the wall of 400 initial bubble radii.
tially smaller than the natural frequency of the individual bubbles in the fluid. Other non-linear effects are exhibited when the plate frequency approaches or exceeds the bubble natural frequency. Then, as anticipated by Smereka and Banerjee (48) (see also Lauterborn and Koch (49)) and confirmed by Brennen et al. (47), the non-linear effects produce a cascade of bifurcations leading, eventually, to a chaotic response of the bubbly fluid. This super-resonant regime is not, however, of great practical interest for, other than in the context of ultrasonic cavitation, it is uncommon to en-
counter circumstances in which the imposed excitation reaches such a high frequency.
6. Computations: [4] Steady Flow through a Nozzle
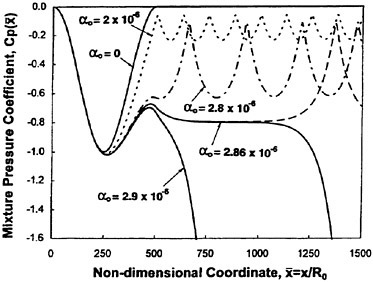
All of the above computations involve bubbly liquids which are not flowing in the mean. It is more challenging to devise numerical methodologies for cases in which the bubbly liquid is flowing and particularly difficult when dealing with a two- or three-dimensional flow. In this section we examine a case of a one-dimensional cavitating flow, namely that through a nozzle. When the same approach is applied to such a bubbly cavitating flow the solutions exhibit several interesting features which may provide insight into more complex two and three dimensional flows such as those over hydrofoils or propeller blades. Using the same basic equations previously discussed, namely a continuity equation, an inviscid momentum equation and the Rayleigh-Plesset equation to connect the local pressure with the local mixture density or bubble size, Wang and Brennen (50) present results for the one-dimensional, bubbly, frictionless cavitating flow through a convergent/divergent nozzle. The following typical flow will illustrate the phenomena manifest in the nozzle computations. A bubbly liquid, composed of air bubbles (k=1.4) in water at 20°C (liquid density, 1000 kg/m, surface tension, 0.073 N/m), flows through a nozzle whose total length is 500 initial upstream bubble radii. The minimum or throat pressure coefficient for incompressible flow is −1.0 and the present example is for an upstream cavitation number, σ, of 0.8. The Reynolds number is also important since it determines the damping of the bubble oscillations (see Wang and Brennen (50)). It could be chosen, as suggested by Chapman and Plesset (51), so as to accommodate other, non-viscous contributions to the bubble damping. Five different upstream void fractions, α0, of the order of 10−6 are used in the computation and the results are shown in figures 6, 7, 8 and 9. Figures 6 and 7 respectively present the axial variations of the mixture velocity and the mixture pressure coefficient in this typical calculation.
The case of α0=0 corresponds to the incompressible pure liquid flow. It is notable that even for an upstream void fraction as small as 2×10−6, the characteristics of the flow are radically changed from the case without bubbles. Radial pulsation of bubbles results in the downstream fluctuations of
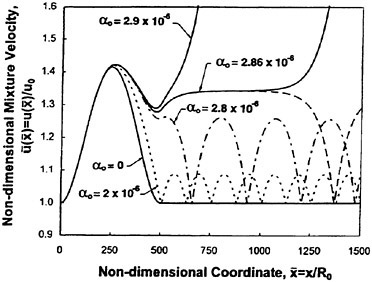
Figure 6. The non-dimensional mixture velocity distribution as a function of the non-dimensional position in the flow for five different upstream void fractions, α0, from Wang and Brennen (50). The dimensionless length of the nozzle is 500 with the throat located at 250; the cavitation number, σ=0.8, the throat pressure coefficient for incompressible flow is −1.0 and other parameters are as given in the original reference. Note that, for this case, the critical value of the void fraction is 2.862×10−6.
the flow. The amplitude of the velocity fluctuation is 10% of that of the incompressible flow in this case. As α0 increases further, the amplitude as well as the wavelength of the fluctuations increase. However, the velocity does eventually return to the upstream value. In other words, the flow is still “quasi-statically stable.” However, as α0 increases to a critical value, αc (αc≈2.862×10−6 in the present example), a bifurcation occurs. Wang and Brennen (50) show that a critical state is reached downstream of the nozzle when the instantaneous bubble radius, Rc, reaches a value given approxi-
mately by

(2)
where R0 is the radius of the bubbles (assumed monodisperse) in the upstream flow. This implies that when the instantaneous bubble size exceeds Rc, the flow becomes unstable and flashes. In the context of an experiment in which only the upstream void fraction, α0, is increased while the other parameters are held fixed, this implies that the flow will flash at a critical value of the upstream void fraction, αc, which in the present example yields (σ/2αc)1/3≈51. Figure 9 demonstrates the veracity of the above expression for Rc/R0.
The flow becomes quasi-statically unstable and flashes to vapor if the radius of the cavitating bubbles is greater than Rc. In this circumstance, the growth of bubbles increases the mixture velocity due to mass conservation of the flow. The velocity increase then causes the mixture pressure to decrease according to the momentum equation. The decrease of the pressure is fed back to the Rayleigh-Plesset equation and results in further bubble growth. In this case the velocity and void fraction of the mixture increase and the pressure coefficient of the flow decreases significantly below the upstream values and the flow flashes to vapor. On the other hand, if the bubbles do not grow beyond Rc, the flow is quasi-statically stable and is characterized by large amplitude spatial fluctuations downstream of the throat.
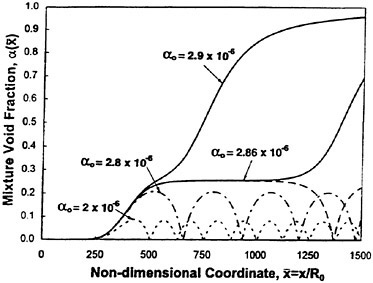
Figure 8 illustrates the void fraction distribution in the flow. When the flow becomes quasi-statically unstable, the bubble void fraction quickly
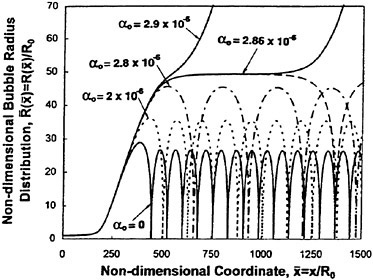
approaches unity. This means that the flow is flashing to vapor. However, it should be cautioned that when α becomes large, the present model loses validity since it is limited to flows with small void fraction. Figure 9 indicates the non-dimensional bubble radius distribution in the flow. Due to time lag during the bubble growth phase, bubbles reach the maximum size downstream of the throat. With increase in the upstream void fraction, the maximum size of the bubbles increases and is shifted further downstream. The bubbles grow without bound after reaching a critical radius, Rc, at which flashing begins.
Note from figure 7, that the downstream mixture pressure does not return to the upstream value except in the case of the pure liquid flow. Since viscous effects are neglected in the global mixture flow and the only dissipation present is that in the Rayleigh-Plesset equation representing bubble dynamic damping, the pressure and energy losses are caused by the radial motion of bubbles and are therefore “cavitation losses.”
In addition to the two different flow regimes, another important feature in the quasi-statically stable flow is the typical frequency associated with the downstream periodicity. This “ringing” will result in acoustic radiation at frequencies corresponding to this wavelength. How this ring frequency relates to the upstream flow condition remains to be studied.
In summary, it is found that the nonlinear bubble dynamics coupled with the equations of motion of the mixture strongly affect the structure of the
flow even for very small bubble populations. Two different flow regimes, distinguished by the parameter Rc=R0(σ/2αc)1/3, are revealed in the steady state solutions. The results also imply that there exists a domain of pressure drops and void fractions for which no steady state flow solution exists. It remains to be determined whether those conditions lead to the unsteady, oscillatory cavitating flows which are observed in practice.
7. Computations: [5] Two and Three-dimensional Cavitating Bubbly Flows
It is more challenging to devise numerical methodologies for two and three-dimensional bubbly cavitating flows. In this regard we should mention several recent efforts to develop approximate methods for two-dimensional flows. Both Song (52) and Merkle and Feng (53) have modified compressible gas dynamic codes, introducing some artificial algebraic equation of state to relate the mixture density to the pressure. While these results are of some qualitative value they omit the essential bubble dynamic effects which would result from a more appropriate differential “equation of state” such as implied by the Rayleigh-Plesset equation. Perhaps Kubota et al. (15) come closest to a true two-dimensional methodology; however, by not permitting the bubbles to collapse below the original nuclei size, they exclude the formation of the large pressure perturbations and shock waves which are such an important part of cloud cavitation.
8. Computations: [5] Example: Encounter of Low Pressure Pulse with a Cylindrical Cloud
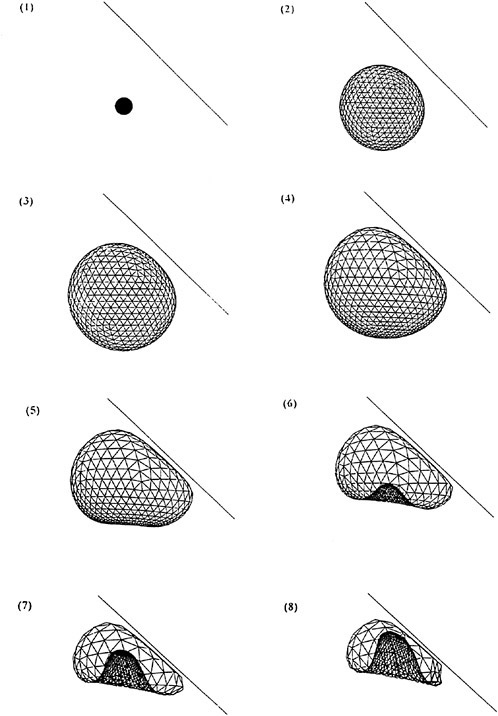
We illustrate some of the multidimensional phenomena by presenting preliminary computational results for a particularly simple two-dimensional calculation, namely the response of a cylindrical bubble cloud to an incident, planar pressure pulse (specifically a low pressure pulse) travelling through the liquid (which is assigned some compressibilty so the progress of the wave may be recorded). The initial conditions are shown in figure 10. In this particular example the initial bubble cloud has a Gaussian radial distribution of void fraction reaching a maximum of 0.5% at the center of the cloud. The gray scale of the right-hand image depicts the void fraction distribution while that in the left-hand image shows the liquid density and, by implication, the pressure and scattered waves. The incident wave moves from left to right in the sequence of images, figures 10 through 15, and is diffracted and scattered by the low sound speed inside the cloud. The pressure in the wave is low enough to cause cavitation and the bubbles within the cloud grow to nearly 100 times their original volume before collapsing violently. The bubbles on the left-hand side of the cloud grow first and collapse first, the latter process initiating a collapse front which propagates from left to right through the cloud. Sufficient damping is included in the Rayleigh-Plesset equation so that only a few bubble rebounds occur, but these are evident in the scattered sound (see figure 15).
9. Concluding Comments
In this paper we have summarized some of the recent advances in our understanding of bubbly cloud cavitation. It is becoming clear that effects of the interaction between bubbles may be crucially important especially when they give rise to the phenomenon called cloud cavitation. Calculations of the growth and collapse of a spherical cloud of cavitating bubbles show that when the cloud interaction parameter (β) is large enough, collapse occurs first on the surface of the cloud. The inward propagating collapse front becomes a bubbly shock wave which grows in magnitude due to geometric focussing. Very large pressures and radiated impulses occur when the shock reaches the center of the cloud.
Of course, actual clouds are far from spherical. And, even in a homogeneous medium, gas-dynamic shock focussing can be quite complex and involves significant non-linear effects (see, for example, Sturtevant and Kulkarny (54)). Nevertheless, it seems evident that once collapse is initiated on the surface of a cloud, the propagating shock will focus and produce large local pressure pulses and radiated acoustic pulses. It is not, however, clear exactly what form the foci might take in the highly non-uniform, three-dimensional bubbly environment of a cavitation cloud on a hydrofoil, for example.
Experiments with hydrofoils experiencing cloud cavitation have shown that very large pressure pulses occur within the cloud and are radiated away from it during the collapse process. Within the cloud, these pulses can have magnitudes as large as 10bar and durations of the order of 10−4s. This suggests a new perspective on cavitation damage and noise in flows which involve large collec-
Figures 9 through 15. A series of snapshots in time of a planar pressure pulse impinging on a cylindrical cloud. The image on the right shows the fluid density (the white circle is the initial location of the cloud) while that on the right shows the void fraction distribution. Note that the image on the right is a close-up view compared with that on the left.

Figure 10. Initial conditions with low pressure pulse (vertical) moving from left to right and about to impinge on the cylindrical bubble cloud.

Figure 11. Expansion (or cavitation) of cloud.
tions of cavitation bubbles with a sufficiently large void fraction (or, more specifically, a large enough β) so that the bubbles interact and collapse coherently. This view maintains that the cavitation noise and damage is generated by the formation and propagation of bubbly shock waves within the collapsing cloud. The experiments reveal several specific shock wave structures. One of these is the mechanism by which the large coherent collapse of a finite cloud of bubbles occurs. A more unexpected result was the discovery of more localized bubbly shock waves propagating within the bubbly mixture in several forms, as crescent-shaped regions and as leading edge structures. These seem to occur when the behavior of the cloud is less coherent. They produce surface loadings which are within an order of magnitude of the more coherent events and could also be responsible for cavitation damage. However, because they are more localized, the radiated noise they produce is much smaller than that due to global events.
The phenomena described are expected to be important features in a wide range of cavitating flows. However, the analytical results clearly suggest that the phenomena may depend strongly on the cloud interaction parameter, β. If this is the case, some very important scaling effects may occur. It is relatively easy to envision a situation in which the β value for some small scale model experiments is too small for cloud effects to be important but in which the prototype would be operating at a much larger β due to the larger cloud size, A0 (assuming the

Figure 12. Scattered wave. Collapse beginning on left side of cloud.

Figure 13. Collapse front moves through cloud from left to right.

Figure 14. Collapse produces second radiated pulse.
void fractions and bubble sizes are comparable). Under these circumstances, the model would not manifest the large cloud cavitation effects which could occur in the prototype.
Computational methods will play a key role in these developing studies. Not only will such methods be needed for the prediction of these flows in practical applications (particularly to predict the noise and damage potential) but they are almost essential in building our understanding of simpler

Figure 15. Cloud returning to original shape and size.
key problems and laboratory investigations. Here we have described a progression of computational investigations which began with the calculations by Wang and Brennen (40,41,42) of the behaviour of a spherical cloud of bubbles subjected to a low pressure episode. Wang and Brennen (50) then extended this one-dimensional methodology to investigate the steady flow of a bubbly, cavitating mixture through a convergent/divergent nozzle. Under certain parametric conditions, the results are seen to model the dynamics of flashing within the nozzle. Moreover, it is clear from these steady flow studies that there are certain conditions in which no steady state solution exists and it is speculated that the flow under those conditions may be inherently unstable. Of course, it has frequently been experimentally observed that cavitating nozzle flows can become unstable and oscillate violently. Finally, we have also described recent efforts (Colonius et al. (46)) to extend the code to two and three space dimensions.
In conclusion, these recent investigations provide new insights into the dynamics and acoustics both of individual cavitation bubbles and of clouds of bubbles. In turn, these insights suggest new ways of modifying and possibly ameliorating cavitation noise and damage.
10. Acknowledgements
Our profound thanks to the Office of Naval Research for the support which it provided under contract N00014–97–1–0002 and to the technical monitor Edwin Rood who sponsored much of the research described herein.
REFERENCES
1. Reisman, G.E., Wang, Y.-C. and Brennen, C.E., “Observations of shock waves in cloud cavitation,” J. Fluid Mech., 1998, Vol. 355, pp. 255–283.
2. Mørch, K.A., “On the collapse of cavity cluster in flow cavitation,” Proc. First Int. Conf. on Cavitation and Inhomogenieties in Underwater Acoustics, Springer Series in Electrophysics, 1980, Vol. 4, pp. 95–100.
3. Mørch, K.A., “Cavity cluster dynamics and cavitation erosion,” Proc. ASME Cavitation and Polyphase Flow Forum, 1981, pp. 1–10.
4. Hanson, I., Kedrinskii, V.K. and Mørch, K.A., “On the dynamics of cavity clusters,” J. Appl. Phys., 1981, Vol. 15, pp. 1725–1734.
5. Knapp, R.T., “Recent investigation on the mechanics of cavitation and erosion damage,” Trans. ASME, 1955, pp. 1045–1054.
6. Bark, G. and van Berlekom, W.B., “Experimental investigations of cavitation noise,” Proc. 12th ONR Symp. on Naval Hydrodynamics, 1978, pp. 470–493.
7. Soyama, H., Kato, H. and Oba, R., “Cavitation observations of severely erosive vortex cavitation arising in a centrifugal pump,” Proc. Third I. Mech. E. Int. Conf. on Cavitation, 1992, pp. 103–110.
8. Wade, R.B. and Acosta, A.J., “Experimental observations on the flow past a plano-convex hydrofoil,” ASME J. Basic Eng., 1966, Vol. 88, pp. 273–283.
9. Shen, Y. and Peterson, F.B., “Unsteady cavitation on an oscillating hydrofoil,” Proc. 12th ONR Symp. on Naval Hydrodynamics, 1978, pp. 362–384.
10. Shen, Y. and Peterson, F.B., “The influence of hydrofoil oscillation on boundary layer transition and cavitation noise,” Proc. 13th ONR Symp. on Naval Hydrodynamics, 1980, pp. 221–241.
11. Bark, G., “Developments of distortions in sheet cavitation on hydrofoils,” Proc. ASME Int. Symp. on Jets and Cavities, 1985, pp. 215–225.
12. Franc, J.P. and Michel, J.M., “Unsteady attached cavitation on an oscillating hydrofoil,” J. Fluid Mech., 1988, Vol. 193, pp. 171–189.
13. Hart, D.P., Brennen, C.E. and Acosta, A.J., “Observations of cavitation on a three dimensional oscillating hydrofoil,” ASME Cavitation and Multiphase Flow Forum, 1990, FED-Vol. 98, pp. 49–52.
14. Kubota, A., Kato, H., Yamaguchi, H. and Maeda, M., “Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling,” ASME J. Fluids Eng., 1989, Vol. 111, pp. 204–210.
15. Kubota, A., Kato, H. and Yamaguchi, H., “A new modelling of cavitating flows—a numerical study of unsteady cavitation on a hydrofoil section,” J. Fluid Mech., 1992, Vol. 240, pp. 59–96.
16. Le, Q., Franc, J.M. and Michel, J.M., “Partial cavities: global behaviour and mean pressure distribution,” ASME J. Fluids Eng., 1993, Vol. 115, pp. 243–248.
17. de Lange, D.F., de Bruin, G.J. and van Wijngaarden, L., “On the mechanism of cloud cavitation—experiment and modelling,” Proc. 2nd Int. Symp. on Cavitation, Tokyo, 1994, pp. 45–49.
18. Kawanami, Y., Kato, H., Yamaguchi, H., Tagaya, Y. and Tanimura, M., “Mechanism and control of cloud cavitation,” Proc. ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, 1996, FED-Vol. 236, pp. 329–336.
19. McKenney, E.A. and Brennen, C.E., “On the dynamics and acoustics of cloud cavitation on an oscillating hydrofoil”, Proc. ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, 1994, FED-Vol. 190, pp. 195–202.
20. Reisman, G.E., McKenney, E.A. and Brennen, C.E., “Cloud cavitation on an oscillating hydrofoil,” Proc. 20th ONR Symp. on Naval Hydrodynamics, 1994, pp. 78–89.
21. Morgan, W.B., personal communication, 1995.
22. Ukon, Y., “Cavitation characteristics of a finite swept wing and cavitation noise reduction due to air injection,” Proc. Int. Symp. on Propeller and Cavitation, 1986, pp. 383–390.
23. Arndt, R.E.A., Ellis, C.R. and Paul, S., “Preliminary investigation of the use of air injection to mitigate cavitation erosion,” Proc. ASME Symp. on Bubble Noise and Cavitation Erosion in Fluid Systems, 1993, FED-Vol. 176, pp. 105–116.
24. Reisman, G.E. and Brennen, C.E., “Shock wave measurements in cloud cavitation,” Proc. 21st Int. Symp. on Shock Waves, 1997, Paper 1570.
25. Reisman, G.E., Duttweiler, M.E. and Brennen, C.E., “Effect of air injection on the cloud cavitation of a hydrofoil,” Proc. ASME Fluids Eng. Div. Summer Meeting, 1997, Paper No. FEDSM97–3249.
26. van Wijngaarden, L., “On the collective collapse of a large number of gas bubbles in water,” Proc. 11th Int. Conf. Appl. Mech., Springer-Verlag, Berlin, 1964, pp. 854–861.
27. Brennen, C.E., “Cavitation and bubble dynamics,”, 1995, Oxford University Press.
28. Chahine, G.L. “Cloud cavitation theory,” Proc. 14th ONR Symp. on Naval Hydrodynamics, 1982, p. 51.
29. Noordij, L. and van Wijngaarden, L., “Relaxation effects, caused by relative motion, on shock waves in gas-bubble/liquid mixtures,” J. Fluid Mech., 1974, Vol. 66, pp. 115–143.
30. Kameda, M. and Matsumoto, Υ., “Structure of shock waves in a liquid containing gas bubbles,” Proc. IUTAM Symp. on Waves in Liquid/Gas and Liquid/Vapour Two-Phase Systems, 1995, pp. 117–126.
31. d’Agostino, L. and Brennen, C.E., “On the acoustical dynamics of bubble clouds,” ASME Cavitation and Multiphase Flow Forum, 1983, pp. 72–75.
32. d’Agostino, L. and Brennen, C.E., “Acoustical absorption and scattering cross-sections of spherical bubble clouds,” J. Acoust. Soc. of Amer., 1988, Vol. 84, No. 6, pp. 2126–2134.
33. d’Agostino, L. and Brennen, C.E., “Linearized dynamics of spherical bubble clouds,” J. Fluid Mech., 1989, Vol. 199, pp. 155–176.
34. Omta, R., “Oscillations of a cloud of bubbles of small and not so small amplitude,” J. Acoust. Soc. Am., 1987, Vol. 82, pp. 1018–1033.
35. Prosperetti, A., “Bubble-related ambient noise in the ocean,” J. Acoust. Soc. Am., 1988, Vol. 84, pp. 1042–1054.
36. Kumar, S. and Brennen, C.E., “Non-linear effects in the dynamics of clouds of bubbles,” J. Acoust. Soc. Am., 1991, Vol. 89, pp. 707–714.
37. Kumar, S. and Brennen, C.E., “Harmonic cascading in bubble clouds,” Proc. Int. Symp. on Propulsors and Cavitation, Hamburg, 1992, pp. 171–179.
38. Kumar, S. and Brennen, C.E., “Some nonlinear interactive effects in bubbly cavitating clouds,” J. Fluid Mech., 1993, Vol. 253, pp. 565–591.
39. Chahine, G.L. and Duraiswami, R., “Dynamical interactions in a multibubble cloud,” ASME J. Fluids Eng., 1992, Vol. 114, pp. 680–686.
40. Wang, Y.-C. and Brennen, C.E., “Shock wave development in the collapse of a cloud of bubbles,” ASME Cavitation and Multiphase Flow Forum, 1994.
41. Wang, Y.-C. and Brennen, C.E., “The noise generated by the collapse of a cloud of cavitation bubbles,” ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, 1995, FED-Vol. 226, pp. 17–29.
42. Wang, Y.-C. and Brennen, C.E., “Shock wave and noise in the collapse of a cloud of cavitation bubbles,” Proc. 20th Int. Symp. on Shock Waves, Pasadena, 1995, pp. 1213–1218.
43. Wang, Y.-C., “Effects of nuclei size distribution on the dynamics of a spherical cloud of cavitation bubbles,” Proc. ASME Fluids Eng. Div. Summer Meeting, Washington, D.C., 1998.
44. Mellen, R.H., “Ultrasonic spectrum of cavitation noise in water,” J. Acoust. Soc. Am., 1954, Vol. 26, No. 3, pp. 356–360.
45. Blake, W.K., Wolpert, M.J. and Geib, F.E., “Cavitation noise and inception as influenced by boundary-layer development on a hydrofoil,” J. Fluid Mech., 1977, Vol. 80, pp. 617–640.
46. Colonius, T., Brennen, C.E. and d’Auria, F., “Computation of shock waves in cavitating flows,” Proc. ASME Fluids Eng. Div. Summer Meeting, Washington, D.C., 1998.
47. Brennen, C.E., Colonius, T., d’Auria, F. and Preston, A., “Computing shock waves in cloud cavitation,” Proc. CAV98 Third Int. Symp. on Cavitation, Grenoble, France, 1998.
48. Smereka, P. and Banerjee, S., “The dynamics of periodically driven bubble clouds,” Phys. Fluids, 1988, Vol. 31, pp. 3519–3531.
49. Lauterborn, W. and Koch, A., “Holographic observation of period-doubled and chaotic bubble oscillations in acoustic cavitation,” Phys. Rev. A, 1987, Vol. 35, No. 4, pp. 1974–1976.
50. Wang, Y.-C. and Brennen, C.E., “One-dimensional bubbly cavitating flows through a converging-diverging nozzle,” ASME J. Fluids Eng., 1998, Vol. 120, pp. 166–170.
51. Chapman, R.B. and Plesset, M.S., “Thermal effects in the free oscillation of gas bubbles,” ASME J. Basic Eng., 1971, Vol. 93, pp. 373–376.
52. Song, C.S., “Direct numerical simulation of sheet cavitation and cloud cavitation,” Presentation to 1997 ONR Workshop on the Dynamics of Bubbly Flows, San Diego.
53. Merkle, C. and Feng, J., “Dynamics of sheet cavitation,” Presentation to 1998 ONR Workshop on Free Surface Turbulence and Bubbly Flows, Pasadena, CA.
54. Sturtevant, B. and Kulkarny, V.J., “The focusing of weak shock waves,” J. Fluid Mech., 1996, Vol. 73, pp. 651–680.
55. Blake, W.K., “Mechanics of flow-induced sound and vibration”, 1986, Academic Press, New York.
56. Blake, W.K., “Propeller cavitation noise. The problems of scaling and prediction,” Proc. Int. ASME Symp. on Cavitation and Multiphase Flow Noise, 1986, pp. 89–99.
57. Sturtevant, B. and Kulkarny, V.J., “The focusing of weak shock waves,” J. Fluid Mech., 1996, Vol. 73, pp. 651–680.
DISCUSSION
J.Duncan
University of Maryland, USA
The authors are to be commended for elucidating a number of interesting dynamic effects with a relatively simple model. How would you expect your spherical cloud results to change if you included liquid compressibility in the calculations? Of particular interest to me are the effects of shocks, created by collapsing bubbles, on neighboring bubbles.
AUTHORS’ REPLY
I thank Professor Duncan for his kind remarks. In response to his question, the liquid compressibility plays a quite minor role in the mechanics since the bubble “compressibility” is so much greater. In past analysis (see d’Agostino and Brennen, JFM, 1989, Vol. 199, pp. 155–176) we have included this effect for completeness and demonstrated the effect to be small. In the present analyses it was omitted for simplicity.
On the Flow Structure and Turbulence in the Closure Region of Attached Cavitation
Y.Zhang, S.Gopalan, J.Katz (Johns Hopkins University, USA)
Abstract
PIV measurements are used to resolve the flow structure at the closure region and downstream of sheet cavitation. This paper presents data includes instantaneous and averaged velocity, vorticity and turbulence when the ambient pressure is reduced slightly below the cavitation inception level. Two series of tests performed at the same velocity and pressure, i.e. at essentially the same hydrodynamic conditions, but at different temperatures, 35°C and 45°C focus on the effect of small changes in the cavitation index (4.69 vs. 4.41). The results show that the collapse of vapor cavities in the closure region is a primary mechanism of vorticity production. When the cavity is thin there is no reverse flow downstream and below the cavitation, i.e. a re-entrant flow does not occur. Instead, the cavities shrink as the vapor condenses creating in the process a variety of highly irregular vapor patches. The averaged velocity distributions demonstrate that the unsteady cavity collapse in the closure area involves substantial increases in turbulence, momentum and displacement thickness. A small decrease in cavitation indices increases the size of the cavity slightly, but has a major impact on the turbulence level and momentum deficit in the boundary layer downstream.
Introduction
At early phases of sheet cavitation, when the cavitation index is just below the inception level, the cavity is typically thin and has a glossy leading edge with either a blunt front or a series of sharp thin “fingers”. Their occurrence depends on the surface roughness (Zhang et al., 1998). The development of attached cavitation from nuclei in flows with laminar separation was demonstrated first by Arakeri and Acosta (1973) and later confirmed by Gates and Acosta (1978) and Katz (1984). They showed that “band type cavitation” occurred as free stream bubbles were entrained into the separated region through the reattachment zone, where they were pushed upstream by the reverse flow. Within the relative quiescent flow of the separated region the bubbles grew slowly. These observations provided for the first time a clue on the process of sheet formation. However, they were also puzzling, since sheet cavitation occurs on surfaces without laminar separation. Thus, the basic mechanism of sheet formation in attached flows remains unanswered.
If the cavitation nucleus is a free stream bubble, it is typically separated from the solid boundary by some liquid. The attachment of this bubble to the surface and the mechanism that prevents the bubbles from being swept away, as demonstrated by Ceccio and Brennen (1991) are unresolved issues. The process must involve favorable conditions that may include the local pressure distribution, boundary layer thickness, super-saturation (supply of gas) and local surface imperfection. The latter creates localized flow separation with the associated quiescent region, where bubbles may grow without being swept away. Note also that the presence of a cavitation bubble near the surface changes the local flow structure, and may cause local boundary layer separation. It is well established that the size and shape of surface roughness affect the conditions for inception (Arndt et al., 1979). The origin of cavitation can also be a surface nucleus (Harvey et al., 1947; Acosta and Hamaguchi, 1967; Peterson, 1968).
Predictions of the length of the cavity have been mostly based on potential flow analysis and empirical data (Tulin, 1953, 1955, 1964, Tulin and Hsu, 1980; Wu, 1962—see a summary by Wu, 1972). Recently, Laberteaux and Ceccio (1998) compared measured results to theoretical predictions and shown major discrepancies. Of the past efforts to model the flow one should mention the singularity
methods of Furness and Hutton (1975) and the Bubble Two Phase Flow model developed by Kubota et al. (1992). The latter followed earlier experiments (Kubota et al., 1989) that demonstrated that the flow rolled up to large vortex structures as the cavity surface became unstable. Their model predicted the unsteady shedding process at the closure region of the cavity. However, the origin of the vorticity causing the rollup was still in the boundary layer upstream of the cavitation and the rollup occurred as the shear layer became unstable. As will be shown in this paper, although some vorticity is generated in the boundary layer upstream, the dominant origin of the vorticity downstream of the cavitation is the collapse of cavities in the closure region.
As the pressure is reduced further the cavitating region grows and becomes increasingly unstable. Portions of the cavity are being shed in larger sections and at lower frequencies to form large bubbly clouds. This shedding process involves substantial changes to the length of the attached sheet. The development, motion and collapse of the cloud is the most destructive form of cavitation. We have very little data or even qualitative understanding of the breakdown of the cavitation and the bubble size distribution within the cloud. Surface pressure fluctuations measured under the cloud are extremely high (Brennen et al., 1996, Kawanami et al., 1997). The flow mechanism causing these high pressure fluctuations is also unclear, and the current models are based on the assumption that they are caused by shock waves that develops within the bubble cloud (for example: Morch, 1980, 1981; Wang and Brennen, 1994; Noordzij & van Wijngaarden, 1974, Matsumoto, 1998). There is no experimental evidence for the existence of this shock, presumably due to the difficulties in measuring it.
The shedding process of large sections of the cavity has puzzled researchers for quite a while. If potential flow analysis is used there must be an unsteady reverse flow in the closure area and below the cavity. Thus, it has been argued that the shedding is caused by a “re-entrant jet”, a reverse flow that forms below the cavity and “pinches” it intermittently. (Kawanami et al., 1998; Avelan et al., 1988; Kubota et al., 1989, 1992; Larrarte et al., 1995; de Lange et al., 1994, Shen and Peterson, 1978; Furness and Hutton, 1975; Lush and Skip, 1986; Le et al., 1993; Callenaere et al., 1998 and many others). Velocity measurements performed by Kawanami et al. (1998) provided evidence of reverse flow with magnitude of the same order as the free stream velocity. They also showed that small fences installed on the wall, close to the point where the sheet cavitation ended, prevented the shedding of cloud cavitation. Callenaere et al. (1998) demonstrated the upstream motion of the contact point of the cavity with the wall prior to cloud shedding. However, they mention that when the cavity is thin there can be a situation where adverse pressure gradients are too weak for a re-entrant jet. This situation is consistent with the present observations, that at early stages of cavitation, there is no reverse flow below or downstream of the attached cavitation.
The present paper describes part of our ongoing effort to resolve the flow structure around and downstream of sheet cavitation. We use PIV to map the flow (mean and instantaneous), vorticity and turbulence as the cavitation index is reduced below the inception level. We provide evidence that the collapse of the cavities is a primary source of vorticity and that small changes in the size of the cavity cause substantial increase in the turbulence level and momentum thickness in the boundary layer downstream.
Experimental Setup and Instrumentation
Test Facility
To provide detailed answers on the flow structure it is convenient to perform the experiments in a setup that allows careful observations on the flow structure and bubble distributions. Some of the measurements must be performed at a very high magnification under controlled conditions that include boundary layer thickness and nature, local pressure gradients, surface roughness and properties, population of nuclei etc.. However, the facility must also allow operations at relevant Reynolds numbers (>106). These considerations have led to the design of the present experimental setup.
A schematic description of the test facility is provided in Figure 1 and the test section is described in more detail in Figure 2. The pumps are located 5 m below the test section reducing the likelihood of pump cavitation and the 1000 L tank is used for separating undesired free stream bubbles. The settling chamber contains screens and honeycombs to reduce the turbulence level (along with the 9:1 contraction) and the vertical tank above is used for controlling the pressure in the facility. The 6.35 cm ×5.08 cm test section has a minimum length of 41 cm and maximum entrance velocity of 13 m/s. Thus, it enables generation of boundary layers with Reynolds numbers (based on axial distance) well into the 106 range. Windows on all sides and a transparent contoured nozzle (which is actually part of the bottom window) enable unobstructed observations from all directions.
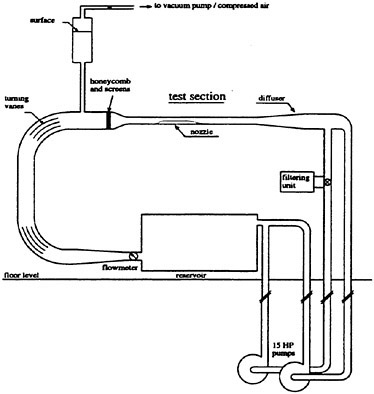
Figure 1: A Schematic description of the cavitation tunnel
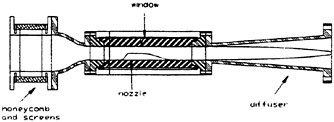
Figure 2: A close-up sketch of the test section.
The contoured surfaces in the test section were designed using a commercial CFD code (FLUENT). We chose pressure distributions that resemble a typical suction side of lifting surfaces at incidence. The typical pattern includes a region with low speed (stagnation), sharp decrease in pressure to a minimum, recovery to a pressure lower than the ambient pressure, a region of fairly constant low pressure and further increase to the ambient conditions. The computational grid was made sufficiently fine that further refinement did not affect the results and we used RNG for turbulence modeling. We assumed a free stream turbulence level of 1% (in reality it is significantly lower—about 0.1%) and a uniform inflow to the test section. Systematic evaluation of a series of designs eventually led to the geometries and pressure distributions shown in Figure 3 (they are all 5th order polynomials). They have different pressure gradients and minimum levels, but similar recovery at the trailing edge. Slots on the top and bottom walls of the tunnel, located upstream of the nozzle, can be used for boundary layer suction, using bypass lines and small pumps. Such capability is used for determining the effect of the boundary layer characteristics.
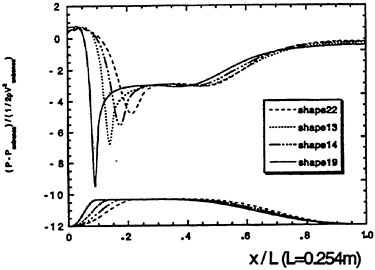
Figure 3: The selected nozzle geometries and the computed pressure distributions along their surfaces.
Measurement Techniques
Planar velocity measurements are performed using PIV. The data acquisition and analysis procedures have been developed in our laboratory for several years (Dong et al., 1992a, b; Chu et al., 1995a, b; Dong et al., 1997a, b; Sridhar and Katz, 1995, 1997; Liu et al., 1994). In the present experiments the light source is a dual head, 400 mJ/pulse, Nd-Yag laser whose beam is expanded to a 1 mm wide sheet. Images are recorded using a 2048 ×2048 pixels2, 4 frames/sec, digital camera manufactured by SMD. This camera has a custom, hardware based, image shifter that allows us to record two image on the same frame with a prescribed, fixed displacement between them (see Sinha and Katz, 1998 for details). This feature solves the directional ambiguity problem. We use in-house developed correlation based software for computing the velocity distributions. The vorticity is determined using 2nd order finite difference scheme. Calibrations and uncertainties are discussed in detail in Roth et al. (1995) and Sridhar and Katz (1995). In the PIV data of the cavitating flow, the size of an interrogation window is 1.35 mm and the distance between vectors is 0.68 mm, i.e. 50% overlap between windows.
As discussed in Sridhar and Katz (1995, 1998), by using fluorescent particles as velocity tracers we can easily distinguish between bubbles and particles within the illuminated plane. Bubbles reflect light and as a result maintain the original laser color (green—532 nm), whereas the particles fluoresce at 560–570 nm. During liquid velocity measurements, we use a filter that removes the green light, which
eliminates most of the bubble traces. When the bubble motion measured, we can use a filter that transmit only the laser wavelength (reflection from the microscopic particles is weak).
Results and Discussion
Cavitation Inception Indices and General Features:
The cavitation inception indices of sheet cavitation (σi) for three nozzles are shown in Figure 4. They are measured using visual observations by keeping the velocity constant and gradually reducing the pressure until cavitation appears. Each point is an average of many measurements that do not differ significantly. In all cases σi is lower than the computed −cpmin and there is little dependence on velocity. However, the difference between σi and −cpmin increases with increasing pressure gradients near the minimum pressure point. The difference can be as much as 10%. Thus, the model geometry clearly affects the inception indices beyond the magnitude of −cpmin. Consistent with previous results on sheet cavitation (Gindroz and Billet, 1994), the dissolved air content and free stream bubble distributions have insignificant effects on the inception indices. However, when the test facility contains high concentration of “large” bubbles (>1 mm) they destroy the “stable”, upstream portion of the attached sheet, as reported before in Katz (1984) and Ceccio and Brennen (1991).
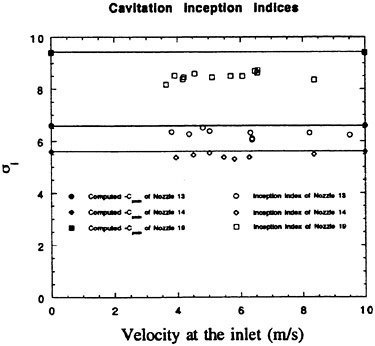
Figure 4: Cavitation inception indices for nozzles 13, 14 and 19 (shapes are shown in Figure 3).
Sample photographs of the cavitation in the nozzle are presented Zhang et al. (1998). It is shown there that at the leading edge the cavity surface is laminar, almost glossy. When the model surface is rough the glossy cavity at the leading edge is replaced by a series of thin “fingers” whose origins are fixed on small surface imperfections. Polishing of the very same surface transforms the leading edge to the blunt glossy shape. This stable region is followed by an area with distinct, orderly, two dimensional interfacial waves, identified before by Brennen (1970) as boundary layer instability waves. After a short distance the interface becomes increasingly unstable and rolls-up into a series of bubbly eddies that are being shed intermittently behind the attached sheet. The size and shedding frequency of these eddies on the same nozzle depend on the cavitation index. The process is consistent with the observations and modeling of Kubota et al. (1989, 1992) and many others mentioned in the introduction. Furthermore, even when si is only slightly below the inception level, the flow behind the attached cavitation consists of a series of either large scale bubble-containing eddies or thinner horse-shoe like vortices with vaporous cores. These eddies are considerably higher than any boundary layer structure that exists in the absence or upstream of the cavitation.
Flow Structure and Turbulence
All the data presented in this section has been obtained with nozzle No. 13. Two data series, both at the same velocity and pressure, but at different water temperatures, 35°C and 45°C, have been recorded. They provide essentially the same hydrodynamic conditions (the effect on viscosity is negligible), but the resulting cavitation indices, 4.69 and 4.41, respectively, vary slightly due to the different vapor pressure. As will be shown shortly, the impact on the cavitation and flow structure is substantial. We analyzed 30 vector maps at each condition. Due to the presence of bubbles along the walls, each image had to be examined carefully to remove the bubble traces before computing the velocity distributions. Otherwise the bubbles contaminate the liquid velocity measurements.
The velocity distribution prior to the onset of cavitation, created by combining several vector maps, is presented in Figure 5. For reference, the entrance velocity is 5.3 m/s. The result is consistent with the predictions until the point of boundary layer transition at x/L=0.58. Note that the transition occurs both at the upper and lower walls almost at the same cross section, but the thickness of the turbulent layer is significantly wider at the bottom, where the adverse pressure gradients are higher. Note that the average velocity near the bottom wall is still positive, i.e. there is no reverse flow that would characterize a separated regions. This phenomenon is consistent with transition in a region with adverse
pressure gradients and a boundary layer with an inflection point in the velocity distribution. Since the cavitation and flow phenomena of interest here occur upstream, at x/L<0.45, these transition phenomena are beyond the scope of the present paper.
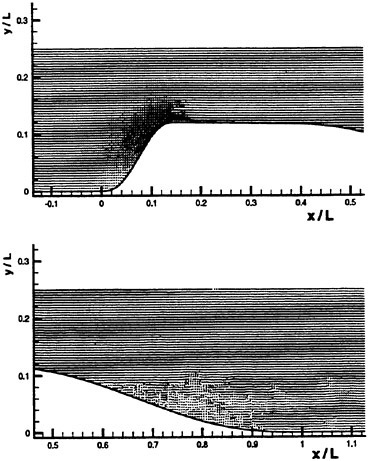
Figure 5: The measured velocity distribution in nozzle 13 prior to the onset of cavitation (L=0.254 m).
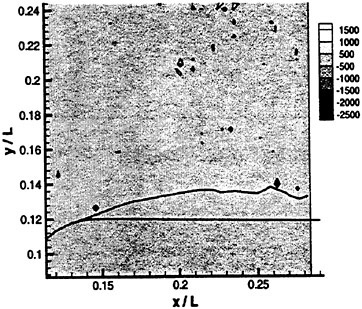
Figure 6: A sample Instantaneous vorticity distribution upstream and along the stable part of the attached cavitation (L=0.254 m).
A sample vorticity distribution of the flow upstream of the cavitation and along the stable glossy region of the interface is presented in Figure 6. Since the entire boundary layer upstream of the cavitation is very thin (<0.5 mm using simple laminar flow scaling) we cannot resolve the vorticity there. There are also no obvious signs of vorticity production along the stable parts of the cavitation interface. Conversely, as Figure 7 shows, as the interface becomes unstable and especially at the trailing edge of the cavitation, there is evidence of massive vorticity production. Although Figure 7 provides only two characteristic instantaneous samples, one for each cavitation index, the same phenomenon persists in all the data (additional samples are shown in Zhang et al. (1998).
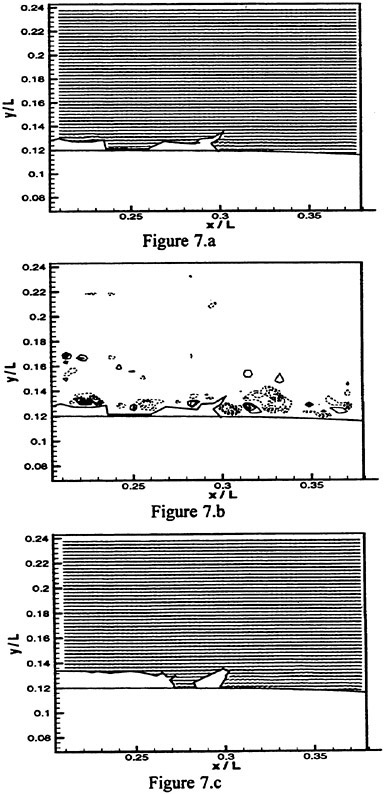
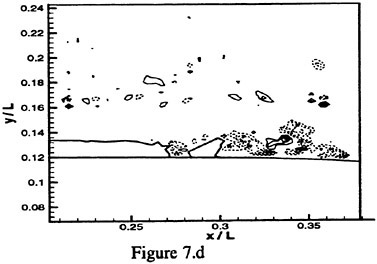
Figure 7: Sample instantaneous velocity maps, vorticity distributions and cavity shapes, a. velocity at σ=4.69; b. vorticity computed from the data in a; c. velocity at σ=4.41; d. vorticity computed from the data in c. For reference, the velocity at x/L=0.21, y/L=0.19 is 11 m/s (L=0.254 m). The incremental increase between lines in the vorticity distributions is 500 l/s. Solid lines—positive vorticity; dashed line—negative vorticity.
Several other trends can be readily observed from the instantaneous velocity distributions at the trailing edge of the cavitation. First, this region is characterized by patches of cavities at different stages of collapse (condensation). The length of the cavities varies from one image to the next and in some cases the odd-shaped patches are separated from the cavitation upstream. Second, the small difference in cavitation index, 4.61 vs. 4.41, increases the height and length of the cavitation significantly.
Third and most important, there is no reverse flow anywhere around the closure region of the cavitation. This conclusion is based not only on the samples shown here, but also on the entire data base available to us. We also checked individual traces of particles very near the wall in order to verify that there is no reverse flow at scales smaller than the size of the interrogation window. We have not seen even a single particle with negative horizontal velocity. Thus, at this level of cavitation there is no re-entrant flow, i.e. there is no shedding of cavities due to a reverse flow that penetrates under the cavitation. The “large” vapor cavities simply shrink as the vapor condenses and the horizontal velocity around them remains positive. This observation is not consistent with the typical re-entrant flow model for the closure region of attached cavitation (see the introduction). It agrees however with a comment made in a recent paper by Callenaere et al. (1998) that when the cavities are thin, the adverse pressure gradients may be too weak for creating a re-entrant jet. Note also that we do not claim here that there is no reverse flow under developed states of cloud cavitation. In fact, the observations during advanced cloud cavitation in the same facility suggest that intermittent reverse flow under the large bubbly eddies does exist (Zhang et al., 1998). However, in the present early stages of cavitation, there is no reverse flow in the closure region.
Returning back to the vorticity distributions, the closure region contains vorticity peaks of both signs but the negative peaks are dominant. Neither exists either upstream of the cavitation or along the stable part of the interface. Eventually, due to mixing, only negative peaks exist further downstream (data not shown here—see Zhang et al., 1998 for examples) and the boundary layer contains large eddies with negative circulation. Thus, vorticity production clearly occurs as the vapor cavities collapse.
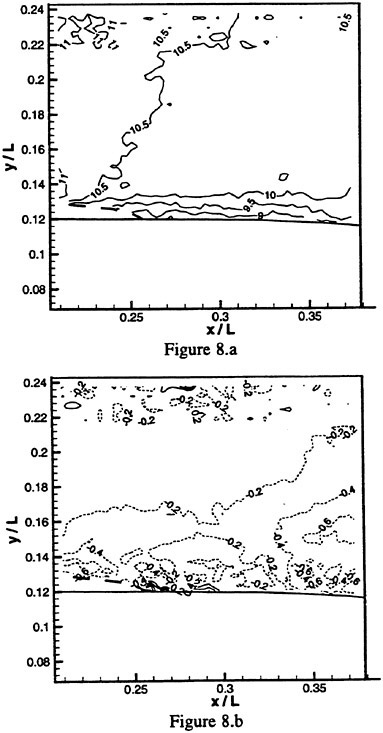
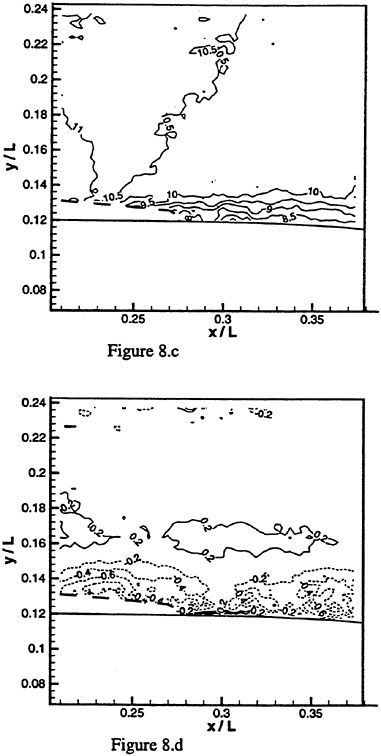
Figure 8: Average velocity distributions, a. ū at σ=4.69; b. ![]() at σ=4.69; c. ū at σ=4.41; d.
at σ=4.69; c. ū at σ=4.41; d. ![]() at σ=4.41. The incremental difference between lines for ū is 0.5 m/s and for
at σ=4.41. The incremental difference between lines for ū is 0.5 m/s and for ![]() is 0.2 m/s. The thick dashed line encloses the region that contains vapor in 20 of the 30 realizations.
is 0.2 m/s. The thick dashed line encloses the region that contains vapor in 20 of the 30 realizations.
Distributions of average horizontal and vertical velocities are presented in Figure 8a~d. The thick boundary downstream of the cavitating region is evident is both cases. We present data only for region where at least 10 out of the 30 instantaneous distributions contain liquid. The boundaries indicated in these plots identify these regions. The momentum thickness, θ, and the displacement thickness, δ*, for these cases are presented in Figure 9. They are determined from
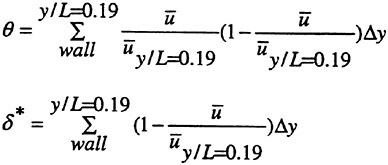
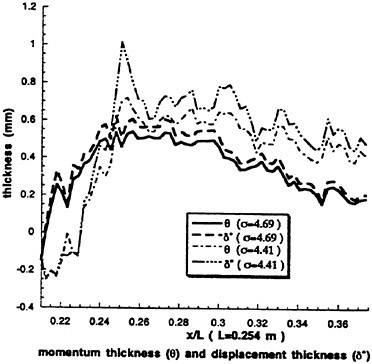
Figure 9: Momentum thickness and displacement thickness determined from the data in Figure 8.
It is evident that slight reduction in cavitation index causes substantial increase in the size of the vapor cavities as well as the displacement thickness and momentum thickness. Both δ* and θ remain constant for some distance and then start decreasing with increasing distance from the closure region. This trend is associated with the low (but still far from zero) velocity just behind the cavity. The streamwise increase in horizontal velocity (∂ū/∂x>0), is consistent also with the trends of the vertical velocity ![]() .
. ![]() around the cavity closure is negative except for a narrow region very close to the wall. As the flow converges, the horizontal velocity increases and the momentum thickness decreases. Note that at σ=4.41 the region with high constant θ starts further downstream (since
around the cavity closure is negative except for a narrow region very close to the wall. As the flow converges, the horizontal velocity increases and the momentum thickness decreases. Note that at σ=4.41 the region with high constant θ starts further downstream (since
the cavity is longer) and is longer than the corresponding region at σ=4.69. Also, at σ=4.41 θ decreases by about 25%, whereas at σ=4.69 it decreases by 50%. In both cases the momentum thickness starts decreasing at a point located close to the farthest extent of the cavitation.
Distributions of turbulence parameters for the two cases are presented in Figure 10. We recognize that an average of 30 instantaneous distributions is not sufficient for sound statistics, but this is the data available at the deadline for submitting this paper. We’ll continue expanding this data base. Consequently, Figure 11 demonstrates the effect of increasing the number of samples on the Reynolds stresses at an arbitrary point located within the turbulent flow downstream of the cavitation. It is evident that although the data is not completely converged the variations in the turbulence parameters become less and less significant with increasing number of samples. Thus, although the exact values may change with more data, the results in Figure 10 capture the essential trends.
Several phenomena are evident from the distributions of Reynolds stresses. In the area around the trailing edge of the cavitation and the region of high constant q immediately downstream (see Figure 9), the rms. values (u’ and v’) are particularly high and increase dramatically as s decreases slightly. At σ=4.69 the peak rms. values of both velocity components are about 13% of the local velocity in the middle of the test section or 26% of the velocity at the entrance to the test section. At σ=4.41 u’ reaches levels of 18% of the local velocity or 36% of the flow at the entrance to the test section, v’ is a little lower, only 15% and 30%, respectively. Note that these levels are significantly higher than velocity fluctuations in turbulent boundary layers (Hinze, 1975), but are comparable to peak levels within a separated region, for example, behind backward facing steps (Eaton and Johnson, 1980).
At σ=4.41 the highest normal stresses are measured at 0.30<x/L<0.32. This region is located just downstream of the farthest extent of the cavitation (the cavity covers this area only in one of the 30 samples) and typically contains high vorticity peaks. It also coincides with the point where the momentum thickness starts decreasing. At σ=4.69 the high normal stresses are located around 0.26<x/L<0.29, also at the end of the region with high momentum thickness. In this case patches of collapsing cavities cover part or all of this area in about a third of the instantaneous realizations. This region also contains high vorticity peaks. Thus, the collapse of vapor cavities and high vorticity production at the trailing edge of the attached cavitation also involves substantial increase in the turbulence levels. Note that the average quantities (including turbulence levels) for a certain point are computed using only the data for which this point is located in liquid.
The turbulent shear stresses, ![]() reach maximum levels at the same location as
reach maximum levels at the same location as ![]() and
and ![]() . Their peak values are 25%–40% of the normal stresses, i.e. significantly higher than that characteristic 15% in turbulent boundary layers (Hinze, 1975), but comparable to the characteristic 25% within a shear layer developing behind the backward facing step (Eaton and Johnson, 1980). Such high correlation between horizontal and vertical velocity fluctuations is characteristic to flows containing large coherent vortex structures, which is consistent with the presence of powerful eddies at the same location. However, unlike typical shear flows, in the closure region of attached cavitation the high vorticity is generated by collapse of the vapor cavities.
. Their peak values are 25%–40% of the normal stresses, i.e. significantly higher than that characteristic 15% in turbulent boundary layers (Hinze, 1975), but comparable to the characteristic 25% within a shear layer developing behind the backward facing step (Eaton and Johnson, 1980). Such high correlation between horizontal and vertical velocity fluctuations is characteristic to flows containing large coherent vortex structures, which is consistent with the presence of powerful eddies at the same location. However, unlike typical shear flows, in the closure region of attached cavitation the high vorticity is generated by collapse of the vapor cavities.
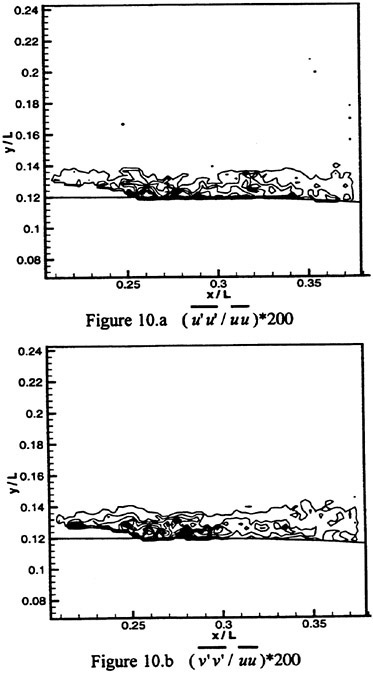
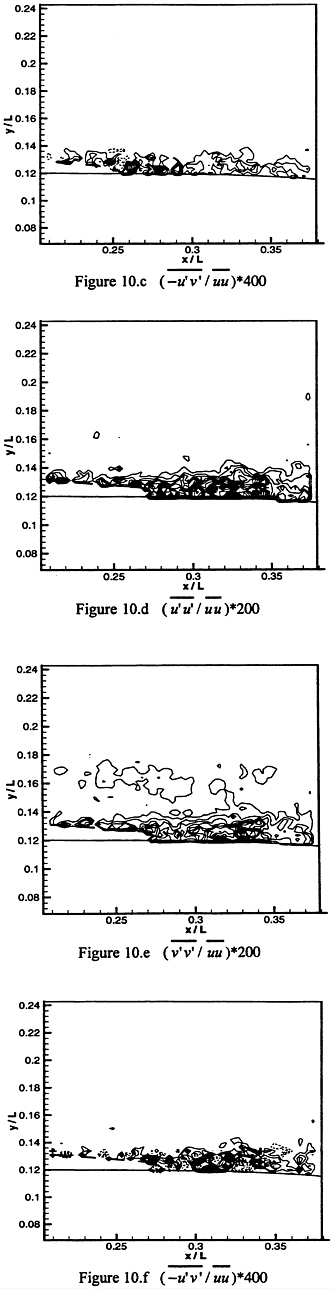
Figure 10: Distribution of ![]()
![]() respectively. Here
respectively. Here ![]() . In a, b and c σ=4.69; in d, e and f σ=4.41. Incremental increase between lines is 0.5. Note the different scaling factors.
. In a, b and c σ=4.69; in d, e and f σ=4.41. Incremental increase between lines is 0.5. Note the different scaling factors.
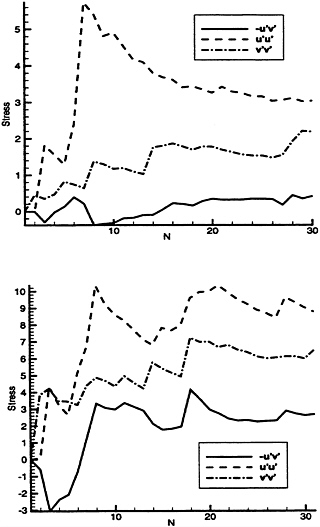
Figure 11: Demonstration of convergence of the turbulence data in an arbitrary point (x/L=0.34, y/L=0.13) located within the turbulent region downstream of the closure region, a. σ=4.69; b. σ=4.41. The dimension of stresses is m2/s2
Summary and Conclusions
PIV is used to resolve the flow structure at the closure region and downstream of attached cavitation. This paper focuses on the flow when the ambient pressure is reduced slightly below the cavitation inception level, i.e. when the cavity is thin (2–3 mm). Two sets of 30 vector maps recorded at the same hydrodynamic conditions but at slightly different water temperatures, 35°C and 45°C, provide data on the effect of small changes to the cavitation index (4.69 vs. 4.41) on the instantaneous and averaged flow structure, turbulence and vorticity production. Examinations of the instantaneous velocity distributions show that when the cavity is thin there is no reverse flow downstream and below the cavitation, i.e. there is no re-entrant flow. Instead, the cavities collapse as the vapor condenses. The shape of the cavities in the closure region is highly irregular and unsteady. The process cavity collapse involves substantial vorticity production.
The average velocity distributions demonstrate that the unsteady cavity collapse in the closure area involves substantial increases in turbulence, momentum and displacement thickness. A small decrease in cavitation indices increases the height and length of the cavity slightly, but has a major impact on the turbulence level and momentum deficit in the boundary layer downstream of the cavitation. The region with the highest turbulence level is located just downstream of the closure region. The Reynolds shear stresses reach levels of 25%–40% of the normal stresses. Such high correlations are characteristic to flows containing large coherent vortex structures that dominate this flow. However, unlike typical turbulent shear flow, the large eddies are originated as the vapor cavities collapse.
Acknowledgment
This project has been funded by ONR, under grant Numbers N00014–95–1–0329. The program manager is E.Rood. The authors would also like to thank Steven King for assembling the electronic control system and Manish Sinha that integrated the new digital camera.
References
1. Arakeri, V.H., Acosta, A.J., (1973), Viscous Effects in The Inception of Cavitation Axisymmetric Bodies, J. Fluids Eng., Vol. 95, pp. 519–527.
2. Arndt, R.E.A., Holl, J.W., Bohn, J.C., Bechtel, W.T., (1979), “The Influence Of Surface Irregularities On Cavitation Performance, J. Ship Research, Vol. 23, pp. 157–170.
3. Brennen, C., Reisman, G., Wang, Y.C., (1996), “Shock Waves in Cloud Cavitation” 21th Symposium on Naval Hydrodynamics, pp. 756–771.
4. Brennen, C., (1970), “Cavity Surface Waves Pattern and General Appearance,” J. Fluid Mechanics, Vol. 44, pp. 33–49.
5. Callenaere, M., Franc, J.P., Michel, J.M., (1998), “Influence of Cavity Thickness And Pressure Gradients On The Unsteady Behavior of Partial Cavities”, Third International Symposium on Cavitation, Grenoble, France, April, pp. 209–214.
6. Ceccio, S.L., Brennen, C.E., (1991), “Observations of The Dynamics And Acoustics of Traveling Bubble Cavitation”, J. Fluid Mechanics, Vol. 223, pp. 633–660.
7. Chu, S., Dong, S., Katz, J., (1995a), “Relationship Between Unsteady Flow, Pressure Fluctuations and Noise In A Centrifugal Pump. Parts A: Use of PDV Data to Compute The Pressure Field”, Journal of Fluids Engineering, Vol. 117, pp. 24–29.
8. Chu, S., Dong, S., Katz, J., (1995b), “Relationship Between Unsteady Flow, Pressure Fluctuations and Noise In A Centrifugal Pump. Parts B: Effects of Blade-Tongue Interactions”, Journal of Fluids Engineering, Vol. 117, pp. 30–35.
9. De Lange, D.F., de Bruin, G.J. & van Wijngaarden, L., (1994), “On the Mechanism of Cloud Cavitation-Experiments and Modeling-”, 2nd International Symposium on Cavitation (Cav. ’94), 45–50.
10. Dong, R., Chu, S., Katz, J., (1992a), “Quantitative Visualization of The Flow Structure Within The Volute of a Centrifugal Pump, Part A: Technique”, Journal of Fluids Engineering, Vol. 114, No. 3, pp. 390–395.
11. Dong, R., Chu, S., Katz, J., (1992b), “Quantitative Visualization of The Flow Structure Within The Volute of a Centrifugal Pump, Part B:
Results”, Journal of Fluids Engineering, Vol. 114, No. 3, pp. 396–403.
12. Dong, R.R., Katz, J., & Huang, T.T., (1997a), “On the Structure of Bow Waves on a Ship Model”, J. Fluid Mech., Vol. 346, 77–115.
13. Dong, R., Chu, S., Katz, J., (1997b), “Effect of Modification to Tongue And Impeller Geometry on Unsteady Flow, Pressure Fluctuations and Noise in A Centrifugal Pump”, ASME Journal of Turbomachinery, Vol. 119, pp. 506–515.
14. Eaton, J.K., Johnson, J.P., (1980), “Turbulent Flow Reattachment: An Experimental Study of The Flow And Structure Behind A Backward-Facing Step,” Report MD-39, Dept. of Mechanical Engineering, Stanford University, Stanford CA.
15. Furness, R.A. & Mutton, S.P., (1975), “Experimental and Theoretical Studies of Two-Dimensional Fixed-Type Cavities”, ASME Journal of Fluids Engineering, Vol. 97, No. 4, 515–522.
16. Gindroz, B., Billet, M.L., (1994), “Nuclei and Propeller Cavitation Inception”, ASME Symposium on Cavitation and Gas-Liquid Flow in Fluid Machinery and Devices, FED-Vol. 190, pp. 251–260.
17. Gates, E.M., Acosta, A.J., (1978), “Some Effects of Several Free Stream Factors on Cavitation Inception On Axisymmetric Bodies”, 12th Symp. Naval Hydrodynamics, Washington DC, pp. 86–108.
18. Harvey, E.M., McElroy, W.D., Whiteley, A.H., (1947), “On Cavity Formation in Water”, J. Appl. Phys., No. 18, pp. 162–172.
19. Hinze, J.O., (1975), “Turbulence—2nd Edition”, McGraw-Hill, New York
20. Katz, J., 1984, “Cavitation Phenomena within Regions of Flow Separation,” J. Fluid Mechanics, Vol. 140, pp. 497–536.
21. Kawanami, Y., Kato, H., Yamaguchi, H., Tanimura, M., Tagaya, Y., (1997), “Mechanism and Control of Cloud Cavitation”, J. Fluids Engineering, Vol. 119, pp. 788–794.
22. Kubota, A., Kato, H., Yamaguchi, H. & Maeda, M., (1989), “Unsteady Structure Measurement of Cloud Cavitation on a Foil Section Using Conditional Sampling Technique”, ASME Journal of Fluids Engineering, Vol. 111, No. 2, 204–210.
23. Kubota, A., Kato, H. & Yamaguchi, H., (1992), “A New Modeling of Cavitating Flows: a Numerical Study of Unsteady Cavitation on a Hydrofoil Section”, Journal of Fluid Mechanics, Vol. 240, 59–96.
24. Laberteaux, K.R., Ceccio, S.L., (1998), “Flow In The Closure Region Of closed Partial Attached Cavitation”, Third International Symposium on Cavitation, Grenoble, France, April, pp. 197–202.
25. Larrarte, F., Pauchet, A., Bousquet, Ph. & Fruman, D.H., (1995), “On the Morphology of Natural and Ventilated Cavities”, ASME Cavitation and Multiphase Flow, FED-210, 31–38.
26. Le, Q., Franc, J.P. & Michel, J.M., (1993), “Partial Cavities: Global Behavior and Mean Pressure Distribution”, ASME Journal of Fluids Engineering, Vol. 115, 243–248.
27. Liu, S., Meneveau, C., Katz, J., (1994), “On The Properties of Similarity Subgrid-Scale Models as Deduced From Measurements in A Turbulent Jet”, Journal of Fluid Mechanics, Vol. 275, pp. 83–119.
28. Lush, P.A. & Skipp, S.R., (1986), “High Speed Cine Observation of Cavitating Flow in a Duct”, International Journal of Heat Fluid Flow, Vol. 7, No. 4, 283–290.
29. Matsumoto, Y., (1998), “Bubble Dynamics in Cavitation”, Third International Symposium on Cavitation, Grenoble, France, April, pp. 3–8.
30. Morch, K.A., (1980), “On The Collapse of Cavity Cluster in Flow Cavitation” Proc. 1st international Conf. on cavitation and Inhomogeneities in underwater Acoustics, Springer Series in Electrophysics, No. 4, pp. 95–100.
31. Morch, K.A., (1981), “Cavity Cluster Dynamics and Cavitation Erosion”, ASME Cavitation and Polyphase Flow Forum, pp. 1–10.
32. Noordzij, L. & van Wijngaarden, L., (1974), “Relaxation Effects, Caused by Relative Motion, on Shock Waves in Gas-Bubble/Liquid Mixtures”, Journal of Fluid Mechanics, Vol. 66, 115–143.
33. Peterson, F.B., (1968), “Cavitation Originating at Liquid-Solid Interfaces”, DTNSRDC Rep. No. 2799.
34. Shen, Y.T. & Peterson, F.B., (1978), “Unsteady Cavitation on an Oscillating Hydrofoil”, 12th Symposium on Naval Hydrodynamics, 362–384.
35. Sridhar, G., Katz, J., (1995), “Lift and Drag Forces on Microscopic Bubbles Entrained by a
Vortex”, Physics of Fluids, Vol. 7, No. 2, pp. 389–399.
36. Sridhar, G., Katz, J., (1997), “Effect of Entrained Bubbles on The Structure of Vortex Rings”, submitted for Publication in the Journal of Fluid Mechanics.
37. Stutz, B., Reboud, J.L., (1997), “Experiments in Unsteady Cavitation”, Experiments in Fluids, Vol. 22, No. 3, pp. 191–199.
38. Tulin, M., (1953), “Steady Two Dimensional Flows About Slender Bodies”, DTMB Tech. Rep. 834.
39. Tulin, M.P., (1955), “Supercavitating Flow Past Foils and Struts”, Proc. NPL Symp. Cavitation Hydrodyn. paper no. 16, 1–19.
40. Tulin, M.P., (1964), “Supercavitating Flows—Small Perturbation Theory”, J. Ship Res. Vol. 7(3), 16–37.
41. Tulin, M., Hsu, C., (1980), “New applications of Cavity Flow Theory, Proc. 13th Symposium on Naval Hydrodynamics”, Tokyo.
42. Wang, Y.C., Brennen, C.E., (1994), “Shock Wave Development in The Collapse of A Cloud of Bubbles”, ASME Cavitation and Multiphase Flow Forum, pp. 15–19.
43. Wu, T.Y., (1962), “A Wake Model for Free-Stream Flow Theory. Part 1: Fully and Partially Developed Wake Flows and Cavity Flows Past an Oblique Flat Plate”, J. Fluid Mech., Vol. 13, 161–181.
44. Wu, T., (1972), “Cavity and Wake Flows”, Annual Review of Fluid Mechanics, Vol. 4.
45. Zhang, Y., Gopalan, S., Katz, J. (1998), “On The Flow Structure and Vorticity Production Due To Sheet Cavitation,” Proceedings of The ASME Fluids Engineering Summer Meeting, paper No. FEDSM98–5301, June 21–25, Washington DC.
DISCUSSION
R.Arndt
National Science Foundation, USA
Can you comment on the periodicity of the flow and how it changes with cavitation number?
AUTHORS’ REPLY
The flow is not periodic; i.e., the breakup process appears to be random, as long as the closure region of the cavitation is located on the straight part of the nozzle throat. In this region the horizontal pressure gradients in the closure region are small (x/L=0.2–0.4, see Figure 3 in the text). However, large scale periodic shedding starts as the cavitation index is decreased to a level that the closure region is located in the expanding part of the diffuser (x/L>0.5). In this region there are significantly higher adverse pressure gradients and there is clear reverse flow under the large cavities (re-entrant jet?). Thus, the occurrence of large scale shedding appears to be dependent on the pressure gradients in the closure region. We did not measure the shedding frequency.
Partial Attached Cavitation on Two- and Three-Dimensional Hydrofoils
K.Laberteaux, S.Ceccio (University of Michigan, USA)
ABSTRACT
Leading-edge attached cavitation on both two- and three-dimensional plano-convex hydrofoils was examined. Particle-streak photography, single-frame Particle Imaging Velocimetry (PIV), and cinemagraphic PIV were used to visualize the cavitating and non-cavitating flow. For moderately large attack angles, a region of flow separation exists near the hydrofoil’s leading edge. An attached cavity forms within the separation bubble when the cavitation number is reduced. For the two-dimensional hydrofoil, the partial cavities were open, the closure of the cavity was unsteady, and cavitating vortical structures were shed from the attached cavity. The cavity length and thickness were related to the non-cavitating separated flow. Re-entrant flow was not observed downstream of thin partial cavities. However, recirculating flow was observed downstream of cavities that formed within large regions of flow separation. The three-dimensional hydrofoils were plano-convex with varying degrees of sweep. The topologies of the cavities formed on the swept hydrofoils were substantially different from those of the cavities that formed on the two-dimensional hydrofoil under similar freestream conditions and attack angles. A portion of the cavity was vapor-filled, and the re-entrant flow was seen within the cavity. The introduction of three-dimensionality to the attached cavity resulted in the redirection of the re-entrant flow in the cavity closure. Large portions of these three-dimensional cavities were closed, and the flow in the closure region of the closed cavities was very steady. The profiles of the closed cavities were qualitatively similar to those predicted by two-dimensional free-streamline theory with a re-entrant flow closure.
1. INTRODUCTION
Hydrodynamic cavitation can cause pressure pulsations, noise, vibrations and erosion, which can seriously degrade the performance of hydromechanical systems. Attached (or sheet) cavitation is observed on lift producing surfaces and occurs when the flow detaches from a solid surface, forming a quasi-steady gas/vapor pocket. Bubbles can be entrained into the wake of the sheet cavity and collapse downstream of the cavity reattachment. Attached cavitation can be further classified as either closed or open depending on the flow in the closure region of the cavity. A closed partial cavity has a relatively stable cavity length, while an open cavity has a periodically varying length which is associated with the shedding of vapor-filled vortices. Under some conditions, large portions of the sheet cavity can periodically break off to form large bubbly clouds (i.e. cloud cavitation).
The inception and dynamics of attached cavitation is of considerable interest to designers of ship propellers. Ideally, designers of these devices would have analytical tools which could be used to predict the occurrence of sheet cavitation, and its potential for instability and erosion. Today, however, the current design tools can only predict the general location of sheet cavitation inception, and this is usually done by examining the fully wetted potential flow around blade surfaces of the propeller.
Researchers have experimentally examined the physical mechanisms responsible for the formation of attached cavitation (e.g. Arakeri [1], Franc and Michel [6], Tassin-Leger and Ceccio [24], and Tassin-Leger et al. [25]). Detailed measurements of the flow near attached cavities are made difficult by the large range of scales in the flow, the presence of two phases, and the unsteadiness of the cavity surface and closure region. The formation of cloud cavitation downstream of partial cavities is attributed to the re-entrant flow in the cavity closure and is discussed by Knapp et al. [12] and Furness and Hutton [7], among others.
Recent experimental investigations of attached cavitation include Lush and Skipp [19], Avellan et al.
[2], Kubota et al. [13], Maeda et al. [20], Larrarte et al. [16], Le et al. [17, 18], Reisman and Brennen [22], Kawanami et al. [10, 11], and de Lange [5]. The details of the flow surrounding both steady and unsteady attached cavitation have been examined using a variety of experimental techniques. Avellan et al. [2] and Kubota et al. [13] employed Laser Doppler Velocimetry (LDV) to determine the mean and phase averaged flow field around partial cavities which formed on two-dimensional hydrofoils. Le et al. [17, 18], Reismann and Brennen [22], and Larrarte et al. [16] employed mean and dynamic pressure measurements in the vicinity of cavities which formed on a two-dimensional hydrofoil. Kawanami et al. [10] examined the effect of surface barriers on the re-entrant flow within the cavity using surface pressure sensors in conjunction with cinemagraphic observations.
Avellan et al. [2] and Kubota et al. [13] examined the production of cavitating vortical structures in the closure region of open partial attached cavitation. Maeda et al. [20] used holography and Pereira [21] used stereography to examine the cavitating vortical structures which form at the closure of a closed cavity on a two-dimensional hydrofoil. Kawanami et al. [11] has recently examined the three-dimensional characteristics of the cavitating vortices which are shed downstream of cavities that formed on two-dimensional hydrofoils. Laberteaux et al. [14] examined the collapse of these vortical structures.
Most of the above studies examined cavitation that formed on two-dimensional and axisymmetric test objects. Fewer fundamental studies have been performed on three-dimensional test objects. Crima [4] and Ihara [9] examined attached cavitation which formed on hydrofoils with significant sweep. Bark [3] and Hart et al. [8] examined cavitation on oscillating rectangular planform hydrofoils with one fixed end. More recently, de Lange [5] examined both open and closed cavities that formed on two- and three-dimensional hydrofoils.
A general understanding of attached sheet cavitation has emerged from these and other studies.
-
Partial cavities can be filled with vapor or a high void-fraction bubbly mixture.
-
Cloud cavitation can intermittently or periodically be shed from open partial cavities. The frequency of large cloud formation, f, scales with the freestream velocity, U, the cavitation number, σ, and the cavity length, LC, to give a relatively constant Strouhal number:
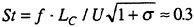
-
Re-entrant flow can occur in the cavity closure. The existence, momentum, and direction of the re-entrant flow will profoundly effect the cavity flow and the formation of cloud cavitation. The re-entrant flow can cause periodic filling and break off of the cavity, leading to the formation of cloud cavitation. The impingement of the re-entrant flow on the cavity interface leads to the shedding of vapor-filled vortices.
-
The appearance and dynamics of three-dimensional partial cavities can be substantially different from those of two-dimensional cavities.
In the present study, we use advanced flow visualization techniques to examine the physical mechanisms associated with closed and open attached cavitation on hydrofoils. Both particle streak photography and Particle Image Velocimetry (PIV) are employed. Two- and three-dimensional hydrofoils are used to study the cavitating and non-cavitating flows. The fully wetted flow is examined using particle streak photography to understand the separation characteristics of the geometry. Particle Image Velocimetry is used to characterize the average and unsteady flow associated with the attached cavities. The physical characteristics of the cavity (i.e. size, shape) were related to the fully wetted separated flow and the flow in the cavity wake.
2. EXPERIMENTAL METHODS
The experiments described here were conducted in the Cavitation and Multiphase Flow Laboratory at the University of Michigan, Department of Mechanical Engineering and Applied Mechanics. Measurements were made in the Blow Down Water Tunnel (BDWT), and a description of this facility is provided in Tassin el al. [23]. The BDWT consists of two 1.5 m3 tanks connected through a square contraction (area ratio 4.4:1), a test section, and a diffuser. The test section has a 76.2 mm square cross section and a length of 260 mm. Controlled application of pressure and vacuum to the two tanks is employed to produce the desired flow in the test section. Between 10 and 20 seconds of steady flow can be produced with velocities in the range of 5 to 20 m/s. The test section velocity is determined by measuring the pressure difference between the test section entrance and the contraction entrance. This pressure difference was related to the test section velocity using LDV measurements of the
Figure 1: (a) Two-dimensional plano-convex hydrofoil. (b) Three-dimensional plano-convex hydrofoil, where the sweep angle, β, is equal to 30°, 15°, or 5°.
average flow velocity in the center of the empty test section. The free and dissolved air content of the BDWT can be qualitatively controlled through deaeration and by allowing free gas bubbles to reach the free surfaces in the two tanks.
Both two and three-dimensional plano-convex hydrofoils were employed during these experiments to produce partial cavities. Figure 1 shows the schematics of the hydrofoils. The plano-convex geometry was chosen to achieve separation at the leading edge of the foil. All hydrofoils are made of brass, and have a chord length of 127 mm and a width of 78 mm. The two-dimensional foil has a sweep angle, β, of 0°, whereas the three-dimensional foils have a sweep angle of either 30°, 15°, or 5°. The maximum thickness of the hydrofoils is 12.7 mm. The angle of incidence, α, varied from 1° to 5°. The Reynolds number based on the hydrofoil chord length varied from 9.0×105 to 1.1×106.
Particle streak photography is used to visualize the streamlines in the fully wetted flow and the corresponding separation bubble on each hydrofoil. The flow is seeded with fluorescent latex particles with an average diameter of 30 μm. An Nd-YAG laser is used to illuminate the flow with a continuous wave light sheet. A 35 mm Nikon camera is equipped with a filter to block the scattered laser light while recording the fluorescent return of the particles. A shutter speed of 1/250 second is used to capture the path of the particles as they traveled through the field of view. The particle streak images are digitized, and the visualized separation bubble is measured.
Double-pulsed, single-frame particle image velocimetry (PIV) is used to investigate the flow field in the closure region of the cavity. The details of the single-frame PIV experimental setup are provided in Tassin et al. [23] and Yu [27]. The instantaneous velocity profiles of a given flow are determined by analyzing the motion of the tracer particles on the recorded images. The flow is seeded with fluorescent latex particles with an average diameter of 30 μm. Seeding of the flow with particles does not result in the addition of active cavitation nuclei. By employing fluorescent particles, it is possible to distinguish Lagrangian flow tracers from the small bubbles present downstream of the cavity closure. Two frequency-doubled Quanta Ray Nd-YAG GCR130 lasers are used to produce a pulsed light sheet. A 35 mm Nikon camera is again equipped with a filter to block the scattered laser light while recording the fluorescent return of the particles. An oscillating mirror system from General Scanning Inc. is used to impose an image shift, eliminating directional ambiguity inherent in single-frame, double-pulsed images.
A double-pulsed, cinemagraphic Particle Image Velocimetry (PIV) system has been developed that is capable of capturing a series of consecutive double-pulsed images at a high repetition rate (>10,000 frames/second). This system consists of two fast-flashing Nd-YAG lasers (30 kHz maximum repetition rate), a Photec 16 mm high speed rotating prism camera (10 kHz maximum framing rate), and associated timing and synchronization electronics. The system is triggered by the BDWT monitoring and control system when the desired flow is achieved. The time series data is used to reveal the unsteady processes associated with attached cavitation near the closure region.
The double-pulsed images recorded on the photographs are digitized and processed to determine particle pairs. The thickness of the light sheet was sufficient to prevent tracer particles from leaving the sheet between the two pulses of the laser. The vector field is reconstructed from the filtered images using the software packages VISIFLOW© by AEA Technology and INSIGHT© by TSI Inc. PIV images are analyzed using autocorrelation. Velocity vectors are determined close to the solid surfaces and the gas/liquid interfaces of the bubbles. The image shift for the single-frame images is introduced during post-processing of the images.
3. TWO-DIMENSIONAL HYDROFOIL
3.1 Non-Cavitating Flow
The non-cavitating flow near the leading edge of the two-dimensional hydrofoil was examined using particle streak photography and single-frame PIV. Figure 2 shows images obtained with streak photography. At low attack angles (α<2°), the flow separation was detected near the hydrofoil leading edge. As the attack angle is increased, the length and thickness of the separation bubble increases. Figure 3 presents a plot of the separation bubble thickness, hS, versus the bubble length, LS, for a range of hydrofoil attack angles. The ratio of bubble thickness to length is approximately constant with hS/LS=0.13±0.03. Data for the case of α=2° was particularly difficult to gather since the thickness of the cavity is on the same order as the thickness of the boundary layer downstream of the cavity.

Figure 2: Streak photography of the flow near the leading edge on the suction side of the two-dimensional hydrofoil. As the attack angle increases, the flow separates near the foil leading edge. Four cases are shown: (a) α=5°, U=8.0 m/s, σ=4.1; (b) α=4°, U=8.0 m/s, σ=3.5; (c) α=3°, U=8.1 m/s, σ=2.7; (d) α=2°, U=8.0 m/y, σ=2.5.
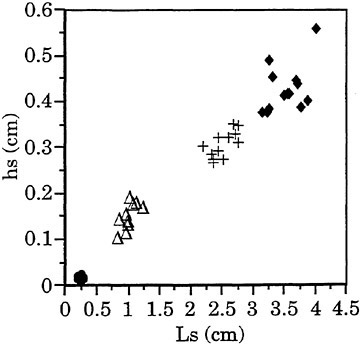
Figure 3: Plot of the separation bubble thickness, hS, versus separation bubble length, LS, for varying attack angles. (●) α=2°, (Δ) α=3°, (+) α=4°, (◆) α=5°.
3.2 Cavitating Flow
3.2.1 Cavity Appearance
As the static pressure was lowered, attached cavitation forms on the suction side of the hydrofoil near the leading edge. The process of cavity inception differed for cases of low and high attack angles. For low attack angles (α<3°), the cavity first appears when vapor fills the small region of flow separation. With decreasing static pressure (cavitation number), the original region of flow separation becomes completely filled with vapor, and the cavity begins to grow beyond the extent of the original separated region. These developed cavities are vapor-filled near the point of cavity detachment, but are filled with a liquid/vapor mixture for most of the cavity length. Vapor-filled vortices are shed downstream of the cavity. Figure 4 shows three images of cavities forming on the hydrofoil for α=2°. For higher attack angles (α>3°), inception of cavitation occurs within the vortices of the shear layer that exists at the boundary of the separation bubble. Both spanwise and streamwise vortices are visualized as vapor fills their cores. As the pressure is decreased, the separation bubble fills with a liquid/vapor mixture. Near the point of cavity detachment, the cavity is vapor-filled. Figure 5 shows three images of cavities forming on the hydrofoil for α=5°. The cavitating shear layer is easily seen in Figure 5a.

Figure 4: Cavitation on the two-dimensional hydrofoil at α=2°. (a) U=9.2 m/s, σ=0.8 (b) U=9.5 m/s, σ=0.63 (c) U=9.4 m/s, σ=0.6.
3.2.2 Cavity Geometry
Figures 6 and 7 show streak photography images of the cavitation as it forms on the two-dimensional hydrofoils for attack angles of 2° and 5°, respectively. For low attack angles, the cavity fills the separation bubble and grows beyond the separated region. At higher angles of attack, the cavities do not grow beyond the separated region of the fully wetted flow. The cavity thickness, hC, is plotted against cavity length, LC, in Figure 8. Cavities forming at higher attack angles are shorter than the length of the original separation bubble. Also plotted on the figure is the sum of the cavity length and the length of the flow reattachment downstream of the cavity for α=5°. These data show that the dimensions of the cavitating separated bubble are qualitatively similar to those of the non-cavitating separated flow.

Figure 5: Cavitation on the two-dimensional hydrofoil at α=5°. (a) U=9.1 m/s, σ=2.2 (b) U=9.6 m/s, σ=1.7 (c) U=9.6 m/s, σ=1.5.
The two-dimensional cavity can be compared to the profile predicted with free-streamline theory. As reported by Laberteaux and Ceccio [15], the profiles of the experimentally observed and predicted cavities coincide up to the point of maximum cavity thickness. Downstream of the point of maximum thickness, the experimentally observed cavity breaks up, and the flow in the closure region is very unsteady. This differs from the cavity closure predicted with free-streamline theory, where a re-entrant jet closure condition is used. In this case, the cavity smoothly curves back toward the solid surface to form a thin liquid jet.

Figure 6: Streak photography images of cavitation forming at the leading edge of the two-dimensional hydrofoil at α=2°. (a) U=9.2 m/s, σ=1.4 (b) U=9.5 m/s, σ=1.2 (c) U=9.5 m/s, σ=1.0.
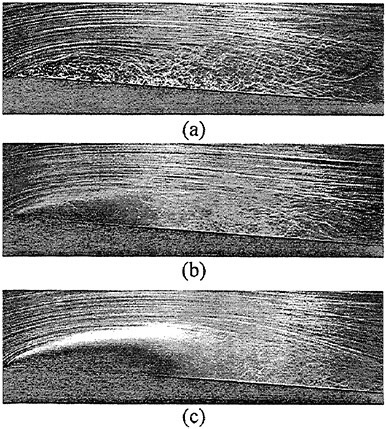
Figure 7: Streak visualization images of cavitation forming at the leading edge of the two-dimensional hydrofoil at α=2°. (a) U=8.6 m/s, σ=3.5 (b) U=9.5 m/s, σ=2.3 (c) U=9.6 m/s, σ=1.9.
3.2.3 Flow Visualization in the Cavity Closure
Figure 9 presents PIV velocity vector plots for attack angles of 2° and 5°. For the low attack angle condition, the cavity is thin and the flow in the closure does not recirculate. Analysis of many images did not
Figure 8: Plot of the cavity thickness, hC, versus cavity length, LC, for varying attack angles, (○) α=2°, (Δ) α=3°, (+) α=4°, (◊) α=5°. Also plotted is the cavity thickness versus the sum of the cavity length and reattachment length at α=5° (Θ). The solid lines represent the data for the non-cavitating separation bubble, hS</LS=0.13±0.03.
reveal flow in the upstream direction. However, recirculation can be seen for the high attack angle cases. At higher attack angles, the cavity does not fill the original non-cavitating separation bubble.
The flow in the cavity closure is very unsteady and three-dimensional, even for a cavity of nominally constant length. Vapor from the cavity is rolled up into vortical flow structures which are convected downstream. Figure 10 shows a time series of the flow field near a closed partial attached cavity on the two dimensional plano-convex hydrofoil at α=2° and 5°. This time series was acquired at a rate of 2000 frames
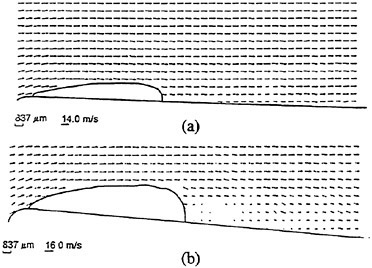
Figure 9: PIV instantaneous velocity vector fields on two dimensional foil, (a) α=2°, U=9.3 m/s, σ=0.77 (b) α=5°, U∞=9.2 m/s, σ=1.91.

Figure 10: Cinemagraphic PIV images in the closure region of cavities on the two-dimensional hydrofoil (β=0°). (a) α=2°, U=9.5 m/s, σ=0.8, (b) α=5°, U=9.3 m/s, σ=1.9. The series progresses from top to bottom, left to right. The flow is from left to right. The time interval between each frame is 500 μs.
per second. The evolution of individual vortical structures can be seen, and the variation of cavity length with time reveals the unsteadiness of the flow. The shedding of the small cavitating vortices is quasi-periodic, with a shedding frequency of approximately 300 to 400 Hz. The Strouhal number of cavity shedding is then ![]() . This is consistent with the Strouhal numbers for cloud shedding measured by Kawanami et al. [11].
. This is consistent with the Strouhal numbers for cloud shedding measured by Kawanami et al. [11].
4. THREE-DIMENSIONAL HYDROFOILS
Previous researchers have demonstrated that attached cavitation on swept hydrofoils can differ substantially from cavitation that occurs on two-dimensional hydrofoils of the same cross-sectional profile. In this study, three-dimensional effects were examined with the introduction of sweep to the two-dimensional plano-convex hydrofoil. Three swept hydrofoils were examined with sweep angles, β, of 30°, 15°, and 5° (Figure 1).
4.1 Non-Cavitating Flow
The non-cavitating flows on the swept hydrofoils were examined with particle streak photography. Streak images were recorded at three different spanwise locations on the hydrofoils. Planes parallel to the mean flow direction were examined at locations which were 30%, 50%, and 70% of the line spanning the test section. The location of the planes is shown in Figure 11, and these planes will be referred to as the left, mid, and right planes, respectively.
Figure 11: Location of the three planes used for streak photography. The planes are at 30% (left), 50% (mid), and 70% (right) of the line spanning the test section.
The leading edge separated region on the three-dimensional foils differ from the corresponding separated region on the two-dimensional hydrofoil. The non-cavitating flow on the suction side of the 30° sweep angle hydrofoil is shown in Figures 12 and 13. The attack angles are 2° and 5°, respectively. The separation bubble grows thicker and longer for planes farther away from the upstream vertex of the hydrofoil, towards the right plane (70%). On the left plane (30%), the streamlines near the boundary of the separation bubble reattach smoothly compared with the two-dimensional separation bubble.
Previous experimental observations of high sweep-angle “delta” wings suggest that an attached leading edge vortex has formed on the swept hydrofoil (see, for example, Thwaites [26]). In this case, there is flow within the separation bubble with a strong component parallel to the direction of the swept leading-edge, and the re-entrant flow at the closure of the separation bubble may be entrained into the vortex. Such a process will result in a much smoother flow reattachment compared with the two-dimensional separation bubble. The leading edge vortex will be
Figure 12: Streak photography on the suction side of the non-cavitating flow near the leading edge of a swept hydrofoil. The sweep angle, β, is 30°, and α=2°. (a) right plane, U=9.5 m/s, σ=2.7 (b) mid plane, U=9.5 m/s, σ=2.7 (c) left plane, U=9.6 m/s, σ=2.5.

Figure 13: Streak photography on the suction side of the non-cavitating flow near the leading edge of a swept hydrofoil. The sweep angle, β, is 30°, and α=5°. (a) right plane, U=9.0 m/s, σ=4.5 (b) mid plane, U=9.1 m/s, σ=4.2 (c) left plane, U=9.1 m/s, σ=4.2.
disturbed at spanwise locations near the right plane due to the presence of the test section wall. This is evident from the turbulent reattachment of the separation bubble visualized at the right plane.
Figure 14 presents a plot of the separation bubble thickness versus the bubble length for α=2° and 5° for the three spanwise planes. The range hS/LS=0.13±0.03 determined for the two-dimensional leading edge separation bubble is also shown. Most of the data fall within this range. At α=2°, the separation bubble on the swept hydrofoil is consistently thicker and longer compared to the two-dimensional separation bubble. For α=5°, the separation bubble on the swept hydrofoil at the left plane is much shorter than the equivalent condition on the two-dimensional hydrofoil. hS/LS≈0.19 for this case. Otherwise, the separation bubbles on the mid and right planes fall within the range of the two-dimensional data.
Figure 14: Plot of the separation bubble thickness, hS, versus separation bubble length, LS, at left, mid and right planes of three-dimensional hydrofoil, β=30°. α=2°, (○) left plane, (●) mid plane, (+) right plane. α=5°, (◊) left plane, (◆) mid plane, (Δ) right plane. The solid lines represent the data for the non-cavitating separation bubble on the two-dimensional hydrofoil, hS/LS=0.13±0.03.
4.2 Cavitating Flow
4.2.1 Cavity Appearance
The freestream pressure was reduced, and cavitation was observed on the suction side of the swept hydrofoils. Images of the cavitation are shown in Figures 15 and 16 for sweep angles of 30°, and attack angles of 2° and 5°, respectively. The images shown correspond to three different cavitation numbers. Inception takes place at the upstream vertex of the hydrofoil in the region of flow separation, as seen in Figures 15a and 16a. A small portion of the separation bubble fills with vapor, while the remaining portion of the separated region exhibits shear layer cavitation. As the cavitation number is reduced, the spanwise extent of the vapor-filled region increases.
Re-entrant flow can be seen through the smooth cavity interface. The direction of the flow is approximately perpendicular to the freestream direction, de Lange [5] discusses how the re-entrant flow is “reflected” at the closure of three-dimensional partial cavities, and these observations are consistent with this process. A layer of re-entrant liquid flows within the cavity until it impinges on the cavity interface, as seen in Figures

Figure 15: Cavitation on the three-dimensional hydrofoil with β=30°, α=2°. (a) U=9.8 m/s, σ=1.0 (b) U=9.9 m/s, σ=.72 (c) U=10.1 m/s, σ=0.7.
15b, 15c, 16b, and 16c. A vapor/liquid mixture results that is similar to that observed on the two-dimensional hydrofoil. In some cases, the vapor-filled cavity may reform after the re-entrant flow has impinged, as seen in Figures 15b and 16b. The closure of the vapor-filled cavity is steady, and no bubbles or cavitating vortices are shed downstream. These portions of the cavity are closed. Once the re-entrant liquid impinges on the cavity interface, bubbly clouds are shed from the now open cavity. Figure 17 presents a comparison of the partial cavitation that forms on the two- and the three-dimensional hydrofoils for nominally the same test conditions. Introduction of sweep substantially changes the topology of the two-dimensional cavity.
Figure 16: Cavitation on the three-dimensional hydrofoil with β=30°, α=5°. (a) U=9.0 m/s, σ=2.4 (b) U=9.6 m/s, σ=1.9 (c) U=9.6 m/s, σ=1.5.

Figure 17: (a) Two-dimensional foil, β=0°, α=2°, U=9.4 m/s, σ=0.6. (b) Three-dimensional foil, β=30°, α=2°, U=10.1 m/s, σ=0.7.

Figure 18: Streaks for 3 planes β=30°, α=2°. left plane: (a) U=9.1 m/s, σ=1.3 (b) U=9.5 m/s, σ=1.1. (c) U =9.6 m/s, σ=0.9. mid plane: (a) U=9.2 m/s, σ=1.3. (b) U=9.5 m/s, σ=1.1. (c) U=9.8 m/s, σ=0.9. right plane: (a) U=9.2 m/s, σ=1.3. (b) U=9.6 m/s, σ=1.0. (c) U=9.8 m/s, σ=0.9.

Figure 19: Streaks for 3 planes β=30°, α=5°. left plane: (a) U=9.0 m/s, σ=4.5. (b) U=8.9 m/s, σ=2.7. (c) U =9.6 m/s, σ=1.7. mid plane: (a) U=8.7 m/s, σ=2.85. (b) U=9.6 m/s, σ=1.7. (c) U=9.7 m/s, σ=1.5. right plane: (a) U=8.9 m/s, σ=2.5. (b) U=9.5 m/s, σ=1.9. (c) U=9.6 m/s, σ=1.5.
Figures 18 and 19 show a series of streak images at the three spanwise planes for three different cavitation numbers and attack angles of 2° and 5°, respectively. Case (a) is the non-cavitating flow, case (b) is for inception, and case (c) is for developed cavitation. Inception starts at the upstream vertex of the hydrofoil within the region of flow separation. Initially, the cavitation does not modify the shape of the separation bubble. As the cavitation number is decreased, the closed portion of the cavity (left plane) grows beyond the length of the separation bubble. The cavity at the mid plane can be either open or closed, depending on the specific condition. The cavity at the right plane was almost always open, but it was possible at low attack angles to have a closed cavity that nearly spans the test section.
4.2.2 Cavity Geometry
The cavities that form on the swept hydrofoil differed from those on the two-dimensional hydrofoil. At α=5°, the cavities on the two-dimensional hydrofoil did not fill the original non-cavitating separated region. These cavities did not significantly modify the length and thickness of the original separation bubble. For similar conditions on the swept hydrofoil, the developed closed cavity always grows beyond the original noncavitating separation bubble. This is seen in Figure 20, which is a plot of the cavity thickness versus cavity length for attack angles of 2° and 5° compared with the data from Figure 14. The length of the closed cavity is approximately 1.5–2 times the length of the original non-cavitating separation bubble. It was difficult to measure the cavity geometry for the open portions of the cavities due to the large quantity of shed bubbles and cavitating vortices.
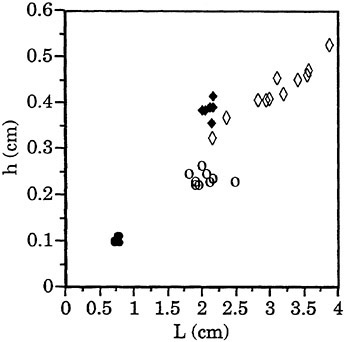
Figure 20: Plot of the cavity thickness, hC, versus cavity length, LC, for α=2° (○) and α=5° (◊), β=30°. Data taken on left plane of three-dimensional hydrofoil for the closed portion of the cavity. Also shown is the data of the non-cavitating separation bubble thickness, hS, versus separation bubble length, LS, for α=2° (●) and α=5° (◆).
4.2.3 Flow Visualization in the Cavity Closure
The flow in the closure region of the closed portion of a cavity was examined with PIV. Figure 21 shows a double-pulsed PIV image and the corresponding velocity vector plot for such a closed cavity on the left plane. The flow in the cavity closure is streamlined. Unlike the two-dimensional cavity wake, it is difficult to visualize the thin, wall-bounded shear flow
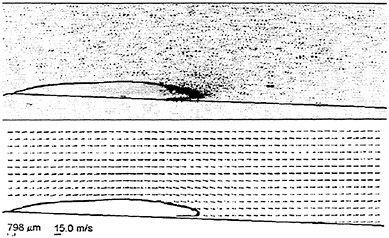
Figure 21: PIV image of the closed cavity on the left plane of the three-dimensional hydrofoil. β=30°, α=2°. U=9.4 m/s, σ=0.8.
downstream of the cavity closure. The thin layer of re-entrant fluid can be seen.
Cinemagraphic PIV imaging of the closed cavity reveals that the cavity geometry is steady. Figure 22 shows a series of images acquired at 2000 frames/second. The cavity flow is nearly identical in each frame. This is in contrast to the very unsteady closure of the two-dimensional cavity illustrated in Figure 10.
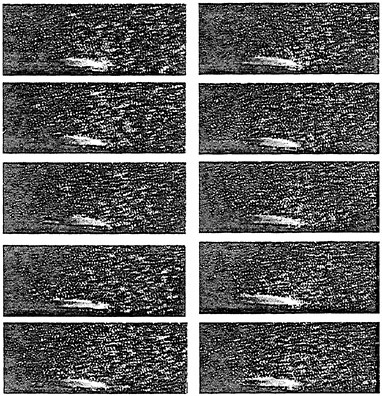
Figure 22: Cinemagraphic PIV images of cavity closure on left plane of three-dimensional hydrofoil, β=30°, α=2°. U=9.8 m/s, σ=0.75. The time series progresses from top to bottom and left to right. The flow is from left to right. The time interval between images is 500 μs.
Figure 23: Cavity profiles for cavities on (a) the two-dimensional hydrofoil (b) the swept hydrofoil, β=30°. α=2°, and the cavities were matched with the maximum thickness. The freestream conditions were: (a) U=9.3 m/s, σ=0.8, (b) U=9.4 m/s, σ=0.8. The closed cavity occurred on the left plane, (c) presents experimental cavity profiles for cavitation that occurred at the vertex of a wedge (symbols) and the accompanying analytical solution from free-streamline theory (solid line). The experimental conditions were wedge angle=20.5°, σexperiment=1.9, 2.1 and σanalytical=2.1, 2.4 (Laberteaux and Ceccio [15]).
The cavity profiles of the open and closed cavities are compared in Figure 23 (a) and (b). Figure 23 (a)

Figure 25: Effect of sweep angle at α=5°. β=15°, (a) U=9.2 m/s, σ=2.3 (b) U=9.9 m/s, σ=1.6. β=5°, (a) U=9.1 m/s, σ=2.0 (b) U=9.6 m/s, σ=1.6.
shows the profile of a cavity that was observed on the two-dimensional hydrofoil, and Figure 23 (b) shows a closed cavity that was observed on the swept hydrofoil. The cavity thickness and hydrofoil attack angles were matched, and the freestream conditions were approximately matched. The cavity on the three-dimensional foil is longer than the cavity on the two-dimensional foil, and the closed cavity smoothly closes back to the hydrofoil surface.
The profile of the closed, stable cavity is qualitatively similar to the two-dimensional profile predicted with free-streamline theory. Figure 22 (c) presents results reported by Laberteaux and Ceccio [15] for cavities that formed on the vertex of a wedge. Free-streamline theory was used with a re-entrant closure model to predict the cavity profile. The experimentally observed cavity profile for the cavity on the wedge is similar to the cavity profiles recorded for the two-dimensional hydrofoil. These are open cavities that are truncated near the point of maximum thickness. The theoretically predicted cavity for the wedge is qualitatively similar to the closed cavity which formed on the swept hydrofoil.
4.2.4 Effect of Hydrofoil Sweep Angle
The cavitating flow on hydrofoils with β=15° and 5° was examined to determine the effect of varying sweep. Figures 24 and 25 present the cavity appearance on these hydrofoils for attack angles of 2° and 5°, respectively. At the low attack angle, a clear cavity can be seen on the 15° swept hydrofoil near the upstream leading edge. Large portions of the cavity are a vapor/liquid mixture, which is similar to the

Figure 24: Effect of sweep angle at α=2°. β=15°, (a) U=9.2 m/s, σ=0.9 (b) U=9.7 m/s, σ=0.8. β=5°, (a) U=9.6 m/s, σ=1.0 (b) U=9.5 m/s, σ=0.8.
cavities on the two-dimensional hydrofoil. At the higher attack angle, closed cavities were not observed. For the β=5° hydrofoil, closed cavities were not observed for any of the test conditions. The cavities were all similar to those observed on the two-dimensional hydrofoil.
5. CONCLUSIONS
Attached cavitation on both two- and three-dimensional plano-convex hydrofoils was examined. For moderately large attack angles, a region of flow separation exists near the hydrofoil’s leading edge. With a reduction in cavitation number, an attached cavity forms within the separation bubble.
For the two-dimensional hydrofoil, all of the partial cavities were open, and the closure of the cavity was unsteady. Cavitating vortical structures were shed from the attached cavity. At low attack angles, the cavity length and thickness would extend beyond the original non-cavitating separation bubble, and the flow in the cavity wake was not observed to circulate (i.e. no upstream flow vectors were measured). However, at larger attack angles, the partial cavities were contained within the separation bubble, and recirculation was observed downstream of the cavities.
The constant growth and shedding of developed two-dimensional cavities has been associated with re-entrant flow in the cavity closure. Impingement of this flow on the cavity interface causes the break-off of vapor-filled vortices. High momentum re-entrant flow can cause cavity break-off near the cavity detachment line, while low momentum re-entrant flow can lead to the break-off of smaller cavities closer to the cavity closure. However, re-entrant flow was not observed downstream of thin partial cavities. If such a flow exists, it is within the bubbly portion of the cavity. Recirculating flow was observed downstream of cavities which formed within a large region of flow separation. It is possible that a portion of this recirculating flow contributes to a re-entrant flow within the cavity.
Attached cavitation on a series of three-dimensional hydrofoils was also examined. These hydrofoils were plano-convex hydrofoils, but with varying degrees of sweep. A separation bubble was observed near the leading edge of the hydrofoils, although the shape and flow unsteadiness varied along the foil span. As the cavitation number was decreased, the attached cavity formed within this separation bubble, although the cavity might not have spanned the entire hydrofoil. The topologies of the cavities that formed on the swept hydrofoils were often substantially different from those of the cavities formed on the two-dimensional hydrofoil under similar freestream conditions and attack angle. A significant portion of the cavity was vapor-filled, and the re-entrant flow was seen within the cavity. These portions of the cavity were closed, and the flow in the closure region was steady. Other parts of the cavity could be filled with a vapor/liquid mixture, and these regions often coincided with the position of re-entrant flow impingement on the cavity surface. As the sweep angle was decreased, the attached cavitation approached the form found on the two-dimensional hydrofoil for similar test conditions.
The introduction of three-dimensionality to the attached cavity results in the redirection of the re-entrant flow in the cavity closure. As discussed by de Lange [5], the re-entrant flow can be “reflected” in the span wise direction, and this was observed to occur in many of the three-dimensional cavity flows. For large portions of the cavity, the re-entrant flow would not interfere with the development of a steady vapor-filled cavity with a clear interface. In this case, a closed cavity would form, and the profiles of the closed cavities were qualitatively similar to those predicted by two-dimensional free-streamline theory with a re-entrant flow closure.
We conclude with the following observations:
-
The inception and topology of attached cavitation can be strongly related to the topology of the noncavitating flow, especially when large regions of non-cavitating flow separation exist near the region of cavity inception.
-
The unsteadiness in the closure of two-dimensional cavities can be related to the unsteadiness in the non-cavitating separated flow and the continual mixing of re-entrant flow with cavity contents.
-
Closed vapor-filled cavities were formed when the re-entrant flow was directed in the spanwise direction. The cavity would open when the re-entrant flow impinged on the cavity interface.
Finally, we comment that a complete understanding of the dynamics of attached cavitation must include characterization of the flows both outside and within the cavity.
ACKNOWLEDGMENTS
We would like to thank Prof. Joseph Katz for making available to us the fluorescent particles used in the PIV. This work is being supported under the Office of Naval Research contract number N00014–96–1–0076, Dr. E.P.Rood, technical monitor.
REFERENCES
1. Arakeri, V.H., 1975, “Viscous Effects on the Position of Cavitation from Smooth Bodies,” J. Fluid Mech, 68, pp. 779–799.
2. Avellan, F., Dupont, Ph., and Rhyming, I.L., 1988, “Generation Mechanism and Dynamics of Cavitation Vortex Downstream of a Fixed Leading Edge Cavity,” Proc. 17th Symp. on Naval Hydrodyn., The Hague.
3. Bark, G., 1985, “Development of Distortions in Sheet Cavitaiton on Hydrofoils,” ASME Intl Symp-Proc. Jets and Cavities, pp. 215–225.
4. Crimi, P., 1970, “Experimental Study of the Effects of Sweep on Hydrofoil Loading and Cavitation,” Journal of Hydraulics, 4, No. 1, pp. 3–9.
5. de Lange, D.F., 1996, “Observation and Modeling of Cloud Formation Behind a Sheet Cavity” Ph.D. Thesis, University of Twente, The Netherlands.
6. Franc, J.P, and Michel, J.M., 1985, “Attached Cavitation and the Boundary Layer: Experimental Investigation and Numerical Treatment,” J. Fluid. Mech., 154, pp. 63–90.
7. Furness, R.A., and Hutton, S.P, 1975, “Experimental and Technical Studies of Two-Dimensional Fixed-Type Cavities,” J. Fluids Eng., 97, pp. 515–522.
8. Hart, D.P, Brennen, C.E., Acosta, A.J., 1990, “Observations of Cavitation on a Three Dimensional Oscillating Hydrofoil,” ASME Cavitation and Multiphase Flow Forum, FED-98, pp. 49–52.
9. Ihara, A., Watanabe, H., Shizukuishi, S., 1989, “Experimental Research of the Effects of Sweep on Unsteady Hydrofoil Loadings in Cavitation,” J. Fluids Eng., 111, pp. 263–270.
10. Kawanami, Y., Kato, H., Yamaguchi, H., Tanimura, M., Tagaya, Y., 1997, “Mechanism and Control of Cloud Cavitation,” ASME, J. Fluids Eng., 119(4), pp. 788–795.
11. Kawanami, Y., Kato, H., Yamaguchi, H., 1998, “Three-Dimensional Characteristics of the Cavities Formed on a Two-Dimensional Hydrofoil,” Proc. of the Third International Symposium on Cavitation, April 1998, Grenoble, France, pp. 191–196.
12. Knapp, R.T., Daily, J.W., and Hammit, F.G., 1970, “Cavitation,” McGraw-Hill.
13. Kubota, A., Kato, H., Yamaguchi, H., and Maeda, M., 1989, “Unsteady Structure Measurement of Cloud Cavitation on a Foil Section Using Conditional Sampling Techniques,” J. Fluids Eng., 111, pp. 204–210.
14. Laberteaux, K.L, Ceccio, S.L., Mastrocola, V.J., Lowrance, J.L., 1998, “High Speed Digital Imaging of Cavitating Vortices,” accepted for publication, Experiments in Fluids.
15. Laberteaux, K.L, Ceccio, S.L., 1998, “Flow in the Closure Region of Closed Partial Attached Cavitation,” Proc. of the Third International Symposium on Cavitation, April 1998, Grenoble, France, pp. 197–202.
16. Larrarte, F., Pauchet, A., Bousquet, P., Fruman, D.H., 1995, “On the Morphology of Natural and Ventilated Cavities,” Proc. ASME Symp. on Cavitation and Multiphase Flow , FED-210, pp. 31–38.
17. Le, Q., Franc, J.P., and Michel, J.M., 1993, “Partial Cavities: Global Behavior and Mean Pressure Distribution,” J. Fluids Eng., 115, pp. 243–248.
18. Le, Q., Franc, J.P., and Michel, J.M., 1993, “Partial Cavities: Pressure Pulse Distribution Around the Cavity,” J. Fluids Eng., 115, pp. 249–254.
19. Lush, P.A., Skipp, S.R., 1986, “High Speed Cine Observations of Cavitating Flow in a Duct,” Int. Journal of Heat Fluid Flow, 7, pp. 283–290.
20. Maeda, M., Yamaguchi, H., Kato, H., 1991, “Laser Holography Measurement of Bubble Population in Cavitation Cloud on a Foil Section,” Proc ASME Cavitation ’91, FED-116, pp. 67–75.
21. Periera, F., 1997, “Prédiction de L’Érosion de Cavitation: Approche Énergétique,” Ph.D. Thesis, École Polytechniques Fédérale de Lausanne, Lausanne, EPFL.
22. Reisman, G.E., Brennen, C.E., 1996, “Pressure Pulses Generated by Cloud Cavitaiton,” Proc. ASME Symp. on Cavitation and Gas-Liquid Flows in Fluid Machinery and Devices, FED-236, pp. 319–328.
23. Tassin, A.L., Li, C.-Y, Ceccio, S.L., and Bernal, L.P., 1995, “Velocity Field Measurements of Cavitating Flows,” Exp. in Fluids, 20, pp. 125–130.
24. Tassin-Leger, Α., Ceccio, S.L., 1998, “Examination of the Flow Near the Leading Edge of Attached Cavitation: Part 1—Detachment of Two-Dimensional and Axisymmetric Cavities,” accepted for J. Fluid Mech.
25. Tassin-Leger, Ceccio, S.L., Bernal, L.P., 1998, “Examination of the Flow Near the Leading Edge of Attached Cavitation: Part 2—Incipient Breakdown of Two-Dimensional Cavities,” accepted for J. Fluid Mech.
26. Thwaites, B., 1960, “Incompressible Aerodynamics: An Account of the Theory and Observation of the Steady Flow of Incompressible Fluid Past Aerofoils, Wings, and Other Bodies,” Dover Publications, Inc., New York, 1960, p. 101.
27. Yu, P.-W, 1995, “Experimental and Numerical Investigation of Cavitating Flows” Ph.D. Thesis, University of Michigan, Ann Arbor, Michigan.
Numerical Simulation of Evolution of Three-Dimensional Bubbles
Q.X.Wang, E.K.Png, B.H.Tan (DSO National Laboratories, Singapore)
Abstract. Three dimensional bubble evolution is investigated numerically based on the theory of incompressible potential flows. Motion is considered for two adjacent gas bubbles beneath a free surface and a gas bubble near an inclined wall in the gravity field. The present numerical method is characterised in the calculations of the normal vector and tangential velocity vector at a node, the calculation of the solid angles and the influence coefficients, and the boundary triangulation, etc. Comparisons between the results of the present 3D model to a validated axis-symmetrical bubble code are done for a gas bubble near a horizontal wall and a gas bubble beneath a free surface in the gravity field. The comparisons demonstrate the robustness and accuracy of the present method. Simulations at high resolution are performed for two adjacent gas bubbles beneath a free surface and a gas bubble near an inclined wall in the gravity field. The former is equivalent to a gas bubble with buoyancy in the neighbourhood of a free surface and a vertical wall that has not been studied yet in the previous publications. Some flow features are noticed and analysed for this phenomenon.
1. Introduction
Bubble dynamics has significant applications in studying the damage caused to hydraulic machinery by cavitation bubbles and the intentional damage inflicted on marine vessels by underwater explosions. It has long been an important research field ever since the end of last century. Typically, a bubble remains approximately spherical during its expansion and the early stage of collapse. After that, a part of the bubble surface becomes flattened and this perturbation from spherical shape grows rapidly. As the results, the bubble becomes a kidney shape and a high-speed liquid jet is formed within a very short period. The evolution of a bubble is a kind of violent surface motion.
In the last two decades, most successful numerical models of bubble dynamics have been based on time integration coupled with a boundary-integral spatial solution, i.e. Euler-Lagrange method. It was used to simulate the motion of bubbles near a rigid wall by Guerri, Lucca & Prosperetti (1981), Blake, Taib & Doherty (1986), and Best & Kucera (1992), etc. It was also employed to simulate the interaction of a bubble with a nearby free surface by Blake & Gibson (1981), Blake et al. (1987), and Wang et al. (1996a, b).
The studies mentioned above were concerned only with the axis-symmetrical cases. However, there are a few works that utilised 3D boundary integral method to simulate the motion of a bubble near an inclined wall or a structure (Chahine & Perdue, 1988; Wilkerson, 1989; Chahine, 1990, 1993; Harris, 1992, 1993; Blake et al., 1995). The bubble surface was represented by means of planar triangular facets with linear distributions of the velocity potential ![]() and normal velocity component
and normal velocity component ![]() over each element. Time stepping of the bubble surface and velocity potential on it is carried out using Lagrange’s method.
over each element. Time stepping of the bubble surface and velocity potential on it is carried out using Lagrange’s method.
A noticeable feature of boundary integral method on free surface problems is the loss of surface smoothness as the free surface undergoes large deformations. Such numerical instabilities may occur in two-dimensional, axis-symmetrical and three-dimensional cases. In two-dimensional and axis-symmetrical cases, the standard smoothing formula (Longuet-Higgins & Cokelet, 1976; Dold, 1992) is used to overcome the numerical instabilities (Blake et al., 1986 and 1987, Best & Kucera 1992). In 3D cases, the same smoothing technique can be employed for a structured mesh in each isoparametric direction successively (Ferrant, 1996). However this technique cannot be applied for an unstructured mesh such as triangulation. The
kind of numerical instabilities is usually more severe for a finer mesh or a collapsing bubble with a sharp jet. For this reason, most numerical simulations were restricted to low resolution meshes (such as Chahine et al., 1988, 1990, 1993; Wilkerson, 1989; Harris, 1992, 1993), and their simulations often broke down in the process of the jet development. The more recent numerical simulation by Blake, et al. (1995, 1997) could last longer but still broke down at the later stage of the collapse phase. It remains a challenge to formulate a stable numerical algorithm to simulate bubble evolution.
This paper aims to formulate a stable and high-resolution numerical algorithm for 3D bubble motion. The mathematical modelling was outlined briefly in Section 2, which also stated down the basic notation and definitions. The numerical implementation is outlined in Section 3. The detailed numerical procedure can be found in Wang (1998). The present 3D algorithm was compared to a validated axis-symmetrical bubble model of Wang et al. (1996a, b; 1998) for axis-symmetrical cases in Section 4. The evolution of a gas bubble with buoyancy near an inclined wall was investigated in Section 5. The interaction of two adjacent gas bubbles with buoyancy and a free surface was simulated and analysed in Section 6. The evolution of the two gas bubbles and free surface was analysed.
2. Mathematical formulation
Consider the evolution of two gas bubbles below a free surface as shown in Fig. 1. Assume both bubbles are initiated simultaneously as tiny high-pressure spherical bubbles at the same distance h from the initially quiescent free surface (along z=0). The distance of the two bubble centres at initiation is denoted as 2d. This case is equivalent to a gas near a vertical rigid wall and free surface, i.e. a gas bubble near a vertical bank.
The pressure inside each gas bubble comprises two parts: the pressure of the vapour from the surrounding liquid and the pressure of the non-condensing gas. Assuming that the non-condensing gas is ideal and its expansion and compression are adiabatic, the gas pressure pb inside the bubble can be expressed in terms of its volume V as
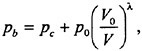
(1)
where V0 is the volume of the bubble at which the particular pressure due to the non-condensing gas would be p0; λ is the ratio of the specific heats. We take λ=1.25 in this work.
A system of non-dimensionalization is adopted here in which all the parameters are scaled with respect to the maximum bubble radius Rm for lengths; the pressure difference Δp=p∞−pc for pressures (where p∞ is the hydrostatic pressure at the level of the bubble centre at the initiation); the liquid density ρ for densities. Rm is the maximum radius that the bubble would attain in an infinite fluid domain at the uniform pressure of p∞.
The fluid in the time-varying fluid domain Ω (Fig. 1) is assumed to be inviscid, incompressible and the flow irrotational. The velocity potential ![]() is governed by the Laplace equation
is governed by the Laplace equation
(2)
The velocity field is given by ![]() . The velocity potential
. The velocity potential ![]() satisfying eq. (2) can be represented in terms of the integral over the boundary ∂Ω as follows
satisfying eq. (2) can be represented in terms of the integral over the boundary ∂Ω as follows
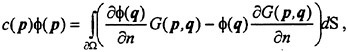
(3)
where G(p, q)=1/|p−q| is the Green function due to a unit source in an infinite fluid; c(p) is the solid angle under which the fluid domain Ω is viewed from the field point p; ∂/∂n=n · ∇ is the normal derivative at the boundary ∂Ω where n is the outward normal of the fluid domain Ω (See Fig. 1). For a bubble near an inclined wall, G(p, q) is the Green function due to a unit source in an infinite fluid domain and an equal source at the image point about the rigid wall.
The motion of the two bubble surfaces S1, S2 and free surface F are governed by the kinematic and dynamic boundary conditions on them defined as follows
(4a)
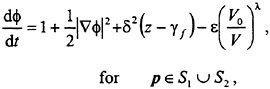
(4b)
(4c)
where δ=(ρgRm/Δp)1/2 is a non-dimensional parameter characterising buoyancy; ε=p0/Δp the non-dimensional initial pressure of the bubble; γf=h/Rm the non-dimensional distance from the bubble centre to the free surface at the initiation. These equations are nonlinear and time-dependent.
Eqs. (3) and (4) form a complete set of equations for the motion of the two gas bubbles and free surface. The bubble is assumed to begin its existence as a tiny high-pressure spherical bubble of radius R0 with any initial radial velocity. During the early phase of the bubble motion, the buoyancy and boundary effects are relative trivial due to their small size, therefore the bubble motion can be described by the Rayleigh equation
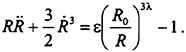
(5)
Given an initial non-zero radial velocity, we may integrate (5) backward in time to obtain the new initial radius and pressure (new value of ε). Thus the freedom of choice of the combinations of the initial pressure and radial velocity is superfluous. Following the work by Best et al. (1992), eq. (5) is solved to determine the initial radius R0 with zero radial velocity and a prescribed strength ε. The initial radius R0 with zero radial velocity is the start state for the numerical simulation.
3. Numerical modelling
Initial mesh
The discretization of the first level of the initial spherical bubble is based on an icosahedron. This shape consists of 20 equal-sized equilateral triangles and 12 nodes all of which lie on the surface of a sphere. This mesh can be improved by breaking each of the original triangles into smaller equal-sized equilateral triangles and projecting them onto the spherical surface. The number of the subdivisions of each of the original triangles defines the “level” of the mesh. For the n-th level mesh each original triangle of the icosahedron is replaced with n2 smaller equal-sized triangles. The arbitrary level triangulation of a spherical surface has been built using the above method. Since the triangulation is an unstructured mesh, the connectivity of the mesh has also been built. The triangulation of the first level and 8-th level of a sphere are shown in Fig. 2.
For a case of bubbles near a free surface, the free surface has to be triangulated too. The free surface triangulation is obtained by projecting the nodes on the upper half of a triangulated sphere to a horizontal plane surface above the sphere. The range and density of the mesh of the free surface is controlled by varying the distances of nodes of every ring to the centre of the meshed region of the free surface. The series of radius of the nodes on ring l (numbering from the centre) are given as following:
(6)
where a is chosen as 1.0 for the case of a bubble beneath a free surface and as 1.2 for the case of two bubbles beneath a free surface; θ is the azimuth coordinate of the polar system with the origin at the centre of the meshed region. An example level 16 triangulation of the free surface with a=1.2 is shown at Fig. 3.
Influence coefficients & solid angles
To calculate the influence coefficients, a local normalised oblique coordinate system (ξ, η) is introduced on each triangle. Locally linear representations of the geometry, potential and normal velocity component ![]() on a triangle are used. The first integration in eq. (3) on a triangle ABC can be expressed as follows:
on a triangle are used. The first integration in eq. (3) on a triangle ABC can be expressed as follows:
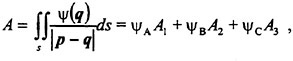
(7)
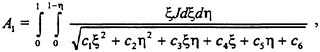
(8a)
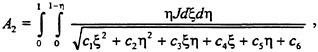
(8b)
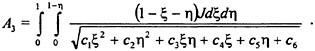
(8c)
with
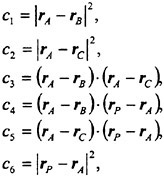
(9)
(10)
where the subscripts A, B and C denote the quantities associated with the vertices A, B and C of the triangle ABC respectively.
The other integration in equation (3) on a triangle ABC can be expressed as follows:
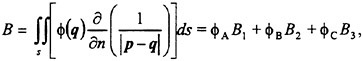
(11)
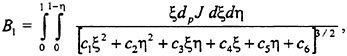
(12a)
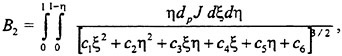
(12b)
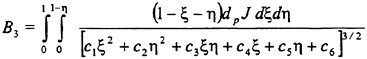
(12c)
where dp=n · (rP−rA), n is the out normal vector of the flow domain on the triangle ABC.
The calculation of the influence coefficients constitutes a substantial part of the total CPU time for the BIM modelling. In this paper, the non-diagonal elements of the influence coefficient matrix are also calculated using a 7-point Gaussian quadrature specifically developed for triangles, which does not bias the integral calculation in any direction. The weights and nodes of this Gaussian quadrature can be found in some finite element textbooks (e.g., Bathe, 1982; Hughes, 1987). The diagonal elements of the influence coefficient matrix are integrated analytically.
For a field point p on the bubble, the solid angle c(p) is available as a subset of the influence coefficients B from the source points on the bubble (Wilkerson, 1989), as the bubble is a closed surface. Since the free surface is an open surface, c(p) on it has to be calculated directly. In the present work, c(p) on the free surface is computed based on the theory for spherical triangle or polygon.
Normal vectors and tangential velocity vectors at nodes
The normal vector at a node is required while updating the bubble shape. But a node is a corner of the boundary after it being meshed into planar triangular facets. Chahine & Perdue (1988) and Chahine (1990, 1993) calculated the two nodal vectors by interpolating locally the bubble surface and velocity potential on it using quadratic polynomials. More recently, Blake et al. (1995, 1997) interpolated locally the bubble surface and velocity potential on it in terms of radial functions. The high order local surface fitting is not unique with the random choice of the functions and neighbouring nodes for the interpolations. A surface fitting is usually suitable for curtain kind of surfaces. It is hard to provide a local surface fitting for arbitrary surface for bubble evolution.
In the present work, the normal vector at a node is calculated by averaging the normal vectors of the surrounding elements. The weighting parameters for the averaging are chosen as the inverse values of the distances between the surrounding element centroids to the node. The tangential velocity vector on a triangular element can be calculated by a finite element technique (Desai & Abel, 1972). The tangential velocity vector at a node is calculated by averaging the tangential velocity vectors on the surrounding elements in the same way as that for the normal vector at a node.
Solver for linear algebraic equations
The linear algebraic equations discretized from the boundary integral equation (3) are solved with direct solvers in the previous simulations mentioned possibly for preventing the numerical instabilities. In the present work, both of the Gauss-Jordan elimination method and the Gauss-Seidel iteration method have been used to solve the linear algebraic equations. Comparisons of the results of the two methods have shown that the iteration method is accurate enough for the numerical modelling and it converges fast and saves CPU time dramatically.
Time updating of free surface
The time integration of the equations (4) are carried out using the predictor-corrector scheme. A bubble usually evolves fast during the early expansion phase and the later collapse phase and slowly around its maximum volume. Therefore, a suitable non-uniform time-step size Δt should be chosen so that it is small when the bubble evolves fast and is large when the bubble evolves slowly. In the present paper the time-step size Δt is chosen as
(13a)
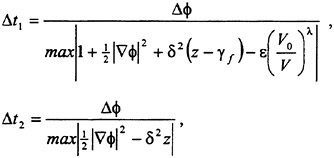
(13b,c)
where ![]() is some constant. The maximum in (13b) is obtained over all nodes defining the bubble surfaces, while that in (13c) over all nodes defining the free surface. This ensures that the maximum change in the velocity potential on the boundary is
is some constant. The maximum in (13b) is obtained over all nodes defining the bubble surfaces, while that in (13c) over all nodes defining the free surface. This ensures that the maximum change in the velocity potential on the boundary is ![]() . The results in this work are obtained with
. The results in this work are obtained with ![]() kept to around 0.03.
kept to around 0.03.
4. Validation
The numerical convergence of the present method has been confirmed by testing with various mesh sizes and time steps. The results have been found to agree well with the Rayleigh solution for a spherical cavitation bubble. The results have also been compared with those computed by a validated axis-symmetrical bubble model (Wang 1996 a, b, 1997) for two axis-symmetrical cases. We will only describe the comparisons with the axis-symmetrical code.
The first comparison is a gas bubble with ε=100 and δ=0.5 above a horizontal wall. The bubble is initiated at γr=1.0, where γr is the dimensionless distance between the centre of the initial bubble and the wall. The bubble shapes of this case are shown in Fig. 4 where a is for the 3D method and b for the axis-symmetrical method. For comparison, the bubble shapes are provided at a same times t (normalised by Rm(ρ/Δp)1/2) for both numerical methods. The time sequence 1 is for the bubble being around its maximum volume, the bubble assumes a ‘strawberry’ shape. The time sequence 2 is at the later stage of the collapse phase. A very sharp upward jet is formed at that time. The numerical model broke down when the distance between the jet front and the opposite bubble surface is of the same order as the element size. One can see that the numerical results of the two methods are in good agreement. All main features were reproduced by the two methods.
The second case is a gas bubble beneath a free surface with ε=100, δ=0.5, γ=0.75. The bubble shapes are shown in Fig. 5a with the results of the 3D model and in Fig. 5b with the results of axis-symmetrical model at same times. The time sequence 1 is around the end of the expansion phase. At that time, the bubble is slightly elongated along the axis of symmetry. The top part of the bubble surface is entrained into the base of the raised free surface thus causing a substantial free-surface hump. The time sequence 2 is at the end of the collapse phase. The bubble jetting is in the downward direction. A tall and sharp spike is formed on the free surface. The simultaneous occurrence of the downward jet and free-surface spike is produced by a high-pressure region between the free surface and the top of the bubble. All the above flow features were reproduced by the two models. Once again the numerical results of the two methods are in good agreement. All main features were reproduced by the two methods
5. A bubble near an inclined wall
To study the motion of a gas bubble adjacent to an inclined wall, simulations were carried out for bubbles with ε=100, δ=0.5 and γr=1.0. Three cases have been investigated: a wall at an angle of 45° to the horizontal under the bubble, a vertical wall adjacent to the bubble, and a wall at 45° to the horizontal above the bubble.
The mottion of the gas bubble above the inclined wall at an angle of 45° to the horizontal is shown in Fig. 6 at selected dimensionless times. The bubble remains roughly spherical for the expansion phase except that the right-lower part of its surface is flattened against the wall at the end of the expansion phase. When the bubble collapses, the flat part of the bubble surface is attracted by the rigid wall, and the rest of the surface migrates upwards due to buoyancy. Consequently, the bubble becomes asymmetric ever since the early collapse
phase (frame 4 in Fig. 6). An upward liquid jet inclined slightly to the right is formed during the collapse phase. The numerical method broke down when a part of the jet surface impacts on the opposite bubble surface (frame 8 in Fig. 6).
The motion of the gas bubble adjacent to the vertical wall with time is shown in Fig. 7. The bubble migrates upward and slightly toward the rigid wall during its expansion phase. The right part of the bubble surface close to the wall is pressed by the wall in the later stage of the expansion phase. During the collapse phase, the left part of the bubble surface migrates upwards faster than the right part which is being attracted by the wall. An upward liquid jet inclined slightly to the wall is formed later. This jet becomes wide and large at the end of the collapse phase. The whole bubble migrates upwards as it collapses.
The motion of the gas bubble below the inclined wall at an angle of 45° to the horizontal is shown in Fig. 8. The bubble migrates in the upper-right direction as expected as it expands. The upper-right part of the bubble surface has been oppressed by the wall ever since the middle stage of the expansion phase; and a large part of the bubble surface over there is flattened against the wall at the end of its expansion phase. An upward liquid jet formed during the collapse phase, and it becomes wide and large at the end of the collapse phase. This jet will impact upon the wall as soon as it penetrates the bubble. The bubble obviously migrates upwards during the collapse phase.
The buoyancy force and Bjerknes attraction are close to each other in magnitude for the above three cases (γδ=0.5), but the jet directs roughly upward rather than close to the bisector direction of the two forces.
6. Two bubbles beneath a free surface
Consider two identical gas bubbles with ε=100 and δ=0.5 initiated simultaneously at a same depth beneath a water surface. The dimensionless distance between the centres of the two bubbles is 2.0. Three cases were simulated for the dimensionless depth of γf=1.5, 1.0 and 0.75. The shapes of the gas bubbles and free surface at selected times t for the three cases are shown in Figs. 9, 10, and 11, respectively.
For the case of γf=1.5, the two bubbles are initiated at 1.5 Rm from the free surface (Fig. 9). The bubbles remain spherical at the early stage of the expansion phase. The adjacent bubble surfaces press against each other and are flattened at the later stage of expansion phase (sequence 3). Around the middle stage of the collapse phase, the lower-left part of the right bubble surface and the corresponding part of the left bubble surface are flattened (sequence 5). Two jets are formed over there subsequently (sequence 6). The jet of the right bubble is in the upper-left direction, and the jet of the left bubble diverts to the upper-right. The free surface is pushed up by the two bubbles during the expansion phase and falls slightly during the collapse phase. A free surface plateau forms above the two bubbles ever since the later stage of the expansion phase.
For the case of γf =1.0, the two bubbles are initiated at 1.0 Rm from the free surface (Fig. 10). The bubbles become elongated vertically in the later stage of the expansion phase (sequence 3). The upper parts of the two bubbles entrain into the base of the raised free surface. Around the middle stage of the collapse phase, the upper-left part of the right bubble surface and corresponding part of the other bubble surface are flattened (sequence 5). The bubbles assume oblate shapes at the end of the collapse phase due to the oppression of the upward buoyancy and downward Bjerknes effect of the free surface. A downward weak jet for each bubble is formed due to the Bjerknes effect of the free surface (sequence 6).
For the case of γf=0.75, the two bubbles are initiated at 0.75 Rm from the free surface (Fig. 11). The two bubbles are elongated vertically ever since the middle stage of the expansion phase (sequence 2). Substantial part of the bubble surfaces entrain into the base of the raised free surface at the end of the expansion phase. The free surface is pushed up much higher than the two earlier cases. There are two large free surface bumps above the two bubbles at the end of the expansion phase. Two jets start at the early stage of the collapse phase at the upper part of the bubble surfaces (sequence 5). These two jets are quite large at the end of the collapse phase. While the tops of two bubbles moves down forming two large jets, the regions of the free surface above the two bubbles rises continuously and all other parts of the free surface fall, resulting in two free-surface spikes (sequence 6).
As compared to the case of a single bubble near a free surface with corresponding parameters as shown in Fig. 5, the maximum height of the free surface plume of the two-bubble case (or a bubble near to a free surface and a vertical wall) is lower. The mechanism underlying the phenomenon can be explained as follows. For the axis-symmetrical case,
fluid is drawn rapidly into the region between the free surface and the top of the bubble during the collapse phase. A stagnation point is formed along the axis of symmetry of the flow configuration. This leads to the formation of a high-pressure region there, which redirects the incoming flow from the sides downward to form the downward Bjerknes jet and upward to form the free-surface spike simultaneously. For a bubble near a free surface and a vertical wall, fluid is also drawn into the region between the free surface and the top of the bubble during the collapse phase. But less fluid from the wall side is drawn into the region as compared to that of the open side. The stagnation point shifts towards the wall, and the high-pressure region around the stagnation point is not as strong as the case without the wall. Thus the corresponding water plume and bubble jet are weaker.
7. Summary and conclusions
The nonlinear evolution of 3D gas bubbles has been investigated numerically based on a time-integration boundary integral method. The present numerical method is characterised by the implementation of the following numerical techniques. The triangulation of arbitrary level of an initial spherical bubble is built based on an icosahedren. The high quality triangulation of the water surface is built based on the projection of a half of the triangulated sphere to a plane. The influence coefficients are calculated using an accurate and efficient hybrid method. The solid angles are calculated using theory of spherical triangles. The normal and tangential velocity vectors at a node are calculated as an average of the corresponding vectors of the surrounding elements. The weighting parameters for the averaging are chosen as the inverse values of the distances from the centroids of the surrounding elements to the node. The linear algebraic equations are solved by an iteration method that saves the CPU requirement dramatically. A predictor-corrector scheme is employed for the time integration.
Detailed comparisons have been carried out between the results of the present 3D algorithm and those by a validated axis-symmetrical bubble code (Wang et al. 1996a, b, 1997) for a gas bubble with buoyancy near an infinite horizontal wall or beneath a free surface. The comparisons demonstrate the robustness and accuracy of the present method.
Simulations were carried out for a gas bubble initiated at 1.0 Rm from an inclined wall with various inclined angles. Simulations were also done for two adjacent gas bubbles below a free surface. Three cases were simulated for both bubbles initiated at 1.5 Rm, 1.0 Rm, and 0.75 Rm from the free surface respectively. The distance between the centres of the initial bubble is 2.0Rm. It is equivalent to the case of a gas bubble initiated at 1.5 Rm, 1.0 Rm, and 0.75 Rm from a free surface and at 1.0Rm from a vertical wall. All the simulations were carried out at high resolution nearly up to the jet impacts on the opposite bubble surface without the numerical instabilities occurring. The following phenomena have been noticed. As comparing to the case of a bubble beneath a free surface, the water plume of the free surface and the bubble jet are weakened by the occurrence of a vertical wall.
Acknowledgement
Thanks to Mr. Peh, K.C. and Mr. Teng, Ν.Η. at the DSO National Laboratories and Defence Research Directorate of Singapore respectively, who supported and assisted in many valuable ways during the course of this research. A part of the research was carried out at the National University of Singapore (NUS) when one of the authors Wang, Q X., was a research fellow there. Insightful and stimulating discussions with Dr. Yeo, K.S., Dr. Khoo, B.C. and Professor Lam, K.Y. of NUS on this research are gratefully acknowledged.
REFERENCES
1. Abramowitz, M. & Stegun, 1965 I.A., Handbook of Mathematical Functions. Dover).
2. Best, J.P. & Blake, J.R. 1994 An estimation of the Kelvin impulse of a transient cavity. J. of Fluid Mech. 261, 75–93.
3. Best, J.P. & Kucera, A. 1992 A numerical investigation of non-spherical rebounding bubbles. J. of fluid Mech. 245, 137–154.
4. Best, J.P. 1993 The formulation of toroidal bubbles upon collapse of transient cavities. J. of Fluid Mech. 251, 79–107.
5. Blake, J.R. 1994 Transient invisid bubble dynamics. The Proc. of the Second
International Symposium on Cavitation (Tokyo), pp. 9–14.
6. Blake, J.R., Boulton-Stone, J.M. and Tong, R.P. 1995 Boundary integral methods for rising, bursting and collapsing bubbles, in H. Power ed., BE Applications in Fluid Mechanics, Computational Mechanics Publications, Southampton.
7. Blake, J.R. & Gibson, D.C. 1981 Growth and collapse of a vapour cavity near free surface. J. of Fluid Mech. 111, 124–40.
8. Blake, J.R., Hooton, M.C., Robinson, P.B. & Tong, R.P. 1997 Collaping cavities, toroidal bubbles and jet impact. Phil. Trans. R. Soc. Lond. A 355, 537–550.
9. Blake, J.R., Taib, B.B. & Doherty, G. 1987 Transient cavities near boundaries. Part 2. Free surface. J. Fluid Mech. 181, pp. 197–212.
10. Blake, J.R., Taib, B.B. & Doherty, G. 1986 Transient cavities near boundaries. Part 1. Rigid boundary. J. Fluid Mech. 170, 479–97.
11. Blake, J.R. & Tong, R.P. 1995 Jet impact in collaping bubbles. In Proc. 12th Aust. Fluid Mech. Conf., Sydney, pp. 819–822.
12. Chahine, G.L. 1990 Numerical modelling of the dynamic behaviour of bubbles in nonuniform flow fields. ASME Symposium on Numerical Methods for Mutiphase Flows, Toronto.
13. Chahine, G.L 1993 Bubble interactions with vortices. In S.Green ed., Vortex Flows, Kluwer Academic.
14. Chahine, G.L. & Perdue, T.O. 1988 Simulation of the three-dimensional behaviour of an unsteady large bubble near a structure. Third International Colloquium on Bubbles and Drops, Monterey, California.
15. Desai, C.S., and Abel, J.F. 1972 Introduction to the Finite Element Method. New York: Van Nostrand Reinhold Comp.
16. Dold, J.W. 1992 An efficient surface-integral algorithm applied to unsteady gravity waves. J. of Comp. Physics, Vol. 103, pp. 90–115.
17. Ferrant, P. 1996 Simulation of strongly nonlinear wave generation and wave-body interactions using 3D MEL model. 21st Symposium on Naval Hydrodynamics (June 24–28, 1996; Trondheim, Norway), Monday Sessions pp. 226–241.
18. Gibson, D.C. & Blake, J.R. 1980 Growth and collapse of cavitation bubbles near flexible boundaries. Proc. 7th Austral. Conf. on Hydraulics and Fluid Mechanics, pp. 283–286. Institution of Engineers, Brisbane.
19. Guerri, L., Lucca, G. & Prosperetti, A. 1981 A numerical method for the dynamics of non-spherical cavitation bubbles. In Proc. 2nd Intl. Colloq. on Drops and Bubbles, pp. 175–181. JPL Publication 82–7, Monterey, California.
20. Harris, P.J. 1992 A numerical model for determining the motion of a bubble close to a fixed rigid structure in a fluid. Int. J. Numer. Methods Eng., Vol. 33, pp. 1813–1822.
21. Harris, P.J. 1993 A numerical method for predicting the motion of a bubble close to a moving rigid surface. Communications in Numerical Methods in Engineering, Vol. 9, pp. 81–86.
22. Longuet-Higgins, M.S. & Cokelet, E.D. 1976 The deformation of steep surface waves on water. I. A numerical method of computation. Proc. R. Soc. Lond. A 350, 1–26.
23. Lundgren, T.S. & Mansour, N.N. 1991 Vortex ring bubbles. J. of Fluid Mech. 224, 177–196.
24. Rogers, J.C. & Szymczak, W.G. 1997 Computations of vilent surface motions: comparisons with theory and experiment. Phil. Trans. R. Soc. Lond. A 355, 649–663.
25. Stroud, A.H. 1971 Approximate calculation of multiple integrals. Prentice-Hall.
26. Wang, Q.X., Yeo, K.S., Khoo, B.C. & Lam, K.Y. 1996 Strong interaction between buoyancy bubble and free surface. Theoret. and Comput. Fluid Dynamics 8, 74–88.
27. Wang, Q.X., Yeo, K.S., Khoo, B.C. & Lam, K.Y. 1996 Nonlinear interaction between gas bubble and free surface. Computers & Fluids V. 25, No. 7, pp. 607–628.
28. Wang, Q.X., Yeo, K.S., Khoo, B.C. & Lam, K.Y. 1998 Toroidal bubbles near a rigid boundary. Theoret. and Comput. Fluid Dynamics, (sent for publication).
29. Wang, Q.X., 1998 The evolution of a gas bubble near an inclined wall. Theoret. and Comput. Fluid Dynamics, (in press).
30. Wilkerson, S.A. 1989 Boundary integral technique for explosion bubble collapse analysis. ASME Energy-Source Technol. Conference and Exhibition, Houston, Texas.
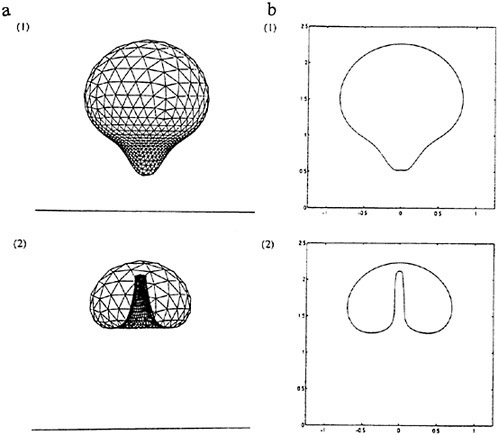
Fig. 4 Evolution of a gas bubble above a wall for ε=100, δ=0.75, γr=1.0: (a) 3D model results, (b) axisymmetrical model results. The dimensionless times t corresponding to shapes are (1) 2.019, (2) 2.273.
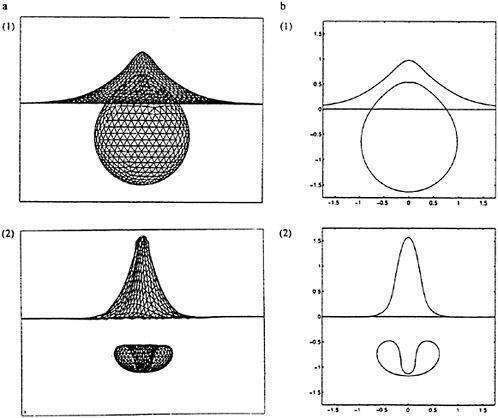
Fig. 5. Evolution of a gas bubble beneath a free surface for ε=100, δ=0.5, γf=1.0: (a) 3D model results, (b) axisymmetrical model results. The times t corresponding to successive shapes are (1) 0.711, (2) 1.360.
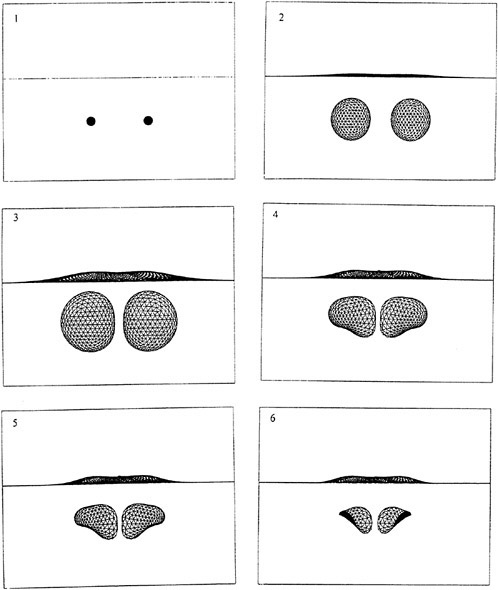
Fig. 9. Evolution of two gas bubbles beneath a free surface for ε=100, δ=0.5, and γf=1.0. The dimensionless distance between the centres of the two bubbles at inception is 2.0. The dimensionless times t corresponding to shapes are (1) 0.000, (2) 0.260, (3) 1.119, (4), 1.565, (5) 1.670 and (6) 1.789.

Fig. 10. Evolution of two gas bubbles beneath a free surface for ε=100, δ=0.5, and γf=1.0. The dimensionless distance between the centres of the two bubbles at inception is 2.0. The dimensionless times t corresponding to shapes are (1) 0.000, (2) 0.236, (3) 1.030, (4) 1.240, (5) 1.450, and (6) 1.562.
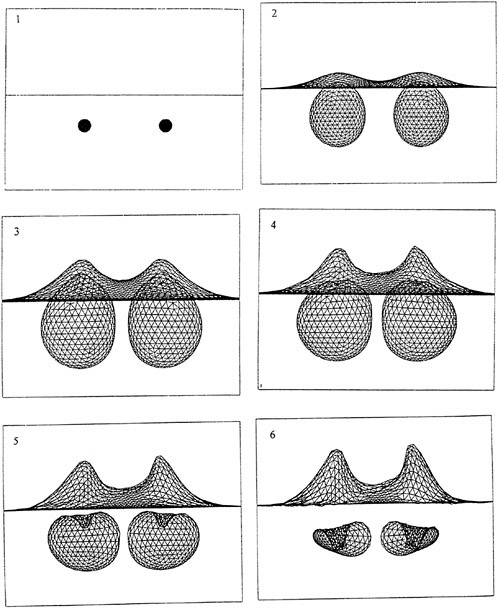
Fig. 11. Evolution of two gas bubbles beneath a free surface for ε=100, δ=0.5, and γf=1.0. The dimensionless distance between the centres of the two bubbles at inception is 2.0. The dimensionless times t corresponding to shapes are (1) 0.000, (2) 0.236, (3) 0.716, (4) 0.939, (5) 1.444, and (6) 1.402.
DISCUSSION
Y.Cao
University of New Orleans, USA
This is an interesting paper. The authors have presented a 3-D numerical method to simulate the dynamics of gas bubbles in a liquid, which is a very difficult problem. For axis-symmetrical case, the results obtained using the 3-D code agree well with those obtained using an axis-symmetrical code.
I have the following comments and questions:
1. The authors use a triangular mesh for the surface discretization. The initial mesh starts with an icosahedron. The icosahedron consists of 20 equal-sized equilateral triangles with all the 12 vertices lying on a sphere. The mesh is refined by farther dividing each triangle into smaller equilateral triangles and projecting them onto the sphere. The process is repeated until the desired resolution is achieved. The connectivity of the mesh is also built during the process. The mesh (e.g., its nodes) is then time-stepped using an Euler-Lagrange’s method. The mesh deforms in the time stepping procedure. However, no regridding of the surface is performed, and the mesh connectivity remains unchanged. As is known, for violent surface motion such as the gas bubble expansion, collapse and water jet formation, the mesh density will change dramatically. This can also be seen in the figures given in the paper. The drastic non-uniform mesh density usually would cause numerical instability and breakdown of simulation. It is surprising that the authors do not seem to have this difficulty in their simulations.
2. For a gas bubble, the bubble surface is continuously smooth until a water jet is formed. Even when the water jet is formed, the surface is not smooth only in a small region near the water jet where the surface slope changes rapidly. Most of the surface remains smooth. As known, for a point on a smooth surface, the theo-retical solid angle is 2π. The numerical solid angle computed based on the discretized surface should not be significantly different from the theoretical value 2π and approaches the theoretical value as the mesh becomes finer. It is my opinion that it is not necessary to replace the theoretical value with the numerical solid. This will represent some CPU time saving. Of course, the actual solid angle should be used where the surface is not smooth and has a shape corner or edge. Have the authors examined the influence of the solid angle on the final results and the CPU time?
3. For the cases with the free surface, the computational free surface domain used seems too small. One would expect a strong non-physical reflection from the free surface truncation unless some sort of open boundary condition (or treatment) is applied. What kind of treatment is used in the paper?
AUTHORS’ REPLY
We would like to thank Dr. Cao for his comments. The authors agree that the numerical instability may happen for the simulation of gas bubble collapse and water jet formulation, as happened in the past studies. However, smooth and stable solutions were obtained in our simulations.
In principle, the solid angle is close to 2π as the mesh becomes very fine. However, the difference between the actual solid angle and 2π may not be small in a discretized modeling. Take a spherical bubble as an example: the difference is about 10% when it is meshed into n=1280 triangles. Its influence on the final results should be of the same order. Moreover, the authors found that the accurate solid angles are crucial for the stability of the numerical modeling. The calcula-tion of solid angles is of O(n) and it is not a substantial part of the CPU time of the modeling.
The computational domain of the free surface was around 10 Rm (maximum radius of the bubble) in radius. Only a small part of the computational domain was shown in the paper. We have compared with a larger computational domain around 15 Rm in radius and found the results agreed up to first four significant figures.
DISCUSSION
K.Thiagarajan
Australian Maritime Engineering, Australia
Viscous effects and surface tension are important considerations when looking at interactions of bubbles with free surface. Do the authors plan to introduce these effects into their simulation program?
AUTHORS’ REPLY
The surface tension may be important for very small bubbles, which can be included in the present program. Because the shear stress between the gas/liquid is much less than liquid/liquid, very little vorticity is produced over there and the flow remains as irrotational. Thus, the viscous effects are small and negligible.
DISCUSSION
U.Bulgarelli
Istituto Nazionale per Studi ed Esperienze di Architettura Navale, Italy
Is there any relationship between the time step and partial steps for stability?
When the bubble increases you put more panel on the surface, you discretize each time of the surface?
When there is a finger in the bubble you lose the existence of the potential as in toroidal bubbles?
AUTHORS’ REPLY
1. In the paper, the time step is controlled by setting a limit for the maximum change in potential on the boundary for each time step. However, the time step may also be controlled by the maximum spatial step of the nodes on the boundary as you suggested, which may be relative to the local element size.
2. The mesh deforms in the time stepping without re-gridding. However, the grids around the jet automatically become dense as required by the modeling.
3. The bubble surface is discretized and described as a set of triangles. We have not used a surface equation to express the bubble surface. Even if there are fingers on the bubble surface, it can be described as a set of triangles. There is no multi-value problem. Whereas, for toroidal bubbles, the flow field is doubly connected. The solution of the Laplace equation in a doubly-connected domain is not unique. Special modeling is needed to make the solution unique (Wang, 1998).
References
Wang, Q.X. 1998. The numerical analysis of the evolution of a gas bubble near an inclined wall. Theoret. and Comput. Fluid Dynamics 12, 29–51.
Wang, Q.X., et al. Toroidal bubbles near a rigid boundary. Theoret. and Comput. Fluid Dynamics (in press).
DISCUSSION
R.Tong
University of Birmingham, USA
The surface shapes are well resolved and the interaction of two bubbles with a free surface is an interesting case. The computation of normal directions and tangential velocities at nodes on the bubble surface is an aspect which requires careful handling. The use of a weighted averaging described in this paper appears to overcome the difficulties which can lead to a breakdown of the solution. There are three areas which I think are worthy of further mention: the particular context for which solutions are sought and the suitability of the boundary integral method (BIM); the underlying rationale for different choices of surface approximation methods and their relationship to the equations being solved; the causes of numerical instabilities in BIM for unsteady interface motion.
The BIM does not allow for the break-up of the bubble surface or for compressible effects in the liquid. For an underwater explosion near a free surface, experiments show the surface breaking into a plume of spray rather than forming a smooth jet and for cases where there is a jet, it is likely that surface tension aids the maintenance of stability. There are thus particular flow regimes where BIM provides accurate information (see Blake et al., 1998) and others where it is not applicable.
The methods of surface approximation chosen depend on the nature of the underlying equation Smoothness of the liquid surface is implied by the BIM formulation and convergence to the smooth surface can be attained as the number of planar elements is increased. Some anomalies occur in the convergence of linear approximations as noted in Blake et al. (1995) and Zinchenko et al. (1997) which should be compared with the method presented in the present paper. It is also possible to improve the
approximation of the surface by using higher order basis functions (see the literature on h-p approximation in Finite and Boundary Elements). The radial functions discussed in Tong (1997) can give spectrally accurate approximation to smooth surfaces which aids computational efficiency and can be necessary for representation of the modes of bubble oscillation.
The occurrence of numerical instabilities in other methods seems exaggerated in the present paper. The breakdown of the computation reported in Blake et al. (1995) in due to the jet tip reaching the opposite bubble surface and the computation goes as far as equivalent axisymmetric cases. Some discussion of the causes of instability is given in Baker & Nachbin (1998).
References
Baker, G. and Nachbin, A. 1998 Stable methods for vortex sheet motion in the presence of surface tension. SIAM J. Sci. Comput. 19, 1737–1786.
Blake, J.R., Tomita, Y., and Tong, R.P. 1998 The art, craft and science of modelling jet impact in a collapsing cavitation bubble. Appl. Sci. Res. 58, 77–90.
Tong, R.P. 1997 A new approach to modelling an unsteady free surface in boundary integral methods with application to bubble-structure interactions. Math. Comput. Sim. 44, 415–426.
Zinchenko, A.Z., Rother, M.A., and Davis, R.H. 1997 A novel boundary-integral algorithm for viscous interaction of deformable drops. Phys. Fluids 9, 1493–1511.
AUTHORS’ REPLY
The free surface breaks into a water spike covered by a spray for an underwater explosion near it. The phenomena cannot be fully simuated by BIM, but it is the first step toward more accurate modeling. For very small bubbles, the surface tension may help to maintain the smoothness of the jet. However, the smooth jet may occur for cases whereby the surface tension is small and negligible. Some examples can be found in the experiments of Blake & Gibson (1981).
A high-order local-surface-fitting is suitable for a surface when the surface-fitting behavior matches with the surface. It is hard to provide a high-order local-surface-fitting that is good for an arbitrary surface. It is hard to compare the interpolation scheme on how accurate they are for an arbitrary shape. Besides, the high order panel methods are known to be more susceptible to numerical instability. Therefore, the authors prefer global linear interpolation coupled with the weighted averaging approach.
The jets were not smooth at the end of collapse phase, and sometimes broke in the middle stage of jetting in the previous simulations (Blake et al. 1995, 1997). In the present work, the smooth jets were simulated nearly until the jet impacts upon the opposite bubble surface. The very sharp jets were simulated in the present work that had not been simulated in the previous papers.
Reference
Blake & Gibson 1981 J. Fluid Mech. 111, 124–140.