APPENDIX
Interactions Between Survey Estimates and Federal Funding Formulas
Alan M. Zaslavsky and Allen L. Schirm
Federal programs that allocate funds to states and localities for the low-income population have typically used estimates from the decennial census in the allocation formula. As one example, the Title I education program historically used census estimates of poor school-age children for allocations; recently, however, the program has used more up-to-date estimates. These estimates are from the Census Bureau 's Small Area Income and Poverty Estimates (SAIPE) Program, which uses data from the March Current Population Survey (CPS), the census, and administrative records in statistical models. Looking to the future, the American Community Survey (ACS), if it is implemented as planned, will be a source of continuously updated estimates from a large sample of households that could be used in allocation formulas.
The introduction of a new data source for the allocation of federal funds to states and localities can affect allocations substantially, for two reasons. First, the new data source may measure a concept differently from previously used sources. For example, the CPS and the decennial census long form find different levels and distributions of poverty (National Research Council, 2000c:Ch.3). Such differences may be consequences of differing survey items, modes of administration, survey protocols, and other details of survey design, and are particular to each survey. Second, even if two surveys provide unbiased estimates of the same quantity, statistical characteristics of the surveys may differ. Among the relevant statistical characteristics are the distributions of errors and the frequency of the survey.
In this paper we consider the second of these issues by drawing out some of the potential implications of introducing a new survey, such as the ACS, for calculation of fund allocations. Our intent is to address some general characteristics of federal funding formulas and the ways in which they might be affected by a shift to a new data source that provides sample data on a continuous basis. We do not attempt to predict the effects of using the ACS on particular units or to assess quantitatively the potential effects of use of the ACS.
We begin by discussing some of the data sources and estimation approaches that are currently used for distribution of federal program funds. We then describe generic features of funding formulas and some potential anomalies inherent in applying the current formulas to sample data. We illustrate these anomalies with simulations. Finally, we argue that when data sources change, properties of the formulas change as well; consequently, consideration should be given to modifying the formulas in light of the original objectives for which they were designed.
Our paper was originally developed for a workshop on the American Community Survey, sponsored by the Committee on National Statistics, in September 1998 (see National Research Council, 2000b). However, the analysis applies not only to the use of estimates from the ACS, but also to the use of estimates from any survey.
DATA SOURCES AND ESTIMATION APPROACHES
Funding formulas typically require estimates of numbers of people who are eligible to receive a benefit distributed through some intervening agency. For example, the number of children in certain age ranges that are in low-income families is required for calculation of grants to states for the Special Supplemental Nutrition Program for Women, Infants, and Children (WIC) or for distribution of Title I education aid. The number of low-income children who are uninsured is required for estimates of need for the State Children's Health Insurance Program (SCHIP) initiative. The fraction of a population that falls into the eligible category may also be important for determining where need is concentrated. Hence, estimates of the total population in a broad category (usually by age, such as the number of children), the number falling into an eligibility category within that population (such as the number of poor children), and the fraction of the population falling into the eligibility category (such as the poverty rate among children) are all potentially of interest.
Estimates of total population are derived from the most recent census, updated to the present year by the use of administrative records. These demographic estimates are subject to some error, especially for relatively small areas and towards the end of the postcensal decade. Still,
comparisons made in the SAIPE program at the Census Bureau suggest that error from this source is smaller than that due to estimation of eligibility rates and numbers (National Research Council, 2000c:Ch.8).
Estimates of eligible population are based on the census, survey data, and possibly auxiliary data sources. Estimation procedures may be simple and direct or quite complex. For example, before the 1997-1998 school year, Title I education funds were distributed to counties on the basis of the last decennial census, and so allocations were only updated once each decade (apart from minor adjustments due to school district boundary changes and updating of the small part of the counts, such as children in institutions for neglected and delinquent children, based on noncensus data). Since then, however, state and county estimates of children in poverty have been estimated using a complex empirical Bayes model fitted to CPS data, in which decennial census estimates appear as a covariate along with income tax poverty and nonfiling rates and numbers of food stamp recipients. (School district estimates are developed by applying the proportions of poor school-age children in each school district within a county from the 1990 census to updated estimates from the county model.)
Even the CPS data that are inputs to the model are not simply annual estimates, but instead are cumulated (averaged) over a 3-year period, centered on the reference year, for the county small-area estimation model. CPS data are sparse for all but the largest states and counties, and the models that are used only imperfectly fit the data. Nonetheless, assessments by the Census Bureau and by the panel (National Research Council, 1998, 1999) concluded that the model-based estimates were on the whole superior to those obtained by simply carrying forward rates or shares from the previous decennial census. (For small domains, such as small counties and school districts, sampling error in census long-form estimates may be substantial, perhaps even larger than model error.) Numbers of WIC eligibles by state are calculated using a similar, although more complex, model.
Among the most important perceived advantages of the ACS is that it will provide a relatively dense sample in each year, bridging the gap between the current census long form, with its dense but temporally infrequent sample, and the CPS and other current surveys, which are collected almost continuously but with relatively sparse samples. This feature offers the possibility of developing current estimates using simple models or cumulation procedures. Depending on the size of the target area (and the sampling rate applied there), ACS estimates may be based on simple cumulation of 1 to 5 years of data.
Aside from the purely statistical advantages of such an approach, it may also achieve superior public acceptability because of its apparently
greater directness. Direct estimates are usually defined as those based only on data collected within the domain for which the estimates are being made; indirect estimates are those that also use data for other domains. Domains may be defined cross-sectionally (as geographical areas or other parts of the population), temporally, or both. Simple indirect estimators may average over spatial domains (e.g., combining several school districts in a county to estimate a single poverty rate that will be used for all of them) or over time (cumulation over years). More complex indirect estimators include the range of small-area estimation models (Ghosh and Rao, 1994), such as synthetic estimation, regression estimation, and hierarchical Bayes models.
The former Title I estimation method using long-form data was direct for the year of the census. (It was temporally indirect when used in later years.) The new estimation procedure, which uses a regression model fit to a national CPS data set, is indirect. The procedure proposed for adjustment of the 1990 census population counts for states was also indirect (Hogan, 1993). Use of an indirect method for such a high-profile objective was evaluated in hindsight by the Census Bureau as too controversial (Fay and Thompson, 1993), and a decision was made to use only direct estimates at the state level in the procedures for the 2000 census (Schindler, 1998). This decision was reversed after use of adjusted counts for congressional apportionment was prohibited, and current plans call for indirect estimation for most domains.
The cumulation procedures proposed for the ACS are at an intermediate level of directness between those used in Title I estimation before and after the shift to model-based estimates. Geographically they are direct, but temporally they are indirect in that current estimates are based on a collection of temporally distinct domains, namely, populations as they were in the same geographic area in previous years. From a purely statistical point of view, both forms of indirectness raise similar issues of model error. Temporal indirectness of the form found in the ACS, however, can hardly be criticized if it replaces the even more indirect procedure of estimating the present situation from a single previous year (the decennial census year) with no current data.
FUNDING FORMULAS
Formulas for distribution of federal funds to states and substate units can be quite complex. A single program may distribute parts of its funds according to several different formulas. Nonetheless, the issues we are concerned with in this paper can be discussed in terms of a few common features.
Funding formulas typically involve distribution of funds in propor-
tion to a measure of need, such as the number of members of a subpopulation that are in poverty by some standard. Generally, the total pie to be divided is determined by the appropriations for the program, although the level of the appropriation may itself be affected by Congress 's perception of total need. Consequently, funding formulas have an aspect of indirectness, in the sense that an increase in allocation to one domain implies a decrease somewhere else, although the effect of each domain's allocation on each other domain is generally small.
Proportional allocation of funds may be modified by hold-harmless provisions and thresholds. A hold-harmless provision limits the amount by which the allocation to a unit can decrease from one year to the next. With a 100 percent hold-harmless provision, no unit's allocation is allowed to decrease. With an 80 percent provision, no unit's allocation may decrease by more than 20 percent in any year. The hold-harmless level may vary from year to year as part of the appropriations process. The hold-harmless level may also depend on some other characteristic of the unit, such as its poverty rate. The rationale for a hold-harmless provision is that it moderates fluctuations in the allocation to each governmental unit, softening the effects of cuts on a unit that has budgeted services in anticipation of an allocation similar to the previous year's. With a high hold-harmless level and static or declining total appropriations, allocations may be essentially frozen regardless of shifts in the distribution of need indicated by more recent data. With growing budgets, the effect of a hold-harmless provision is ameliorated, if the provision is stated in terms of absolute amounts (as is typical), rather than shares of the total amount distributed. For example, if the total budget grows by 5 percent, a 100 percent hold harmless allows a unit's share to fall by almost 5 percent.
A threshold is a minimum level below which a unit is not entitled to receive funds from a program (or a component of a program). A threshold may be an absolute count (e.g., a minimum number of children in poverty) or a rate (e.g,. a minimum poverty rate). A threshold on counts operates to prevent dispersal of funds across small units in which the scale of the local program would be too small to administer effectively or efficiently. A threshold on rates directs funds to units where the relative burden of need is greatest, and the governmental unit is presumably least able to meet it with its own resources.
The allocation provisions described above are illustrated by two important programs: the WIC nutrition program and the Title I compensatory education program. In WIC, allocations are based on state estimates; in Title I, allocations are based on county and school district estimates.
WIC is a federal grant program for states that is administered by the Food and Nutrition Service of the U.S. Department of Agriculture. The
program provides nutrition and health assistance services for low-income childbearing women, infants, and children. The current rule for allocating WIC food funds to states became effective on October 1, 1999, and specifies that if there is sufficient funding, each state receives a grant equal to its final prior year grant. Thus, there is a 100 percent hold-harmless provision. (If there is insufficient funding to give all states their prior year grants, each state's grant is reduced pro rata.) After prior year grants have been provided, up to 80 percent of remaining funds are allocated as inflation adjustments. Then, all remaining funds are allocated based on each state's estimated “fair share,” that is, its share of the estimated national population of persons who are eligible for the program on the basis of income. Thus, a state with 1 percent of the eligible persons has a fair share of 1 percent of the total available funds, and the dollar amount that is 1 percent of the total is the fair share target funding level. States whose prior year grants adjusted for inflation are less than their fair share targets receive “growth funds.” The amount of growth funds received by an “under fair share” state is directly proportional to the difference between the prior year grant adjusted for inflation and the fair share. States with prior year grants adjusted for inflation in excess of their fair share targets do not receive growth funds (unless all the “ under fair-share” states decline to accept the full amount of growth funds available).
States' fair shares are calculated from estimates of the numbers of infants and children in families with incomes at or below 185 percent of poverty, the income eligibility threshold for WIC. Beginning with fiscal year 1995, state allocations have been determined from model-based estimates obtained using CPS, decennial census, and administrative records data (Schirm and Long, 1995); the model was revised for fiscal 1996 (Schirm, 1996) and has undergone further development since then. In prior years (under somewhat different allocation rules), state grants were calculated from decennial census estimates. Estimates from the 1980 census were used from the early 1980s until fiscal year 1994, when 1990 census estimates were used.
Title I of the Elementary and Secondary Education Act provides federal funds to school districts for education programs for disadvantaged children. To date, Congress has appropriated funds for two types of Title I grants, basic grants and concentration grants, which totaled about $7 billion and $1 billion, respectively, for the 1999-2000 school year. Through the 1998-1999 school year, Title I funds were allocated to school districts through a two-stage process; the U.S. Department of Education allocated funds to counties, and states suballocated funds to school districts within each county. Direct allocations to school districts began with the 1999-2000 school year, but we describe here the former system.
Allocations are based on the estimated numbers and percentages of
school-age children who are poor. The rules for allocating funds are complex and include both hold-harmless provisions and eligibility thresholds. For example, a variable hold-harmless rate pertains to basic grants. A school district is guaranteed at least 95 percent of its prior year grant if at least 30 percent of its school-age children are poor. The guarantee falls to 90 percent if the percentage poor is between 15 and 30 and to 85 percent if the percentage poor is below 15.1 To receive basic grant funds, a school district must have at least 10 eligible children who constitute more than 2 percent of the district 's population aged 5 to 17. To receive concentration grant funds, a district must have more than 6,500 eligible children or more than 15 percent of children aged 5 to 17 who are eligible. Further complicating the allocation process, Title I grants also depend on other factors, such as state average per-pupil expenditures.
Model-based estimates of the numbers and percentages of school aged children who are poor in states and counties were first used to allocate Title I funds for the 1997-1998 school year. These estimates were developed by the Census Bureau from CPS, census, and administrative records data. In prior years, direct estimates from the census were used to allocate Title I funds. Recently, the Census Bureau developed model-based estimates for school districts that have been evaluated (National Research Council, 2000c:Ch.7) and were used in allocating funds directly to school districts for the 1999-2000 school year.
INTERACTIONS AMONG DATA SOURCES, ESTIMATION PROCEDURES, AND ALLOCATION FORMULAS
General Findings
Data sources, estimation procedures, and allocation formulas each play a role in the successive steps of calculation of fund allocations. In practice, the distinction between the roles played by the estimation procedure that generates the inputs to the funding formula and the formula itself can be formal and legalistic because the same calculations often may be positioned either in the estimator or in the formula. For example, the law may specify that allocations are based on a 3-year moving average, and that each year's estimate is based on a single year's data. The same effect is obtained, however, if the formula uses a single year's estimate but
|
1 |
For the 1998-1999, 1999-2000, and 2000-2001 school years, Congress has enacted a 100 percent hold harmless for both basic and concentration grants. |
the estimate for that year is calculated (for purely statistical reasons) as a 3-year moving average. For another example, a formula may specify that a school district's eligibility for a category of funds depends on the poverty rate in the district, but if estimates are calculated only for counties and then applied directly to the districts, the effect is the same as if eligibility were calculated at the county level. In that case, developing a capability to estimate poverty rates by district effectively changes the formula. In contrast, some formula provisions do not have natural counterparts in estimation procedures: hold-harmless provisions are common examples.
Keeping this relationship between estimation and formulas in mind, we consider the effect of various choices of formula and estimator under various scenarios for sampling error (determined in part by the size of the domain) and year-to-year patterns in the population value (number or rate) for the target group (e.g., children in poverty). Before setting out detailed scenarios, we note several facts. First, reliance on census data implies that the data will be seriously out of date much of the time. Because of the time it takes to process long-form data, they are about 2 years old by the time they are tabulated, and the reference year of the data is the year previous to the year in which they are collected. Therefore, by the time census data become available, data from the previous census will have been used to allocate funds up to 13 years past the reference year. Analyses of CPS data for Title I allocations suggested that substantial shifts in the geographical distribution of poverty can take place in periods of 3 or 4 years, a finding that should be unsurprising to students of regional business trends. Consequently, reliance on census data implies unresponsiveness to significant short-term regional trends in poverty.
Second, even in terms of long-run averages, reliance on census data is problematical because the census only gives a few widely separated snapshots. For example, over a 30-year period, only three censuses take place, and it would not be surprising if some states happen to have poverty rates at all three censuses that are substantially below their average rates over the 30-year period. Such states would not receive their fair share of allocations, even averaged over the 30-year period. Similarly, a state (or county) could fall below a threshold in a single year that happens to be a census year and, hence, lose its entitlement to funding that it might have obtained if the census had occurred in any other year. In effect, the estimates suffer from small temporal sample size. This problem can be solved only by measuring poverty in more of the intervening years.
Third, the effect of hold-harmless provisions depends on both the frequency with which new data become available and the frequency of reallocation. For example, after new census data become available, shares could be reallocated only once, or they could be reallocated annually,
applying a hold-harmless each year, so that a state whose share has fallen would move to its new share through a series of annual steps. With decennial adjustments of allocations and a fairly high hold-harmless level, it may take several decades for a state with a single spike in its poverty rate to return down to allocations appropriate to its more typical level. With annual adjustments, even with a hold-harmless level very close to 100 percent, the cumulative change in allocations over a decade is likely to be larger: for example, 10 decreases of 7 percent are about equivalent to a single decrease of 50 percent. In practice, hold-harmless levels are decided legislatively. Consequently, the actual effect of changing the schedule of recalculation is unpredictable, because Congress may be influenced by the change in the estimation method to set a different hold-harmless level than it would if allocations were adjusted only after each decennial census. (We point out below that the effect of hold harmless is further complicated by the role of sampling error.)
Fourth, if each year's samples are independent, or almost so as in the ACS, then variances can be reduced by cumulation, that is, by calculation of a moving average. Assuming uncorrelated sampling error with equal variances in each year, using a 3-year equally weighted moving average multiplies variances by a factor of one-third (.333). Less obviously, an exponentially weighted moving average using 3 years of data with weights proportional to 0.70 = 1, 0.71, and 0.72 (at lags 0, 1, 2 years) multiplies variances by a factor of .361, very close to the reduction obtained by equal weighting, while giving greater weight to the most recent data. (The weighting factor of 0.7 might be seen as a compromise value because it reduces the weight on data from 2 years back substantially, to half that of the most recent year, but does not too greatly affect variances.) These results on cumulation do not apply to the CPS because of the positive correlation between annual estimates caused by its rotation group design. Although this design can be exploited to obtain improved estimates of changes, simple cumulation will not reduce variance as much as with an independent design.
Fifth, holding procedures and annual appropriations constant over time, a linear estimation procedure (i.e., a weighted moving average with fixed weights for each lag) combined with a linear formula gives allocations that tend to agree, in the aggregate, with those corresponding to average shares over a long time period. This result follows from the fact that every year is given equal total weight (appearing at each relevant lag) except those close to the beginning or the end of the interval. The premises of this argument are not entirely realistic. Annual appropriations for a program are not constant (in current or constant dollars). Hence, it is inevitable that some states will have the good fortune (or political influence) to be entitled to their largest shares of the pie in the years in which
the pie is largest. Such a state will receive an aggregate share over the period that is larger than the average of its annual shares; conversely, another state will receive a smaller aggregate share. Furthermore, it is not evident that “unbiased” aggregates in this sense are a particularly desirable property from the standpoint of fair or efficient allocation, when needs change from year to year. Nonetheless, this result suggests that some of the complexities of the interaction between the estimation procedures and formula arise because one or both is nonlinear.
Illustrations
We now consider some of the more complex interactions among the elements of the allocation process by developing several illustrative scenarios. We assume that allocation is based on a single variable, which may be interpreted as a standardized poverty rate, set on a scale (for simplicity of presentation) for which a typical value is about 1.
We ignore the dependence of allocations on levels in other domains. In practice, each domain is affected by the others because they share a prespecified total appropriation, but this is not important to the illustrations in this section, in which we focus on the differential effects on different units. In the next section, we show more rigorously how this form of dependency among domains affects our results.
We simulate annual reallocations over a 4-year period. Each scenario is defined by four elements, drawn from a set of alternatives: sampling standard deviation, estimation method, formula, and population process.
-
The sampling standard deviation assumes one of four values: 0.1, 0.25, 0.5, and 1.0. These values may be regarded as corresponding to a moderately large domain, mid-sized domains, and a small domain, defined in terms of sample size. We also consider a domain with no sampling variance, representing a very large domain, as a standard of comparison. We assume that sampling error is normally distributed with a mean of zero. (This is a reasonable approximation for small values of the sampling standard deviation, but not for a value of 1, for which normality would imply a substantial probability of a negative estimate of the rate.)
-
The estimation method is a single-year estimate (SINGLE), a 3-year moving average with equal weights (MA3), or a 3-year moving average with weights proportional to 0.70, 0.71, and 0.72 (MAE3).
-
The formula has four possibilities: allocation is equal to the standardized poverty rate (PROP); allocation is equal to the rate with an 80 percent hold-harmless provision (HH), meaning that the allocation is the maximum of the current rate and 80 percent of the last allocation; allocation is equal to the rate if it is above a threshold of 1 and 0 if it is below 1
-
(THRESH); combination of threshold and hold harmless, equal to the maximum of the current rate (or 0, if the current rate is less than 1) and 80 percent of the last allocation (HH-THRESH). In any case we assume that the hold harmless does not affect allocations in the first year.
-
For the population process, the population standardized poverty rate is either constant (CONS) at one of several rates, trending upward from .75 to 1.25 (UP) over a 4-year period, or trending downward from 1.25 to .75 (DOWN).
Rather than simulating all possible combinations of these factors, we focus on a few sets of scenarios to illustrate specific points. In many of our simulations, we emphasize the effect of sampling variability on the expected allocation for an area under a particular scenario. Because sampling variability is so much affected by the size of the domain, this approach focuses attention on possible inequities to large or small domains that are otherwise similar—that is, the tendency for one or the other type of domain to systematically obtain disproportionately smaller allocations for a given trajectory of population rates.
Scenario 1: Effects of Sampling Variability with a Threshold
Table A-1 illustrates the effect of sampling variability when there is a threshold and each year is estimated independently (SINGLE, THRESH, CONS, with constant true rates 1.3, 1.1, 0.9, or 0.7). The entries are expected values (averaging over the sampling distribution of the estimates).
TABLE A-1 Results for Scenario (1): Effects of Sampling Variability with a Threshold, Single-Year Estimator
|
True Standardized Poverty Rate |
1.3 |
1.1 |
0.9 |
0.7 |
|
Sampling Standard Deviation (SD) |
Expected Allocation |
|||
|
SD = 0 (exact) |
1.30 |
1.10 |
0.00 |
0.00 |
|
SD = 0.1 |
1.30 |
0.95 |
0.17 |
0.00 |
|
SD = 0.25 |
1.20 |
0.81 |
0.40 |
0.13 |
|
SD = 0.5 |
1.11 |
0.84 |
0.57 |
0.36 |
|
SD = 1 |
1.19 |
0.99 |
0.82 |
0.65 |
|
NOTE: See text for specification of scenario. |
||||
In this simulation, as in the others, for each value of truth and standard error, a large number of values (20,000) are drawn from the corresponding normal distribution. The allocation is calculated under the THRESH rule, and then the allocations are averaged. Because each year is independent in this simulation, it suffices to simulate a single year.
Note that with exact information (no sampling variance), each domain receives its proportional allocation if above the threshold, and nothing if below, as required by the funding formula. However, with increasing sampling variance, the below-threshold domains have increasing probabilities of estimates above the threshold and therefore an increasing expected benefit. This effect, of course, kicks in more quickly in domains for which the true rate is just below the threshold, as shown by comparing the last two columns of Table A-1. The situation for above-threshold domains is more complex. With modest amounts of sampling variability, the probability that the sample estimate falls below the threshold, causing the domain to lose all of its funding for the year, becomes large enough to reduce the domain's expected benefit. When sampling variability becomes sufficiently (perhaps unrealistically) large, however, the expected payoff begins to increase again, because the positive errors (which are in theory unbounded) begin to compensate for the negative errors (which are bounded because the payoff is never negative). This increase in expectation is accompanied by a drastic increase in variance, as eligibility for any funding approaches a coin toss (assuming, again unrealistically, that the sampling distribution is symmetrical).
Reading down any column of Table A-1, one can see how changing sampling variance affects the expected payoff to a domain at each value of the “truth.” Particularly for true rates close to the threshold, the differences down the column can be large. It is difficult to imagine a rationale for giving an area a larger expected payoff because a decision was made about sample design for a survey that caused that area's rate to be estimated less precisely.
As sampling error increases, the sharp cutoff envisioned in the formula is replaced with an increasingly smooth (ultimately almost linear) relationship between population rate and expected payoff. It is arguable that sharp thresholds in funding formulas are not entirely sensible and that a smoother transition would give more stability and less importance to very small shifts near the threshold. However, smoothing expected payoff around the threshold through sampling noise is a poor way to do this. For areas with substantial sampling variability, the threshold magnifies annual variability in allocations relative to a smooth transition, even though the expected allocation over time is smoothed. Furthermore, the amount of smoothing around the transition is dependent on the design
for each area, and the cutoff at the transition is sharpest for areas with small sampling variability.
Scenario 2: Effects of Sampling Variability with a Hold-Harmless Provision
Figure A-1 shows the effect of sampling variability when there is a hold-harmless provision at 80 percent and the underlying standardized population poverty rate is constant at 1 (HH, CONS). Each panel pertains to a different estimator (SINGLE, MA3, MAE3). The solid line in each panel shows the “correct” allocation (based on the true value 1), and the dotted lines show the expected allocations with annual SD = 0.1 (triangle), 0.25 (+), and 0.5 (X). In this simulation, we draw the estimated rates independently in each year (simulating independent sampling). Nonetheless, the calculated allocation is affected, through the hold-harmless provision, by the allocation in the previous year.
Expected allocations in the first year are all equal to 1 because we assume no effect of hold harmless in the first year. In successive years the expectation climbs because the allocation is “ratcheted up”—that is, when it is increased by sampling variability in one year, it cannot decrease very much in the following year. Comparing the three panels, we find that use of a moving-average estimator of the rate greatly mitigates this effect, more than would be expected simply due to the reduction in variance. With a 3-year moving average, the standard deviation of the estimates for the scenario with annual SD = 0.5 is reduced to 0.5/√3 = .289, but the bias in year 4 is reduced to .029 (estimated by simulation), much less than the bias of .057 that is found with single-year estimates with SD = 0.25. This reduction in bias is a consequence of the fact that the 3-year moving-average estimates for consecutive years use data from two of the same years (and one different year at each end), so the series of estimates is positively autocorrelated (i.e., a year with a positive estimation error will tend to be followed by another year with a positive error). Hence, the moving-average estimates are smoother over time than independent annual estimates with the same standard deviation, and big jumps in estimates that trigger the hold-harmless provision are less likely to occur. (See Scenario (5) below for an analysis of this greater smoothness.) This result illustrates that a linear smoothing procedure can give some of the stability that is sought with a hold-harmless provision, without the size-related bias that hold harmless can engender.
The combined effect of a hold harmless and a threshold is even more drastic than the effect of either alone. Table A-2 is comparable to Table A-1 above for the effects of a threshold, but it assumes that there is an 80 percent hold-harmless provision as well. (The results shown are for year 4, when the effects of hold harmless have approached—steady state.) The results are extremely sensitive to sampling variances.—Domains for which the actual standardized poverty rate is just below—the threshold (set at 1), but that have a large measurement standard—deviation, have very high expected allocations relative to what they—would have received if there were no measurement error. This result—occurs because once a domain goes above the threshold and receives—funding, it takes a long time for it to drift down toward zero funding—even if its estimates are below the threshold for the following several—years.
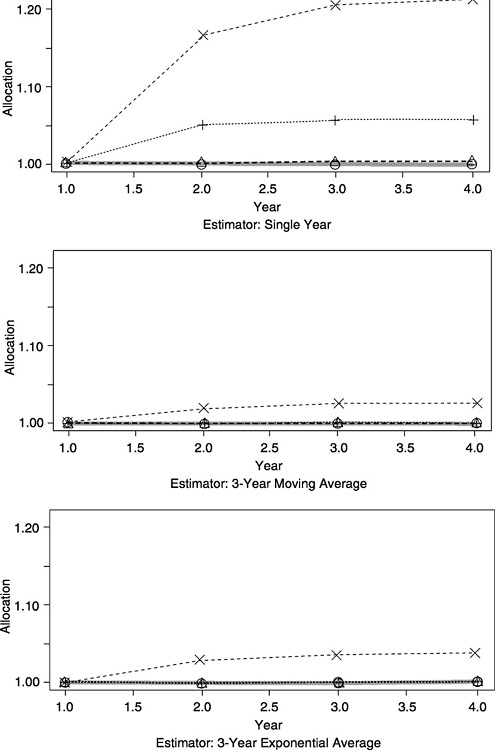
FIGURE A-1 Effects of sampling variability with a constant poverty rate and hold-harmless provision: Correct allocations and three estimation methods.
NOTE: Results for scenario (2); see text for details.
TABLE A-2 Results for Scenario (2) (Modified): Effects of Sampling Variability with a Threshold and an 80 Percent Hold-Harmless Provision; Single-Year Estimator
4, when the effects of hold harmless have approached steady state.) The results are extremely sensitive to sampling variances. Domains for which the actual standardized poverty rate is just below the threshold (set at 1), but that have a large measurement standard deviation, have very high expected allocations relative to what they would have received if there were no measurement error. This result occurs because once a domain goes above the threshold and receives funding, it takes a long time for it to drift down toward zero funding even if its estimates are below the threshold for the following several years.
Scenario 3: Effects of Various Linear Estimation Methods with a Trend
Figure A-2 shows a hypothetical downward trend (solid line) in standardized population poverty rates, assumed to start in year 2 after a period of constant rates, and the expected allocations with three estimation methods: single-year data (SINGLE = triangles), 3-year moving average (MA3 = +), and exponentially weighted MA (MAE3 = X). Sampling standard deviation is not relevant to the calculation of expected allocations in this case: the estimators and formulas are linear, so that adding variability does not affect the expectation of the estimators. As expected, the single-year estimates track (in expectation) the correct allocations, but the moving averages trail them. The exponentially weighted average, because it weights more recent years more heavily, trails slightly less far behind. This result illustrates the bias-variance tradeoff inherent in modeling. Note that as long as “what goes up must come down,” the upward bias during a decline is balanced by a downward bias during an increase.
The optimal weighting method (number of years and weights on each lag) depends on sampling variances, the magnitude and pattern of process variability over time, and the importance attached to timeliness and accuracy of estimates.
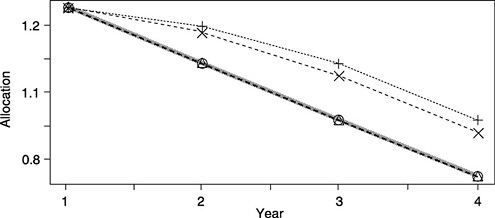
FIGURE A-2 Effects of a downward trend with no hold-harmless provision: Correct allocations and three estimation methods. NOTE: Results for scenario (3); see text for details.
Scenario 4: Effects of Trends with a Hold-Harmless Provision
Figure A-3 shows a scenario similar to that in scenario (3) but with a hold-harmless provision. The sampling standard deviation is now relevant, and the three values of the standard deviation are labeled as in scenario (2). The effects are a combination of those seen in (2) and (3): moving averages lag behind the trend, and domains with large standard deviations tend to be “ratcheted” upwards.
Figure A-4 shows the same scenarios except with an upward trend in rates. Here, the bias due to hold harmless has been mitigated: with increasing rates, the hold-harmless provision is less likely to have an effect.
Scenario 5: Comparison of Hold Harmless and Moving Average as Methods for Moderating Downward Jumps
In this set of three scenarios, estimates fluctuate around a mean of 1 with SD = 0.5. These fluctuations represent the sum of sampling error and uncorrelated year-to-year variability in the population rate. We compare three approaches to reducing the magnitude of downward jumps from year to year. In the first, an 80 percent hold-harmless provision is applied to annual data with SD = 0.5 (HH). The second is like the first except that we assume that the standard deviation is reduced to SD = 0.5/√3 (HH3). (If variability is entirely due to sampling error, this reduction in the standard deviation could be obtained by multiplying sample size by 3.) The third scenario assumes that a formula without a hold-harmless provision is applied to a 3-year moving average (MA3, no HH) and SD = 0.5/√3, the same as that for the second scenario. For evaluation, we look at the changes in allocation from year 3 to year 4, when the hold harmless has almost reached steady state. We calculate the fraction of changes that go in the downward direction, the mean of those changes, and the mean of the changes in the upwards direction; see Table A-3.

FIGURE A-3 Effects of a downward trend with a hold-harmless provision: Correct allocations and three methods. NOTE: Results for scenario (4); see text for details.
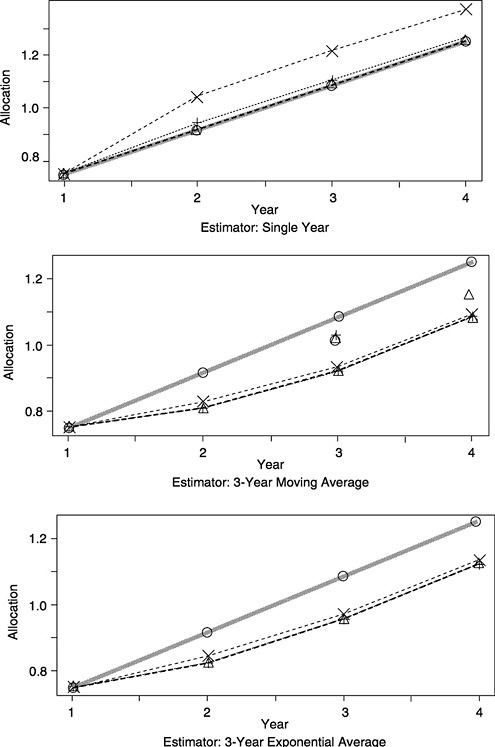
FIGURE A-4 Effects of an upward trend with a hold-harmless provision: Correct allocations and three methods. NOTE: Results for scenario (4); see text for details.
TABLE A-3 Results for Scenario (5): Hold Harmless and Moving Average as Methods for Moderating Downward Jumps in Allocations
As expected, the moving average is equally likely to go up or down in the absence of hold harmless. The asymmetry of the hold harmless leads to more downward than upward shifts: because the downward shifts are limited in magnitude, there must be more of them. Another way of explaining this effect is that the upward bias of the hold harmless with a large standard deviation means that the current allocation tends to be higher than the long-run mean rate and will take more downward than upward steps.
Comparing the mean magnitude of the steps, we find that in the realistic comparison of the first and third columns of Table A-3, both the downward and upward steps engendered by the hold-harmless provision are larger on the average than those engendered by a moving-average estimator with a proportional formula. Even the second column (representing a somewhat unrealistic scenario, since it assumes that an expansion of sample size could be afforded) has downward changes no smaller than those obtained with a moving average. This result suggests that use of a moving average can be as effective as a hold-harmless provi-
sion in moderating downward swings in allocations. The cost of using a moving average, however, is that it is less responsive than a single-year estimate to upward jumps in the rate; such sensitivity might be valued if one of the purposes of the allocation formula is to be responsive to rapidly rising needs.
EFFECTS OF A FIXED GLOBAL BUDGET FOR ALLOCATIONS
The preceding simulations have been based on the assumption that each area's fund allocation is independent of those received by all other areas. Often, this assumption is unrealistic. A common situation is that in which there is a fixed global budget for a program, so that the funding of each domain is dependent on the “demand” for funding of each of the other domains. On the surface, this appears to be the case for programs such as the Title I education program. We must note, however, that the assumption of a fixed global budget may also be an oversimplification, since Congress may respond to an increased demand for funds—due to increasing poverty rates—by increasing the total amount available for distribution. Congress may also increase the total amount when reallocation of a fixed global budget would reduce funds to some areas by more than it can collectively tolerate, even if poverty rates have not increased on average. For the analysis in this section, nonetheless, we assume a fixed global budget.
In addressing the effects of the interactions among allocations to different areas, it is critical to note that they are mediated through some parameters of the fund allocation formula. For example, suppose that a globally budgeted amount is distributed among domains in proportion to the number of individuals who fall under a criterion of need. If the population eligible for aid is overestimated in some area (holding estimates for other areas constant), the amount distributed per eligible person (the key parameter of this funding formula) would be driven down, which would affect the allocations for other areas. In general, if the number of areas is large, the aggregated magnitude of the effects on allocations due to applying a nonlinear formula with imprecise data may be close to its expectation, simply because it is the average of contributions from a large number of areas. Hence, it may be highly predictable from mathematical calculations or simulations of bias, such as those illustrated in the previous section. The total effect of sampling error may then be calculated by estimating the effect of these biases on the formula parameter and, consequently, the expected effect on the estimate for the single area of interest.
We now restate this argument using a more formal notation. Let f(xi,θ) be the formula allocation for domain i, which has a measurable
characteristic xi related to need if the overall formula parameter is θ. The parameter θ may be something that is calculated in the process of applying a formula in which θ is not specified: for example, if a fixed budget is distributed over a variable pool of recipients, the amount per recipient depends on the number of recipients. For simplicity of presentation, we assume that f is nondecreasing in both xi and θ: that is, needier areas receive more than they would if they were less needy, and increasing the formula parameter increases (or leaves constant) the amount allocated to each area. Simple illustrations include the following:
-
f(xi,θ) = xiθ, simple proportional allocation, where xi is the number in need in the area. In this formula, θ is simply the amount allocated per needy person.
-
f(xi,θ) = wih(xi)θ, where wi is a measure of size (e.g., total population), and h(xi) is a possibly nonlinear function of a rate (e.g., h(xi) = 0 for xi < c, h(xi) = xi otherwise, representing a rate threshold for receiving an allocation). We regard wi as a fixed quantity, which does not need to be included in the formula explicitly. Example (i) is a special case of this class of formulas.
-
f(xi,θ) = awixi for xi > −θ, 0 otherwise, with a a predetermined constant. Suppose again that xi represents a rate. Then under this formula, the neediest areas, defined as those exceeding a certain threshold rate of need −θ, receive a predetermined allocation a per needy person, while those below the threshold receive nothing. (Note that we use −θ to maintain the condition that f is increasing in θ.) Here, there is a “floating threshold” in the sense that the threshold (rate) for receiving benefits is determined by the level at which the budget is exhausted.
If xi is estimated from a sample, the allocation to domain i is f(xi +εi,θ), where εi is measurement (sampling) error. The statistical sampling distribution of εi depends on xi and some sampling characteristic or characteristics si, which one might think of as the sampling standard error of the estimate and perhaps some more complex properties of the error distribution. Finally, suppose that the expected allocation for an area, taking the expectation over the distribution of εi given si, is fs(xi,si,θ). Note that this is essentially the quantity that was studied through the simulations of the preceding section; in particular, we were concerned about the sensitivity of fs(xi, si,θ) to si.
Given a fixed budget A, the value of θ used in the allocation is determined by the relationship ∑if(xi + θi,θ) = A. If the number of areas is fairly large, we may approximate the sum by its expectation, ∑ifs(xi,si,θ) = A. Hence, the expected allocation to domain i, fs(xi, si,θ), is affected by the
sampling properties for the measurement in that domain and by the effect of sampling properties averaged over other domains.
It is difficult to draw any fully general conclusions about the effect of sampling error on allocations to each area. It is possible to draw fairly general conclusions, however, for allocation formulas of the forms (i) and (ii) above, where θ appears as a proportionality constant in the formula. In that case, the ratio of allocations for any two areas is free of θ; furthermore, the ratio of the ratio of expectations to the ratio of correct allocations is also free of wi. The latter ratio (for comparison of two domains labelled i, j) is given by

where hs is defined analogously to fs. The proportional bias

and the way it is affected by sampling properties si, is precisely what the previous simulations studied. Hence, we conclude that for a large class of formulas, the results we have obtained for single areas apply straightforwardly to comparisons of the relative effect of sampling error in different areas. We anticipate that in many situations that do not quite fit the structure of (ii), fairly similar results would nonetheless apply: that is, areas for which the sampling properties of their estimates augment their expected allocations the most with fixed values of θ are also advantaged when they must share a global budget with other areas.
CONCLUSIONS
From a legalistic and formal standpoint, modification of the estimation procedure and modification of the formula are two entirely different enterprises. There are good reasons from the standpoint of the division of labor among the agencies of government to maintain this distinction. In fact, though, the formula, estimation procedure, and data sources are parts of a coherent whole. As pointed out in an example above, the distinction between the estimation procedure and the formula is often entirely arbitrary, an expression of the same calculation with different labels. Given this fact, it would be shortsighted to give attention to esti-
mation and data collection while ignoring formulas. The goal cannot be simply to devise an estimation procedure that replicates allocations that were obtained with outmoded data sources. First, new data may be superior to old data, so that the old system can only be replicated by throwing away valuable information. Second, procedures used with older sources may reflect only the limitations of those data, not an intention to obtain a specific outcome.
As the illustrations suggest, interactions among sampling properties of the data, estimation methods, and funding formulas may produce unanticipated and sometimes undesirable effects. The long-term effects of linear estimators and formulas are fairly predictable. Results of some nonlinear methods, however, may be greatly affected, even on the average and in the long run, by sampling variances. This effect is problematical, because it almost inevitably leads to situations in which larger or smaller units tend systematically to get more than their proportional shares, other factors (poverty rates) being constant. Furthermore, decisions about sample allocation should be made on technical grounds related to optimizing the overall accuracy of the survey, but these decisions have implications for outcomes for specific areas when the outcomes are sensitive to variances. Such a link between methodological choices and outcomes puts the data collection and estimation agencies of government in an untenable position.
Widely used nonlinear allocation procedures include hold-harmless provisions and thresholds. These could be replaced to some extent by estimation and allocation procedures that accomplish some of the same goals but have less paradoxical properties, so their use should be reconsidered. Yet some nonlinear and indirect procedures, such as empirical Bayes estimation, can be shown to produce estimates with improved accuracy relative to direct estimators. Therefore, they are likely to be useful when high-precision direct estimators are not available. Indirect estimators tend to have sampling characteristics (such as variation from year to year) that are less dependent on sample size than those of direct estimators, but they may be affected by model biases that tend to persist over time. Their interaction with allocation procedures needs to be better understood as they become more widely used.
Funding formulas are often ingenious “ad hockeries,” hammered out from a political process based on compromise. Although notions of equitable and efficient allocation of resources are implicit in them, they do not, by themselves, define those notions. It is the responsibility of those who generate data and implement formulas, and best understand how they work together in practice, to consider the ways that new procedures and data change a formula's effects and to suggest revisions to formulas that best serve their original objectives.
























