Improbable Is Not Impossible: Decision Making Under Uncertainty
LINDA K. NOZICK
School of Civil and Environmental Engineering
Cornell University
Ithaca, New York
INTRODUCTION
Risk is the result of chance and negative outcome. An earthquake strikes. A bomb planted by a terrorist explodes on a crowded street. A recession hits. Risk is inherent in every aspect of our lives. Personal decisions, such as which job to take or which investments to make, involve risk, as do decisions by corporations and governments. Consider, for example, residential building codes, which are developed and enforced by governments to promote health and safety. In general, code changes that improve safety add to the cost of construction. What level of safety should be mandated? If building codes are strengthened significantly, the costs of construction could make new homes less affordable. More expensive homes draw money that otherwise might be spent on other goods and services. High costs could make it more difficult for people to purchase new homes thereby causing them to remain in older homes that may have been built to lower standards (Hammitt et al., 1999).
Risk analysis and decision making under uncertainty are inherently cross disciplinary. Risk is primarily concerned with measuring the probability and severity of potentially negative outcomes. Risk is a scientific concept that can be qualitative or quantitative or both. By contrast, decision making, which is about the acceptability of risk, has political, ethical, and personal dimensions (Lowrance, 1976). Some will argue that risk is primarily subjective, that the notion of risk is a response to the human need to cope with uncertainty and that we develop models whose structures and uses are riddled with subjective judgments (Slovic, 1999). We must acknowledge that all models have an element of subjectivity; but the key difference between the “scientific” and “subjective” views of risk is the extent of this subjectivity. For the purposes of this paper, I
will focus on risk analysis as a scientific enterprise and simply acknowledge that the alternate view exists and has some merits worth discussing.
The focus of this paper is on making decisions when there are multiple objectives and significant uncertainties associated with the possible outcomes. I will illustrate these ideas with a case study of hazardous materials transportation.
MEASURING RISK AND COMPARING ALTERNATIVES
The most common measure for estimating risk is expected value. Expected value is defined as the sum of the multiplication of each potential consequence by its probability of occurrence. This measure has advantages and disadvantages. The advantages include: (1) it is easy to understand, and (2) the risk of an action or alternative can be summarized in a single value. The disadvantage is that it gives equal weight to high-probability, mild-consequence outcomes and low-probability, high-consequence outcomes. For example, in an expected value calculation, an earthquake that destroys a collection of homes, which has a low probability of happening but catastrophic consequences, is treated the same as damage to the exterior of homes that has a high probability of occurring but minor consequences. Clearly, this is a distortion of the true impacts. To overcome this limitation, descriptions of the probability distribution of consequences are often used. These descriptions can be conditional, if the consequences are in a given portion of the distribution, such as the upper quartile; or unconditional, if they are applied to the entire distribution.
Choosing between alternatives, each of which can have a number of different consequences, is often a difficult task. The task is considerably simpler if the cumulative distribution function (CDF) of consequences for one alternative, F(x), is equal to that of another alternative, G(x), for some consequences and is larger for others. That is, if F(x) ≥ G(x) ∀x, F stochastically dominates G. Notice that in Figure 1a the probability that any outcome is x or less is greater for F(x) than for G(x). Unfortunately, this is seldom the case. Usually the CDFs cross. If they cross at a level of consequence that is sufficiently rare, we might still be willing to say that F stochastically dominates G or, equivalently, that F partially stochastically dominates G. Consider the example in Figure 1b. Only very rare negative events are slightly more probable under alternative F.
MULTIPLE OBJECTIVES
Making trade-offs between conflicting, noncommensurate objectives is at the core of decision making. Uncertainty simply adds to the difficulty. For example, consider making decisions about aircraft safety. There is an inherent trade-off between the thoroughness of inspections of people and baggage and delays. The more carefully people and baggage are examined, the less likely a
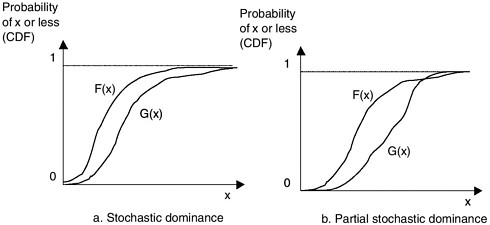
FIGURE 1 Stochastic dominance and partial stochastic dominance.
potentially dangerous item is to be smuggled aboard a plane. However, the more complete the inspections, the greater the delay.
The concept of an optimal choice when there are multiple objectives is significantly different than when there is a single objective. With a single objective, the performance of one alternative or one set of alternatives is optimal in terms of the objective. With multiple objectives, there can be many solutions, commonly referred to as a nondominated set, each of which represents different trade-offs. All of the solutions in this set are equally bad with respect to all objectives. The core question is finding an acceptable trade-off between achieving one objective and failing to achieve another, or partly achieving both to an acceptable degree. Typically, there are no “right” or “wrong” answers, and different individuals may make different decisions.
CASE STUDY: ROUTING HAZARDOUS MATERIALS
More than 800,000 hazardous material (hazmat) shipments occur daily in the United States, and the total volume of hazmat shipped annually is about 3.9 billion tons. The U.S. Department of Commerce estimates that approximately one truck in five on U.S. highways is carrying hazmat. Even though the safety record of hazmat transportation is very good, significant public concerns have been raised about the risks to people and the environment from hazmat shipments.
This case study concerns the application of an algorithm for routing a hazmat shipment when there are multiple objectives and the performance of each facility with respect to each of the objectives is stochastic and varies over time. Consider the possible consequences of an accident and the necessity of minimizing travel
time for a truck carrying a shipment of flammable liquid from Wilmington, Delaware, to Portland, Maine. The major hazard is assumed to be fire and/or vapor explosion in the event of an accident. Thus, the major at-risk population is other travelers on the highway near the shipment, rather than people residing some distance from the road. As a measure of consequence, we have used vehicle-minutes of exposure within x distance of the truck multiplied by the accident rate. That is, as the truck moves along the road, the vehicles potentially exposed to the risk of fire and/or explosion are (1) vehicles traveling in the same direction as the truck and less than x distance behind the truck and (2) vehicles traveling in the opposite direction at a distance of x or less ahead of the truck. In this case, x is assumed to be 0.5 miles. We then multiply 0.5 by the probability of an accident to calculate consequence.
An essential element of finding multiobjective shortest paths in stochastic dynamic networks is having a means of constructing the probability distribution of an attribute along a path. Because the probability distributions of the arc attributes are assumed to vary with time, a core step in the process is constructing a probability distribution of travel time from the point of origin to each node along a potential path. Because this is similar to adding together random variables, after a few links, the travel time distribution will be approximately normally distributed, so a procedure based on propagating means and variances can be expected to work well. Figure 2 illustrates a network with four links and estimated probability distributions for the time of arrival at each node. Notice that even with only four links, the arrival time at node four looks almost normally distributed. Therefore, all that is necessary is a procedure for propagating the mean and variance of arrival time at successive nodes.

FIGURE 2 Example of calculating travel time along a path.
Consider a path p from an origin node s to a destination node v in a stochastic dynamic network that includes a link connecting node i to node j. Let the random variable Yi denote the arrival time at node i (which is also the departure time from node i, because of the assumption of no waiting); let the random variable dij(Yi) be the travel time on link (i, j). It is clear that Yj = Yi + dij(Yi); and the conditional mean and variance of link (i, j) travel time are denoted by µ(yi) and v(yi). The mean and variance of Yj are given by:
E[Yj] = E[Yi] + E[µ(Yi)] (1)
Var[Yj] = Var[Yi] + E[v(Yi)] + Var[µ(Yi)] + 2 E[Yi µ(Yi)] – 2 E[Yi]E[µ(Yi)] (2)
Equations (1) and (2) allow propagation of the mean and variance of the arrival time at a node along the links of a path. Because traffic data are generally collected and summarized over discrete intervals (e.g., average speed over 1-hour intervals, or for a peak period of 3 to 4 hours), the data to support estimates of µ(Yi) and v(Yi) as continuous functions of time are generally not available. Therefore, in the analysis here, the estimates of E[Yi] and Var[Yi] are propagated using discrete intervals. These calculations are embedded in a label-correcting algorithm along with the concept of partial stochastic dominance discussed above. This allows us to efficiently search for “good” paths. For more information on the algorithm, see Chang et al. (2001a, 2001b).
A key decision in this case is determining the best path through the New York City area. One option is to pass through the city. That is, to stay on I-95 from Wilmington, Delaware, cross the George Washington Bridge, and take the Cross Bronx to the New England Thruway. Another alternative is to go around the city by taking I-287 across the Tappan Zee Bridge to the Cross Westchester Expressway to the New England Thruway. Figure 3 illustrates these choices.
Figure 4 illustrates differences in the distributions for the travel time and consequences for these two choices. Path A, which goes through the city, is shorter on average but more variable. In addition, the consequences on Path A are more severe than on Path B.
CONCLUSIONS
This paper illustrates the critical role of decision making under uncertainty in all aspects of our lives. There are at least two major challenges in this field. The first is improving the scientific enterprise of decision making under uncertainty, by improving methods of estimating probability distributions and methods of optimizing actions considering these distributions. The second challenge is to resolve the philosophical debate raging in the risk-based decision-making community. In this paper, I have focused on risk as the result of chance and negative outcome based on the underlying assumption that outcomes are pro-
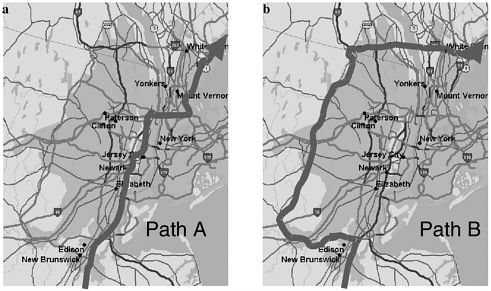
FIGURE 3 Two paths through the New York City area.
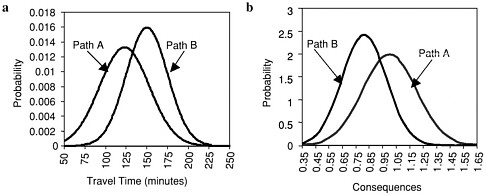
FIGURE 4 Travel times and consequences for Path A and Path B.
duced in ways that can be objectively analyzed. As evidence of subjectivity, those who argue that risk is inherently subjective often point out the great disparities in expenditures by different government agencies to save lives. For example, EPA spends about $7.6 million per year of life saved, whereas NHTSA spends about $78,000 per year of life saved (Tengs et al., 1995). Another example is the extremely difficult and complex decision required to address the
storage of spent fuel or high-level radioactive waste, which has been pending for many years (North, 1999).
ACKNOWLEDGMENTS
This work has benefited from the contributions of Drs. Mark Turnquist and Tsung-sheng Chang. The support of the National Science Foundation is gratefully acknowledged.
REFERENCES
Chang, T., L. Nozick, and M. Turnquist. 2001a. Routing hazardous materials with stochastic dynamic facility attributes. Working paper, Cornell University.
Chang, T., L. Nozick, and M. Turnquist. 2001b. Routing hazardous materials with stochastic dynamic facility attributes: A case study. Working paper, Cornell University.
Hammitt, J., E. S. Belsky, J. I. Levy, and J. D. Graham. 1999. Residential building codes, affordability, and health protection: A risk-trade-off approach. Risk Analysis 9(6):1037–1059.
Lowrance, L. 1976. Of Acceptable Risk. Los Altos, Calif.: William Kaufman.
North, D. W. 1999. A perspective on nuclear waste. Risk Analysis 19(4):751–758.
Slovic, P. 1999. Trust, emotion, sex, politics, and science: Surveying the risk-assessment battlefield. Risk Analysis 19(4):689–701.
Tengs, T. O., M. E. Adams, J. S. Pliskin, D. G. Safran, J. E. Siegel, M. Weinstein, and J. D. Graham. 1995. Five hundred life-saving interventions and their cost-effectiveness. Risk Analysis 15(3):369–390.







