4
Inference About Causal Discoveries Driven by Large Observational Data
The second session focused on inference about causal discoveries from large observational data such as electronic health records (EHRs). A primary goal of biomedical research with big data is to infer causative factors such as specific exposures or treatments; however, theories of causal inference in observational data (e.g., Pearl, 2000) remain relatively open in the context of large, complex data sets containing many treatment variables with possible interactions. Comparative effectiveness research using EHRs faces challenges related to potentially large amounts of missing data (“missingness”) and associated bias, confounding bias, and co-variate selection. Joseph Hogan (Brown University) discussed mathematical and statistical modeling of human immunodeficiency virus (HIV) care using EHRs. Elizabeth Stuart (Johns Hopkins University) further elaborated on synergies and trade-offs between mathematical and statistical modeling in the context of causal inference and public health decision making. Sebastien Haneuse (Harvard University) described a comparative effectiveness study on the effects of different antidepressants on weight gain using EHRs. In the last presentation, Dylan Small (University of Pennsylvania) demonstrated isolation of natural experiments within EHRs through a case study evaluating the effect of childbearing on workforce participation.
USING ELECTRONIC HEALTH RECORDS DATA FOR CAUSAL INFERENCES ABOUT THE HUMAN IMMUNODEFICIENCY VIRUS CARE CASCADE
Joseph Hogan, Brown University
Joseph Hogan discussed the use of EHRs to compare recommendations for when to initiate HIV care for patients in low- and middle-income countries. Although the work is still ongoing, this type of analysis can be used to infer how different treatment strategies impact patient progression through the HIV “care cascade.” He explained that the HIV care cascade is a conceptual model for understanding progression through stages of HIV care and is composed of (1) diagnosis, (2) linkage to care, (3) engagement or retention in care, (4) prescription of antiretroviral therapy (ART), and (5) viral suppression. Recommendations for when patients who test positive for HIV should begin treatment have evolved over time, said Hogan, in part due to the lack of available ARTs. In 2003, the World Health Organization recommendation was to begin ART if a patient’s cluster of differentiation 4 (CD4)—an aggregate measure of immune system health—fell below 200 cells/microliter, and this threshold has continually been increased due to accumulating evidence. The most recent guidelines call for initiating treatment for all HIV-infected individuals, regardless of CD4 count. The HIV care cascade is used to help formulate health care goals and institutional benchmarks—for example, the 90-90-90 goal put forth by the United Nations. This benchmark aspires to have, by 2020, 90 percent of HIV-infected patients aware of their status, 90 percent of those diagnosed with HIV receiving ART, and 90 percent of those receiving therapy having viral suppression, explained Hogan. These benchmarks present concrete objectives and create an impetus for empirical evaluation that must take into account statistical uncertainty, said Hogan. Evaluating progress in reaching these benchmarks is challenging because the necessary data are complex and come from multiple sources, and the care cascade is a dynamic and complex process. Furthermore, there is a trade-off between rigor and clarity, said Hogan, as program managers need interpretable information to evaluate progress and make decisions about new policies or interventions.
One of the simplest approaches is to aggregate data into a histogram showing the number of patients in each stage, which presents a static snapshot and provides limited insight into the cascade as a process. More recently there is growing interest in modeling the entire HIV care cascade, typically using microsimulation techniques based on complex, nonlinear state-space mathematical models. Typically these approaches assume an underlying parametric model, aggregate data from numerous different sources to quantify relevant parameters, calibrate the model against known target outcomes, and then explore the effects of alternative interventions through iterative simulation. Mathematical models are modes of
synthesis that are advantageous because they can represent highly complex systems, and calibration ties the model to some observed data, said Hogan. However, there are several limitations to keep in mind when interpreting results; for instance, it is unclear if the models represent one population of interest and reflect causal effects when parameter values are adjusted. Hogan provided an example from the literature of one such model used to compare the effects of different treatment strategies on patients’ progression through the care cascade (Ying et al., 2016; Genberg et al., 2016). The model specifies 25 states as a function of a viral load and CD4 count and defines a system of equations to calculate state transition probabilities based on primary data and the literature. With values for all parameters, the model is run and calibrated using 30 years of historical data, and then the model is used to project differences in HIV prevalence and incidence associated with alternative scenarios of treatment and home counseling. Nonetheless, Hogan said, without formal measures of uncertainty it is unclear whether the modeled differences in HIV incidence are significant.
With growing availability of EHRs containing longitudinal data for thousands of patients, Hogan explained that it is possible to develop statistical models of the HIV care cascade that are representative of a well-defined population in actual care settings. However, he cautioned that using observational EHR data can be challenging compared to using data from a cohort study due to irregular observation times and abundance of confounding factors. More fundamentally, it is difficult to operationalize concepts such as “being retained in care” from observational EHR data, said Hogan, and requires up-front effort somewhat analogous to preprocessing of genomics data.
Using data extracted from EHRs and maintained by the Academic Model Providing Access to Healthcare (AMPATH) consortium, Hogan described a statistical model for comparing the effects of two HIV treatment strategies—treat upon enrollment regardless of CD4 count or treat when CD4 ≤ 350cells/microliter—on patient progression through the care cascade. The database included information on over 57,000 individuals in care. A patient can be in one of five well-defined states: engaged, disengaged, lost to follow-up, transferred, or dead (Figure 4.1A). The probability of transitioning from one state to another is calculated from the aggregated AMPATH EHR data set. Based on these probabilities, the one-step transition model is used to predict the probability of state membership from enrollment through 1,800 days (Figure 4.1B), which stops short of causal inference but presents data in an easily interpretable format for health care decision makers.
Hogan extended this model to compare the two treatment strategies mentioned above by assuming that treatment is randomly allocated for individuals sharing the same observed-data history, that the length of follow-up depends only on the observed-data history, and that the model follows first-order Markov dependence. Thus, implementing this method requires fitting a sequence of observed-data
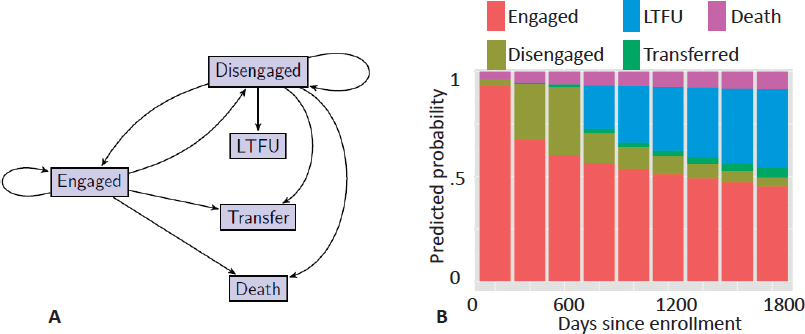
models for state membership conditional on previous CD4 count, treatment history, and other covariates, as opposed to the complex model assumed in mathematical models. The method also requires an observed-data model for time-varying covariates such as CD4 count, which can be checked for adequacy and elaborated if the fit is poor. Hogan illustrated how to implement the method for the case where time-varying CD4 count is treated as the main confounder. The method is implemented with a G computation algorithm using Monte Carlo simulation to average over the distribution of time-varying CD4 count (i.e., to calculate the high-dimensional integral over multiple time points). Hogan showed that the resulting predicted-state probabilities over time for the two treatment strategies that indicate starting treatment upon diagnosis and regardless of CD4 count leads to more patients remaining engaged and fewer patients lost to follow-up. Building a statistical model allows for formal quantification of uncertainty and application of standard methods, such as confidence intervals and hypothesis tests, to support inferences about effects of interest.
In comparing statistical and mathematical approaches to modeling the HIV care cascade, Hogan described the former as beginning with as much data as are available and building a simple mathematical model to describe the data, whereas mathematical models typically focus on building a more complex process model and then using select historical data for calibration. In short, mathematical models focus more on the model and less on the data, and conversely statistical models focus more on the data and less on the model. Given the abundance and complexity of information
in EHRs, there is an opportunity to combine elements of both approaches to make models that align closely with data but support a higher level of complexity, said Hogan. Mathematical modeling techniques can enrich statistical models in several ways—for example, in representing missing information in data sets or integrating outside data—with the goal of increasing model complexity while maintaining close alignment with observed data from a specific cohort. He suggested that statistical principles be integrated into informatics systems to ensure that decisions based on EHR data are well-grounded by rigorous inferences. Similarly, Hogan described the need for a framework for grading evidence that is used and produced by models—for example, by considering if the data describe a well-defined population of interest, if different sources of uncertainty are identified, if the model fit is evaluated, among other criteria. Hogan concluded that as complex, messy, information-rich EHR data become increasingly available and are potentially used to inform treatment decisions, practice patterns, and health care policy, “Statistical principles could hardly be more important.”
DISCUSSION OF CAUSAL INFERENCES ON THE HUMAN IMMUNODEFICIENCY VIRUS CARE CASCADE FROM ELECTRONIC HEALTH RECORDS DATA
Elizabeth Stuart, Johns Hopkins University
In mental health research there is increasing interest in comprehensive systems modeling, said Elizabeth Stuart, which is an area ripe for combining mathematical and statistical modeling. However, large-scale mathematical models typically require more assumptions than statistical models and may contain unnecessary complexity that is irrelevant to the specific decision context. There is a tension between creating large, detailed models that are descriptive of real-world complexities and small, simpler models that are often required to answer a given question. Thus it is critically important to target analyses toward particular parameters or questions of interest, said Stuart, as a way to simplify models and limit assumptions. For example, structural equation models are powerful for exploratory analyses because they include more effects and correlations than other inference techniques such as linear regression; however, these models require additional assumptions that may not be valid or necessary to answer questions related to a single causal effect (VanderWeele, 2012). When using methods that require strong assumptions and data without good empirical estimates, Stuart encouraged researchers not only to acknowledge and communicate the limitations, but also to assess the sensitivity of results to those limitations. It is critical to keep the ultimate goals and quantities of interest in mind when developing methods to evaluate evidence, she said.
Another challenge when estimating and drawing more complex models for causal inference is formalizing the potential outcomes. For example, in comparing the effectiveness of two treatment strategies there are two potential outcomes: a patient either receives treatment or stays in the control group. These are different random variables that are almost never both depicted on graphical models. Stuart said that it can be problematic to bundle the two outcomes together because it is possible that there is a different relationship between the covariates and outcome under one treatment than the other treatment. To demonstrate this point, Stuart described her experience analyzing the effectiveness of a marital intervention using the self-reported variable “relationship quality,” which was interpreted differently by subjects in the intervention (treatment) and control groups. For example, some subjects who did not receive the intervention and divorced still reported high relationship quality because they rarely had to interact with their partner, whereas other subjects conceived of “relationship quality” differently.
Regarding standards of evidence and the pros and cons of different study designs, Stuart described the ongoing debate in mental health research regarding experimental versus nonexperimental studies. Conventional wisdom is that experimental studies are always preferable because they allow greater control and lower bias, but this may be misleading when the objective of the study is to estimate a population treatment effect, said Stuart. It is critical to consider both internal and external validity as well as sources of bias (Imai et al., 2008), she said, and when estimating population effects it is possible that a small nonrepresentative randomized trial actually has more bias than a large nonexperimental study in a representative sample. Stuart was optimistic that with increasing access to big data such as population-wide EHRs, there would be the opportunity to conduct well-designed nonexperimental studies that provide better evidence about treatment effectiveness in the real world.
In conclusion, Stuart reiterated that the community needs tools to assess which parameters and assumptions matter most in large, complex models and to prioritize these for further investigation and refinement. One strategy is to formalize sensitivity analyses, particularly in large, complex mathematical models with many underlying assumptions and parameter values that are characterized by high or unknown uncertainty. In addition to uncertainty, there is a need for methods to account for the fact that data drawn from multiple studies represent different populations, said Stuart. Finally, it is relatively easy to perform validation exercises with predictions, but validation of causal inferences is more nuanced and requires further work.
PANEL DISCUSSION
During a panel discussion with Joseph Hogan and Elizabeth Stuart following their presentations, a participant mentioned a technique called Bayesian melding1 and inquired as to how much it informed Hogan’s work. Hogan responded that he is aware of this technique and similar work on Bayesian calibration that specifies full likelihood distributions for variables and then collects them into a common model. Moderator Michael Daniels (University of Texas, Austin) commented that although the methods may be similar, the application contexts are different in that EHRs provide much richer data. Hogan explained that one approach for the EHR context would be to build out from a statistical model—for example, the AMPATH data have limitations in that many patients are lost to follow-up and, despite some evidence from other sources that many of the patients have died, the EHR data have incomplete information on mortality. Researchers associated with AMPATH have done tracing studies to track down a subset of patients who are lost to follow-up and then incorporate that information back into the statistical model to generate new estimates of mortality across the population of interest. Going a step further, said Hogan, would be identifying data collected from other studies to integrate into the AMPATH study, but this would require a strategy to account for the different populations being represented.
Another participant inquired how confounding variables should be identified, mentioning ongoing work in data-driven identification of relevant confounders using large, messy medical claims data sets. Stuart answered that confounding variable selection should ideally be driven by scientific understanding and be independent of the data, and she emphasized the importance of a strong separation between research design and analysis. This is often difficult in an EHR scenario, particularly if the analysis is looking across large numbers of parameters and outcomes. Additionally, much of the data-driven confounder selection work has been done with data from single time points, and it is important to consider how this changes with time-varying confounders. Hogan commented that CD4 was chosen as a confounder because it is arguably the strongest measured predictor of treatment selection and outcome, as evidenced by both empirical and scientific understandings of ART’s role in HIV suppression. Regarding the broader question, empirical selection of confounders is another example where there is tension between statistical theory and practice, said Hogan, because in theory it is impossible to know whether a sufficient set of confounders has been selected. He said he is hesitant to apply data-driven approaches to confounder selection using data such as those from an EHR, in part because the data structure is so irregular, but perhaps more importantly because it might not be a representative sample from
___________________
1 Bayesian melding combines mathematical modeling with data (e.g., Poole and Raftery, 2000).
a population of interest. Hogan described a hypothetical example: suppose HIV treatment recommendations are based on the CD4 count being above a specified threshold, yet in practice treatment is not allocated strictly according to the policy. That is, many people with CD4 just over the threshold receive treatment while many just under the threshold do not. If patients in a sample are selected from among those whose CD4 is near the threshold, it is possible that CD4 will not be chosen as a potential confounder based on purely empirical grounds because, in this subset, it will not be strongly correlated with receiving treatment. In this case, a person with contextual knowledge would recognize that this sample may not be well suited to addressing the causal question because it does not allow leveraging of important information from a well-known confounder. This limitation cannot be discovered by a confounder selection method that is purely empirical. The fundamental inferential issue in this hypothetical example is not the method used to select confounders, but rather whether analysts have a properly selected sample.
In the final question, a participant commented that mathematical models and microsimulation typically have some calibration against observed data taken to be ground truth and asked what was analogous when using statistical models for causal inference. Stuart responded that for any given individual, the causal effect cannot be known because one potential outcome might be observed while there is no information on the other. In practice, researchers can calibrate the control group and calibrate the treatment group, but there is a missing piece in bringing these together. Hogan agreed, saying that researchers should test sensitivity of findings to departures from key assumptions, particularly when drawing causal inferences from large observational data. Perhaps the most important of these is the assumption of “treatment ignorability” or “no unmeasured confounding.” Moreover, correctly predicting the outcome of a treatment from observed data does not validate that the treatment caused that outcome. He encouraged participants to think of causal inference in terms of factoring a joint distribution of observed and unobserved potential outcomes, and he noted that clearly separating these two components in a model makes untestable assumptions clear and leads to more coherent and transparent inferences.
A GENERAL FRAMEWORK FOR SELECTION BIAS DUE TO MISSING DATA IN ELECTRONIC HEALTH RECORDS-BASED RESEARCH
Sebastien Haneuse, Harvard University
Sebastien Haneuse began by reiterating a fundamental difference in the scientific goals of comparative effectiveness research—for example, Hogan’s presentation comparing two HIV treatment strategies—and exploratory analyses, as discussed in the workshop’s first session. With this context, Haneuse described a case
study using EHRs to evaluate whether different antidepressants or classes of antidepressants have differential impacts on patients’ long-term (i.e., after 24 months) weight change. Some drugs were hypothesized to lead to weight gain while others were not, and these side effects were assumed to be independent of effectiveness of the antidepressant. The analysis was a retrospective longitudinal study conducted with electronic databases maintained by the Group Health Cooperative, which contained full EHRs based on EpicCare as of 2005; pharmacy data dating back to 1977; and additional databases that track demographic data, enrollment information, claims data, and primary care visits. Inclusion-exclusion criteria were as follows: (1) the patient must be between 18 and 65 years of age, (2) the patient must have undergone a new treatment between January 2006 and December 2007, and (3) the patient must have been continuously enrolled for at least 9 months. Application of these criteria to the available EHR data resulted in a sample of roughly 9,700 patients from which data on weight, potential confounders, and auxiliary variables were extracted for the 2-year interval prior to initiation of the new treatment through 2009. Although weight is a continuous variable, EHR data contain only snapshots of a patient’s weight trajectory, said Haneuse, and there is wide variability among the frequency of visits across patients. Thus, some patients have rich information on weight change, while the majority of patients have limited information.
EHR data can provide a large sample size over a long time period at a low cost compared to dedicated clinical studies; however, it is critical to remember that EHR data were not collected to support specific research tasks. Haneuse encouraged researchers to compare available EHR data to the data that would result from a dedicated study, saying that observational data probably do not have comparable quality and scope. There are additional practical challenges to using EHR data, such as extracting text-based information contained in clinician notes, inaccurately recording information, linking patient records across databases, and confounding bias. Although some of these challenges are not new and are encountered in traditional observational studies, existing methods for addressing them are ill suited for the scale, complexity, and heterogeneity of EHR data, said Haneuse. There is an emerging literature focused on statistical methods for comparative effectiveness research with EHRs that has focused largely on resolving confounding bias, whereas problems of selection bias and missing data are underappreciated. In the context of the antidepressant study, EHR data would ideally contain information on weight at baseline and 24 months for each patient, yet in reality less than 25 percent of patients had both measurements, leaving 75 percent of patients with insufficient information to compute the primary outcome. One approach is to simply restrict the analysis to the subsample of patients for which complete data are available. However, this raises questions about the extent to which conclusions drawn from the subsample are generalizable to the population of interest. Haneuse defined selection bias as the difference between conclusions drawn from the subsample
and conclusions that would result from complete information for the entire study population. Selection bias can thus be framed as a missing data challenge, for which there is a large amount of literature and methods that may be useful.
The validity of all methods for missing data relies on the assumption that data are missing at random, which Haneuse explained means that missingness depends solely on known variables, and thus the analyst can control for missingness with known information. Evaluation of this assumption typically proceeds by conceiving of a potential mechanism that determines whether or not data are missing, identifying factors that influence this mechanism, and evaluating whether these factors are described in available covariates. Haneuse argued that focusing on a single mechanism is overly simplistic for EHRs, which are high dimensional and heterogeneous, and in the context of clinical health care provision. For example, in the case of antidepressant-related weight change, there is no single mechanism that is responsible for determining whether a patient’s weight is recorded, but rather a complex combination of patient and clinician decisions. This simplistic approach may not fully account for missingness and may result in residual selection bias, which can compromise the generalizability and utility of results, said Haneuse.
Haneuse described a general framework for addressing selection bias in analysis of EHR data. Given the high complexity and heterogeneity of EHR systems, it is unlikely that any single method will be universally applicable, so Haneuse suggested that researchers consider two guiding principles: (1) identify the data that would result from the ideal study designed to answer the primary scientific question and (2) establish the provenance of these data by considering what data are observed and why. This process will generally involve identifying all variables that would have been collected and indicating the timing of all measurements, with additional details depending on the goal of the study, before even looking at available EHR data. Conceiving of the ideal study and resulting data allows for a concrete definition of complete and missing data, which analysts can use to characterize why any given patient has complete or missing data. Specifically, Haneuse presented the general strategy of decomposing the single-mechanism model of why a patient has missing data into a series of more manageable submechanisms, with each submechanism representing a single decision. In the antidepressant-related weight gain case study, Hanuese proposed three sequential submechanisms that each partially determines if a patient’s EHR data contain a weight measurement at 24 months: the patient must be enrolled at 24 months, the patient must have been treated at 24 months (±1 month), and the patient’s weight must have been recorded at this treatment (Figure 4.2).
Breaking down missingness into more granular submechanisms allows each to be explored in greater detail, whereas the single-mechanism approach represents an average of these mechanisms. Haneuse evaluated the number of patients meeting the criteria of each submechanism, calling attention to the heterogeneity across
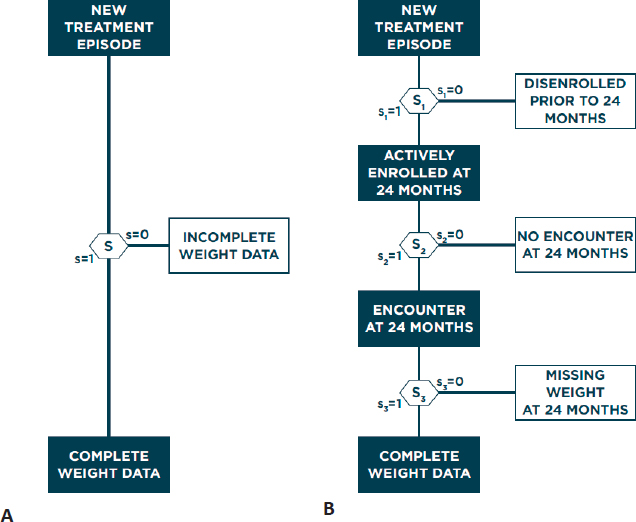
patient EHRs. Showing odds ratios from logistic regression models for the single-mechanism and three-mechanism models, Haneuse emphasized that different covariates can have different effects on each submechanism, which makes it difficult to interpret the significance of coefficients from the single-mechanism model. While the preceding example focused on three specific mechanisms, Haneuse said there are many alternative submechanisms that cause missing data that could be considered. For example, patients could receive treatment from an outside medical system or could receive clinical advice via the phone or secure messaging, both of which would result in missing weight measurements at 24 months. However, not all mechanisms will be relevant for any given EHR context or analysis question.
The proposed framework enhances transparency in assumptions regarding missing data, facilitates elicitation of factors relevant to each decision, and pro-
motes closer alignment between statistical methods and the complexity of the data, said Haneuse. Existing methods such as inverse probability weighting or multiple imputations can be combined with the multi-mechanism framework proposed, and multiple methods can be mixed in one analysis—for example, use of inverse probability weighting for some submechanisms and imputation for others—in what Haneuse termed “blended analyses.” Similarly, data-driven methods for variable selection developed to address bias from confounding may be adapted to the context of selection bias to understand which submechanisms and variables are most relevant. One of the most interesting areas, said Haneuse, is using this approach to prioritize future data collection efforts to supplement the information available in EHRs. He emphasized that these methods will become increasingly important as EHRs become the norm in clinical practice.
Haneuse concluded that EHR systems may be designed for secondary research purposes in the future but, until then, the majority of researchers using EHRs will try to model the best they can with the most information possible. Haneuse suggested that grounding the modeling within the context of the ideal designed study is appealing because it requires explicit definition of both the target population of interest and what it means to have complete data. This approach can help focus the scientific inquiry at the expense of unutilized information (for example, all of the patient weight measurements between 2 and 22 months), but this may be a relatively small price to pay, said Haneuse.
DISCUSSION OF COMPARATIVE EFFECTIVENESS RESEARCH USING ELECTRONIC HEALTH RECORDS
Dylan Small, University of Pennsylvania
Dylan Small reminded participants that using EHRs for comparative effectiveness research can be cheaper, faster, more representative of real-world effectiveness, and more statistically powerful (due to large sample sizes) than randomized trials. However, comparative effectiveness studies using EHRs face serious challenges regarding confounding and selection bias, said Small. He added that Haneuse presented an elegant framework for addressing selection bias that can better engage clinicians in thinking through why data are missing. Small remarked that another potential application of Haneuse’s multi-mechanism framework could be identification of subsets of the data for which missingness could be regarded as missing at random, analogous to selective ignorability for confounding bias (Joffe et al., 2010).
Shifting to confounding bias in EHR data, Small recounted calls to largely replace randomized trials with EHR-based studies (Begley, 2011), because EHRs contained detailed information on sufficient confounding variables to safeguard against errors that beguiled other observational studies in the past. However, Small
cautioned that confounding by indication—for example, that clinicians likely prescribe more aggressive treatments to patients with worse-perceived prognoses even if that treatment has a higher likelihood for side effects—will persist in comparative effectiveness studies using EHR data. He described Olli S. Miettinen’s warning that when a rational reason for an intervention exists, it tends to constitute a confounder (Miettinen, 1983); thus, the need for randomized trials is accentuated in studying a desired effect (e.g., comparative effectiveness research) more than when studying an unintended effect (e.g., comparative toxicity studies). Such confounding can be quite subtle and complex in the clinical health care context, and comparative effectiveness studies using EHR data need to critically consider why two patients with similar observed covariates received different treatments. Unless the treatments are assigned entirely at random, any causal inference made is subject to bias and is potentially misleading, said Small.
One strategy to develop reliable causal inferences from EHR data is to look for natural experiments contained in subsets of the data and apply quasi-experimental tools, such as multiple control groups or secondary outcomes known to be unaffected by the treatment, to test for hidden bias. Small described one example comparing the effect of childbearing on workforce participation (Angrist and Evans, 1998) to evaluate whether having more children reduces a mother’s working hours. He explained that answering this question presents challenges related to confounding by indication because many births are planned and nonrandom (Zubizarreta et al., 2014). One tool to isolate natural experiments from larger data sets is to focus on differential effects by comparing workforce participation between women who had twins versus single births, for example, as opposed to comparing women who have children to those with no children. “Risk set matching,” a second tool for isolating natural experiments, compares women who had similar covariates up to the time of birth—for example, comparing women who have had the same number of births (among other variables) as opposed to comparing mothers with three children to first-time mothers. Small showed results from the isolated natural experiment indicating that the median fraction of a 40-hour work week performed was slightly (approximately 8 percent) lower for mothers of twins compared to the control groups, and this difference became more pronounced with increasing numbers of births.
In a second example of comparing differential effects, Small described evaluation of the effects of pain relievers on Alzheimer’s risk, testing the theory that nonsteroidal anti-inflammatory drugs (NSAIDs) such as Advil™ may reduce patient risk. However, there is potential confounding from the possibility that early-stage Alzheimer’s patients are less aware of physical pain and thereby less likely to take NSAIDs. To control for this confounding, Small suggested comparing Alzheimer’s risk between patients taking NSAIDs and those taking non-NSAID pain relievers like Tylenol™ as one such natural experiment available in EHR data. Small concluded that EHRs and other sources of big data do hold a lot of promise, but long-
known problems of selection and confounding bias must be addressed. Isolating natural experiments is one strategy to reduce confounding bias.
PANEL DISCUSSION
In a follow-on panel discussion with Sebastien Haneuse and Dylan Small, a participant described Haneuse’s strategy of comparing EHR data to data that would result from the ideal randomized trial as the appropriate way for statisticians and other researchers to reason through causal discoveries made from big data, as opposed to simply extracting as much as possible using advanced methods such as machine learning. The participant asked if Haneuse had considered a way to quantify the extent of missingness, similar to a missing information ratio, relative to the ideal study design. Haneuse responded that the approach does allow for concrete definition of complete and missing data, though he had not thought about this particular issue of quantification.
Another participant asked generally what researchers in the field could do to raise awareness of these issues and make the appropriate statistical methods available, particularly given the anticipated growth in EHR data collection and availability. Haneuse said that it takes years before statistical methods from literature are adopted by practitioners, and he suggested that researchers engage in similar workshops and discussions more frequently. Another participant said that many issues and sensible approaches to using EHR data are known and documented in the literature, and Small commented that some journals are more statistically rigorous than others.
One participant said that conceiving of the ideal study design as a basis for defining data needs was potentially risky because it could lead one to disregard available data that do not correspond to this design—for example, not using patient weight measurements taken at 18 months. Haneuse clarified that those measurements do have useful information that should be used in solving the missing data challenge and reiterated that researchers should use the ideal study design to help define complete and missing data, using any information that is available.














