B
Nutrient Assessment of Individuals: Statistical Foundations
Chapter 3 provides an approach that can be used to answer the following question for nutrients with an Estimated Average Requirement (EAR), Can an individual's intake, observed for a small number of days, be used to determine if that individual's usual intake of a nutrient is adequate? Similarly, guidance on how to determine, for a given confidence level, whether an individual's usual intake exceeds the Adequate Intake (AI) or the Tolerable Upper Intake Level (UL) is also presented in Chapter 3. The statistical underpinnings and the implementation of the approaches provided are described in this appendix.
To begin, two important terms must be defined:
-
The observed intake of a nutrient by an individual on a given day is denoted bv Yj, where j denotes the day on which the intake Y was recorded. In this appendix, j = 1,...,n, is used to indicate that the number of daily intake observations for an individual can be any number (some arbitrary value n). In practice, n is typically less than seven, and is often no more than two or three. The observed mean intake for the individual over the n days is denoted by
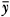 , and is computed as:
, and is computed as:
-
The usual intake of a nutrient by an individual is an unobservable long-run average intake of the nutrient denoted as y. Conceptually, the usual intake y could be computed as above if the number of
-
intake days (n) available for the individual was very large. In practice an individual 's usual intake is seldom known; instead, the individual's observed mean intake
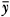 is used as an estimate of the individual's usual intake y.
is used as an estimate of the individual's usual intake y.
When assessing an individual's dietary intake, usual intake and not observed intake should be compared with the requirement to determine whether the intake is adequate (or whether it exceeds the UL).
Assessing the adequacy of an individual's intake of a nutrient by using only dietary information is difficult because neither the usual intake nor the actual requirement of the individual is known. The approach detailed here for assessing the adequacy of an individual's intake requires four types of information: the median requirement of the nutrient for the individual's life stage and gender group (the EAR), the variability in the requirement for the individual's life stage and gender group, the mean observed intake for the individual, and the day-to-day variability in intake of the nutrient for the individual. By combining this information appropriately, a method for estimating the adequacy of an individual 's usual intake of a nutrient can be derived. A similar approach may be used to compare observed intake to an AI or UL, and will be discussed later in this appendix.
USING THE EAR TO ASSESS ADEQUACY OF AN INDIVIDUAL'S OBSERVED INTAKE
Following are the assumptions for the statistical approach to evaluating the adequacy of an individual's observed intake:
-
The Estimated Average Requirement (EAR) is the best estimate of the individual's unobservable true requirement, denoted by ρ. The estimate for the individual's requirement is denoted by r, and r is set to be equal to the EAR of the appropriate life stage and gender group. The standard deviation of requirements in the population, denoted by SDr, is proportional to the uncertainty about how precisely r estimates ρ. If every individual had the exact same requirement for the nutrient, then r (which is set to be equal to the EAR) would be a precise estimate of each individual's requirement. Because individuals vary in their requirement for a nutrient, it is important to consider the extent of the variability in the group; the SDr is an indicator of how variable requirements are in the group.
-
The mean of n days of intake of the nutrient by the individual,
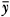 , is the best estimate for y, the individual's usual intake. The day-to-day variation in intake for a given individual, also referred to as the within-person standard deviation of daily intakes, SDwithin, is proportional to the uncertainty about the accuracy of
, is the best estimate for y, the individual's usual intake. The day-to-day variation in intake for a given individual, also referred to as the within-person standard deviation of daily intakes, SDwithin, is proportional to the uncertainty about the accuracy of 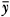 as an estimate of y. The mean (
as an estimate of y. The mean (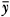 ) will be a reliable estimate of the usual intake y when the number of intake days n from which the mean was computed is large or when the SDwithin is low. If an individual eats the same diet day after day, then the day-to-day variability in intakes for that individual would be very low, and one or two days of intake information might be sufficient to precisely estimate that individual's usual intake of the nutrient. Conversely, a large number n of dietary intake observations is needed to estimate the usual intake of a nutrient for an individual whose diet is variable from one day to the next.
) will be a reliable estimate of the usual intake y when the number of intake days n from which the mean was computed is large or when the SDwithin is low. If an individual eats the same diet day after day, then the day-to-day variability in intakes for that individual would be very low, and one or two days of intake information might be sufficient to precisely estimate that individual's usual intake of the nutrient. Conversely, a large number n of dietary intake observations is needed to estimate the usual intake of a nutrient for an individual whose diet is variable from one day to the next.
It is implicitly assumed that food intake can be measured accurately in terms of quantity of food and food composition. Therefore, results from individual assessments should be interpreted with caution and where possible, should be combined with other interpretive data.
Thus the following statements can be made:
If y > ρ, then the individual's usual intake of the nutrient is adequate.
If y < ρ, then the individual's usual intake of the nutrient is inadequate.
Because neither y nor ρ is observed, ![]() and r must be used instead. Inferences about the adequacy of the individual 's diet can be made by looking at the observed difference (D), where
and r must be used instead. Inferences about the adequacy of the individual 's diet can be made by looking at the observed difference (D), where
D = ![]() − r.
− r.
Intuitively, if D is large and positive, it is likely that the true difference y − ρ is also large and that the individual's diet is adequate. Conversely, if D is a large negative number, then it is likely that ρ is larger than y and that the individual's intake is not adequate. The obvious question to be posed is, How large would D have to be before it can be concluded, with some degree of assurance, that the unobservable usual intake is larger than the unobservable requirement?
To interpret this difference between observed mean intake (![]() ) and the median requirement (EAR, the best estimate [r] of the unobservable ρ), one needs a measure of the variability of D. The standard deviation of requirements (SDr) and the standard deviation of intakes (SDwithin or SDi) can be used to estimate the SD of D, the difference between observed mean intake and r for the individual, as
) and the median requirement (EAR, the best estimate [r] of the unobservable ρ), one needs a measure of the variability of D. The standard deviation of requirements (SDr) and the standard deviation of intakes (SDwithin or SDi) can be used to estimate the SD of D, the difference between observed mean intake and r for the individual, as
Vr denotes the variance of the distribution of requirements in the group and Vwithin denotes the variance in day-to-day intakes of the nutrient. Both variances are computed as the square of the corresponding standard deviations. As the number (n) of days of intake available on the individual increases, the variance of the observed mean intake should decrease (i.e., the accuracy of the estimate for y increases). This is why Vwithin is divided by n when computing the standard deviation of the difference D.
The SDD increases as the
-
SDr increases,
-
SDi increases, or
-
number of intake days (n) available for the individual decreases.
That is, the more uncertainty that exists about the accuracy of the value D, the larger D will need to be before it can be confidently stated that the individual 's usual intake is adequate. The following extreme cases illustrate this approach:
-
If the intake of an individual could be observed for a very large (infinite) number of days, then the second term (Vwithin/n) in the expression for SDD would tend to zero. The uncertainty about the adequacy of the individual 's intake would result primarily from not knowing where in the distribution of requirements that individual's unobservable requirement ρ is located. The degree of uncertainty about adequacy would then be proportional to the variability of requirements in the group.
-
If the individual were to consume the same diet day after day, then the second term (Vwithin/n) would again be very small, even with small n, because the variability in intakes from day to day would be very small for that individual. Again, the uncertainty about the
-
adequacy of the individual's intake would reflect the uncertainty about that individual's requirement for the nutrient.
-
Hypothetically, if an individual's requirement could be observed, then the first term in the expression for SDD would be zero, and the uncertainty would reflect only the fact that the individual's usual intake for the nutrient cannot be observed.
The three situations above are extreme and typically do not occur. A more common situation is when there is some information about the individual's daily intake (allowing for an estimate of ӯ) and some idea of the distribution of requirements in the group. For example, the median requirement (EAR) and the coefficient of variation (CV) of requirements might be known, allowing the SDr to be derived.
Suppose that a level of confidence of at least 85 percent is desired before concluding that an individual's usual intake is adequate. To find out how large the ratio D/SDD would need to be to reach this conclusion, compare the D/SDD to the z-values listed in a standard z-table (e.g., a value of 0.85 in the table corresponds to a z-value of 1). Thus, if the ratio D/SDD is approximately equal to 1, it can be concluded with an 85 percent level of confidence that the individual's usual intake is larger than the requirement. Selected z-values, corresponding to different levels of assurance, are given in Table B-1. The criterion for using the ratio D/SDD and the qualitative conclusions from the quantitative analysis can be summarized as follows:
-
If D/SDD is greater than 1, then there is reasonable certainty that the individual 's usual intake is adequate. In other words, it is reasonably certain that the unobservable true difference between the individual's usual intake and requirement (y − ρ) is positive and thus the individual's usual intake exceeds requirement.
-
If D/SDD is less than −1, then it is reasonably certain that the individual's usual intake is inadequate. In other words, the true difference between the individual's usual intake and requirement (y − ρ) is negative and thus the individual's usual intake is less than the requirement.
-
If D/SDD is anywhere between −1 and 1, it cannot be determined with certainty whether the individual 's intake is adequate or inadequate.
The criterion above is derived by using principles from hypothesis testing and construction of confidence intervals under normality
TABLE B-1 Values for the Ratio D/SDD and Corresponding Probability of Correctly Concluding that Usual Intake Is Adequate or Inadequate
|
Criterion |
Conclusion |
Probability of Correct Conclusion |
|
D/SDD > 2.00 |
Usual intake is adequate |
0.98 |
|
D/SDD > 1.65 |
Usual intake is adequate |
0.95 |
|
D/SDD > 1.50 |
Usual intake is adequate |
0.93 |
|
D/SDD > 1.00 |
Usual intake is adequate |
0.85 |
|
D/SDD > 0.50 |
Usual intake is adequate |
0.70 |
|
D/SDD > 0.00 |
Usual intake is adequate (inadequate) |
0.50 |
|
D/SDD < −0.50 |
Usual intake is inadequate |
0.70 |
|
D/SDD < −1.00 |
Usual intake is inadequate |
0.85 |
|
D/SDD < −1.50 |
Usual intake is inadequate |
0.93 |
|
D/SDD < −1.65 |
Usual intake is inadequate |
0.95 |
|
D/SDD < −2.00 |
Usual intake is inadequate |
0.98 |
|
SOURCE: Adapted from Snedecor and Cochran (1980). |
||
and is only approximate. The assumptions that are implicit in the criterion include:
-
The distribution of daily intakes Y around the mean intake
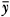 is approximately normal, or at least symmetrical, for the individual. Any nutrient with a skewed distribution of daily intakes would not satisfy this assumption, such as those nutrients in Table B-2, Table B-3, Table B-4 through Table B-5 with a CV larger than about 60 to 70 percent.
is approximately normal, or at least symmetrical, for the individual. Any nutrient with a skewed distribution of daily intakes would not satisfy this assumption, such as those nutrients in Table B-2, Table B-3, Table B-4 through Table B-5 with a CV larger than about 60 to 70 percent. -
The distribution of requirements in the group is approximately normal.
-
The daily intake Y accurately reflects the individual's true intake of the nutrient for the day.
-
A reliable estimate of the day-to-day variability in intake for the individual is available.
-
Intakes are independent of requirements.
In probabilistic terms, the value of 1 for the ratio D/SDD corresponds to an approximate 0.15 p-value for the test of the hypothesis that y > ρ. That is, when it is concluded that intake is adequate, there is approximately an 85 percent chance of reaching the correct conclusion and approximately a 15 percent chance of making a mistake (erroneously concluding that intake is adequate). Because the criterion is formulated on this probabilistic basis, the level of
TABLE B-2 Estimates of Within-Subject Variation in Intake, Expressed as Standard Deviation (SD)a and Coefficient of Variation (CV) for Vitamins and Minerals in Adults Aged 19 and Over
|
Nutrientb |
Adults Ages 19–50 y |
Adults, Ages 51 y and Over |
||||||
|
Females (n = 2,480)c |
Males (n = 2,538) |
Females (n = 2,162) |
Males (n = 2,280) |
|||||
|
CV |
CV |
CV |
CV |
|||||
|
SD |
(%) |
SD |
(%) |
SD |
(%) |
SD |
(%) |
|
|
Vitamin A (μg) |
1,300 |
152 |
1,160 |
115 |
1,255 |
129 |
1,619 |
133 |
|
Carotene (RE) |
799 |
175 |
875 |
177 |
796 |
147 |
919 |
153 |
|
Vitamin E (mg) |
5 |
76 |
7 |
176 |
6 |
65 |
9 |
60 |
|
Vitamin C (mg) |
73 |
87 |
93 |
92 |
61 |
69 |
72 |
71 |
|
Thiamin (mg) |
0.6 |
47 |
0.9 |
46 |
0.5 |
41 |
0.7 |
40 |
|
Riboflavin (mg) |
0.6 |
50 |
1.0 |
44 |
0.6 |
42 |
0.8 |
40 |
|
Niacin (mg) |
9 |
47 |
12 |
44 |
7 |
42 |
9 |
39 |
|
Vitamin B6 (mg) |
0.8 |
53 |
1.0 |
48 |
0.6 |
44 |
0.8 |
42 |
|
Folate (μg)d |
131 |
62 |
180 |
61 |
12 |
52 |
150 |
53 |
|
Vitamin B12 (μg) |
12 |
294 |
13 |
212 |
10 |
237 |
14 |
226 |
|
Calcium (mg) |
325 |
51 |
492 |
54 |
256 |
44 |
339 |
44 |
|
Phosphorous (mg) |
395 |
39 |
573 |
38 |
313 |
33 |
408 |
32 |
|
Magnesium (mg) |
86 |
38 |
122 |
38 |
74 |
33 |
94 |
32 |
|
Iron (mg) |
7 |
53 |
9 |
51 |
5 |
44 |
7 |
44 |
|
Zinc (mg) |
6 |
61 |
9 |
63 |
5 |
58 |
8 |
66 |
|
Copper (mg) |
0.6 |
53 |
0.7 |
48 |
0.5 |
53 |
0.7 |
56 |
|
Sodium (mg) |
1,839 |
44 |
1,819 |
43 |
1,016 |
41 |
1,323 |
38 |
|
Potassium (mg) |
851 |
38 |
1,147 |
36 |
723 |
31 |
922 |
31 |
|
NOTE: When the CV is larger than 60 to 70 percent the distribution of daily intakes is nonnormal and the methods presented here are unreliable. a Square root of the residual variance after accounting for subject, and sequence of observation (gender and age controlled by classifications). b Nutrient intakes are for food only, data does not include intake from supplements. c Sample size was inadequate to provide separate estimates for pregnant or lactating women. d Folate reported in μg rather than as the new dietary folate equivalents (DFE). SOURCE: Data from Continuing Survey of Food Intakes by Individuals1994–1996. |
||||||||
certainty can be adjusted by either increasing or decreasing the value of the cutoff for D/SDD (e.g., if 0.5 or −0.5 was used, then the level of certainty would decrease to about 70 percent). Table B-1 indicates the probability, or level of certainty, of correctly concluding that the usual intake is adequate (or inadequate) when D/SDD ranges from 2.00 to −2.00.
TABLE B-3 Estimates of Within-Subject Variation in Intake, Expressed as Standard Deviation (SD)a and Coefficient of Variation (CV) for Vitamins and Minerals in Adolescents and Children
|
Nutrientb |
Adolescents, Ages 9–18 y |
Children, Ages 4–8 y |
||||||
|
Females (n = 1,002) |
Males (n = 998) |
Females (n = 817) |
Males (n = 883) |
|||||
|
CV |
CV |
CV |
CV |
|||||
|
SD |
(%) |
SD |
(%) |
SD |
(%) |
SD |
(%) |
|
|
Vitamin A (μg) |
852 |
109 |
898 |
91 |
808 |
103 |
723 |
86 |
|
Carotene (RE) |
549 |
180 |
681 |
197 |
452 |
167 |
454 |
166 |
|
Vitamin E (mg) |
4 |
67 |
5 |
62 |
3 |
54 |
3 |
57 |
|
Vitamin C (mg) |
81 |
90 |
93 |
89 |
61 |
69 |
74 |
76 |
|
Thiamin (mg) |
0.6 |
43 |
0.8 |
42 |
0.5 |
35 |
0.5 |
37 |
|
Riboflavin (mg) |
0.7 |
42 |
1.0 |
41 |
0.6 |
35 |
0.7 |
35 |
|
Niacin (mg) |
8 |
46 |
11 |
43 |
6 |
36 |
7 |
38 |
|
Vitamin B6 (μg) |
0.7 |
49 |
1.0 |
49 |
0.6 |
42 |
0.7 |
43 |
|
Folate (μg)c |
128 |
58 |
176 |
60 |
99 |
48 |
117 |
50 |
|
Vitamin B12 (μg) |
5.5 |
142 |
5.0 |
93 |
9.6 |
254 |
4.7 |
118 |
|
Calcium (mg) |
374 |
48 |
505 |
48 |
313 |
40 |
353 |
41 |
|
Phosphorous (mg) |
410 |
38 |
542 |
37 |
321 |
32 |
352 |
32 |
|
Magnesium (mg) |
86 |
41 |
109 |
39 |
61 |
31 |
71 |
33 |
|
Iron (mg) |
6 |
47 |
9 |
50 |
5 |
45 |
6 |
43 |
|
Zinc (mg) |
5 |
50 |
8 |
58 |
3 |
41 |
4 |
42 |
|
Copper (mg) |
0.5 |
52 |
0.6 |
48 |
0.4 |
47 |
0.4 |
41 |
|
Sodium (mg) |
1,313 |
45 |
1,630 |
42 |
930 |
38 |
957 |
35 |
|
Potassium (mg) |
866 |
41 |
1,130 |
41 |
631 |
32 |
750 |
35 |
|
NOTE: When the CV is larger than 60 to 70 percent the distribution of daily intakes is nonnormal and the methods presented here are unreliable. a Square root of the residual variance after accounting for subject, and sequence of observation (gender and age controlled by classifications). b Nutrient intakes are for food only, data does not include intake from supplements. c Folate reported in μg rather than as the new dietary folate equivalents (DFE). SOURCE: Data from Continuing Survey of Food Intakes by Individuals1994–1996. |
||||||||
Note that D/SDD depends on the size of the difference between observed mean intake and the EAR and the standard deviation of that difference. For very large differences between observed mean intake and the EAR, it is likely that the ratio will exceed 1 and usual intake exceeds requirement. For smaller differences, the ability to critically interpret individual dietary intake data depends on the standard deviation of the difference between the observed intake
TABLE B-4 Estimates of Within-Subject Variation in Intake, Expressed as Standard Deviation (SD)a and Coefficient of Variation (CV) for Macronutrients and Cholesterol in Adults Aged 19 and Over
|
Nutrientb |
Adults, Ages 19–50 y |
Adults, Ages 51 y and Over |
||||||
|
Females (n = 2,480)c |
Males (n = 2,583) |
Females (n = 2,162) |
Males (n = 2,280) |
|||||
|
CV |
CV |
CV |
CV |
|||||
|
SD |
(%) |
SD |
(%) |
SD |
(%) |
SD |
(%) |
|
|
Energy (kcal) |
576 |
34 |
854 |
34 |
448 |
31 |
590 |
29 |
|
Fat (total, g) |
29.9 |
48 |
42.7 |
44 |
24.0 |
45 |
31.8 |
42 |
|
Fat (saturated, g) |
10.9 |
52 |
15.9 |
49 |
8.6 |
50 |
11.4 |
45 |
|
Fat (mono-unsaturated, g) |
12.0 |
50 |
17.4 |
46 |
9.7 |
48 |
13.0 |
44 |
|
Fat (poly-unsaturated, g) |
8.4 |
64 |
11.3 |
59 |
7.0 |
61 |
8.8 |
57 |
|
Carbohydrate (g) |
75.2 |
35 |
109 |
35 |
59.9 |
32 |
79.5 |
32 |
|
Protein (g) |
26.6 |
42 |
40.4 |
41 |
22.1 |
37 |
28.6 |
35 |
|
Fiber (g) |
6.5 |
49 |
9.2 |
51 |
5.9 |
43 |
7.7 |
43 |
|
Cholesterol (mg) |
168 |
77 |
227 |
66 |
144 |
70 |
201 |
66 |
|
NOTE: When the CV is larger than 60 to 70 percent the distribution of daily intakes is nonnormal and the methods presented here are unreliable. a Square root of the residual variance after accounting for subject, and sequence of observation (gender and age controlled by classifications). b Nutrient intakes are for food only, data does not include intake from supplements. c Sample size was inadequate to provide separate estimates for pregnant or lactating women. SOURCE: Data from Continuing Survey of Food Intakes by Individuals1994–1996. |
||||||||
and the EAR. This standard deviation depends, among other factors, on the number of days of intake data that are available for the individual. The fewer days of intake data available for the individual, the larger the standard deviation of the difference (resulting in a smaller ratio D/SDD) and the lower the likelihood of being able to assess adequacy or inadequacy.
Implementation of the Individual Assessment Approach
To implement the approach described above, the following information is needed:
TABLE B-5 Estimates of Within-Subject Variation in Intake, Expressed as Standard Deviation (SD)a and Coefficient of Variation (CV) for Macronutrients and Cholesterol in Adolescents and Children
|
Nutrientb |
Adolescents Ages 9–18 y |
Children Ages 4–8 y |
||||||
|
Females (n = 1,002) |
Males (n = 998) |
Females (n = 817) |
Males (n = 833) |
|||||
|
CV |
CV |
CV |
CV |
|||||
|
SD |
(%) |
SD |
(%) |
SD |
(%) |
SD |
(%) |
|
|
Energy (kcal) |
628 |
34 |
800 |
33 |
427 |
27 |
478 |
27 |
|
Fat (total, g) |
29.8 |
45 |
38.2 |
42 |
21.3 |
37 |
23.9 |
37 |
|
Fat (saturated, g) |
11.3 |
48 |
15.3 |
48 |
8.5 |
40 |
9.6 |
40 |
|
Fat (mono-unsaturated, g) |
12.4 |
48 |
15.5 |
44 |
8.6 |
39 |
9.9 |
41 |
|
Fat (poly-unsaturated, g) |
7.3 |
60 |
8.7 |
55 |
5.1 |
52 |
5.5 |
52 |
|
Carbohydrate (g) |
88.1 |
35 |
113 |
35 |
61.7 |
29 |
70.8 |
30 |
|
Protein (g) |
26.2 |
42 |
33.9 |
39 |
19.2 |
34 |
20.4 |
33 |
|
Fiber (g) |
6.2 |
51 |
8.7 |
56 |
4.6 |
43 |
5.3 |
45 |
|
Cholesterol (mg) |
145 |
72 |
199 |
71 |
129 |
70 |
137 |
66 |
|
NOTE: When the CV is larger than 60 to 70 percent the distribution of daily intakes is nonnormal and the methods presented here are unreliable. a Square root of the residual variance after accounting for subject, and sequence of observation (gender and age controlled by classifications). b Nutrient intakes are for food only, data does not include intake from supplements. SOURCE: Data from Continuing Survey of Food Intakes by Individuals1994–1996. |
||||||||
-
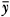 , the mean of n days of intake for the individual;
, the mean of n days of intake for the individual; -
SDwithin, the day-to-day standard deviation of the individual's intake for the nutrient;
-
EAR, the median nutrient requirement; and
-
SDr, the standard deviation of requirements in the group.
For nutrients that do not have an EAR, this approach cannot be used. (Guidance on how to assess an individual's usual intake by comparing it to the Adequate Intake [AI] is provided later in this appendix.) When an EAR for the nutrient is provided in a DRI report, the standard deviation of requirements is also available in the form of a coefficient of variation of requirement or percentage of the EAR. In most cases, it is assumed to be 10 percent.
The day-to-day standard deviation in intakes is harder to deter-
mine because data that permit the calculation are scarce. Using data collected in the Beltsville One Year Dietary Survey (Mertz and Kelsay, 1984), Tarasuk and Beaton (1992) investigated intake patterns for several nutrients and produced estimates of, among other parameters, the day-to-day variance in intakes for those nutrients. Other estimates have been developed from research databases and from large survey data sets with replicate observations (e.g., the Continuing Survey of Food Intakes by Individuals [CSFII]). Table B-2, Table B-3, Table B-4 through Table B-5 present pooled estimates of the day-to-day variance in intakes based on an analysis of the 1994–1996 CSFII data. Since a reliable estimate of the day-to-day variability in intakes for a specific individual is not typically available, the pooled estimates in Table B-2, Table B-3, Table B-4 through Table B-5 should be used. This introduces other uncertainties, however.
Limitations of Using the EAR for Individual Assessment
The method described to compare an individual's observed intake to the EAR for the purpose of drawing conclusions about the usual intake of the individual cannot be implemented in all cases. Even when the appropriate calculations are carried out, incorrect conclusions may result if estimates of the SD of daily intake and the SD of requirements are incorrect. These two situations are discussed below.
The SD of Intake for the Individual Is Not Equal to the Pooled Estimate Obtained from CSFII or from the National Health and Nutrition Examination Survey
The value of the ratio D/SDD critically depends on the SD of daily intake for the individual. It is recommended that the estimate obtained from CSFII (see Table B-2, Table B-3, Table B-4 through Table B-5) be used for all individuals, even though it has been argued that the day-to-day variability in intakes is typically heterogeneous across individuals. Several researchers, including Tarasuk and Beaton (1992), have argued that day-to-day variability in intakes varies across individuals (see also Nusser et al., 1996); therefore a pooled variance estimate as suggested here might not be the optimal strategy. In theory, if many days of intake data Yj were available for an individual, the within-individual variance in intakes could be computed in the standard manner:
where Yj denotes the intake for the individual observed on the jth day and ![]() is the mean of the n days of observed intakes. The within-individual standard deviation SDwithin is computed as the square root of Vwithin. Unless a large number of nonconsecutive days (e.g., more than 10 or 12 days) of intake records are available for the individual, it is recommended that the pooled estimate from Table B-2, Table B-3, Table B-4 through Table B-5 be used instead. Whereas this pooled estimate is likely to be incorrect for the individual, at this time there is no better alternative. More research is needed in this area that will permit estimating an adjustment of the pooled variance estimate to suit a particular individual.
is the mean of the n days of observed intakes. The within-individual standard deviation SDwithin is computed as the square root of Vwithin. Unless a large number of nonconsecutive days (e.g., more than 10 or 12 days) of intake records are available for the individual, it is recommended that the pooled estimate from Table B-2, Table B-3, Table B-4 through Table B-5 be used instead. Whereas this pooled estimate is likely to be incorrect for the individual, at this time there is no better alternative. More research is needed in this area that will permit estimating an adjustment of the pooled variance estimate to suit a particular individual.
The Day-To-Day Distribution of Intakes Is Not Normal
The assumption of normality (or near normality) of the observed intakes Yj is critical, as the proposed approach relies on normality of the difference D. Normality of D will not be satisfied whenever the observed intakes Yj (and consequently, the observed intake mean) are not normally distributed. How does one decide whether the distribution of observed intakes for an individual is approximately normal? Typically there are not enough days of intake data available for an individual to be able to conduct a test of normality of the observed intakes. Therefore, one must rely on the CV of daily intakes that are presented in Table B-2, Table B-3, Table B-4 through Table B-5.
As a rule, any nutrient with a CV above 60 to 70 percent should be considered to have a nonnormal distribution for the following reason: if daily intakes for an individual are normally distributed, then subtracting 2 SD of intake from the individual's mean should still result in a positive value, as intakes are restricted to being positive. Suppose that the CV of intake was 60 percent, then the SD of intake is 0.6 × mean intake. If 2 SDs of intake are now subtracted from the individual 's mean intake a negative value is obtained, indicating that the distribution of observed intakes around the individual's usual intake is not normal.
Mean intake − 2 SD intake = mean intake − 2 × 0.6 × mean intake
= mean intake − 1.2 mean intake
= −0.2 × mean intake.
The value in the last equation is negative, suggesting that the normal model is not reasonable when the CV of intake is above 60 to 70 percent.
Data presented in Table B-2, Table B-3, Table B-4 through Table B-5 indicate that it is not possible to use this approach to assess the adequacy of vitamin A, vitamin C, vitamin E, and some other nutrients. In these cases, the distribution of daily intakes cannot be assumed to be normal, and thus observed daily intake cannot be used to carry out the assessment.
Because the distributions of daily intake for many nutrients are nonnormal, more research is needed in order to extend this methodology to all nutrients of interest.
Requirement Distribution Is Not Normal
The proposed approach relies also on normality of the requirement distribution. When requirements are not distributed in a symmetrical, approximately normal fashion around the EAR, results may be biased. For example, the confidence with which it can be concluded that intake is adequate may be less than 85 percent even though the observed ratio D/SDD is equal to 1.
Iron is an example of a nutrient for which the distribution of requirements is not normal. Iron requirements in menstruating women are skewed, with a long tail to the right. In this situation, the method described above does not produce reliable results. No alternative can be offered at this time; more research is needed in this area.
Incorrect Specification of the SD of Requirement
Until now, little if any attention has been paid to reliably estimating the variance of nutrient requirement distributions. DRI reports (IOM, 1997, 1998b, 2000) have assumed that the CV of requirements for most nutrients is 10 percent of the EAR, unless other information is known (e.g., niacin is given as 15 percent). Given an EAR and a CV of requirement, an SD of requirement can be calculated as SDr = CV × EAR. For example, if the EAR of a nutrient is 120 units/day and the CV of requirement is 10 percent, then the SD of requirement will be 0.1 × 120 = 12 units/day.
It is not clear that the fixed 10 percent (or 15 percent) CV estimates across nutrients result in reliable estimators of the SD of requirement. Since the SD of requirement is an important component of the SD of D, an inaccurate value of SDr will result in an inaccurate value of SDD and hence an inaccurate value of the ratio D/SDD.
At this time, no better alternatives than using the CV of the requirement as given in the DRI reports have been identified, and thus the results of such analyses should be interpreted with caution.
INDIVIDUAL ASSESSMENT FOR NUTRIENTS WITH AN AI
Before discussing a statistical approach to individual assessment for nutrients with an Adequate Intake (AI) instead of an Estimated Average Requirement (EAR), it is critical to emphasize the difference between these two Dietary Reference Intakes (DRIs). The EAR represents the median nutrient requirement of a given life stage and gender group, and by definition, an intake at the level of the EAR will be inadequate for half the group. In contrast, the AI represents an intake that is likely to exceed the actual requirements of almost all healthy individuals in a life stage and gender group. In this respect it is analogous to the Recommended Dietary Allowance (RDA); however, because of the imprecise nature of the data used to establish AIs, it may often be higher than an RDA would be if appropriate data were available to calculate one.
The approach discussed previously to assess nutrient adequacy compares an individual's intake to the EAR, and considers variability in both intake and requirement when determining how confident one can be in concluding that intake is adequate. In other words, intakes are compared to median requirements. In the case of the AI, however, intakes are compared to an intake value already in excess of the median requirement, perhaps by a very large margin. Thus, when intakes are compared to the AI, all one can truly conclude is whether intake is above the AI or not. Although an intake that is statistically above the AI is certainly adequate, intakes below the AI are also likely to be adequate for a considerable proportion of individuals. Thus, great caution must be exercised when interpreting intakes relative to AIs.
How can individual assessment be carried out when the nutrient of interest does not have an EAR? Using calcium as an example, one is limited to comparing the individual's usual intake to the AI. The conclusions that can be drawn from such a comparison are rather narrow: if the usual intake is determined with desired accuracy to be larger than the AI, then the individual's usual intake of the nutrient is likely to be adequate. The converse, however, is not true. At the desired level of confidence, nothing can be concluded from the analysis if it is found that the individual's usual intake is not larger than the AI.
A simple z-test to decide whether an individual's unobservable usual intake is larger than the AI can be used. The test assumes that daily intakes for an individual have a distribution that is approximately normal around the individual's usual intake. The SD of daily intake is necessary to carry out the test. Because large numbers of
daily intakes for an individual are typically not available to reliably estimate the day-to-day variability, the pooled day-to-day SD of intake from CSFII (see Table B-2, Table B-3, Table B-4 through Table B-5) or from NHANES is used.
The z-statistic is constructed as follows:
z = ![]() × (observed mean intake − AI)/SD of daily intake.
× (observed mean intake − AI)/SD of daily intake.
By rearrangement, this can also be expressed as:
z = (observed mean intake − AI) / (SD of daily intake/ ![]() ).
).
The z-statistic is then compared to tabulated values (a selection of which are presented in Table B-6), to decide whether the desired level of accuracy is achieved when stating that the usual intake is larger than the AI.
For example, consider a nutrient such as calcium with an AI of 1,000 mg /day, and suppose that the SD of daily intake from CSFII for the appropriate life stage and gender group is 325 mg/day.
TABLE B-6 Selected Values of z and the Associated Level of Confidence When Concluding That Individual Usual Intake Is Larger Than the Adequate Intake (AI) or Less Than the Tolerable Upper Intake Level (UL)
|
Criterion |
Conclusion |
Probability of Correct Conclusion |
|
z > 2.00 |
Usual intake is adequate (excessive) |
0.98 |
|
z > 1.65 |
Usual intake is adequate (excessive) |
0.95 |
|
z > 1.50 |
Usual intake is adequate (excessive) |
0.93 |
|
z > 1.25 |
Usual intake is adequate (excessive) |
0.90 |
|
z > 1.00 |
Usual intake is adequate (excessive) |
0.85 |
|
z > 0.85 |
Usual intake is adequate (excessive) |
0.80 |
|
z > 0.68 |
Usual intake is adequate (excessive) |
0.75 |
|
z > 0.50 |
Usual intake is adequate (excessive) |
0.70 |
|
z > 0.00 |
Usual intake is adequate (excessive/safe) |
0.50 |
|
z > −0.50 |
Usual intake is adequate (excessive) |
0.30 (0.70 probability usual intake is safe) |
|
z > −0.85 |
Usual intake is adequate (excessive) |
0.20 (0.80 probability usual intake is safe) |
|
z > −1.00 |
Usual intake is adequate (excessive) |
0.15 (0.85 probability usual intake is safe) |
|
SOURCE: Adapted from Snedecor and Cochran (1980). |
||
Given five individuals, each with three days of intake records and observed mean intakes of 1,050, 1,150, 1,200, and 1,250 mg/day, respectively, what can be determined about the adequacy of their usual intakes? Assume that, to determine if the usual intake is higher than the AI, a minimum confidence level of 85 percent is desired.
To calculate the z-values for each of the five individuals, first divide the SD of daily intake by the ![]() (as 3 daily records are available for each). In this example, 325/
(as 3 daily records are available for each). In this example, 325/ ![]() equals 188. The z-values are now computed as (observed mean intake − AI)/188. For the five individuals, the corresponding z-values are 0.27, 0.53, 0.80, 1.07, and 1.33, respectively. From a standard z-table the probabilities of correctly concluding that the usual intake is larger than the AI for each of the five individuals are 61, 70, 79, 86, and 91 percent, respectively. Only for the last two individuals, with observed mean intakes of 1,200 and 1,250 mg /day, would there be an 85 percent confidence level when stating that usual intakes are greater than 1,000 mg/day.
equals 188. The z-values are now computed as (observed mean intake − AI)/188. For the five individuals, the corresponding z-values are 0.27, 0.53, 0.80, 1.07, and 1.33, respectively. From a standard z-table the probabilities of correctly concluding that the usual intake is larger than the AI for each of the five individuals are 61, 70, 79, 86, and 91 percent, respectively. Only for the last two individuals, with observed mean intakes of 1,200 and 1,250 mg /day, would there be an 85 percent confidence level when stating that usual intakes are greater than 1,000 mg/day.
The value of the z-statistic will increase whenever
-
the difference between the observed mean intake and the AI increases;
-
the SD of daily intake for the nutrient is low; and
-
the number of days of intake data available for the individual increases.
This z-test relies on the assumption of normality of daily intakes. For nutrients such as vitamin A, vitamin B12, and others with a CV of daily intake larger than 60 to 70 percent, this test is likely to perform poorly. While the calculations are still possible, the level of assurance resulting from the test will be incorrect. The performance of the test also depends on accurately estimating the day-to-day variability in intakes for the individual. It is suggested that the pooled SD of daily intake obtained, for example, from Table B-2, Table B-3, Table B-4 through Table B-5 be used in the calculations even though it is likely to be a poor estimate of the individual's true day-to-day variability in intakes. As stated earlier, a more justifiable alternative cannot be offered at this time, as no extensive studies on the dependence of individual SD of intake and individual mean intake have been published. More research is needed in this area.
ASSESSING EXCESSIVE INTAKE AT THE INDIVIDUAL LEVEL
Evaluation of the adequacy of an individual's usual intake of a nutrient has been discussed. Since food fortification is now commonplace and supplement intake is also on the rise, it is important to evaluate whether an individual's usual intake of a nutrient might be excessive. To decide whether an individual has chronic consumption of a nutrient at levels that may increase the risk of adverse effects, the usual nutrient intake is compared to the Tolerable Upper Intake Level (UL) established for the nutrient.
Because usual intakes are unobservable, the uncertainty of how well observed mean intake estimates usual intake must be accounted for, similar to comparing intake to the Adequate Intake (AI) as discussed in the previous section. In this case, however, the z-statistic is constructed by subtracting the UL from the observed mean intake, and dividing the difference by the SD of daily intake over the square root of the number of days of intake available for the individual.
z = (observed mean intake − UL) / (SD of daily intake/ ![]() )
)
The resulting z-statistic is compared to tabulated values (Table B-6), and the confidence level associated with the conclusion that the usual intake is below the UL is obtained. If the resulting confidence level is at least as high as the desired level, then it can be concluded that the individual's usual intake of the nutrient is below the UL and thus a tolerable level of intake for the individual. If the resulting confidence level is not as high as the desired level, then it cannot be conclusively stated that intake is risk free.
Caution also applies in this case. The z-test performs well when daily intakes are approximately normally distributed, but may give incorrect confidence levels when the distribution of daily intakes departs from the normal. The SD of daily intake should accurately reflect the day-to-day variability in intakes for the individual. In the absence of better information about individual SD of daily intake, it is recommended that the pooled estimate of the SD of intake computed from a large nationwide food consumption survey be used. Use of this pooled estimate of the SD of daily intakes is not ideal for the individual, but a reliable alternative is not available at this time.
In the case of regular supplement users, an overestimate of the individual day-to-day variability of intakes may result. If the day-to-day variability for a supplement user were smaller, then the z-statistic obtained from the assessment would be an underestimate.
When using the proposed method it is important to note that the pooled estimates of the within-person standard deviation of intakes in Table B-2, Table B-3, Table B-4 to Table B-5 are based on data on nutrients from food only, not food plus supplements. This suggests the need for caution in using these estimates in assessing individual intakes relative to the UL. For some nutrients, ULs are defined on the basis of total intake (food plus supplements), and the estimates of the within-person standard deviation of intakes based on food alone may not be the same as those based on food plus supplements. For other nutrients, ULs refer only to nutrient intake from food fortificants, supplements, and pharmacological products. In these cases, the proposed methods are even less reliable, as currently there are no estimates of the within-person standard deviation of intakes from supplement use alone.


















