3
Topological Twistronics
In the workshop’s third presentation, Jennifer Cano from Stony Brook University spoke about work that was motivated by the results in twisted bilayer graphene that had been described in the first two talks but which was otherwise significantly different. In particular, she discussed what might result from introducing a superlattice potential on the surface of a three-dimensional topological insulator (3D TI).
So why, she asked, would someone want to do this? Her motivation has its roots in some ab initio calculations on bismuth selenide, a topological insulator, showing that it had a single Dirac cone on its surface (Zhang et al. 2009). And that Dirac cone looks just like the Dirac cone in graphene, Cano said, except that the indices mean something completely different—spin up and spin down instead of the A and B sublattices in twisted graphene. “So,” she continued, “at least in the most naïve sense, if you were to make a twisted heterostructure of 3D TIs, you should be able to see some of the same phenomenology that you see in twisted bilayer graphene.” In particular, twisted bilayer graphene provides a tunable platform for creating interesting correlated phases of many different types. So Cano’s question by analogy is whether there is a tunable route to interaction-driven topological phases. “If we could get a flat band in this system,” she asked, “then would we be able to realize topological superconductivity, something that’s been sought after for a long time and is very difficult to realize? That’s our motivation.”
Among the various differences between twisted bilayer graphene and this 3D TI system, one in particularly important, Cano said: It is impossible to realize isolated flat bands in the 3D TI system. As the previous speakers had shown, in twisted bilayer graphene the bands are not only flat but they are isolated—there
are bandgaps above and below the conduction and valence bands. “We can’t get that for 3D TI because we can’t gap the surface Dirac cone,” she said. “That’s one of the fundamental principles of being a topological phase.”
Still, she continued, it might be possible to engineer this Dirac cone—to flatten it or rearrange it in some way—and that could be interesting. From a mean field perspective, there is evidence that if the Dirac cone could be flattened—that is, if the velocity of the Dirac cone was reduced, thus enhancing the density of states near the charge neutrality point—“then you would have an increased propensity of moving into an interacting phase.” A number of papers have suggested the possibility of superconducting and magnetic phases driven by interactions on the surface of a 3D TI, and those phases are more likely with a more shallow Dirac cone (Baum and Stern 2012; Das Sarma and Li 2013; Marchand and Franz 2012; Santos et al. 2010; Schmidt 2012; Sitte et al. 2013). That is one of the phenomena her group is interested in.
In particular, one of the things she has studied is how having a superlattice potential on the surface of a 3D TI affects its band structure and density of states. “We are not yet studying the interaction effects,” she said. “We just want to know what happens to the band structure and if there is some reason to study the system further. We see this as a starting point for understanding what could happen in these types of topological moiré heterostructures.”
Cano described two potential routes to realizing a moiré superlattice on the surface of a topological insulator (see Figure 3-1). The first route would be to put a 3D TI on top of a patterned dielectric. That would make it possible to directly
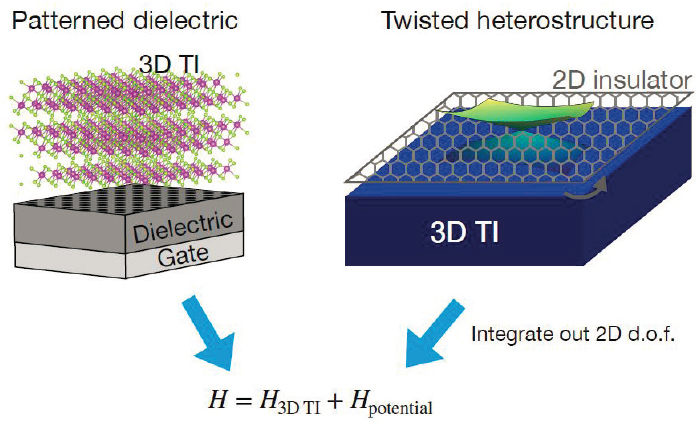
SOURCE: Jennifer Cano, Stony Brook University, presentation to the workshop, May 18, 2021; reprinted with permission from J. Cano, S. Fang, J.H. Pixley, and J.H. Wilson, 2021, “Moiré Superlattice on the Surface of a Topological Insulator,” Physical Review B 103(15):155–157, https://doi.org/10.1103/PhysRevB.103.155157, © 2021 by the American Physical Society.
apply the potential to the 3D TI with some superlattice modulation. Route 2 would be to make some kind of twisted heterostructure. That is a bit more speculative, she said, but the idea would be to start with a 3D TI and place a two-dimensional layer on top of that which is lattice-matched to the topological insulator. “Then we can twist the 2D layer and get a moiré heterostructure similar to the twisted bilayer graphene,” she said. “And if this 2D layer is an insulator, then we can integrate out the gap degrees of freedom, and we will be left with a super-lattice potential on the surface of the 3D TI.”
From a theoretical perspective, the two approaches provide basically the same Hamiltonian, which is a combination of the Hamiltonians of the 3D TI and the Hamiltonian of a potential on the surface of that topological insulator. “So that’s the basic Hamiltonian we want to study,” she said, and to do that she would analyze the Hamiltonian with a continuum model, a tight-binding model, and ab initio calculations.
ANALYZING A TWISTED HETEROSTRUCTURE
As context for analyzing a twisted heterostructure using those three approaches, Cano briefly reviewed the situation with twisted bilayer graphene, as had been described earlier in the workshop by Pablo Jarillo-Herrero. According to the Bistritzer–MacDonald model, the appearance of flat bands in twisted bilayer graphene can be understood through the leading order in perturbation theory. The basic idea, Cano said, is that all of the low-energy physics is captured by the Dirac cones, which cross at some point, but because of the interlayer coupling, that crossing is gapped, and then at the magic angles, where the size of the gap approaches the energy scale of the crossing point, the flat bands appear. And this same idea can be applied to Dirac cones on the surface of a 3D TI.
She illustrated how this analogue of the Bistritzer–MacDonald model appears in the case of a superlattice potential on a 3D TI (see Figure 3-2). The original Dirac cone is shown at the far left of the figure. It will have some potential applied, and that potential has superlattice wave vectors indicated by Qx and Qy. The potential acts to couple opposite sides of the Dirac cone and, in essence, folds up the typical-looking Dirac cone on the left to the folded Dirac cone in the middle. And that folded version includes not only the original Dirac cone (Γ0), whose velocity has changes, but also a number of other Dirac cones (Γ–1, Γ1, Γ2) that form at different energies. These “satellite Dirac cones” occur at energies away from the charge neutrality point.
Unlike the Dirac cones that appear in twisted bilayer graphene, Cano said, these satellite Dirac cones are protected by time-reversal symmetry because they are connecting time-reversed partners. This in turn means that these gaps cannot open, which is how the bulk–boundary correspondence is preserved. In short, she said, “there can never be a full gap that can open in this system, and that’s because these satellite Dirac cones have to remain gapless.”
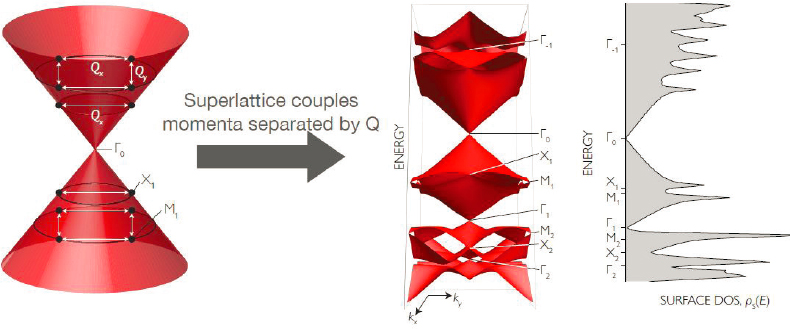
SOURCE: Jennifer Cano, Stony Brook University, presentation to the workshop, May 18, 2021; reprinted with permission from J. Cano, S. Fang, J.H. Pixley, and J.H. Wilson, 2021, “Moiré Superlattice on the Surface of a Topological Insulator,” Physical Review B 103(15):155–157, https://doi.org/10.1103/PhysRevB.103.155157, © 2021 by the American Physical Society.
The first question Cano asked about this system is what happens to the Dirac cone velocity in the presence of a superlattice potential. Calculations with a continuum model show that, to leading-order perturbation, the Dirac cone velocity gets renormalized. Specifically, the new velocity is equal, to leading order, to the old velocity divided by a factor of 1 + α, where α depends on potential strength and twist angle; specifically, α increases—and thus the Dirac cone velocity decreases—with increasing potential strength or decreasing twist angle. These are the same things that you see in twisted bilayer graphene, Cano said, but with a major difference: in this system, Dirac cone velocity can never be equal to zero. “If we ramp up the potential, we will just start slowly decreasing the velocity.”
It is also possible to use perturbation theory to compute the energies and velocities of the various satellite cones, Cano noted. And when you do, you find that some of them are isotropic, and some of them are anisotropic.
One concern with this approach of using perturbation theory in a continuum model, she said, is that it depends on various simplifications. It assumes, for instance, an isotropic Dirac cone that has no warping, but in reality the Dirac cones of bismuth selenide are not isotropic. Furthermore, the analysis involved only the surface Hamiltonian and completely ignored the bulk bands. So Cano’s next step was to discuss two three-dimensional lattice models of the system in order to see how well the perturbation theory performs and what happens when the analysis goes beyond first-order perturbation theory.
To do that she began with an analysis of one of the two systems she had mentioned earlier—the one consisting of a two-dimensional structure sitting on top
of a 3D TI. The 2D piece should be an insulator that is closely lattice-matched to the 3D TI, and the two lattices will be offset by a twist of a certain angle. In this situation there will be a Dirac cone on the surface of the topological insulator, and the two-dimensional material will have valence band that does not cross through the Dirac cone but is somewhat close. By integrating out the two-dimensional degrees of freedom to get the superlattice potential, one is left with a potential on the surface of our 3D TI whose strength depends not only on interlayer coupling but also on the separation between the top of the 2D valence band and the charge neutrality point of the Dirac cone. However, Cano said, the expression for the potential ends up being very complicated.
To deal with the complexity, Cano modeled the 3D TI on a square-lattice tight-binding model with a “twist potential.” It was a three-dimensional model with the potential on the surface, and she showed the full formula for the potential. “It’s a little complicated,” she said, “but on the other hand, it fits on one line and we will implement it on the computer, so it doesn’t really matter how complicated it is.”
Cano then displayed some of the results of those numerical calculations and compared them with the perturbation calculations (see Figure 3-3). In particular, she showed a plot of the velocity of the Dirac cone against the strength of the superlattice potential (see Figure 3-3, left-hand side). The first-order calculation with the perturbation theory matched the numerical calculations for small values of the potential, with the Dirac velocity decreasing as the strength of the potential
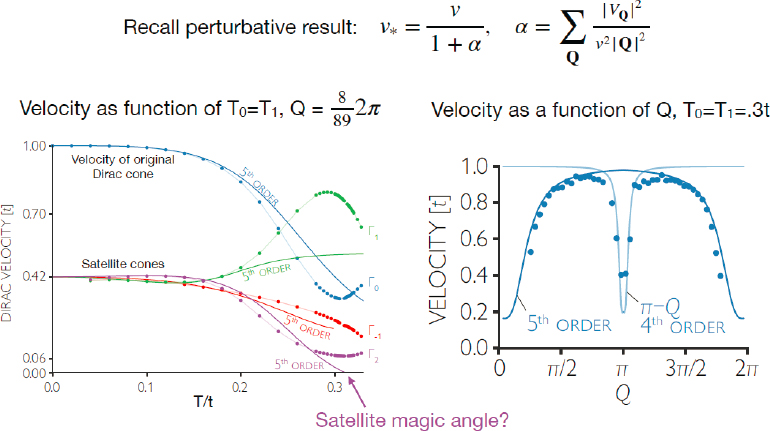
SOURCE: Jennifer Cano, Stony Brook University, presentation to the workshop, May 18, 2021.
increased. When perturbations up to fifth order were included, the perturbative result matched the numerical result very closely. In particular, she pointed out, the numerical results showed that the velocity of the Dirac cone drops down to a minimum of around 0.4 of the original value. “That’s actually a pretty substantial decrease in the Dirac cone velocity,” she said. “In terms of future directions, I think that’s very encouraging for asking how does the propensity to move into interacting topological phases change if you could tune the Dirac cone velocity by this amount.”
The velocities of the satellite cones do not have a pattern—some increase with increasing potential, while others decrease. Generally speaking, the perturbation theory captures this behavior reasonably well, agreeing with the numerical calculations for smaller potential values. In one case, Cano noted, the fifth-order perturbation calculation showed the velocity of a satellite cone going to zero, indicating a magic angle, but the numerical calculations showed that the velocity of the Dirac cones never went to zero, so there were no magic angles for the original Dirac cone or the satellite cones.
Cano also showed a second plot, this one of the Dirac cone velocity as a function of the twist angle, Q (right-hand side of Figure 3-3). “When we have this 2D layer on top of the 3D TI surface, the relative twist angle generates the wave vectors and the potential,” she said. What the plot showed was that by varying the twist angle, the Dirac velocity could be decreased to about half of its original value, which was similar to the decrease in the Dirac velocity that could be accomplished by varying the superlattice potential. Dropping the Dirac velocity by approximately half “may be the best that we can do here,” she said.
A third graph showed plots of the full band structure in the moiré Brillouin zone. One interesting thing that happens, Cano said, is that as the potential is increased, the different satellite cones move around in energy by different amounts, which means that at some fine-tuned value, two satellite cones will pass through each other, and when this happens, it results in very flat bands. “This is not what we were searching for,” she said. “We were trying to re-normalize the original Dirac cone.” But this is an alternative route to flat bands.
Finally, Cano described the results of ab initio calculations for such a twisted heterostructure. She chose to examine hexagonal boron nitride (hBN) on top of bismuth selenide (Bi2Se3) because the two materials have a reasonably good lattice match. However, the calculations uncovered a problem: the wave vectors that get produced from this matching are too big. Given the Dirac cone, the wave vector needs to be small enough so that it does not mix the bulk and surface states, she said, or else “it will be a complete mess.” And with hBN on Bi2Se3 the wave vectors are too large. So, to make a more realistic model, she turned to the other option: putting the 3D TI (Bi2Se3) on top of a patterned dielectric.
ANALYZING A TOPOLOGICAL INSULATOR ON A PATTERNED DIELECTRIC
Patterning a potential on the surface of bismuth selenide has pros and cons, Cano said. “One pro is that it’s completely tunable and you can choose the shape and the strength of it,” she said. “The con is there are limitations on what you can do in practical terms.”
To carry out her ab initio calculations of the bismuth selenide on a patterned dielectric, Cano chose to model a slab of Bi2Se3 that was five quintuple layers thick. “That’s about as many as you need for the Dirac cones on opposite surfaces to remain gapless,” she said. To model this bulk material she used Wannierized tight-binding, which reproduces the low-energy physics and the surface Dirac cone well. On top of this Wannierization of the three-dimensional bulk material she imposed a hexagonal superlattice potential, so that there were three different wave vectors. “We have not optimized this,” she said. “It’s not clear what pattern and size would be best, and we chose the unit cell to be around 12 nm—something that we thought was roughly within experimental reach.”
Calculations performed on this model—of a superlattice potential on the surface of bismuth selenide—showed a number of things. First, as the potential strength increases, it pushes the Dirac cones around. The original Dirac cone ends up shifting up in energy, while the three lowest-energy satellite cones end up moving down in energy. A more interesting result, Cano said, is what happens to the velocity of the Dirac cones as the superlattice potential strength is increased. The velocity of the original Dirac cone drops down to about one-third of its original value. “This is quite neat because this is a real model which is actually using the surface states of bismuth selenide,” she said. “We don’t assume anything about them.” So it is possible to significantly change the velocity of the Dirac cones by adjusting the superlattice potential even though it is not possible to gap the material or make flat bands.
One other noteworthy result is that because of the sixfold symmetry—this does not happen with fourfold symmetry—one of the satellite cones has zero velocity. “It will ultimately have higher-order dispersion, but the linear dispersion is vanishing due to symmetry,” she said. “And so that might be another place where there could be flat bands.”
With that, Cano summarized her talk to that point. She was interested in what happens to a TI surface in a superlattice potential. In particular, what happens to the surface Dirac cone? Can it be flattened it in some way to enhance the surface density of states and favor different types of interacting instabilities? The answer, she found, is yes. She can decrease the velocity of the Dirac cone to one-half or one-third of its original value, “which is really powerful, even though you can’t get
flat bands.” Furthermore, she found different routes to increase the density of states that she was not expecting. By causing two satellite cones to align, it is possible to get really flat bands, which could provide a different way to increase the density of states. Also, there are some satellite cones that have zero velocity, which is another place where flatter bands might emerge (also see description of this work in Cano et al. 2021).
In the future, Cano says she is interested in possibly finding two-dimensional materials that might better match the surface of bismuth selenide or some other well-studied 3D TI. Also, she said, she has been thinking about gapless materials. “What if we just put graphene on top of the 3D TI? Then the Dirac cones of graphene and the Dirac cones of bismuth selenide can interact with each other, and there we can get a more legitimate twisted heterostructure.”
FUTURE DIRECTIONS
Cano spent the remainder of her talk speaking of future directions in the field beyond her work that she had described and beyond twisted bilayer graphene. “One of the things that could be interesting is how can we manipulate the surface states of 3D materials with these sorts of hetero structures?” she said. “Since I am really interested in topological materials, I’m always thinking from that framework. How can we change topological surface states?” And there are a number of different ways to approach that, she said.
For example, it is not possible to have a flat band on the surface of a 3D TI because the Dirac cone cannot be gapped, but if the time-reversal symmetry is broken, then that constraint is lifted. So, she suggested, perhaps having a magnetic two-dimensional material on top of a 3D TI would produce flat bands with some interesting spin structure. There are also non-topological materials that also have surface states, and these materials might offer another place in which to search for interesting material combinations beyond just the two-dimensional materials. “What are these surface states?” she asked. “Where is the low-energy physics? Can we realize any of the interesting combinations and symmetry?” For example, she said, it is possible to obtain various types of lattice symmetry on the surface of three-dimensional materials that cannot be realized in two-dimensional materials.
Next Cano spoke about about an “interesting direction” that her team has been working on and which they had just published a paper on arXiv (Wang et al. 2021). The group was exploring the chiral model in bilayer graphene that Ashvin Vishwanath had described in the previous presentation. One of the things that Cano’s group did was to use numerical calculations to look at the wave functions at different higher-order magic angles. She showed a plot of the wave function in real space just at the K point, with charge density maxima shown in red and minima in purple. “And in the chiral model, which is quite special, the minima are
exact zeros,” she said. “The charge density vanishes.” In particular, they observed an increasing number of zeros at the second and third magic angles, which is interesting for several reasons, she said. The thing that is perhaps most interesting, she said, is that there is an analogy that can be made to higher Landau levels. In the theory of regular Landau levels, each Landau level has a Chern number, and when one moves from the first to the second Landau level, the wave function has an increasing number of zeros—the same thing that Cano’s group was seeing in going from the first magic angle to the second and third magic angle. “So there’s an analogy to be made there,” she said, “and the reason I think this is interesting is if we fractionally fill these flat bands, what we know from quantum Hall physics is that fractionally filling flat bands at higher magic angles gives you different phases than if you fractionally fill the first flat band coming from the first Landau level.” This in turn leads her to speculate that fractionally filling the flat bands coming at the second or third magic angle might lead to different correlated phases. This is something her team plans to pursue in the future.
Concerning this system, Cano said there are two predictions that could be experimentally tested. First, a majority of the zeros are fixed—they do not move—so in an experiment that averaged over different K points, the zeros could be observed as a lack of charge, she said. “So this pattern of zeros is something that is a prediction that we are making—as you look at second and third magic angles, you should see this different pattern of charge minima and charge maxima. Furthermore, she said, around each of these zeros the angle of the wave function—the phase—rotates, and this rotating becomes larger as one moves to the higher magic angles. “So a second prediction we are making is there will be a circulation current which is coming from the wave function winding around these zeros and that circulating current increases as you go from first to second to third magic angle.”
Another set of issues arises from comparing superlattice potentials versus twisted heterostructures. Both of these things can give rise to extremely flat bands, Cano said, and both of them are also highly tunable, albeit in different ways. But the correlated phases observed in twisted heterostructures are not observed in a superlattice potential. Why not? “I don’t at the moment understand why, if we see all these interesting correlated phases in twisted bilayer graphene, we do not see these in materials with a superlattice potential,” she said. “I think maybe we haven’t found the optimal choice of materials. So I think this could be an interesting direction to go in that also offers a lot of tunability.”
Finally, Cano mentioned some directions to explore in three-dimensional twistronics. Echoing the previous two speakers, she mentioned the possibility of stacking multiple two-dimensional layers with twists each between each. There are two different goals here, she said. One is creating three-dimensional flat bands, which both Jarillo-Herrero and Vishwanath had mentioned. But a second is stacking the two-dimensional materials in order to manipulate the two-dimensional
physics—to manipulate the magic angles and to explore the phase diagram, the symmetries, and different combinations of materials. This could offer some interesting results, Cano said.
Finally, although she said she was not sure whether it would actually lead to anything interesting, Cano suggested looking at “proper 3D materials” with a twist. One could, for example, put two blocks of materials together that were offset by a twist and look at the interface to see if anything happened that was not seen in twisted bilayers of graphene or other two-dimensional materials. Another possibility would be to take a block of three-dimensional material and apply a torque between the two ends to twist the entire block. “Playing around with possibilities for proper 3D materials is an unexplored phase space,” she said, “but on the other hand maybe it’s not as interesting and we should exhaust the 2D materials first.”
QUESTION-AND-ANSWER SESSION
Following Cano’s talk there was a brief question-and-answer session devoted to her presentation, moderated by Kapitulnik. The first questioner commented that 3D TIs are very difficult to exfoliate down to thin layers and asked whether the ideas that Cano discussed apply to, for example, to tungsten ditelluride. Cano responded by first pointing out that the idea in her work was not to get a thin layer of 3D TI. She used a thick sample of the topological insulator and puts something twodimensional on it. It is necessary for the 3D TI to have a flat and uniform surface, which might be an obstacle for some 3D TIs. She continued that she thought that tungsten ditelluride can realize a 2D TI, which, she said, brings us an interesting question that she had not talked about: What happens if a quasi-periodic or superlattice potential is applied to a 2D TI? “We’re been working on this a little bit,” she said. “There’s evidence that you can manipulate the 1D edge states on the 2D TI by this process.” That is another very interesting direction to explore, she said.
Kapitulnik followed up by noting that in a 3D TI the topological surface is all around the material. So, he asked, “can you use both surfaces and have a structure that connects the top and the bottom through the surface states?” If the 3D TI is thin, Cano answered, then the top and bottom surface states will hybridize with each other, and it might be possible to do something clever by manipulating both the top and bottom of the surface and hybridizing them with each other.
Kapitulnik then passed along a question on a different part of Cano’s presentation: “In the numeric results for the renormalization of the original Dirac cone, we see the velocity increases again after a critical potential swing. Is there a simple way to understand this behavior?” Cano answered that she does not believe there is a simple way to understand it, but she added that she does not believe the behavior is particularly unusual because something very similar happens in twisted bilayer graphene, a completely different system.
REFERENCES
Baum, Y., and A. Stern. 2012. “Magnetic Instability on the Surface of Topological Insulators”. Physical Review B 85:121105.
Cano, J., S. Fang, J.H. Pixley, and J.H. Wilson. 2021. “Moiré Superlattice on the Surface of a Topological Insulator.” Physical Review B 103(15):155–157.
Das Sarma, S., and Q. Li. 2013. “Many-Body Effects and Possible Superconductivity in the Two-Dimensional Metallic Surface States of Three-Dimensional Topological Insulators.” Physical Review B 88:081404(R).
Marchand, D.J.J., and M. Franz. 2012. “Lattice Model for the Surface States of a Topological Insulator with Applications to Magnetic and Exciton Instabilities.” Physical Review B 86:155146.
Santos, L., T. Neupert, C. Chamon, and C. Mudry. 2010. “Superconductivity on the Surface of Topological Insulators and in Two-Dimensional Noncentrosymmetric Materials.” Physical Review B 81:184502.
Schmidt, M.J. 2012. “Strong Correlations at Topological Insulator Surfaces and the Breakdown of the Bulk-Boundary Correspondence.” Physical Review B 86:161110.
Sitte, M., A. Rosch, and L. Fritz. 2013. “Interaction Effects on Almost Flat Surface Bands in Topological Insulators.” Physical Review B 88:205107.
Wang, J., Y. Zheng, A.J. Millis, and J. Cano. 2021. “Chiral Approximation to Twisted Bilayer Graphene: Exact Intra-Valley Inversion Symmetry, Nodal Structure, and Implications for Higher Magic Angles.” arXiv 2010.03589v2.
Zhang, H., C.-X. Liu, X.-L. Qi, X. Dai, Z. Fang, and S.-C. Zhang. 2009. “Topological Insulators in Bi2Se3, Bi2Te3, and Sb2Te3 with a Single Dirac Cone on the Surface.” Nature Physics 5:438–442.











