4.1 EXPLOITING THE ADVANTAGES OF BOTTOM-UP CHEMICAL SYNTHESIS FOR CONSTRUCTING QUANTUM ARCHITECTURES
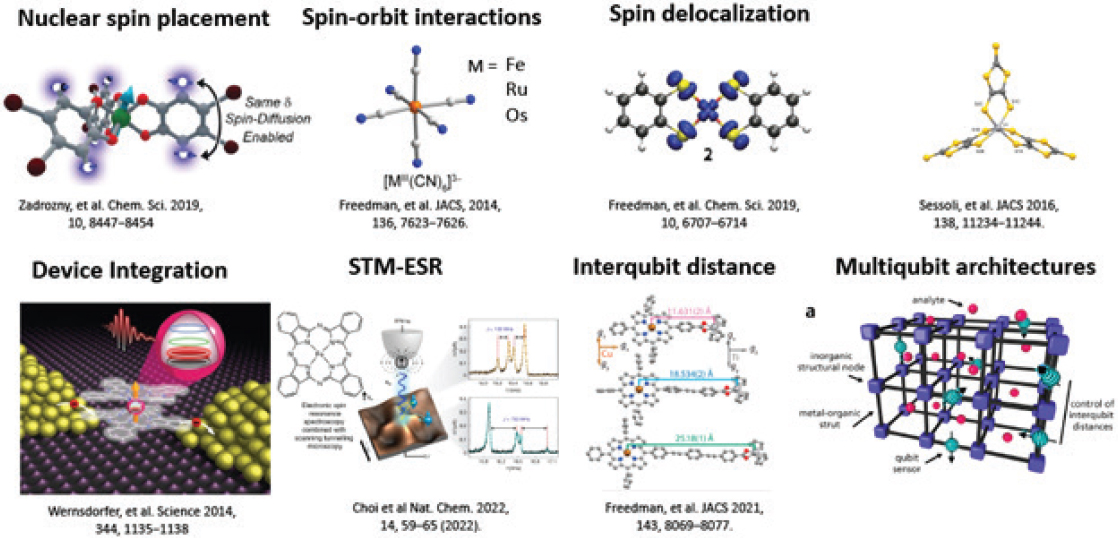
As discussed in Chapter 2, molecules offer an unmatched combination of atomic-scale tunability, portability, and scalability (Atzori and Sessoli 2019; Gaita-Ariño et al. 2019; Graham, Zadrozyn, et al. 2017; Jackson et al. 2021; Ye, Seo, and Galli 2019; C.-J. Yu et al.). With molecular chemistry, one can exploit the advantages used in medicinal chemistry for centuries—each molecule within a tablet of aspirin is chemically identical down to the sub-angstrom level and has the potential to maintain its fundamental characteristics in a wide range of chemical environments. This high level of structural precision combined with tunability makes molecules perfect for designer applications within QIS. Molecules can be tuned to have extrinsic compatibility with their environments for quantum sensing applications (Atzori and Sessoli 2019; Lovchinsky et al. 2016; C.-J. Yu et al. 2021). For example, they can be designed to be water soluble for integration into biological media or engineered to be compatible with surfaces. Their nanometer-scale size provides access to tiny sensing locations, as well as proximal placement within hybrid systems and spatial differentiation of sensor response. Furthermore, because molecules can be functionalized, they can be specifically tethered to an analyte, thereby enabling sub-diffraction imaging by initially identifying the molecule location and subsequently executing a quantum imaging experiment. Finally, molecular structures offer a unique means to address the scalability challenge of QIS: synthesizing large-scale, reproducible quantum states for applications from computing to communications (Figure 4-1). The aggregate of these attributes primes molecules to be key elements in the future quantum internet.
4.2 DEVELOPING TECHNIQUES FOR SYNTHESIZING MOLECULAR QUBITS THAT RETAIN THEIR DESIRABLE QUANTUM PROPERTIES IN DIFFERENT HOST CHEMICAL ENVIRONMENTS
For physical qubits to be useful, several challenges related to the underlying atomic-scale properties of the constituent materials must be addressed. First, it must be possible to fabricate large quantities of precise qubits reliably so that their functionality is known and largely retained upon synthesis or fabrication without the need for extensive characterization. Each of these qubits then needs to be entangled with other qubits and scaled up to construct larger, multiqubit systems. How can larger-scale quantum architectures be synthesized with sufficient control over disorder and decoherence? As pointed out in previous chapters of this report, loss of quantum coherence occurs during interactions between a qubit and its environment; decoherence processes need to be understood, controlled,
SOURCE: Atzori et al. 2016; Fataftah et al. 2019; Graham et al. 2014.; Jackson et al. 2019; von Kugelgen et al. 2021; Thiele et al. 2014; Zadrozny et al. 2017; Zhang et al. 2022.
and mitigated during each of these steps. Additionally, to build qubit architectures comprising dissimilar materials/chemistries (e.g., in hybrid quantum devices), heterogeneous interfaces between molecules and host materials need to be studied carefully and controlled. While current physical qubit proposals cover a spectrum of physical systems including molecular and solid-state spin centers (Miao et al. 2020), trapped ions (Bruzewicz et al. 2019; Georgescu 2020), superconducting (Devoret, Wallraff, and Martinis 2004), and topological systems (Freedman et al. 2003), all have decoherence and scaling issues that critically affect their potential as scalable, fault-tolerant systems. Exquisite control over constituent chemical environments at an atomic scale is central to understanding and controlling coherence and scaling in any qubit system. Chemists are needed at each step of this process:
- Synthesis or fabrication of high-quality, chemically precise molecules and materials that have near-optimal or tunable quantum properties across the range of quantum architectures;
- Development of a fundamental understanding of decoherence processes that arise from integrating molecular qubits into larger coherent quantum architectures;
- Design and synthesis of chemical environments that are robust to decoherence that can decouple the fundamental degrees of freedom of qubits from unwanted environment-induced noise;
- Bottom-up and top-down fabrication of heterogeneous material platforms that can transduce quantum information coherently from one chemical environment to another by leveraging surface chemistry and single-digit nanofabrication; and
- Design and fabrication of routes to couple physical qubit systems, especially molecules, that retain their quantum coherence but that can be patterned or arranged in repeatable, identical arrays.
Finally, while each of these steps is crucial for short- and long-term challenges in QIS, the ultimate goal is the fundamental design of precise, coupled, coherent physical qubit systems with on-demand properties for a specific quantum application. This can only be achieved through a concerted effort in chemical design, incorporating state-of-the-art synthesis, fabrication, characterization, and theory. Next, an overview of architecture-specific challenges to scaling is provided.
4.2.1 Investigating and Controlling the Interactions among Qubits and between Qubits and Their Environments
4.2.1a Chemical Design of Spin in Molecules
Several transition metal and f-block elements can serve as nuclear or electronic spin qubits. As described in Chapter 2, many promising examples of such systems, including nanomaterial–molecular (Rabl et al. 2010), nuclear-electronic spin (Abobeih et al. 2018), and light–matter hybrid (Ebbesen 2016) systems, have been published previously (Thiele et al. 2014). These studies exemplify how nuclear spins that can be used as quantum resources can be controlled through precise molecular design and synthesis (Sørensen et al. 2017). In fact, the ability to control the molecular environment around a metal atom can help to create a qubit with impressive insensitivity to the local environment. Systems in which the crystal field is tuned to create an avoided crossing “clock transition” with a large energy difference demonstrate the power of molecular design to create a robust qubit (Ishikawa, Sugita, and Wernsdorfer 2005; Kundu et al. 2022; McInnes 2022; Shiddiq et al. 2016). Scaling up systems to create arrays of molecular qubits requires a controlled synthesis with controllable inter-qubit distances. Examples of these types of controllable systems are metal–organic frameworks (MOFs) with constructions that are conducive to particular applications (Gaita-Ariño et al. 2019; Yamabayashi et al. 2018; Yu et al. 2020). More generally, interfacing tunable chemical ligands in scalable organic frameworks is already the focus of several classes of organic frameworks (MOFs along with hydrogen-bonded organic frameworks and covalent organic frameworks) and can potentially form highly ordered arrays.
4.2.1b Chemical Design of Solid-State Spin Defects
Defects in semiconductors have become powerful hosts for spin-based qubits in the solid state within materials including diamond, silicon carbide, and silicon (Awschalom et al. 2018). By exploiting defects (Figure 4-2) generated via electron or ion radiation as well as naturally occurring defects in these materials, researchers have
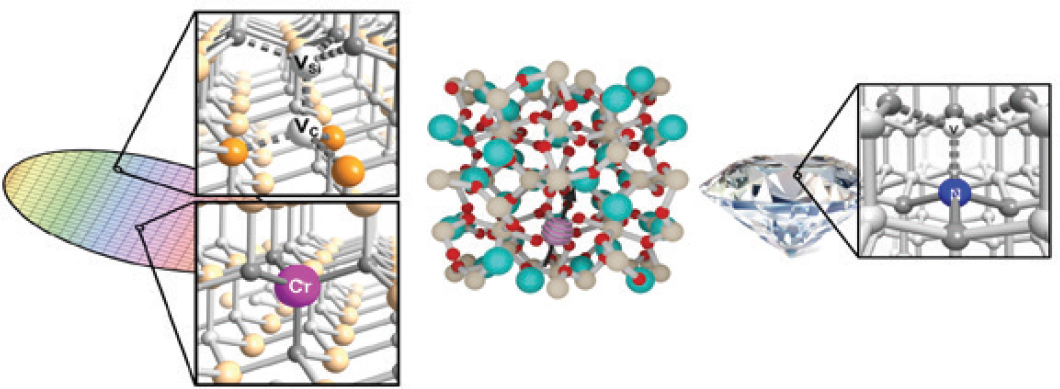
SOURCE: Daniel Laorenza, from the Freedman Laboratory.
demonstrated precise quantum control of individual electron and nuclear spins, robust entanglement, electron–nuclear quantum registers, and increased control of the spin–optical interface at the level of single photons (Anderson et al. 2022). Moreover, driven by predictive theoretical work, several defect-based states have been engineered for practical applications including quantum memories and optical emission (Singh et al. 2022) in the telecommunications regime. Impressive quantum sensing of electric, magnetic, and strain fields has been shown along with dramatic improvements in small-volume and single-spin nuclear magnetic resonance (Morello et al. 2010). However, these material systems face considerable challenges for QIS and engineering, including the creation of scalable and precise quantum states and the mitigation of the impact of strain (Hruszkewycz et al. 2018; Rose et al. 2018), isotopic variations (Balasubramanian et al. 2009; Bourassa et al. 2020), decoherence-driven charge fluctuations from interfaces (Bluvstein et al. 2019; Sangtawesin et al. 2019), and unintentional dopants. Chemistry can play a key role in resolving many of these challenges, especially by exploiting the broad atomic-scale synthesis capabilities for a target qubit, the host matrix, and their mutual interactions. For example, an electron spin qubit interaction with a selected proximal nuclear spin (Graham, Krzyaniak, et al. 2017; Graham, Yu, et al. 2017; Yu et al. 2016) may be optimized through ligand design between weak and strong coupling regimes. In addition, spin-lattice relaxation (Amdur et al. 2022) and the operating temperature of a spin qubit may be engineered by modifying the chemical structure of the ligand and thereby the degree of vibronic coupling at the qubit frequency. Chemistry also provides an opportunity to enhance qubit coherence by controlling the symmetry of the qubit itself or its packing within its host environment (Bayliss et al. 2022; Headley et al. 2016).
The selection of appropriate hosts and defects, and their mutual interactions with one another, remains both a challenge and an opportunity for scientific research. In particular, opportunities that build upon the success of density functional theory (DFT) and coupled cluster expansion techniques in predicting coherent properties of solid-state spin defects (Seo et al. 2017; Weber et al. 2010) may enable the discovery of robust spin qubit candidates. There have been considerable advances in understanding the mechanisms of spin decoherence in semiconductors and solid-state nanostructures (Kanai et al. 2022). State-of-the-art synchrotron spectroscopies, coherent Bragg diffraction imaging, and high-resolution magnetic resonance techniques have proven to be powerful tools to improve the quality of host materials. In addition, improvements in first-principles approaches to understanding and predicting properties (e.g., DFT) have led to a deeper physical understanding of quantum decoherence and successful predictions for mitigating many sources of noise, from dynamical decoupling to unique pulse sequences. Furthermore, there have been successful efforts aimed at harnessing the capabilities of today’s electronic technologies for quantum-state control, including electrical control and readout of single quantum states (Sangtawesin et al. 2019), the creation of decoherence-free subspaces to locally enhance coherence (Miao et al. 2020), and the integration of photonics to both enhance the efficiency of quantum emitters and entangle nearby qubits (Dibos et al. 2018; Lukin, Guidry, and Vučković 2020; Wan et al. 2020). Recently, rare-earth ions in oxide semiconductor hosts—including silicon-compatible materials—have emerged with encouraging properties as single quantum memories, with impressively long coherence times and single-shot photonic readout.
4.2.1c Chemical Design of Superconducting Qubits
Chemistry also offers a potential path toward improving the coherence times of superconducting qubits. While currently one of the most scalable platforms (Arute et al. 2019), superconducting qubits are still plagued with hardware coherence issues that prohibit the realization of fault-tolerant systems (Sheridan et al. 2021; Siddiqi 2021). In superconducting systems (comprising qubits and a resonator), the central hurdle is mitigating decoherence processes that significantly suppress coherence times to well below their theoretical limits. Decoherence processes in superconducting systems currently are dominated by materials-based decoherence through the inevitable inhomogeneities present in multicomponent materials platforms such as defects and interfaces (Krantz et al. 2019). Therefore, reducing materials-based losses in superconducting qubits requires extensive knowledge of the chemical and structural makeup of such complex chemical systems, and predictive routes to their control and mitigation via physical and chemical means. The former requires advanced spectroscopies and microscopies, in tandem with theory, to probe and uncover the structure–property relationships of these heterogeneous nanoscale systems (both their bulk and interfacial properties), often at the forefront of nanoscale characterization. For example, many superconducting qubit systems are made up of amorphous superconductors, for which conventional diffraction
and spectroscopies that rely on reciprocal space cannot be used; novel techniques such as fluctuation electron microscopy (Kennedy et al. 2020) can be used to probe these noncrystalline systems to elucidate information on the bonding environment. Current characterization needs also include nondestructive interfacial probes that can give information on the structure–property relationships of buried interfaces that are often nanometers in extent.
Defect-based decoherence in superconducting qubits is the known Achilles’ heel for superconducting qubits—these comprise primarily parasitic “two-level systems” (TLSs) that are commonly formed at the interfaces between different superconducting components (Martinis et al. 2005). As shown in Figure 4-3, in both Al- and Nb-based superconducting qubits (the most commonly employed materials platforms to date), native oxides form at the interfaces of these elemental systems, resulting in trapped structural configurations that make up the TLS. These metastable chemical configurations can tunnel between equivalent configurations, resulting in an oscillating dipole that electromagnetically couples to the qubit—resulting in decoherence (Phillips 1987). Chemistry can play a unique role in understanding and designing a more favorable chemical environment to reduce, or even eliminate, the chemical motifs associated with TLS noise and other defect-based decoherence. Understanding, reducing, and/or entirely circumventing these parasitic TLSs is a central challenge for developing superconducting circuits. For instance, TLS noise is directly related to the local bonding environment in amorphous suboxides—these suboxides can be passivated with appropriate selective chemical treatment of lossy surfaces (Altoé et al. 2022), and/or modified through doping and/or alloying to reduce the prevalence of the most deleterious TLS by controlling local chemical motifs/coordination (Hamdan, Trinastic, and Cheng 2014). Oxygen off-stoichiometry has been identified as a key cause of parasitic magnetic-based decoherence in Nb oxide thin films (Sheridan et al. 2021), providing a chemical indicator of decoherence in these systems. Another emerging area is the exploration of novel superconducting materials and chemistries as qubits and resonators that are more robust to deleterious TLS formation and/or are comprised of stacked van der Waals bonded two-dimensional (2D) materials, which can circumvent lossy interfaces between dissimilar three-dimensional elements (Altoé et al. 2022).
4.2.1d Chemical Design of Trapped Molecule/Ion Qubits
Ions and molecules that are electromagnetically confined by electromagnetic fields in ultrahigh vacuum are “trapped” ions and molecules. Upon laser-cooling to their motional ground states, they can be used as multiqubit systems (Bollinger et al. 1991). Decoherence for trapped ions is related to both the electric field noise of the laser/trap system and materials-based losses from the electrode surfaces, which are shown to reduce multiqubit

SOURCE: Sinéad M. Griffin.
SOURCE: Brown et al. 2021.
gate fidelities (Brown et al. 2021). Understanding the microscopic origins of these decoherence channels is an ongoing challenge requiring exquisite knowledge and control of the electrode composition—possible sources include vibrations (Wineland et al. 1998), excitations, surface diffusion of chemisorbed atoms/molecules (Kim et al. 2017), and fluctuating “patch charges” on inhomogeneous electrode surfaces (Hite et al. 2013). Current and future challenges for trapped ion/molecule scaling will require surface chemistry approaches (Figure 4-4) to understand lossy electrode surfaces and to design robust, noise-tolerant components and surface treatments that can be cycled for several operations.
4.2.1e Chemical Aspects for the Design of Topological Qubits
While still in their infancy with regard to their demonstrated potential for QIS systems, topological qubits present an exciting possibility for robust, scalable qubits (Kitaev 2003). Owing to its fundamental nature (e.g., the topology of the material), the topological qubit should be inherently robust to certain external perturbations such as defects, strain, and interfaces—in stark contrast to other qubit platforms—and does not require complex error correction. However, while these perturbations often do not destroy the topology of the material, they can make identifying reciprocal-space features extremely difficult by inducing mid-gap states. This, in particular, is the case for both identifying and manipulating Majorana zero modes—the fundamental topological qubit—in physical systems (Nayak et al. 2008). While several routes to achieving Majorana zero modes have been theoretically proposed, no experiments to date have shown definitive evidence of their appearance and braiding (Kayyalha et al. 2020; P. Yu et al. 2021), which motivates materials and chemical approaches to achieving these highly sought-after emergent particles (Figure 4-5; Flensberg, von Oppen, and Stern 2021). Current chemical and materials approaches

SOURCE: Flensberg, von Oppen, and Stern 2021.
to combining strong spin–orbit coupling, superconductivity, and appropriate time-reversal symmetry breaking to achieve Majorana zero modes include semiconductor/superconducting interfaces and molecular/superconducting interfaces (see Figure 4-6). Huge surface chemistry efforts are required to make clean, precisely controlled surfaces with deterministic molecular placement and/or thin nanowires to pass the topological protocol.
4.2.1f Designing Hybrid Quantum Architectures That Mutually Enhance Each Other’s Quantum Properties
Hybrid quantum computers synergistically combine the strengths of classical computing with the opportunities of quantum computing. For instance, a classical optimization algorithm can be used to guide the quantum circuit parameters, while the quantum components solve subtasks more efficiently than would be possible classically.
SOURCE: Nayak 2021.
Further information is detailed below about hybrid quantum–classical algorithms, such as the variational quantum eigensolver (VQE), which have been applied to a range of problems in quantum chemistry. However, for their practical implementation, hybrid quantum computers must additionally combine the hardware requirements of quantum computers (i.e., scalability, coherence, and low error rates) with traditional classical computing components. This will require efficient and low-loss integration of qubit systems with conventional semiconductor technologies such as complementary metal-oxide semiconductor circuits.
4.2.2 Developing Noise Models and Quantum Error-Mitigation Techniques for Individual Qubits, Systems of Qubits, and Quantum Architectures That Can Be Experimentally Validated
No physical system is able to store and operate on information perfectly without errors. Indeed, one of the biggest challenges for quantum information protocols is protection from noise. Error-mitigation techniques that reduce noise thus have to be applied to qubits just as they are routinely applied to classical bits. In contrast to error-correction strategies, error-mitigation strategies involve developing noise models and do not necessitate making and manipulating copies of qubit information, which often makes them more practical in the context of chemistry. Such techniques could accelerate the adoption of moderately imperfect qubits and may enable the use of larger arrays of qubits at the same error rates as smaller arrays without correction, paving the way to larger, multiqubit technologies (Kandala et al. 2019).
But, to apply error-mitigation techniques, detailed models of qubit errors that depend upon the details of the specific qubit technology must be developed. If error models are known, they can be used to analytically reduce errors. Often the origin of this noise stems from molecular processes, meaning that first principles of computational modeling can play a key role in determining the source of the noise and analyzing its form to perform corrections. For example, substantial research has been conducted on quantitatively developing error models for superconducting qubits (Burnett et al. 2019) and ion traps (Foulon et al. 2022) based on the theory of TLSs. Research points to chemical defects at the surface of the oxide and other materials that make up superconducting qubits (Altoé et al. 2022) and the presence of adsorbates on the surface of the electrodes of a trapped-ion quantum computer as leading to anomalous 1/f noise that causes related qubits to decohere rapidly (Bruno et al. 2015; Foulon et al. 2022; Noel et al. 2019; Sedlacek et al. 2018; Wang et al. 2015). First-principles computational simulations of the chemistry at these surfaces enable one to predict how this noise varies based on defect and adsorbate concentrations, adsorbate type, temperature, and frequency, thus yielding models that can be applied directly to measurements to reduce noise and related errors (Aliferis and Preskill 2008; Georgopoulos, Emary, and Zuliani 2021; Tuckett, Bartlett, and Flammia 2018).
Similar models could be developed for molecular qubits. Simple proof-of-principle quantum algorithms for quantum error mitigation have been demonstrated in nuclear spin-based qubits (qudits), where qudits are d-dimensional (d > 2) quantum systems. Molecular strategies for this typically involve single-ion magnets, in which the electron and nuclear spin states are weakly anisotropic or exchange-coupled, leading to multiple spin states that are low in energy. For suitably engineered systems, unequal energy spacings allow addressing via microwave-resonant pulses (Aguilà, Roubeau, and Aromí 2021; Chicco et al. 2021; Gimeno et al. 2021; Hussain et al. 2018; Jenkins et al. 2017; Luis et al. 2011; Moreno-Pineda et al. 2017, 2018). Molecular electron–nuclear spin-based qudits (Ferrando-Soria et al. 2016; Godfrin et al. 2017; Luis et al. 2020) have been utilized for the implementation of quantum mitigation codes, where the molecular systems function as noisy intermediate-scale quantum (NISQ) units (Chiesa et al. 2020, 2021; Macaluso et al. 2020) and the electronic structure is “protected from decoherence.” Taking advantage of nuclear spin structures with greater than two quantum levels (d > 2) in qudits leads to the possibility for long coherence times, due to isolation of the system from the environment, but, consequently, long manipulation times. Strategies to shorten the manipulation times for gate operations involve taking advantage of electron–nuclear coupling (hyperfine interactions) to perform operations on nuclear spin states at rates much shorter than the decoherence times (Castro et al. 2022; Chizzini et al. 2022; Hussain et al. 2018). A combination of further experiments and theory will be necessary to realize these nascent error-mitigation strategies (Castro et al. 2022; Chizzini et al. 2022; Hussain et al. 2018). One should distinguish important problems related to calculating excited-state energies from more formidable challenges of calculating entanglement or coherence in molecules with similar approaches. While the committee realizes that both are very important to chemical understanding, the calculations and approaches should specify the problems to be solved and the potential outcomes initially.
4.2.3 Understanding and Advancing the Limits of Classical Electronic Structure Algorithms and Modeling Approaches That Can Guide the Design of Molecular or Solid-State Qubits and Scalable Quantum Architectures
A promising route to investigating and ultimately designing scalable quantum information platforms is via both classical and quantum computational simulation techniques. Over the past few decades, bolstered by exponential increases in computational power, the simulation of quantum systems on classical computers, including molecules and materials, has evolved from the modeling of approximate coarse-grained systems to provide basic physical insights to the fully ab initio simulation of real and complex materials that can provide predictions that can be compared directly with experiments. Accordingly, many classical computational methods now exist, including DFT, coupled cluster theory (CC; Bartlett and Musiał 2007), and quantum Monte Carlo (QMC) methods (Foulkes et al. 2001), that can now model relatively large quantum systems with both speed and accuracy (Box 4-1). Where systems are too large or complex to be modeled directly using these methods, reasonably accurate and efficient quantum embedding schemes (Huang, Pavone, and Carter 2011; Sun and Chan 2016) that model critical aspects of systems using highly accurate quantum mechanics or less accurate quantum or classical methods have been developed. Indeed, simulation is now viewed as the third pillar of scientific discovery; just as it has been leveraged to provide key insights into the design of catalysts and the identification of potential pharmaceuticals, it now also has the potential to provide invaluable predictions regarding how qubits decohere and how they can be scaled into larger, multiqubit platforms (Lordi and Nichol 2021; Philbin and Narang 2021). For instance, quantum simulations performed on classical computers have recently been leveraged to characterize T-center qubits in Si (Dhaliah et al. 2022) and neutral group IV spin qubit vacancies in diamond (Ma et al. 2020). Nonetheless, several key challenges curtail the straightforward simulation of systems employed for QIS applications and quantum sensors on classical resources.
The rapid advancement of supercomputing power, in tandem with the development of increasingly sophisticated and predictive computational modeling, has made computational and theoretical modeling indispensable for QIS. Such in silico investigations have the advantage of systematically isolating and identifying qubit interactions toward control and design—for instance, accurate modeling of qubit–environment interactions such as qubit–phonon interactions.
4.2.3a Challenges for Modeling Quantum Systems with Classical Resources
As famously noted by Richard P. Feynman in his Lectures on Computation (Feynman, Hey, and Allen 1998), accurately modeling quantum systems on classical computers is a fundamentally expensive task because the number of states a quantum system can potentially occupy grows exponentially with the size of a system. While not all states are equally important and often approximations based on the locality of processes can be made, this scaling inherently limits the ultimate size of quantum systems that can be modeled using quantum resources. As a rule of thumb subject to change in the coming years, tens of isolated atoms can be modeled with high accuracy, while thousands of isolated atoms can be modeled with reasonable accuracy. Incorporating the effects of the environment, as a way to model decoherence, inevitably reduces these numbers even further (Friesner 2005). Moreover, many systems being considered for QIS are definitively strongly correlated and entangled, which means that high-accuracy methods must be employed to uncover useful design principles. Developing new techniques that can exploit physical insights to cheaply yet accurately model quantum information systems thus remains both a challenge and an opportunity for the community. Potential ways of addressing this challenge include the use of physically inspired embedding techniques, new ways of more directly and efficiently computing entanglement and modeling decoherence, the curation and more active use of QIS materials databases, and the employment of increasingly available quantum computing resources.
4.2.3b Modeling Large-Scale Systems Requires Advanced Sampling and Embedding
As previously described, many quantum sensors and quantum information platforms are highly complex, often hybrid materials that integrate qubits into an optimized host environment. The inherently large size of these
systems combined with the typical desire to understand the decoherence processes involving many electronic and phononic degrees of freedom at play in these materials makes directly determining their electronic structure a formidable challenge (Philbin and Narang 2021). While algorithmic advances, including linear scaling and tensor contraction techniques (Hohenstein, Parrish, and Martínez 2012), continue to be made that accelerate the direct modeling of these systems, scaling challenges are often mitigated by different forms of divide-and-conquer techniques: methods that divide the system into smaller portions, which can be modeled with highly accurate theories that can either be stitched back together to recreate the electronic structure of the entire system (Pruitt et al. 2014) or integrated into lower-accuracy descriptions of larger portions of the system.
One of the most productive divide-and-conquer strategies for qubits is embedding (Huang, Pavone, and Carter 2011; Sun and Chan 2016). In embedding theories, a smaller portion of a system that necessitates high-accuracy quantum simulations using techniques such as multireference perturbation theories (Shavitt and Bartlett 2009), CC (Shavitt and Bartlett 2009), QMC (Foulkes et al. 2001), or configuration interaction (Szabo and Ostlund 1989) is modeled surrounded by a larger portion of the system that is treated using lower-accuracy quantum or classical methods. In the context of quantum information systems, the atoms, vacancies, or complexes that constitute the system’s physical qubits are typically modeled with high accuracy, while their hosts are modeled with lower accuracy.
In regard to the various theoretical mechanisms for coupling defect center–based spin qubits to other qubit platforms, potential interface coupling mechanisms such as superconducting qubits, other defect centers, and photons were discussed Wang and colleagues (2021) and are graphically illustrated in Figure 4-7. For the case of gigahertz platforms, dipole-, phonon-, and magnon-mediated mechanisms have been demonstrated. In the case of a dipole-mediated process, challenges remain in the selectivity of the interface mechanism due to the requirement for strict distance and orientation dependence between qubits. While the cavity phonon–mediated dipole coupling may overcome these limitations, other limiting factors present further challenges for the cavity-phonon mechanism. For example, in this mechanism, dipole selection rules limit the use of certain qubit states. Also, further

SOURCE: Wang, Haas, and Narang 2021.
investigation could be undertaken to determine the usefulness of this mechanism, as there may be limitations in the ability to tune two qubits, on demand into resonance for fast entanglement. Another solid-state interface coupling mechanism is that of phonon-mediated quantum interfaces. This approach seems to have the potential to couple qubits over arbitrary distances as long as the qubit states exhibit strain susceptibility. Wang and colleagues (2021) suggest further investigation and development at the nanoscale regarding the systems engineering of the cavity, the materials used, as well as a deeper understanding of the phonon-mediated mechanism. Finally, a more recent approach utilizes a magnon-mediated interaction to effectively couple defect center–based spin qubits with other qubits. This approach offers an enhanced coupling rate in comparison to phonon-mediated interactions. Wang and colleagues (2021) stressed that nanomagnonic systems offer a unique opportunity for nanotechnologists and may have a significant impact on quantum device innovation and translation.
An alternative divide-and-conquer approach to modeling, particularly disordered quantum systems, is through sampling. Disorder is a leading cause of decoherence in many materials and thin films of use in QIS applications (Foulon et al. 2022; Harrelson et al. 2021; Ray et al. 2019). For example, in recent work, researchers studied decoherence in superconducting Nb thin films by sampling over forms of disorder (Harrelson et al. 2021; Sheridan et al. 2021). In sampling techniques, different portions of a typically heterogeneous material are randomly selected to represent the whole, are modeled using high-accuracy methods, and then are averaged to recreate the electronic structure of the larger system. The sampling can be performed according to a uniform distribution or, if information is known about the system, to a more complicated distribution through importance sampling. Alternatively, samples can be generated from snapshots of molecular dynamics simulations or replica exchange Monte Carlo simulations (Frenkel and Smit 2002). Even more recently, experimental data have been used to train machine learning models to learn forms of disorder present over length scales not easily attainable within simulations (Kilgour and Simine 2022). Given sufficient experimental data on surfaces, this presents a promising path forward while emphasizing the need for more detailed experimental characterization of quantum materials for quantum information.
These strategies are but a few of many possible strategies for capturing the complexity of quantum information systems without invoking descriptions that may be more expensive or detailed than necessary. Given these techniques’ inherent approximations, continued research could determine their accuracy, further improve their efficiency, and understand for which materials and properties they perform best. Properly modeling decoherence will moreover necessitate increased exploration into the most efficient ways to integrate descriptions of phonons and electromagnetism into the ab initio modeling of molecules and materials (Philbin and Narang 2021). The committee concludes that the computational modeling of large, heterogenous systems can be accelerated via embedding and sampling approaches on classical systems. Currently, the suite of embedding and other reduced-scaling techniques is underdeveloped. Improving these tools will ultimately lead to a deeper understanding of QIS challenges.
4.2.3c Theoretical and Computational Approaches for Modeling Entanglement
Even if scaling hurdles to simulating large quantum systems on a classical computer can be surmounted, quantifying entanglement and coherence in these systems remains a costly proposition because calculating these quantities requires an accurate accounting of multielectron interactions—often in the presence of phonons and other non-electronic interactions, and usually within a time-dependent framework.
In recent years, several new modeling techniques have emerged for computing entanglement (typically in terms of nth-order Rényi entanglement entropies) in interacting systems, including density matrix renormalization group (DMRG), tensor network, and QMC techniques. Nonetheless, these techniques scale steeply as high-polynomial powers with the size and number of electrons in the system. Even within these frameworks, the computation of the entanglement itself necessitates more time-consuming algorithms than the computation of more traditional quantities like energies and charge densities. To mitigate these steep scalings, attention has turned toward using embedding algorithms, which partition a system into a region that is treated with near-exact levels of theory and a surrounding region that is treated with less accuracy. In the context of quantum information, high-accuracy regions may, for example, be placed around transition metal or lanthanide atoms that host different spin states, while surrounding organic groups may be treated with lower levels of theory. Such embedding methods, including DFT-based embeddings, dynamical mean field theory, and density matrix embedding theory, enable only the
most physically/chemically important regions of a system to be treated, thus substantially reducing the expense of quantum calculations at the cost of modest approximations. In their original forms, these methods were overwhelmingly developed to treat electrons alone. In part inspired by QIS needs, more recent investigations have begun to incorporate phonons/vibrations (Sandhoefer and Chan 2016) into these treatments because of the important role that they assume in decoherence (Sheng et al. 2022). In sum, the committee concludes that computational or theoretical tools for modeling the entanglement and coherence within quantum information processors remain costly. The high cost to use classical computational tools for modeling quantum phenomena is inhibiting key research activities such as direct simulation of large quantum information processors.
4.2.3d Validating the Modeling of Quantum Information Systems
The synergy between experiment and theory can help uncover the molecular and electronic structure that can further develop and improve qubits. As simulations become capable of accurately determining essential properties such as T1 and T2 relaxation times (Ariciu et al. 2019) and the optical response in optically addressable qubits (Goh, Pandharkar, and Gagliardi 2022), models will continue to play an important role in understanding and predicting the feasibility of using a system in a QIS application. Validating computational models is often hindered by the lack of experiments on systematically altered systems. Graham, Yu, and colleagues (2017) demonstrated the power of systematic modifications to vanadyl complexes with increasing distance between vanadium(IV) and a propyl moiety that demonstrates the effect on decoherence as a function of nuclear and electronic spin distance. The growing infrastructure of automated and robotic systems (Seifrid et al. 2022) that synthesize and analyze holds great promise in generating both systematically modified systems and data that can hasten validations.
4.2.3e Leveraging and Developing Machine Learning, Chemical Informatics, Chemical Databases, Molecular Simulations, and Quantum Computing Algorithms to Inform and Facilitate Qubit Design
Materials-informatics approaches are used broadly across the fields of chemistry, materials science, and physics to accelerate the discovery of novel materials and molecules. The explosion of computing power over the past two decades along with improvements in theoretical and computational approaches enable predictive calculations of many compounds, which can be collected into databases. The Materials Genome Initiative kickstarted the foundation of several materials databases with properties predicted from first-principles calculations with a range of applications and properties targeted. For instance, the Materials Project was originally developed for the discovery of battery materials but has expanded to have success across a range of applications including novel photovoltaics, multiferroics, and topological materials. It has recently been extended into the molecular space to include an MOF database (Rosen et al. 2021, 2022). Equivalent databases are starting to become available for molecular compounds (Organic Materials Database) and more complex systems (Automated Interactive Infrastructure and Database for Computational Science and Materials Cloud Two-dimensional Crystals Database).
The use of such materials and cheminformatics approaches for QIS applications is in its infancy yet presents an enormous opportunity to accelerate both the discovery of novel qubits and the understanding of their control in a systematic fashion. High-throughput searches have predicted new topological materials (Frey et al. 2020), and “low-throughput” calculations have been used to identify new spin defects in hexagonal boron nitride (Bhang et al. 2021). First-principles approaches such as these were used to search large combinations of possible defects in Si for new spin defect qubit candidates, with the resulting 400 combinations available in the Quantum Defects Genome database (Xiong et al. 2023). The first-principles approach includes careful benchmarking of the theoretical approaches with experimental measurements, which will improve the predictive power of such approaches. These tools can enable discovery through the exploration of compounds that are synthesizable and have yet to be tested for potential use in QIS technologies (Lilienfeld, Müller, and Tkatchenko 2020). Cheminformatics and machine learning have also been used to determine synthesis routes and to improve synthesis conditions through, for example, the design of experiments methodology (Weissman and Anderson 2015). Keeping the databases fully open and available would advance the field quickly.
4.2.4 Open, High-Quality QIS Software and Data Repositories
As demonstrated in this chapter, theory and computer models play an important role in the advancement of chemistry in the QIS field. Open-source and commercially available electronic structure codes have played an integral role in studying and understanding spectroscopic results in recent studies. The number of codes and applications is extensive, and attempts have been made to track more established software packages. Two examples are referenced here; however, other lists with additional detail may be available (Giannozzi et al. 2009; Scientific Library n.d.). Open-source code enables researchers to replicate and analyze each other’s predictions and build upon past theoretical achievements and code bases instead of having to perennially reinvent the wheel. This accelerates the overall pace of scientific discovery. Moreover, open-source code democratizes discovery by granting researchers who do not have the staff, bandwidth, or expertise to maintain their own codes—including experimentalists who may wish to validate their own results—to still make valuable contributions to the field. Alternatively, commercial software is often more user-friendly, well documented, and regularly updated. Thus, commercial software can be the more favorable option.
However, often free code is not well documented, is difficult to install and use, and ultimately remains inaccessible to many. Software development faces a challenge in striking a balance between ease of human readability and performance-driven computer readability. A set of minimal requirements for open-source code would increase the longevity and transferability of software developed for research and minimize the replication of software tools.
These challenges are not unique to computational chemistry codes, and the computational science community is continually developing tools (e.g., container technology such as Docker, Singularity, and others; see Docker n.d.) to improve the experience of using code across operating systems and environments. While these tools help the user, programmers also need to be considered; this is particularly important in academic groups, in which users often program or reprogram their own software to suit their specific needs. In an information-gathering meeting, the committee heard from Dr. Arman Zaribafiyan (see Appendix B), from Good Chemistry, who highlighted that although the tasks of software engineers and scientists in industry are often clearly delineated, integrated collaboration between the two disciplines is often necessary to solve grand challenges like those posed by the field of QIS. QIS-specific software packages have yet to nucleate, but ensuring that those that eventually rise to the fore remain open will be important for enabling rapid advances.
Equally valuable to the community are the products not only of software but of experiments—that is, data. As described earlier, other communities, including the materials community, have started to develop databases that can be leveraged to guide discovery (Box 4-2). As QIS-specific databases begin to emerge, ensuring that they remain open for widespread exploration will be important. In the case of QIS applications, both theoretical and experimental data, including calculations of decoherence times and entanglement, spectra, and structures, are invaluable not only for validating one another but for facilitating mutual method development. Some of these QIS-relevant data can be harvested from other existing molecular and materials databases, and such efforts to aggregate data have to be undertaken and supported. However, the amount of QIS-specific data is only expected to grow, and the community will need to establish well-structured databases with clear guidelines in the near future. FAIR—Findability, Accessibility, Interoperability, and Reusability—standards (GO FAIR 2017) that emphasize proper labeling for and reusability of data should serve as baselines and be applied wherever possible to ensure professional data management and stewardship.
However, certain challenges associated with intellectual property and proprietary/commercial data need to be carefully balanced to maximize their utility across different sectors while considering the needs of the data sponsors and originators. While public funders’ data should be accessible and follow the FAIR guidelines, data originators may be at a disadvantage if immediate sharing is required. To address this issue, first the community can draw inspiration from other communities with rich data infrastructures. For example, the National Aeronautics and Space Administration allows a data embargo period of one year for scientists who proposed and led the data collection to have time to analyze and publish. Second, it is essential to incorporate robust attribution frameworks and guidelines into all databases so that those who contributed to the data and infrastructure are adequately acknowledged and cited. Finally, incentivizing industry to share their potentially valuable data openly continues to be a challenge that can be overcome through collaboration between open repositories and industry.
4.3 MODELING CHEMISTRY PROBLEMS USING QUANTUM COMPUTERS
Up to this point, the discussions have focused on the current challenges of and progress made with classical computational tools to study complex quantum systems (e.g., qubits) and large molecules. Even with the advancement made, classical computation still faces severe limitations (e.g., computing power and cost) in providing accurate theoretical models for understanding chemical systems employed in QIS applications. Currently, quantum computers face similar challenges to their classical counterparts. Small data input/output, large compute, and super-quadratic speedup of quantum algorithms are three main criteria to determine whether a quantum application can reach a reasonable crossover time and crossover size compared to its classical rival. Although still in the early stages of development, a mature quantum computer may eventually offer an alternative approach for providing enhanced computational tools that surpass the limitations of classical systems. The remainder of this chapter discusses the current challenges and future opportunities in using quantum computers to study chemistry problems that are, at this time, considered extremely difficult to simulate using classical algorithms.
4.3.1 Identifying Important Open Chemistry Problems for Quantum Computers That Are Unresolved Due to Classically Intractable Electronic Structure
While advancements are being made in developing the hardware for quantum computers, many challenges associated with adopting this technology remain (Argüello-Luengo et al. 2019) to gain truly valuable, and classically intractable, insights about chemistry. The first challenge, as demonstrated in this chapter, is that classical computers actually do work quite well for resolving many chemical problems in part because much of chemistry occurs around low-energy electronic states. Such states have limited and structured entanglement, enabling classically efficient methods like DFT to work well often despite making fundamentally uncontrolled approximations. Classically
computable methods are especially viable when the calculations do not require high accuracy and when systems are not “strongly correlated.” A strong correlation (high entanglement) of electrons tends to occur near bond-breaking transitions, in free radicals, and around transition metal centers. Much work remains in understanding how and for what problems quantum computers might provide otherwise inaccessible new chemical insights. First, even if one has an oracle for efficient and completely accurate energy calculations, this does not immediately resolve all chemically relevant questions. An insightful chemist is needed to interrogate the quantum computer thoughtfully to derive a chemical understanding. Second, quantum computers might scale polynomially, but that does not mean the calculations are free (or even as efficient as DFT); indeed, the simulation of chemical Hamiltonians still takes considerable quantum computing resources. Thus, currently, we remain limited in how many electrons can be explicitly treated on a quantum computer; we will need improved methods of embedding the most strongly correlated subsystems inside quantum computations, with the environment treated at lower levels of theory on classical computers.
Finally, as classical methods continue to improve, we face the prospect that the “truly hard” chemistry problems that require a quantum computer will become increasingly esoteric. The problem does not lie in the class of nondeterministic polynomial time (NP) but rather the challenge lies in the fact that the proposed problems cannot be verified efficiently by a classical witness. A generalization of this challenge is Quantum Merlin Arthur (QMA)Hard, which is the quantum version of the class NP; thus, any problem in NP could be solved in polynomial time. This generalization implies that some quantum chemistry problems exist, although of unknown measure, that would be inefficient to solve even on a quantum computer. However, it is still unclear if natural molecular or material Hamiltonians exist that are expected to be found in their ground states in nature that would qualify as QMA-Hard. If that is the case, questions arise about how those systems get into their ground states since any quantum dynamics can be efficiently simulated by a quantum computer (Schuch and Verstraete 2009). Furthermore, see Goings and colleagues (2022) for a case study proposing a target that would be appropriate for a quantum computer and benchmarking the best classical methods against the projected quantum costs. The following section discusses how various chemistry research problems could be vetted to determine their viability for quantum computing applications.
4.3.1a Evaluation of Chemistry Use Cases with Quantum Computers
Below is a set of criteria that could be used to evaluate research proposals that identify chemistry problems that could be addressed using a quantum computer:
- The challenges the investigator is aiming to study need either to have significant scientific merit or industrial relevance or to address a fundamental chemistry question.
- An explanation for why these quantities cannot be obtained using classical methods needs to be provided.
- A compilation is involved of the proposed quantum algorithm to an error-corrected instruction set that is compatible with a scalable, fault-tolerant error-correcting code such as the surface code.
- Estimation of computing time and resources of the best classical methods are included in the proposal. Any research will benchmark these more precisely.
- The proposed work aims to answer the following question: what quantities are being measured and to what precision?
These investigations will serve as case studies that clearly target quantum computing efforts and their role in facilitating our understanding of chemistry. Given the complexity involved between ongoing developments of the quantum computer’s architecture and the need to have appropriate chemical problems to study with these new technologies, the committee has provided Recommendation 4-2, summarized at the end of the chapter.
4.3.2 Studying How Quantum Computing Algorithms for Dynamics Can Be Used to Accelerate Chemistry and Spectroscopy
The most promising problems to solve on quantum computers are electronic structures, which can have exponential computational complexity and for which there are several known quantum algorithms to provide exponential speedup. Electronic structure is the foundation for understanding chemical properties and reactivities. For
example, electronic structure calculations have been used often to help assign peaks for complicated experimental spectroscopy; the molecular orbitals from electronic structure calculations are often used to predict and interpret the reactivity of chemical species.
Although challenges are evident, one of the most significant promises of quantum computing is that it can provide exponential speedup for a certain class of problems. The electronic structure problem is the problem of solving for the ground state of electrons interacting with each other through the Coulomb potential and with the point charges arising from the nuclei. Such ground states characterize the electronic wave functions of molecular systems and materials.
Subspace full configuration interaction (FCI) is not commonly used in routine chemistry applications due to the very restricted size (small molecules) of the affordable one-particle basis and because reliable relative energies may not require ultimate accuracy of total energies (Liu et al. 2022). In the spirit of FCI, many lower-scaling algorithms have been developed for chemistry applications. These traditional algorithms represent the state of the art for solving the electronic Schrödinger equation with high accuracy (Eriksen et al. 2020; Motta et al. 2017; Williams et al. 2020). The core idea is still to solve the eigenvalue problem either by using predefined restrictions of the many-electron basis (coupled cluster with a full treatment of singles and doubles (CCSD(T)), or Davidson correction (MRCI+Q)) or through an iterative construction of the basis-set expansion (DMRG, FCIQMC). The restriction to a selected finite set of active orbitals in all FCI-type approaches generates an artificial distinction of electronic correlations into two groups: (1) static electronic correlations, which are typically characterized by orbitals that occur in determinants with large weight in the wave function expansion; and (2) dynamical electronic correlations, which refers to orbitals present in determinants with small to vanishing weights. This artificial split into static and dynamical electronic correlations can be overcome if a routine numerical approach is used to obtain results of FCI quality on a one-particle basis of one to a few thousand orbitals. There are several FCI-type approaches to address static and dynamical electronic correlations. Even though it is difficult to rigorously assess the error in the energy after a fixed number of optimization cycles with predefined parameters, these traditional methods likely will remain the reference methods for most quantum chemistry calculations, at least in the near term.
Certain critical chemical problems and processes have electronic structures that are too complicated to be handled by any classical methods. FeMo cofactor (FeMoCo) of the nitrogenase enzyme responsible for nitrogen fixation has been discussed frequently and likely represents the most complicated electronic structure (Lee et al. 2021; Li et al. 2019; Reiher et al. 2017). Metalloporphyrin, which often plays an important role in biological processes, is another example of a complex electronic structure (but simpler and more typical than FeMoCo) that supports the need for quantum computers. Even though the active space size in both examples is similar, due to the nature of the electronic structure, the estimated run time on quantum computers is different. Thus, the high-accuracy treatment of strong correlation offered by quantum computers is relevant for understanding mechanisms in inorganic catalysis, for example. Solving the modern electronic structure problem will provide deeper insight into the properties and behaviors of other strongly correlated systems, such as transition metal and heavy metal complexes and biradicals. As demonstrated in Chapter 3 these classes of molecules also have potential utility in a variety of quantum applications. Therefore, gaining more accurate details about the nature of their chemical processes like bond breaking, excited-state transitions, and magnetic properties will be critical for streamlining the development of functional materials. However, to reach high levels of accurate predictions, progress first needs to be made toward solving the modern electronic structure problem.
The committee was presented with expert information regarding the possibility of utilizing quantum computers with new strategies for accurate calculations of highly correlated systems. The committee found that chemistry could play a role in the development of new approaches and algorithms specific to the use of a quantum computer in chemistry. One such idea, of many, involves a method of moments coupled cluster (MMCC) formulism. Some success has been reported on utilizing this method to effectively correct the energies of approximate coupled cluster formulations using moments that are not used to determine approximate cluster amplitudes (Peng and Kowalski 2022). Reports have suggested that particular quantum algorithms for computing MMCC ground-state energies offer a clear advantage over classical computing approaches. While great work remains to be performed to illustrate the robustness of such an approach, this example demonstrates a quantum computing approach that may provide the utility to calculate a strongly correlated system, which was previously thought to be impossible
with classical approaches. This and other approaches on the horizon are important in the development of our understanding of the true advantage of the quantum computing approach. Researchers in this area, in all settings, should be encouraged in their use of new approaches with quantum computers in chemistry that illustrate a strong advantage (McArdle et al. 2020).
4.3.2a Developing More Efficient Methods of Encoding Chemical Systems on Quantum Computers
Calculating total electronic energies with known accuracy is the basis for any theoretical description of molecular systems. As encoding the exact determinant space for large systems having many orbitals (>18) is very challenging on classical hardware, a key goal of all these novel methods is to approximate the full determinant space. Quantum computing holds promise to accomplish this goal, provided that a sufficiently large quantum computer can be built. The most studied approach to solving the electronic structure problem is quantum phase estimation (QPE), which is a fully quantum algorithm that can solve exact solutions of the chemical wave functions and energies. Bayesian phase difference estimation (Sugisaki et al. 2022) and other methods (Arute et al. 2019) are also used; however, the remaining discussion will be focused on QPE. QPE provides an appealing quantum speedup compared to classical rivalries like FCI. For classical computers, as explained in Box 4-1, FCI is a classical algorithm that solves the electronic structure problem; however, it uses exponential scaling.
In QPE, one chooses a trial state, a target error in the eigenvalue estimate, and a desired success probability. The algorithm then returns an estimate of a randomly selected eigenstate. Importantly, the eigenvalue is sampled with some probability. If ground-state energies are desired, then the trial state should be chosen to make the overlap with the true ground state reasonably large. Many ways exist to prepare initial states including using matrix product states, adiabatic-state preparation, and unitary coupled clusters. Different research groups are developing procedures to increase the efficiency of preparing the initial states (Lee et al. 2023). Importantly, if an initial state is difficult to establish, as is the case in strongly correlated systems, then the initial-state overlap will be weak.
There are concerns that sometimes the dependence on the initial-state overlap can lead to poor scaling in the quantum algorithm, especially when the initial overlap is weak (Aspuru-Guzik et al. 2005; Lee et al. 2023). Furthermore, this algorithm measures the eigenvalue of unitary matrices. Quantum circuits can be used to synthesize unitary matrices that share an eigenbasis with the molecular Hamiltonian—for example, via realizing time evolution. Quantum walks are also a popular alternative (Babbush et al. 2018). Developments are under way to increase the efficiencies of these quantum algorithm approaches and lower their costs. Finally, a major setback of using QPE, at the moment, is that it requires quantum hardware that may not be completely accessible in the near future.
4.3.2b VQE to Solve for Electronic Structure
An alternative to a fully quantum algorithm like QPE is VQE. VQE is considered a meta-algorithm, or algorithmic framework, for a quantum–classical hybrid approach where the quantum computer does some work and the classical computer does some work (Chen et al. 2021). VQE is attractive for studying quantum chemistry problems using a popular quantum computer known as the NISQ (McClean et al. 2016).
Running quantum algorithms on real hardware is essential for understanding their strengths and limitations, especially in the NISQ. Simulations assume a perfect system and do not effectively take into account the decoherence errors, loss of accuracy, and time-outs that can occur on real systems (Yamamoto et al. 2022). Quantum computers have evolved from exploratory physics experiments into cloud-accessible hardware as early stage commercial products that are available to a broad audience of chemists and those in other disciplines (Endo, Benjamin, and Li 2018). NISQ-era computers can experience a wide range of complex errors. Many of these errors result from noise in or miscalibrations of the lowest-level components in the system, quantum gate operations, and decoherence in the qubits themselves. The Quantum Economic Development Consortium sponsored a quantum benchmarking project that resulted in an open-source suite of bench tools to run on various quantum hardware systems (Lubinski et al. 2023). This work could be extended to benchmark real chemical structure calculations and molecular energy measurement algorithms on real hardware (Gulka et al. 2021).
VQE is attractive for NISQ because it does not require long coherent circuits like QPE (O’Malley et al. 2016). However, the number of circuit repetitions required is dramatically more for VQE, which can eventually
lead to other challenges such as reaching the limits of NISQ supporting capabilities (Peruzzo et al. 2014; Wecker, Hastings, and Troyer 2015).
The compatibility between VQE and NISQ is exemplified in the simulation of electronic structures, where VQE can be modified or constrained to find the electronic state with a specific number of electrons, electron spin, or other properties (Ryabinkin, Genin, and Izmaylov 2019). Another significant simulation problem addressed by VQE is the dynamic correlated states in a quantum system. The state characterizes the dynamics of quantum particles through the (correlated) system and provides insight into its resulting optical, magnetic, and transport properties. The state also allows access to many static observables, notably the total energy of the system. The ability to understand the dynamic correlated-state system can apply to the understanding of high-temperature semiconductors although the observation will be limited by circuit depth (Chen et al. 2021).
VQE uses the output of a parameterized quantum circuit as an “ansatz” (i.e., a mathematical assumption about the form of an unknown function that is made to find a solution to an equation or other problem) or a trial for the true ground state. The energy of the ground state is calculated using the quantum computer. Then, the classical computer optimizes the parameters of the quantum circuit to lower the energy of the ansatz (Grimsley et al. 2019; Peruzzo et al. 2014).
Furthermore, the committee received expert information from Professor Giulia Galli (see Appendix B), who has made progress in the use of quantum computers for chemical calculations. Galli’s work involves using quantum calculations to predict and design novel molecular and nano-qubits. The long-term goal of the research is to create new simulations on quantum computers for greater accuracy and speed. As illustrated in Figure 4-8, many of the chemistry problems explored using VQE on NISQ are on very simple chemical systems, like diatomic molecules (H2, LiH, NaH, and others), and still require significant error correction to the raw data (see graph in Figure 4-8).
VQE has also been implemented to simulate two intermediate-scale chemistry problems: the binding energy of hydrogen chains, as large as H12, and the isomerization mechanism of diazene (Arute et al. 2020). The simulation was performed using a circuit consisting of 12 qubits and up to 72 qubit gates. However, the authors reiterate the 50-qubit barrier (known as the classically intractable regime), where the key building blocks of the proposed VQE algorithm are potentially scalable to larger systems that cannot be simulated classically (Arute et al. 2020; O’Brien et al. 2022). Many NISQ VQE chemistry experiments have only been 12 qubits, and data suggest that scaling all up to 50 or more qubits to surpass the classically intractable regime will be challenging.
4.3.2c Exploring How Quantum Machine Learning Can Be Used to Accelerate Chemical Research by Processing Quantum Data from Entangled Sensor Arrays or Quantum Simulations of Chemistry
Another widely anticipated application area for quantum computing is machine learning. Quantum machine learning (QML) (Biamonte et al. 2017) consists of two distinct branches: (1) using quantum computers to accelerate classical machine learning as performed by classical computers and (2) using the quantum advantage of quantum computers to construct fully nonclassical quantum neural networks. While quantum computers hold promise for accelerating classical machine learning algorithms, here we instead focus on the potential for quantum computers to analyze data more rapidly. Perhaps the most pressing challenge in the field of QML is to answer the following question: on what types of data sets do we expect QML to provide a quantum advantage? Currently, the compelling answer to this question is that QML is particularly promising for modeling “quantum data” (Huang et al. 2021). Quantum data are data that consist of quantum states rather than classical information. Examples of quantum data include wave function output by quantum simulations as well as data that are obtained from quantum sensors and then transduced to quantum computers. Section 4.2.3a discusses using classical computers to simulate “quantum data”; however, this technique is limited in providing “enough” data due to computational power and cost.
Recent work has shown that when learning from quantum data is applied, it is possible to achieve an exponential advantage in learning. Quantum data can be generated from performing quantum simulations of chemical systems, and learning is applied on top of those data (Huang et al. 2022). This exponential advantage arises because exponentially fewer data are needed if the data are “quantum data” and entangled. Furthermore, because this is a query advantage (i.e., needing less data) as opposed to a conventional quantum speedup (i.e., an algorithm with faster run time), it is possible to reach a quantum advantage with few qubits, especially in the context where data are limited. For example, this advantage could help in understanding topological order in systems, which is a
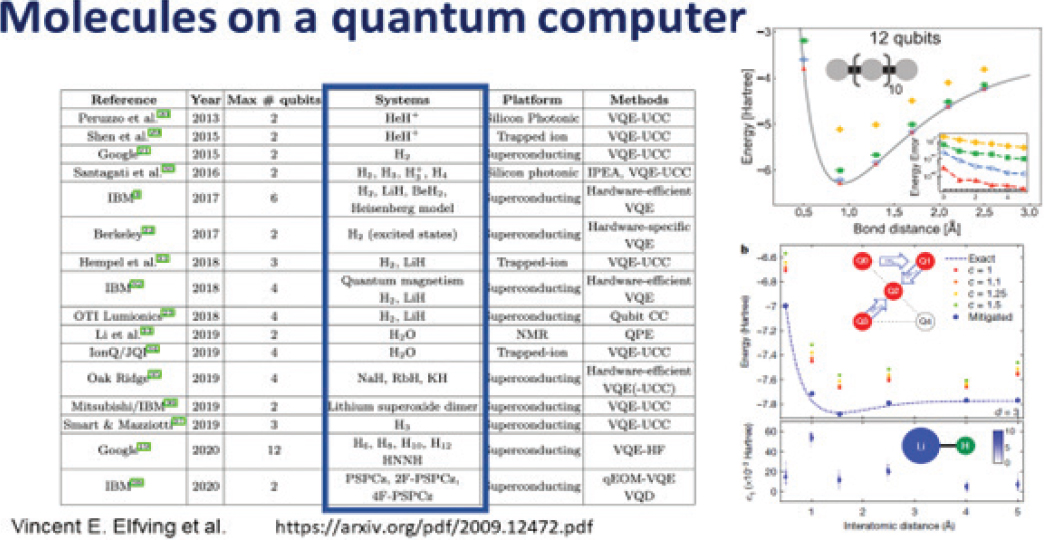
SOURCES: Arute et al. 2020; Elfving et al. 2020; Kandala et al. 2019.
global property of the wave function that cannot be observed by local measurements. Another potential impact of this area on chemistry is that quantum sensors (either molecular sensors or sensors using a different technology), where the state of the sensor can be transduced to a quantum computer, might allow new tools for investigations within a chemical laboratory. This direction has many synergies with molecular sensors and molecular qubits in the context of quantum signal transduction, and both technologies would likely need to be further developed to make this a reality.
4.3.3 Developing More Efficient Quantum Algorithms for Fault-Tolerant Quantum Computers to Simulate Molecular Systems
Quantum simulations, like classical theory, are facing accuracy issues in predicting large molecules. Currently, the most studied model for such systems is medium-sized inorganic catalyst molecules, which are a subject of homogeneous catalysis research. The challenge is to find an application that is insurmountable by current quantum
computers. And, the system is large enough to be predicted accurately with a quantum computer without the need for gross oversimplifications. Because the architecture of quantum computers is still premature, the technology is understandably plagued with defects that ultimately cause data to be highly erroneous. Having an understanding of the basic architecture of quantum computers will help the chemist determine which types of chemistry problems will be suitable for a quantum computer versus a classical computer. Box 4-3 elaborates further on quantum digital gates.
Two major architectures are competing for popular acceptance: fault-tolerant quantum computing (FTQC) and, as described earlier, NISQ. NISQ exists now, and is small scale and non–error corrected. NISQ may use digital or analog paradigms, and current devices are based on both approaches. For FTQC, the digital (gate) approach to error correction for fault tolerance is better developed as a concept, hence the belief that it will be the most likely useful, far-future solution. Whether it would be possible to realize a fault-tolerant analog quantum computer remains unknown.
The ultimate goal for quantum computing systems is to design platforms capable of eliminating the amount and intensity of noise generated in the data, which is directly related to the overall quality of analysis. Two
main approaches have been executed in the development process to address this problem: error correction and error mitigation.
Unlike with classical computers, one cannot simply copy quantum information and use a “repetition code” to correct errors as a consequence of the quantum no-cloning theorem (Wootters and Zurek 1982). Instead, a theory of quantum error correction is now very developed that is based on topology (Kitaev 2006). Topology is a global property of objects. For example, one cannot tell if a donut and a coffee cup are topologically the same or different just by examining a small piece of one of those objects; one must examine the entire object. Hence, topological information is nonlocal. By contrast, errors that occur in individual two-qubit gates or errors that occur from the system interacting with the environment (in most cases) are local. Thus, quantum error correction is based on the idea that if quantum information is encoded in global topological properties of quantum states, it will be robust to errors. A well-developed theory of FTQC now exists.
With FTQC codes, as one increases the number of physical qubits used to store a single “logical qubit,” the error rate decreases exponentially. The most popular error-correcting code that can be made fully fault tolerant (meaning that one can exponentially suppress errors in all aspects of the code, including logical operations, measurements, decoding, and encoding, so long as error rates are “low enough”) is the surface code. The surface code is a topological code (a 2D variant of the Toric code) composed to work for qubits on a planar lattice (Fowler et al. 2012). The surface code is the most popular code because it has the lowest “threshold” of any known code involving only 2D connectivity. 2D connectivity is attractive because devices with higher connectivity pose extreme engineering challenges. The surface code, or close variants like the honeycomb code (Haah and Hastings 2022), is the plan of record for most efforts to build an error-corrected quantum computer, including the leading ion trap, photonics, and superconducting qubit efforts.
The best two-qubit gate fidelities for quantum hardware today that have scaled to more than a few qubits have roughly f = 0.99 (Egan et al. 2021; Google AI n.d.). This value is near the error threshold for the surface code. At those error rates, one would require at least several thousand physical qubits for each logical qubit. Thus, a quantum computer with a few hundred logical qubits would require nearly one million physical qubits. The overheads decrease somewhat if the error rates come down further. For example, with 1e−4 or 1e−5 error rates, the total number of physical qubits for a processor with a few hundred logical qubits might be reduced to closer to 100,000. But it is considered unlikely that error rates as low as 1e−5 will be reached with our current paradigms.
One possibility for getting physical error rates that low is topological quantum computing (Nayak et al. 2008), but so far not even a single topological qubit has been produced. If we were to use a platform with f = 0.999 gate fidelities as a NISQ platform (this would be an extremely accurate NISQ device), then already for L = 1e5 gates (a relatively “small” quantum circuit) the total success probability would be on the order of 4e−5. This means that the quantum computer would need to be run 1/(4e−5) times, or about 20,000 times, just to see a single realization that is not errant. How plausible that is depends on the hardware. Superconducting qubits have gate times on the order of tens of nanoseconds, so this might take only tens of seconds. But ion traps, for example, are several orders of magnitude slower. And it can be very difficult to determine when an error has occurred. Strategies for detecting when errors have occurred so that one can postselect on error-free outcomes, but which do not actually remove the exponential scaling associated with these errors, are referred to as “error mitigation” (which is quite a different topic entirely from “error correction,” despite similar sounding names; see Section 2.2.3 for further details) (Cai et al. 2022).
Most of the time, FTQC algorithms are studied formally. For example, scientists aim to quantify (either asymptotically or in terms of finite resources like constant factors) the number of logical or physical qubits and quantum gates required to perform a precise task. An example of this task is simulating a wave function, starting in its initial state under the molecular Hamiltonian for time (t) and having it evolve within a controlled error (ε). The parameters considered in this system would include the number of particles, number of basis functions, size of particles, and other variables that could affect the behavior of the system.
Work to improve the cost of these algorithms has been ongoing. Su and colleagues (2021) and Lee and colleagues (2021) attempt to show how the cost of quantum algorithms for chemistry in both plane wave and molecular orbital basis sets has improved over the years. Note that while these studies contain very detailed analyses of the costings, the costings are sometimes difficult to compare.
4.3.4 Closing the Loop: Modeling Quantum Information Systems on Quantum Computers
Modeling even the smallest of quantum systems requires classical resources that scale—at best, polynomially, and at worst, exponentially—with system size. On one hand, capturing the size and complexity of realistic quantum information processors and sensors represents a stark challenge for modern classical simulation. On the other hand, this challenge presents a grand and fascinating opportunity for using quantum computers to model future versions of themselves—and other quantum information devices.
Although modern quantum computers are inherently noisy, they have shown substantial speedups in determining the properties and dynamics of a wide array of quantum systems, including popular tight-binding models, small molecules, and simple materials. These speedups can also be extended to the modeling of quantum devices. For instance, by leveraging embedding theories to reduce the size of the quantum problem to be solved, Huang, Govoni, and Galli (2022) and Ma, Govoni, and Galli (2020) recently used quantum computers to model spin defects in semiconductors, including the negatively charged nitrogen-vacancy center, the neutral silicon-vacancy center, and the Cr impurity in 4H-SiC (Vorwerk et al. 2022), which are some of the most popular forms of qubits eyed for future quantum technologies. Quantum simulations using the QPE and VQE algorithms were able to determine the ground and select excited states of the nitrogen-vacancy center within 0.2 eV (Ma, Govoni, and Galli 2020). This demonstration highlights the promise of using quantum computers to inform the design of future quantum computers in a continuous self-improvement loop.
Despite these demonstrations, it remains challenging to fully realize the intricacy of quantum information processors on modern quantum computers. These processors can involve numerous degrees of freedom, which can be difficult to map to most modern machines’ finite numbers of qubits. Even if this mapping can be performed, the solutions to many quantum problems necessitate levels of accuracy that are difficult for quantum computers to achieve given modern levels of noise and tomography costs. More importantly, most quantum sensors and other devices are inherently open systems that exchange energy and other quantities with their environments, necessitating that some aspect of their environments also be represented on limited computing resources. This leaves room for exciting developments that will overcome these challenges and will benefit both current technologies and the future quantum devices they can synergistically advance.
4.4 SUMMARY OF RESEARCH PRIORITIES AND RECOMMENDATIONS
The following fundamental research priorities have been identified by the committee and extensively discussed in Chapter 4 as those that the Department of Energy and the National Science Foundation should prioritize within the target research area of “experimental and computational approaches for scaling qubit design and function.”
Research Priorities:
- Exploit the advantages of bottom-up chemical synthesis for constructing quantum architectures.
- Develop techniques for synthesizing molecular qubits that retain their desirable quantum properties in different host chemical environments.
- Investigate and control the interactions among qubits and between qubits and their environments.
- Design hybrid quantum architectures that mutually enhance each other’s quantum properties.
- Develop noise models and quantum error-mitigation techniques for individual qubits, systems of qubits, and quantum architectures that can be experimentally validated.
- Understand and advance the limits of classical electronic structure algorithms and modeling approaches that can guide the design of molecular or solid-state qubits and scalable quantum architectures.
- Leverage and develop machine learning, chemical informatics, chemical databases, and molecular simulations to inform and facilitate qubit design.
- Identify important open chemistry problems including those with applications to QIS that are unresolved due to classically intractable electronic structure.
- Develop more efficient methods of encoding chemical systems on quantum computers (e.g., better basis sets, quantization, fermion mappings, embedding theories).
- Develop more efficient quantum algorithms for fault-tolerant quantum computers to simulate molecular systems, including those with QIS relevance.
- Study how quantum computing algorithms for dynamics can be used to accelerate chemistry and spectroscopy.
- Explore how quantum machine learning can be used to accelerate chemical research by processing quantum data from entangled sensor arrays or quantum simulations of chemistry.
The committee makes Recommendation 4-1 to address issues concerning open-access databases and the importance of sharing data across relevant research entities to move the field of QIS and chemistry forward. The related discussion included ways to improve the organization and types of relevant experimental and theoretical data that would be useful for the research community. The committee puts forth Recommendation 4-2 to ensure that efforts in QIS research involving quantum-accelerated calculations keep chemistry-related problems at the forefront of the research questions to solve.
Recommendation 4-1. The Department of Energy and the National Science Foundation should establish open-access, centralized databases that include quantum information science (QIS)–relevant data to enhance predictions and expedite new discoveries. These databases should contain (1) structure–property relationships, (2) results of electronic structure calculations, (3) spectroscopic data, (4) experimental characterization of quantum devices, and (5) other data to inform QIS investigations. These data should be obtained from QIS studies contributed by scientists and engineers across industry, academia, and government. These agencies should also create a centralized database to house a body of experimental work that demonstrates discrete quantum use cases for chemistry.
Recommendation 4-2. The Department of Energy, the National Science Foundation, and other funding agencies, both public and private, should develop initiatives to support multidisciplinary research in quantum information science to address how quantum-accelerated calculations could solve chemistry problems. In connection with these initiatives, the research community should establish a set of standards for how to evaluate quantum advantage in specific chemistry use cases.
REFERENCES
Abobeih, M. H., J. Cramer, M. A. Bakker, N. Kalb, M. Markham, D. J. Twitchen, and T. H. Taminiau. 2018. “One-Second Coherence for a Single Electron Spin Coupled to a Multi-Qubit Nuclear-Spin Environment.” Nature Communications 9(1):2552. doi.org/10.1038/S41467-018-04916-Z.
Aguilà, D., O. Roubeau, and G. Aromí. 2021. “Designed Polynuclear Lanthanide Complexes for Quantum Information Processing.” Dalton Transactions 50(35):12045–12057. doi.org/10.1039/D1DT01862K.
Aliferis, P., and J. Preskill. 2008. “Fault-Tolerant Quantum Computation Against Biased Noise.” Physical Review A 78(5):052331. doi.org/10.1103/Physreva.78.052331.
Altoé, M. V. P., A. Banerjee, C. Berk, A. Hajr, A. Schwartzberg, C. Song, M. Alghadeer, S. Aloni, M. J. Elowson, J. M. Kreikebaum, E. K. Wong, S. M. Griffin, S. Rao, A. Weber-Bargioni, A. M. Minor, D. I. Santiago, S. Cabrini, I. Siddiqi, and D. F. Ogletree. 2022. “Localization and Mitigation of Loss in Niobium Superconducting Circuits.” PRX Quantum 3(2):020312. doi.org/10.1103/Prxquantum.3.020312.
Amdur, M. J., K. R. Mullin, M. J. Waters, D. Puggioni, M. K. Wojnar, M. Gu, L. Sun, P. H. Oyala, J. M. Rondinelli, and D. E. Freedman. 2022. “Chemical Control of Spin–Lattice Relaxation to Discover a Room Temperature Molecular Qubit.” Chemical Science 13(23):7034–7045. doi.org/10.1039/D1SC06130E.
Anderson, C. P., E. O. Glen, C. Zeledon, A. Bourassa, Y. Jin, Y. Zhu, C. Vorwerk, A. L. Crook, H. Abe, J. Ul-Hassan, T. Ohshima, N. T. Son, G. Galli, and D. D. Awschalom. 2022. “Five-Second Coherence of a Single Spin with Single-Shot Readout in Silicon Carbide.” Science Advances 8(5):Eabm5912. doi.org/10.1126/Sciadv.Abm5912.
Argüello-Luengo, J., A. González-Tudela, T. Shi, P. Zoller, and J. I. Cirac. 2019. “Analogue Quantum Chemistry Simulation.” Nature 574(7777):215–218. https://doi.org/10.1038/s41586-019-1614-4.
Ariciu, A.-M., D. H. Woen, D. N. Huh, L. E. Nodaraki, A. K. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans, and F. Tuna. 2019. “Engineering Electronic Structure to Prolong Relaxation Times in Molecular Qubits by Minimising Orbital Angular Momentum.” Nature Communications 10(1):3330. doi.org/10.1038/S41467-019-11309-3.
Arute, F., K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. Mcewen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis. 2019. “Quantum Supremacy Using a Programmable Superconducting Processor.” Nature 574(7779):505–510. doi.org/10.1038/S41586-019-1666-5.
Arute, F., K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, S. Boixo, M. Broughton, B. B. Buckley, D. A. Buell, B. Burkett, N. Bushnell, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, S. Demura, A. Dunsworth, E. Farhi, A. Fowler, B. Foxen, C. Gidney, M. Giustina, R. Graff, S. Habegger, M. P. Harrigan, A. Ho, S. Hong, T. Huang, W. J. Huggins, L. Ioffe, S. V. Isakov, E. Jeffrey, Z. Jiang, C. Jones, D. Kafri, K. Kechedzhi, J. Kelly, S. Kim, P. V. Klimov, A. Korotkov, F. Kostritsa, D. Landhuis, P. Laptev, M. Lindmark, E. Lucero, O. Martin, J. M. Martinis, J. R. McClean, M. Mcewen, A. Megrant, X. Mi, M. Mohseni, W. Mruczkiewicz, J. Mutus, O. Naaman, M. Neeley, C. Neill, H. Neven, M. Y. Niu, T. E. O’Brien, E. Ostby, A. Petukhov, H. Putterman, C. Quintana, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, D. Strain, K. J. Sung, M. Szalay, T. Y. Takeshita, A. Vainsencher, T. White, N. Wiebe, Z. J. Yao, P. Yeh, and A. Zalcman. 2020. “Hartree-Fock on a Superconducting Qubit Quantum Computer.” Science 369(6507): 1084–1089. doi.org/10.1126/Science.Abb9811.
Aspuru-Guzik, A., A. D. Dutoi, P. J. Love, and M. Head-Gordon. 2005. “Simulated Quantum Computation of Molecular Energies.” Science 309(5741):1704–1707. doi.org/10.1126/Science.1113479.
Atzori, M., and R. Sessoli. 2019. “The Second Quantum Revolution: Role and Challenges of Molecular Chemistry.” Journal of the American Chemical Society 141(29):11339–11352. doi.org/10.1021/Jacs.9b00984.
Atzori, M., E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace, and R. Sessoli. 2016. “Quantum Coherence Times Enhancement in Vanadium(IV)-Based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety.” Journal of the American Chemical Society 138 (35): 11234–44.
Awschalom, D. D., R. Hanson, J. Wrachtrup, and B. B. Zhou. 2018. “Quantum Technologies with Optically Interfaced Solid-State Spins.” Nature Photonics 12(9):516–527. doi.org/10.1038/S41566-018-0232-2.
Babbush, R., C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler, and H. Neven. 2018. “Encoding Electronic Spectra in Quantum Circuits with Linear T Complexity.” Physical Review X 8(4):041015. doi.org/10.1103/Physrevx.8.041015.
Balasubramanian, G., P. Neumann, D. Twitchen, M. Markham, R. Kolesov, N. Mizuochi, J. Isoya, J. Achard, J. Beck, J. Tissler, V. Jacques, P. R. Hemmer, F. Jelezko, and J. Wrachtrup. 2009. “Ultralong Spin Coherence Time in Isotopically Engineered Diamond.” Nature Materials 8(5):383–387. doi.org/10.1038/nmat2420.
Barends, R., J. Kelly, A. Megrant, A. Veitia, D. Sank, E. Jeffrey, T. C. White, J. Mutus, A. G. Fowler, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, C. Neill, P. O’Malley, P. Roushan, A. Vainsencher, J. Wenner, A. N. Korotkov, A. N. Cleland, and J. M. Martinis. 2014. “Superconducting Quantum Circuits at the Surface Code Threshold for Fault Tolerance.” Nature 508(7497):500–503. doi.org/10.1038/nature13171.
Bartlett, R. J., and M. Musiał. 2007. “Coupled-Cluster Theory in Quantum Chemistry.” Reviews of Modern Physics 79(1): 291–352. doi.org/10.1103/Revmodphys.79.291.
Bayliss, S. L., P. Deb, D. W. Laorenza, M. Onizhuk, G. Galli, D. E. Freedman, and D. D. Awschalom. 2022. “Enhancing Spin Coherence in Optically Addressable Molecular Qubits through Host-Matrix Control.” Physical Review X 12(3):031028. doi.org/10.1103/PhysRevX.12.031028.
Bhang J., H. Ma, D. Yim, G. Galli, and H. Seo. 2021. “First-Principles Predictions of Out-Of-Plane Group IV and V Dimers as High-Symmetry, High-Spin Defects in Hexagonal Boron Nitride.” ACS Applied Materials and Interfaces 13(38): 45768–45777. doi.org/10.1021/acsami.1c16988.
Biamonte, J., P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, and S. Lloyd. 2017. “Quantum Machine Learning.” Nature 549(7671):195–202. doi.org/10.1038/Nature23474.
Bluvstein, D., Z. Zhang, C. A. Mclellan, N. R. Williams, and A. C. Bleszynski Jayich. 2019. “Extending the Quantum Coherence of a Near-Surface Qubit by Coherently Driving the Paramagnetic Surface Environment.” Physical Review Letters 123(14):146804. doi.org/10.1103/Physrevlett.123.146804.
Bollinger, J. J., D. J. Heizen, W. M. Itano, S. L. Gilbert, and D. J. Wineland. 1991. “A 303-MHz Frequency Standard Based on Trapped Be+ Ions.” IEEE Transactions on Instrumentation and Measurement 40(2):126–128. doi.org/10.1109/TIM.1990.1032897.
Bourassa, A., C. P. Anderson, K. C. Miao, M. Onizhuk, H. Ma, A. L. Crook, H. Abe, J. Ul-Hassan, T. Ohshima, N. T. Son, G. Galli, and D. D. Awschalom. 2020. “Entanglement and Control of Single Nuclear Spins in Isotopically Engineered Silicon Carbide.” Nature Materials 19(12):1319–1325. doi.org/10.1038/s41563-020-00802-6.
Brown, K. R., J. Chiaverini, J. M. Sage, and H. Häffner. 2021. “Materials Challenges for Trapped-Ion Quantum Computers.” Nature Reviews Materials 6(10):892–905. doi.org/10.1038/S41578-021-00292-1.
Bruno, A., G. de Lange, S. Asaad, K. L. van der Enden, N. K. Langford, and L. DiCarlo. 2015. “Reducing Intrinsic Loss in Superconducting Resonators by Surface Treatment and Deep Etching of Silicon Substrates.” Applied Physics Letters 106(18):182601. https://doi.org/10.1063/1.4919761.
Bruzewicz, C. D., J. Chiaverini, R. Mcconnell, and J. M. Sage. 2019. “Trapped-Ion Quantum Computing: Progress and Challenges.” Applied Physics Reviews 6(2):021314. doi.org/10.1063/1.5088164.
Buluta, I., and F. Nori. 2009. “Quantum Simulators.” Science 326(5949):108–111. doi.org/10.1126/science.1177838.
Burnett, J.J., A. Bengtsson, M. Scigliuzzo, D. Niepce, M. Kudra, P. Delsing, and J. Bylander. 2019. “Decoherence Benchmarking of Superconducting Qubits.” npj Quantum Information 5:54. doi.org/10.1038/s41534-019-0168-5.
Cai, Z., R. Babbush, S. C. Benjamin, S. Endo, W. J. Huggins, Y. Li, J. R. McClean, and T. E. O’Brien. 2022. “Quantum Error Mitigation.” ArXiv preprint. arXiv:2210.00921.
Castro, A., A. García Carrizo, S. Roca, D. Zueco, and F. Luis. 2022. “Optimal Control of Molecular Spin Qudits.” Physical Review Applied 17(6):064028. doi.org/10.1103/Physrevapplied.17.064028.
Chen, H., M. Nusspickel, J. Tilly, and G. H. Booth. 2021. “Variational Quantum Eigensolver for Dynamic Correlation Functions.” Physical Review A 104(3). https://doi.org/10.1103/physreva.104.032405.
Chicco, S., A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi, R. Sessoli, and S. Carretta. 2021. “Controlled Coherent Dynamics of [VO(TPP)], a Prototype Molecular Nuclear Qudit with an Electronic Ancilla.” Chemical Science 12(36):12046–12055. doi.org/10.1039/D1SC01358K.
Chiesa, A., E. Macaluso, F. Petiziol, S. Wimberger, P. Santini, and S. Carretta. 2020. “Molecular Nanomagnets as Qubits with Embedded Quantum-Error Correction.” Physical Review Letters 11(20):8610–8615. doi.org/10.1021/Acs.Jpclett.0c02213.
Chiesa, A., F. Petiziol, E. Macaluso, S. Wimberger, P. Santini, and S. Carretta. 2021. “Embedded Quantum-Error Correction and Controlled-Phase Gate for Molecular Spin Qubits.” AIP Advances 11(2):025134. doi.org/10.1063/9.0000166.
Chizzini, M., L. Crippa, L. Zaccardi, E. Macaluso, S. Carretta, A. Chiesa, and P. Santini. 2022. “Quantum Error Correction with Molecular Spin Qudits.” Physical Chemistry Chemical Physics 24(34):20030–20039. doi.org/10.1039/D2CP01228F.
Daley, A. J., I. Bloch, C. Kokail, S. Flannigan, N. Pearson, M. Troyer, and P. Zoller. 2022. “Practical Quantum Advantage in Quantum Simulation.” Nature 607(7920):667–676. doi.org/10.1038/s41586-022-04940-6.
Devoret, M. H., A. Wallraff, and J. M. Martinis. 2004. “Superconducting Qubits: A Short Review.” ArXiv. arxiv.org/abs/cond-mat/0411174.
Dhaliah, D., Y. Xiong, A. Sipahigil, S. M. Griffin, and G. Hautier. 2022. “First-Principles Study of the T Center in Silicon.” Physical Review Materials 6(5):L053201. doi.org/10.1103/Physrevmaterials.6.L053201.
Dibos, A. M., M. Raha, C. M. Phenicie, and J. D. Thompson. 2018. “Atomic Source of Single Photons in the Telecom Band.” Physical Review Letters 120(24):243601. doi.org/10.1103/Physrevlett.120.243601.
Docker. n.d. “Telepresence.” 9 May 2023, www.docker.com.
Ebbesen, T. W. 2016. “Hybrid Light–Matter States in a Molecular and Material Science Perspective.” Accounts of Chemical Research 49(11):2403–2412. doi.org/10.1021/Acs.Accounts.6b00295.
Egan, L., D. M. Debroy, C. Noel, A. Risinger, D. Zhu, D. Biswas, M. Newman, M. Li, K. R. Brown, M. Cetina, and C. Monroe. 2021. “Fault-Tolerant Control of an Error-Corrected Qubit.” Nature 598(7880):281–286. doi.org/10.1038/S41586-021-03928-Y.
Elfving, V. E., B. W. Broer, M. Webber, J. Gavartin, M. D. Halls, K. P. Lorton, and A. Bochevarov. 2020. “How will Quantum Computers Provide an Industrially Relevant Computational Advantage in Quantum Chemistry?” ArXiv preprint. arXiv:2009.12472.
Endo, S., S. C. Benjamin, and Y. Li. 2018. “Practical Quantum Error Mitigation for Near-Future Applications.” Physical Review X 8(3):031027. doi:10.1103/PhysRevX.8.031027.
Eriksen, J. J., T. A. Anderson, J. E. Deustua, K. Ghanem, D. Hait, M. R. Hoffmann, S. Lee, D. S. Levine, I. Magoulas, J. Shen, N. M. Tubman, K. B. Whaley, E. Xu, Y. Yao, N. Zhang, A. Alavi, G. K.-L. Chan, M. Head-Gordon, W. Liu, P. Piecuch, S. Sharma, S. L. Ten-No, C. J. Umrigar, and J. Gauss. 2020. “The Ground State Electronic Energy of Benzene.” Physical Review Letters 11(20):8922–8929. doi.org/10.1021/Acs.Jpclett.0c02621.
Fataftah, M., M. D. Krzyaniak, B. Vlaisavljevich, M. R. Wasielewski, J. M. Zadrozny, and D. E. Freedman. 2019. “Metal–Ligand Covalency Enables Room Temperature Molecular Qubit Candidates.” Chemical Science 10(27):6707–14. https://doi.org/10.1039/C9SC00074G.
Ferrando-Soria, J., E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes, and R. E. P. Winpenny. 2016. “A Modular Design of Molecular Qubits to Implement Universal Quantum Gates.” Nature Communications 7(1):11377. doi.org/10.1038/Ncomms11377.
Feynman, R. P., J. Hey, and R. W. Allen. 1998. Feynman Lectures on Computation. Boston: Addison-Wesley Longman.
Flensberg, K., F. von Oppen, and A. Stern. 2021. “Engineered Platforms for Topological Superconductivity and Majorana Zero Modes.” Nature Reviews Materials 6(10):944–958. doi.org/10.1038/S41578-021-00336-6.
Foulkes, W. M. C., L. Mitas, R. J. Needs, and G. Rajagopal. 2001. “Quantum Monte Carlo Simulations of Solids.” Reviews of Modern Physics 73(1):33–83. doi.org/10.1103/Revmodphys.73.33.
Foulon, B. L., K. G. Ray, C.-E. Kim, Y. Liu, B. M. Rubenstein, and V. Lordi. 2022. “1/Ω Electric-Field Noise in Surface Ion Traps from Correlated Adsorbate Dynamics.” Physical Review A 105(1):013107. doi.org/10.1103/Physreva.105.013107.
Fowler, A. G., M. Mariantoni, J. M. Martinis, and A. N. Cleland. 2012. “Surface Codes: Towards Practical Large-Scale Quantum Computation.” Physical Review A 86(3):032324. https://doi.org/10.1103/PhysRevA.86.032324.
Freedman, M., A. Kitaev, M. Larsen, and Z. Wang. 2003. “Topological Quantum Computation.” Bulletin of the American Mathematical Society 40(1):31–38.
Frenkel, D., and B. Smit. 2002. Understanding Molecular Simulation: From Algorithms to Applications, Understanding Molecular Simulation (Second Edition). San Diego: Academic Press.
Frey, N. C., M. K. Horton, J. M. Munro, S. M. Griffin, K. A. Persson, and V. B. Shenoy. 2020. “High-Throughput Search for Magnetic and Topological Order in Transition Metal Oxides.” Science Advances 6(50):Eabd1076. doi.org/10.1126/Sciadv.Abd1076.
Friesner, R. A. 2005. “Ab Initio Quantum Chemistry: Methodology and Applications.” Proceedings of the National Academy of Sciences USA 102(19):6648–6653. doi.org/10.1073/Pnas.0408036102.
Gaita-Ariño, A., F. Luis, S. Hill, and E. Coronado. 2019. “Molecular Spins for Quantum Computation.” Nature Chemistry 11(4):301–309. doi.org/10.1038/S41557-019-0232-Y.
Georgescu, I. 2020. “Trapped Ion Quantum Computing Turns 25.” Nature Reviews Physics 2(6):278–278. doi.org/10.1038/S42254-020-0189-1.
Georgopoulos, K., C. Emary, and P. Zuliani. 2021. “Modeling and Simulating the Noisy Behavior of Near-Term Quantum Computers.” Physical Review A 104(6):062432. doi.org/10.1103/Physreva.104.062432.
Giannozzi, P., S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari, and R. M. Wentzcovitch. 2009. “QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials.” Journal of Physics: Condensed Matter 21(39):395502. doi.org/10.1088/0953-8984/21/39/395502.
Gimeno, I., A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau, and F. Luis. 2021. “Broad-Band Spectroscopy of a Vanadyl Porphyrin: A Model Electronuclear Spin Qudit.” Chemical Science 12(15):5621–5630. doi.org/10.1039/D1SC00564B.
GO FAIR. 2017. “FAIR Principles.” https://www.go-fair.org/fair-principles/.
Godfrin, C., A. Ferhat, R. Ballou, S. Klyatskaya, M. Ruben, W. Wernsdorfer, and F. Balestro. 2017. “Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm.” Physical Review Letters 119(18):187702. doi.org/10.1103/Physrevlett.119.187702.
Goh, T., R. Pandharkar, and L. Gagliardi. 2022. “Multireference Study of Optically Addressable Vanadium-Based Molecular Qubit Candidates.” Journal of Physical Chemistry A 126(36):6329–6335. doi.org/10.1021/acs.jpca.2c04730.
Goings, J. J., A. White, J. Lee, C. S. Tautermann, M. Degroote, C. Gidney, T. Shiozaki, R. Babbush, and N. C. Rubin. 2022. “Reliably Assessing the Electronic Structure of Cytochrome P450 on Today’s Classical Computers and Tomorrow’s Quantum Computers.” Proceedings of the National Academy of Sciences USA 119(38):E2203533119. doi.org/10.1073/Pnas.2203533119.
Google AI. n.d. “Advancing AI for Everyone.” 9 May 2023. https://ai.google/.
Graham, M. J., M. D. Krzyaniak, M. R. Wasielewski, and D. E. Freedman. 2017. “Probing Nuclear Spin Effects on Electronic Spin Coherence Via EPR Measurements of Vanadium(IV) Complexes.” Inorganic Chemistry 56(14):8106–8113. doi.org/10.1021/Acs.Inorgchem.7b00794.
Graham, M. J., C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski, and D. E. Freedman. 2017. “Synthetic Approach to Determine the Effect of Nuclear Spin Distance on Electronic Spin Decoherence.” Journal of the American Chemical Society 139(8):3196–3201. doi.org/10.1021/Jacs.6b13030.
Graham, M. J., J. M. Zadrozny, M. S. Fataftah, and D. E. Freedman. 2017. “Forging Solid-State Qubit Design Principles in a Molecular Furnace.” Chemistry of Materials 29(5):1885–1897. doi.org/10.1021/Acs.Chemmater.6b05433.
Graham, M. J., J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill, and D. E. Freedman. 2014. “Influence of Electronic Spin and Spin–Orbit Coupling on Decoherence in Mononuclear Transition Metal Complexes.” Journal of the American Chemical Society 136(21):7623–7626. doi.org/10.1021/ja5037397.
Grimsley, H. R., S. E. Economou, E. Barnes, and N. J. Mayhall. 2019. “An Adaptive Variational Algorithm for Exact Molecular Simulations on a Quantum Computer.” Nature Communications 10(1):3007. doi.org/10.1038/S41467-019-10988-2.
Gulka, M., D. Wirtitsch, V. Ivády, J. Vodnik, J. Hruby, G. Magchiels, E. Bourgeois, A. Gali, M. Trupke, and M. Nesladek. 2021. “Room-Temperature Control and Electrical Readout of Individual Nitrogen-Vacancy Nuclear Spins.” Nature Communications 12(1):4421. doi:10.1038/s41467-021-24494-x.
Haah, J., and M. B. Hastings. 2022. “Boundaries for the Honeycomb Code.” Quantum 6:693. doi.org/10.22331/q-2022-04-21-693.
Hamdan, R., J. P. Trinastic, and H. P. Cheng. 2014. “Molecular Dynamics Study of the Mechanical Loss in Amorphous Pure and Doped Silica.” Journal of Chemical Physics 141(5):054501. doi.org/10.1063/1.4890958.
Harrelson, T. F., E. Sheridan, E. Kennedy, J. Vinson, A. T. N’Diaye, M. V. P. Altoé, A. Schwartzberg, I. Siddiqi, D. F. Ogletree, M. C. Scott, and S. M. Griffin. 2021. “Elucidating the Local Atomic and Electronic Structure of Amorphous Oxidized Superconducting Niobium Films.” Applied Physics Letters 119(24):244004. doi.org/10.1063/5.0069549.
Headley, M. B., A. Bins, A. Nip, E. W. Roberts, M. R. Looney, A. Gerard, and M. F. Krummel. 2016. “Visualization of Immediate Immune Responses to Pioneer Metastatic Cells in the Lung.” Nature 531(7595):513–517. doi.org/10.1038/nature16985.
Helgaker, T., P. Jørgensen, and J. Olsen. 2000. Molecular Electronic-Structure Theory: Helgaker/Molecular Electronic-Structure Theory. New York: John Wiley and Sons.
Hite, D. A., Y. Colombe, A. C. Wilson, D. T. C. Allcock, D. Leibfried, D. J. Wineland, and D. P. Pappas. 2013. “Surface Science for Improved Ion Traps.” MRS Bulletin 38(10):826–833. doi.org/10.1557/Mrs.2013.207.
Hohenstein, E. G., R. M. Parrish, and T. J. Martínez. 2012. “Tensor Hypercontraction Density Fitting. I. Quartic Scaling Second- and Third-Order Møller-Plesset Perturbation Theory.” Journal of Chemical Physics 137(4):044103. doi.org/10.1063/1.4732310.
Hruszkewycz, S. O., S. Maddali, C. P. Anderson, W. Cha, K. C. Miao, M. J. Highland, A. Ulvestad, D. D. Awschalom, and F. J. Heremans. 2018. “Strain Annealing of SiC Nanoparticles Revealed Through Bragg Coherent Diffraction Imaging for Quantum Technologies.” Physical Review Materials 2(8):086001. doi.org/10.1103/Physrevmaterials.2.086001.
Huang, B., M. Govoni, and G. Galli. 2022. “Simulating the Electronic Structure of Spin Defects on Quantum Computers.” PRX Quantum 3(1):010339. doi.org/10.1103/Prxquantum.3.010339.
Huang, C., M. Pavone, and E. A. Carter. 2011. “Quantum Mechanical Embedding Theory Based on a Unique Embedding Potential.” Journal of Chemical Physics 134(15):154110. doi.org/10.1063/1.3577516.
Huang, H.-Y., M. Broughton, J. Cotler, S. Chen, J. Li, M. Mohseni, H. Neven, R. Babbush, R. Kueng, J. Preskill, and J. R. McClean. 2022. “Quantum Advantage in Learning from Experiments.” Science 376(6598):1182–1186. doi.org/10.1126/Science.Abn7293.
Huang, H.-Y., M. Broughton, M. Mohseni, R. Babbush, S. Boixo, H. Neven, and J. R. McClean. 2021. “Power of Data in Quantum Machine Learning.” Nature Communications 12(1):2631. doi.org/10.1038/S41467-021-22539-9.
Huggins, W. J., B. A. O’Gorman, N. C. Rubin, D. R. Reichmn, R. Babbush, and J. Lee. 2022. “Unbiasing Fermionic Quantum Monte Carlo with a Quantum Computer.” Nature 603:416–420. doi.org/10.1038/s41586-021-04351-z.
Hussain, R., G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. S. Pedersen, R. De Renzi, S. Piligkos, and S. Carretta. 2018. “Coherent Manipulation of a Molecular Ln-Based Nuclear Qudit Coupled to an Electron Qubit.” Journal of the American Chemical Society 140(31):9814–9818. doi.org/10.1021/Jacs.8b05934.
Ishikawa, N., M. Sugita, and W. Wernsdorfer. 2005. “Nuclear Spin Driven Quantum Tunneling of Magnetization in a New Lanthanide Single-Molecule Magnet: Bis(Phthalocyaninato)Holmium Anion.” Journal of the American Chemical Society 127(11):3650–3651. doi.org/10.1021/Ja0428661.
Jackson, C. E., C. Lin, S. H. Johnson, J. Tol, and J. M. Zadrozny. 2019. “Nuclear-Spin-Pattern Control of Electron-Spin Dynamics in a Series of V(IV) Complexes.” Chemical Science 10(36):8447–8454. doi.org/10.1039/C9SC02899D.
Jackson, C. E., I. P. Moseley, R. Martinez, S. Sung, and J. M. Zadrozny. 2021. “A Reaction-Coordinate Perspective of Magnetic Relaxation.” Chemical Society Reviews 50(12):6684–6699. doi.org/10.1039/D1CS00001B.
Jenkins, M. D., Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Ariño, C. Giménez-Saiz, P. J. Alonso, E. Coronado, and F. Luis. 2017. “Coherent Manipulation of Three-Qubit States in a Molecular Single-Ion Magnet.” Physical Review B 95(6):064423. doi.org/10.1103/Physrevb.95.064423.
Johnson, M. W., M. H. S. Amin, S. Gildert, T. Lanting, F. Hamze, N. Dickson, R. Harris, A. J. Berkley, J. Johansson, P. Bunyk, E. M. Chapple, C. Enderud, J. P. Hilton, K. Karimi, E. Ladizinsky, N. Ladizinsky, T. Oh, I. Perminov, C. Rich, M. C. Thom, E. Tolkacheva, C. J. S. Truncik, S. Uchaikin, J. Wang, B. Wilson, and G. Rose. 2011. “Quantum Annealing with Manufactured Spins.” Nature 473(7346):194–198. doi.org/10.1038/nature10012.
Jones, R. O. 2015. “Density Functional Theory: Its Origins, Rise to Prominence, and Future.” Reviews of Modern Physics 87(3):897–923. doi.org/10.1103/RevModPhys.87.897.
Kanai, S., F. J. Heremans, H. Seo, G. Wolfowicz, C. P. Anderson, S. E. Sullivan, M. Onizhuk, G. Galli, D. D. Awschalom, and H. Ohno. 2022. “Generalized Scaling of Spin Qubit Coherence in Over 12,000 Host Materials.” Proceedings of the National Academy of Sciences USA 119(15):E2121808119. doi.org/10.1073/Pnas.2121808119.
Kandala, A., K. Temme, A. D. Córcoles, A. Mezzacapo, J. M. Chow, and J. M. Gambetta. 2019. “Error Mitigation Extends the Computational Reach of a Noisy Quantum Processor.” Nature 567(7749):491–495. doi.org/10.1038/S41586-019-1040-7.
Kayyalha, M., D. Xiao, R. Zhang, J. Shin, J. Jiang, F. Wang, Y.-F. Zhao, R. Xiao, L. Zhang, K. M. Fijalkowski, P. Mandal, M. Winnerlein, C. Gould, Q. Li, L. W. Molenkamp, M. H. W. Chan, N. Samarth, and C.-Z. Chang. 2020. “Absence of Evidence for Chiral Majorana Modes in Quantum Anomalous Hall-Superconductor Devices.” Science 367(6473):64–67. doi.org/10.1126/Science.Aax6361.
Kennedy, E., N. Reynolds, L. R. Dacosta, F. Hellman, C. Ophus, and M. C. Scott. 2020. “Tilted Fluctuation Electron Microscopy.” Applied Physics Letters 117(9):091903. doi.org/10.1063/5.0015532.
Kilgour, M., and L. Simine. 2022. “Inside the Black Box: A Physical Basis for the Effectiveness of Deep Generative Models of Amorphous Materials.” Journal of Computational Physics 452:110885. doi.org/10.1016/J.Jcp.2021.110885.
Kim, E., A. Safavi-Naini, D. A. Hite, K. S. Mckay, D. P. Pappas, P. F. Weck, and H. R. Sadeghpour. 2017. “Electric-Field Noise From Carbon-Adatom Diffusion on a Au(110) Surface: First-Principles Calculations and Experiments.” Physical Review A 95(3):033407. doi.org/10.1103/Physreva.95.033407.
Kitaev, A. Y. 2006. “Fault-Tolerant Quantum Computation by Anyons.” Annals of Physics 303(1):2–30. doi.org/10.1016/S0003-4916(02)00018-0.
Koch, W., and M. C. Holthausen. 2001. A Chemist’s Guide to Density Functional Theory. John Wiley and Sons. www.onlinelibrary.wiley.com/doi/book/10.1002/3527600043.
Krantz, P., M. Kjaergaard, F. Yan, T. P. Orlando, S. Gustavsson, and W. D. Oliver. 2019. “A Quantum Engineer’s Guide to Superconducting Qubits.” Applied Physics Reviews 6(2):021318. doi.org/10.1063/1.5089550.
Kundu, K., J. R. K. White, S. A. Moehring, J. M. Yu, J. W. Ziller, F. Furche, W. J. Evans, and S. Hill. 2022. “A 9.2-GHz Clock Transition in a Lu(II) Molecular Spin Qubit Arising from a 3,467-MHz Hyperfine Interaction.” Nature Chemistry 14(4):392–397. doi.org/10.1038/S41557-022-00894-4.
Lee, J., D. W. Berry, C. Gidney, W. J. Huggins, J. R. McClean, N. Wiebe, and R. Babbush. 2021. “Even More Efficient Quantum Computations of Chemistry Through Tensor Hypercontraction.” PRX Quantum 2(3):030305. doi.org/10.1103/Prxquantum.2.030305.
Lee, S., J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin, and G. K. L. Chan. 2023. “Evaluating the Evidence for Exponential Quantum Advantage in Ground-State Quantum Chemistry.” Nature Communications 14(1). https://doi.org/10.1038/s41467-023-37587-6.
Li, Z., J. Li, N. S. Dattani, C. J. Umrigar, and G. K.-L. Chan. 2019. “The Electronic Complexity of the Ground-State of the FeMo Cofactor of Nitrogenase as Relevant to Quantum Simulations.” Journal of Chemical Physics 150(2):024302. doi.org/10.1063/1.5063376.
Lilienfeld, O. A. V., K. R. Müller, and A. Tkatchenko. 2020. “Exploring Chemical Compound Space with Quantum-Based Machine Learning.” Nature Reviews Chemistry 4(7):347–358. https://doi.org/10.1038/s41570-020-0189-9.
Liu, H., G. H. Low, D. S. Steiger, T. Häner, M. Reher, and M. Troyer. 2022. “Prospects of Quantum Computing for Molecular Sciences.” Materials Theory 6(11). doi.org/10.1186/s41313-021-00039-z.
Lordi, V., and J. M. Nichol. 2021. “Advances and Opportunities in Materials Science for Scalable Quantum Computing.” MRS Bulletin 46(7):589–595. doi.org/10.1557/S43577-021-00133-0.
Lovchinsky, I., A. O. Sushkov, E. Urbach, N. P. De Leon, S. Choi, K. De Greve, R. Evans, R. Gertner, E. Bersin, C. Müller, L. Mcguinness, F. Jelezko, R. L. Walsworth, H. Park, and M. D. Lukin. 2016. “Nuclear Magnetic Resonance Detection and Spectroscopy of Single Proteins Using Quantum Logic.” Science 351(6275):836–841. doi.org/10.1126/Science.Aad8022.
Lubinski, T., S. Johri, P. Varosy, J. Coleman, L. Zhao, J. Necaise, C. H. Baldwin, K. Mayer, and T. Proctor. 2023. “Application-Oriented Performance Benchmarks for Quantum Computing.” IEEE Transactions on Quantum Engineering 4:1–32. https://doi.org/10.1109/tqe.2023.3253761.
Luis, F., P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, D. Aguilà, J. I. Martínez, L. A. Barrios, and G. Aromí. 2020. “A Dissymmetric [Gd2] Coordination Molecular Dimer Hosting Six Addressable Spin Qubits.” Communications Chemistry 3(1):176. doi.org/10.1038/S42004-020-00422-W.
Luis, F., A. Repollés, M. J. Martínez-Pérez, D. Aguilà, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, A. Camón, J. Sesé, L. A. Barrios, and G. Aromí. 2011. “Molecular Prototypes for Spin-Based CNOT and SWAP Quantum Gates.” Physical Review Letters 107(11):117203. doi.org/10.1103/Physrevlett.107.117203.
Lukin, D. M., M. A. Guidry, and J. Vučković. 2020. “Integrated Quantum Photonics with Silicon Carbide: Challenges and Prospects.” PRX Quantum 1(2):020102. doi.org/10.1103/Prxquantum.1.020102.
Ma, H., M. Govoni, and G. Galli. 2020. “Quantum Simulations of Materials on Near-Term Quantum Computers.” npj Computational Materials 6(1):85. doi.org/10.1038/S41524-020-00353-Z.
Ma, H., N. Sheng, M. Govoni, and G. Galli. 2020. “First-Principles Studies of Strongly Correlated States in Defect Spin Qubits in Diamond.” Physical Chemistry Chemical Physics 22(44):25522–25527. doi.org/10.1039/D0CP04585C.
Macaluso, E., M. Rubín, D. Aguilà, A. Chiesa, L. A. Barrios, J. I. Martínez, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí, and S. Carretta. 2020. “A Heterometallic [LnLn′Ln] Lanthanide Complex as a Qubit with Embedded Quantum Error Correction.” Chemical Science 11(38):10337–10343. doi.org/10.1039/D0SC03107K.
Martinis, J. M., K. B. Cooper, R. Mcdermott, M. Steffen, M. Ansmann, K. D. Osborn, K. Cicak, S. Oh, D. P. Pappas, R. W. Simmonds, and C. C. Yu. 2005. “Decoherence in Josephson Qubits from Dielectric Loss.” Physical Review Letters 95(21):210503. doi.org/10.1103/Physrevlett.95.210503.
McArdle, S., S. Endo, A. Aspuru-Guzik, S. C. Benjamin, and X. Yuan. 2020. “Quantum Computational Chemistry.” Reviews of Modern Physics 92(1):015003. https://doi.org/10.1103/RevModPhys.92.015003.
McClean, J. R., J. Romero, R. Babbush, and A. Aspuru-Guzik. 2016. “The Theory of Variational Hybrid Quantum-Classical Algorithms.” New Journal of Physics 18(2):023023. doi.org/10.1088/1367-2630/18/2/023023.
McInnes, E. J. L. 2022. “Molecular Spins Clock in.” Nature Chemistry 14(4):361–362. doi.org/10.1038/S41557-022-00919-Y.
Miao, K. C., J. P. Blanton, C. P. Anderson, A. Bourassa, A. L. Crook, G. Wolfowicz, H. Abe, T. Ohshima, and D. D. Awschalom. 2020. “Universal Coherence Protection in a Solid-State Spin Qubit.” Science 369(6510):1493–1497. doi.org/10.1126/Science.Abc5186.
Morello, A., J. J. Pla, F. A. Zwanenburg, K. W. Chan, K. Y. Tan, H. Huebl, M. Möttönen, C. D. Nugroho, C. Yang, J. A. Van Donkelaar, A. D. C. Alves, D. N. Jamieson, C. C. Escott, L. C. L. Hollenberg, R. G. Clark, and A. S. Dzurak. 2010. “Single-Shot Readout of an Electron Spin in Silicon.” Nature 467(7316):687–691. doi.org/10.1038/Nature09392.
Moreno-Pineda, E., M. Damjanović, O. Fuhr, W. Wernsdorfer, and M. Ruben. 2017. “Nuclear Spin Isomers: Engineering a Et4N[DyPc2] Spin Qudit.” Angewandte Chemie International Edition 56(33):9915–9919. doi.org/10.1002/Anie.201706181.
Moreno-Pineda, E., C. Godfrin, F. Balestro, W. Wernsdorfer, and M. Ruben. 2018. “Molecular Spin Qudits for Quantum Algorithms.” Chemical Society Reviews 47(2):501–513. doi.org/10.1039/C5CS00933B.
Motta, M., D. M. Ceperley, G. K.-L. Chan, J. A. Gomez, E. Gull, S. Guo, C. A. Jiménez-Hoyos, T. N. Lan, J. Li, F. Ma, A. J. Millis, N. V. Prokof’ev, U. Ray, G. E. Scuseria, S. Sorella, E. M. Stoudenmire, Q. Sun, I. S. Tupitsyn, S. R. White, D. Zgid, and S. Zhang (Simons Collaboration on the Many-Electron Problem). 2017. “Towards the Solution of the Many-Electron Problem in Real Materials: Equation of State of the Hydrogen Chain with State-of-the-Art Many-Body Methods.” Physical Review X 7(3):031059. doi.org/10.1103/Physrevx.7.031059.
Nayak, C. 2021. “Full Stack Ahead: Pioneering Quantum Hardware Allows for Controlling up to Thousands of Qubits at Cryogenic Temperatures.” Microsoft Research. January 27, 2021. www.microsoft.com/en-us/research/blog/full-stack-aheadpioneering-quantum-hardware-allows-for-controlling-up-to-thousands-of-qubits-at-cryogenic-temperatures.
Nayak, C., S. H. Simon, A. Stern, M. Freedman, and S. Das Sarma. 2008. “Non-Abelian Anyons and Topological Quantum Computation.” Reviews of Modern Physics 80(3):1083–1159. doi.org/10.1103/Revmodphys.80.1083.
Noel, C., M. Berlin-Udi, C. Matthiesen, J. Yu, Y. Zhou, V. Lordi, and H. Häffner. 2019. “Electric-Field Noise from Thermally Activated Fluctuators in a Surface Ion Trap.” Physical Review A 99(6):063427. doi.org/10.1103/Physreva.99.063427.
O’Brien, T. E., G. Anselmetti, F. Gkritsis, V. E. Elfving, S. Polla, W. J. Huggins, O. Oumarou, K. Kechedzhi, D. Abanin, R. Acharya, I. Aleiner, R. Allen, T. I. Andersen, K. Anderson, M. Ansmann, F. Arute, K. Arya, A. Asfaw, J. Atalaya, D. Bacon, J. C. Bardin, A. Bengtsson, S. Boixo, G. Bortoli, A. Bourassa, J. Bovaird, L. Brill, M. Broughton, B. Buckley, D. A. Buell, T. Burger, B. Burkett, N. Bushnell, J. Campero, Y. Chen, Z. Chen, B. Chiaro, D. Chik, J. Cogan, R. Collins, P. Conner, W. Courtney, A. L. Crook, B. Curtin, D. M. Debroy, S. Demura, I. Drozdov, A. Dunsworth, C. Erickson, L. Faoro, E. Farhi, R. Fatemi, V. S. Ferreira, L. Flores Burgos, E. Forati, A. G. Fowler, B. Foxen, W. Giang, C. Gidney, D. Gilboa, M. Giustina, R. Gosula, A. Grajales Dau, J. A. Gross, S. Habegger, M. C. Hamilton, M. Hansen, M. P. Harrigan, S. D. Harrington, P. Heu, J. Hilton, M. R. Hoffmann, S. Hong, T. Huang, A. Huff, L. B. Ioffe, S. V. Isakov, J. Iveland, E. Jeffrey, Z. Jiang, C. Jones, P. Juhas, D. Kafri, J. Kelly, T. Khattar, M. Khezri, M. Kieferová, S. Kim, P. V. Klimov, A. R. Klots, R. Kothari, A. N. Korotkov, F. Kostritsa, J. M. Kreikebaum, D. Landhuis, P. Laptev, K. Lau, L. Laws, J. Lee, K. Lee, B. J. Lester, A. T. Lill, W. Liu, W. P. Livingston, A. Locharla, E. Lucero, F. D. Malone, S. Mandra, O. Martin, S. Martin, J. R. McClean, T. McCourt, M. McEwen, A. Megrant, X. Mi, A. Mieszala, K. C. Miao, M. Mohseni, S. Montazeri, A. Morvan, R. Movassagh, W. Mruczkiewicz, O. Naaman, M. Neeley, C. Neill, A. Nersisyan, H. Neven, M. Newman, J. H. Ng, A. Nguyen, M. Nguyen, M. Y. Niu, S. Omonije, A. Opremcak, A. Petukhov, R. Potter, L. P. Pryadko, C. Quintana, C. Rocque, P. Roushan, N. Saei, D. Sank, K. Sankaragomathi, K. J. Satzinger, H. F. Schurkus, C. Schuster, M. J. Shearn, A. Shorter, N. Shutty, V. Shvarts, J. Skruzny, V. Smelyanskiy, W. C. Smith, R. Somma, G. Sterling, D. Strain, M. Szalay,
D. Thor, A. Torres, G. Vidal, B. Villalonga, C. Vollgraff Heidweiller, T. White, B. W. K. Woo, C. Xing, Z. J. Yao, P. Yeh, J. Yoo, G. Young, A. Zalcman, Y. Zhang, N. Zhu, N. Zobrist, C. Gogolin, R. Babbush, and N. C. Rubin. 2022. “Purification-Based Quantum Error Mitigation of Pair-Correlated Electron Simulations.” ArXiv. doi.org/10.48550/arxiv.2210.10799.
O’Malley, P. J. J., R. Babbush, I. D. Kivlichan, J. Romero, J. R. McClean, R. Barends, J. Kelly, P. Roushan, A. Tranter, N. Ding, B. Campbell, Y. Chen, Z. Chen, B. Chiaro, A. Dunsworth, A. G. Fowler, E. Jeffrey, E. Lucero, A. Megrant, J. Y. Mutus, M. Neeley, C. Neill, C. Quintana, D. Sank, A. Vainsencher, J. Wenner, T. C. White, P. V. Coveney, P. J. Love, H. Neven, A. Aspuru-Guzik, and J. M. Martinis. 2016. “Scalable Quantum Simulation of Molecular Energies.” Physical Review X 6(3):031007. doi.org/10.1103/Physrevx.6.031007.
Paz-Silva, G. A., and D. A. Lidar. 2013. “Optimally Combining Dynamical Decoupling and Quantum Error Correction.” Scientific Reports 3(1):1530. doi.org/10.1038/srep01530.
Peng, B., and K. Kowalski. 2022. “Mapping Renormalized Coupled Cluster Methods to Quantum Computers through a Compact Unitary Representation of Nonunitary Operators.” Physical Review Research 4(4):043172. doi.org/10.1103/PhysRevResearch.4.043172.
Peruzzo, A., J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik, and J. L. O’Brien. 2014. “A Variational Eigenvalue Solver on a Photonic Quantum Processor.” Nature Communications 5(1):4213. doi.org/10.1038/Ncomms5213.
Philbin, J. P., and P. Narang. 2021. “Computational Materials Insights into Solid-State Multiqubit Systems.” PRX Quantum 2(3):030102. doi.org/10.1103/Prxquantum.2.030102.
Phillips, W. A. 1987. “Two-Level States in Glasses.” Reports on Progress in Physics 50(12):1657. doi.org/10.1088/0034-4885/50/12/003.
Pruitt, S. R., C. Bertoni, K. R. Brorsen, and M. S. Gordon. 2014. “Efficient and Accurate Fragmentation Methods.” Accounts of Chemical Research 47(9):2786–2794. doi.org/10.1021/Ar500097m.
Rabl, P., S. J. Kolkowitz, F. H. L. Koppens, J. G. E. Harris, P. Zoller, and M. D. Lukin. 2010. “A Quantum Spin Transducer Based on Nanoelectromechanical Resonator Arrays.” Nature Physics 6(8):602–608. doi.org/10.1038/Nphys1679.
Ray, K. G., B. M. Rubenstein, W. Gu, and V. Lordi. 2019. “Van der Waals-Corrected Density Functional Study of Electric Field Noise Heating in Ion Traps Caused by Electrode Surface Adsorbates.” New Journal of Physics 21(5):053043. doi.org/10.1088/1367-2630/Ab1875.
Reiher, M., N. Wiebe, K. M. Svore, D. Wecker, and M. Troyer. 2017. “Elucidating Reaction Mechanisms on Quantum Computers.” Proceedings of the National Academy of Sciences USA 114(29):7555–7560. doi.org/10.1073/Pnas.1619152114.
Rose, B. C., D. Huang, Z.-H. Zhang, P. Stevenson, A. M. Tyryshkin, S. Sangtawesin, S. Srinivasan, L. Loudin, M. L. Markham, A. M. Edmonds, D. J. Twitchen, S. A. Lyon, and N. P. De Leon. 2018. “Observation of an Environmentally Insensitive Solid-State Spin Defect in Diamond.” Science 361(6397):60–63. doi.org/10.1126/Science.Aao0290.
Rosen A. S., V. Fung, P. Huck, C. T. O’Donnell, M. K. Horton, D. G. Truhlar, K. A. Persson, J. M. Notestein, and R. Q Snurr. 2022. “High-Throughput Predictions of Metal–Organic Framework Electronic Properties: Theoretical Challenges, Graph Neural Networks, and Data Exploration.” npj Compuational Materials 8(1):112. doi.org/10.1038/s41524-022-00796-6.
Rosen A. S., S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein, and R. Q. Snurr. 2021. “Machine Learning the Quantum-Chemical Properties of Metal–Organic Frameworks for Accelerated Materials Discovery.” Matter 4(5):1578–1597. doi.org/10.1016/j.matt.2021.02.015.
Ryabinkin, I. G., S. N. Genin, and A. F. Izmaylov. 2019. “Constrained Variational Quantum Eigensolver: Quantum Computer Search Engine in the Fock Space.” Journal of Chemical Theory and Computation 15(1):249–255. doi.org/10.1021/Acs.Jctc.8b00943.
Salfi, J., J. A. Mol, R. Rahman, G. Klimeck, M. Y. Simmons, L. C. L. Hollenberg, and S. Rogge. 2016. “Quantum Simulation of the Hubbard Model with Dopant Atoms in Silicon.” Nature Communications 7(1):11342. doi.org/10.1038/ncomms11342.
Sandhoefer, B., and G. K.-L. Chan. 2016. “Density Matrix Embedding Theory for Interacting Electron-Phonon Systems.” Physical Review B 94(8):085115. doi.org/10.1103/Physrevb.94.085115.
Sangtawesin, S., B. L. Dwyer, S. Srinivasan, J. J. Allred, L. V. H. Rodgers, K. De Greve, A. Stacey, N. Dontschuk, K. M. O’Donnell, D. Hu, D. A. Evans, C. Jaye, D. A. Fischer, M. L. Markham, D. J. Twitchen, H. Park, M. D. Lukin, and N. P. De Leon. 2019. “Origins of Diamond Surface Noise Probed by Correlating Single-Spin Measurements with Surface Spectroscopy.” Physical Review X 9(3):031052. doi.org/10.1103/Physrevx.9.031052.
Schuch, N., and F. Verstraete. 2009. “Computational Complexity of Interacting Electrons and Fundamental Limitations of Density Functional Theory.” Nature Physics 5(10):732–735. https://doi.org/10.1038/nphys1370.
Scientific Library. n.d. “List of Quantum Chemistry and Solid State Physics Software.” Accessed April 12, 2023. https://www.scientificlib.com/en/Chemistry/ListQuantumChemistrySolidStatePhysicsSoftware.html.
Sedlacek, J. A., J. Stuart, D. H. Slichter, C. D. Bruzewicz, R. Mcconnell, J. M. Sage, and J. Chiaverini. 2018. “Evidence for Multiple Mechanisms Underlying Surface Electric-Field Noise in Ion Traps.” Physical Review A 98(6):063430. doi.org/10.1103/Physreva.98.063430.
Seifrid, M., R. Pollice, A. Aguilar-Granda, Z. M. Chan, K. Hotta, C. T. Ser, J. Vestfrid, T. C. Wu, and A. Aspuru-Guzik. 2022. “Autonomous Chemical Experiments: Challenges and Perspectives on Establishing a Self-Driving Lab.” Accounts of Chemical Research 55(17):2454–2466. doi.org/10.1021/Acs.Accounts.2c00220.
Seo, H., H. Ma, M. Govoni, and G. Galli. 2017. “Designing Defect-Based Qubit Candidates in Wide-Gap Binary Semiconductors for Solid-State Quantum Technologies.” Physical Review Materials 1(7):075002. doi.org/10.1103/Physrevmaterials.1.075002.
Shavitt, I., and R. J. Bartlett. 2009. Many-Body Methods in Chemistry and Physics: MBPT and Coupled-Cluster Theory, Cambridge Molecular Science. Cambridge: Cambridge University Press.
Sheng, N., C. Vorwerk, M. Govoni, and G. Galli. 2022. “Green’s Function Formulation of Quantum Defect Embedding Theory.” Journal of Chemical Theory and Computation 18(6):3512–3522. doi.org/10.1021/Acs.Jctc.2c00240.
Sheridan, E., T. F. Harrelson, E. Sivonxay, K. A. Persson, M. Altoé, I. Siddiqi, D. F. Ogletree, D. I. Santiago, and S. M. Griffin. 2021. “Microscopic Theory of Magnetic Disorder-Induced Decoherence in Superconducting Nb Films.” ArXiv preprint. arXiv:2111.11684.
Shiddiq, M., D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado, and S. Hill. 2016. “Enhancing Coherence in Molecular Spin Qubits via Atomic Clock Transitions.” Nature 531(7594):348–351. doi.org/10.1038/Nature16984.
Siddiqi, I. 2021. “Engineering High-Coherence Superconducting Qubits.” Nature Reviews Materials 6(10):875–891. doi.org/10.1038/S41578-021-00370-4.
Singh, M. K., G. Wolfowicz, J. Wen, S. E. Sullivan, A. Prakash, A. M. Dibos, D. D. Awschalom, F. J. Heremans, and S. Guha. 2022. “Development of a Scalable Quantum Memory Platform—Materials Science of Erbium-Doped TiO2 Thin Films on Silicon.” ArXiv preprint. arXiv:2202.05376.
Sørensen, M. A., H. Weihe, M. G. Vinum, J. S. Mortensen, L. H. Doerrer, and J. Bendix. 2017. “Imposing High-Symmetry and Tuneable Geometry on Lanthanide Centres with Chelating Pt and Pd Metalloligands.” Chemical Science 8(5):3566–3575. doi.org/10.1039/C7SC00135E.
Su, Y., D. W. Berry, N. Wiebe, N. Rubin, and R. Babbush. 2021. “Fault-Tolerant Quantum Simulations of Chemistry in First Quantization.” PRX Quantum 2(4):040332. doi.org/10.1103/Prxquantum.2.040332.
Sugisaki, K., H. Wakimoto, K. Toyota, K. Sato, D. Shiomi, and T. Takui. 2022. “Quantum Algorithm for Numerical Energy Gradient Calculations at the Full Configuration Interaction Level of Theory.” Journal of Physical Chemistry Letters 13(48):11105–11111. doi.org/10.1021/acs.jpclett.2c02737.
Sun, Q., and G. K.-L. Chan. 2016. “Quantum Embedding Theories.” Accounts of Chemical Research 49(12):2705–2712. doi.org/10.1021/Acs.Accounts.6b00356.
Szabo, A., and N. S. Ostlund. 1989. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. New York: McGraw-Hill.
Thiel, W. 2014. “Semiempirical Quantum–Chemical Methods.” WIREs Computational Molecular Science 4(2):145–157. doi.org/10.1002/wcms.1161.
Thiele, S., F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben, and W. Wernsdorfer. 2014. “Electrically Driven Nuclear Spin Resonance in Single-Molecule Magnets.” Science 344(6188):1135–1138. doi.org/10.1126/Science.1249802.
Tuckett, D. K., S. D. Bartlett, and S. T. Flammia. 2018. “Ultrahigh Error Threshold for Surface Codes with Biased Noise.” Physical Review Letters 120(5):050505. doi.org/10.1103/Physrevlett.120.050505.
Van Meter, R., and K. M. Itoh. 2005. “Fast Quantum Modular Exponentiation.” Physical Review A 71(5):052320. doi.org/10.1103/PhysRevA.71.052320.
von Kugelgen, S., M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski, and D. E. Freedman. 2021. “Spectral Addressability in a Modular Two Qubit System.” Journal of the American Chemical Society 143(21):8069–8077. https://doi.org/10.1021/jacs.1c02417.
Vorwerk, C., N. Sheng, M. Govoni, B. Huang, and G. Galli. 2022. “Quantum Embedding Theories to Simulate Condensed Systems on Quantum Computers.” Nature Computational Science 2(7):424–432. doi.org/10.1038/S43588-022-00279-0.
Wan, N. H., T.-J. Lu, K. C. Chen, M. P. Walsh, M. E. Trusheim, L. De Santis, E. A. Bersin, I. B. Harris, S. L. Mouradian, I. R. Christen, E. S. Bielejec, and D. Englund. 2020. “Large-Scale Integration of Artificial Atoms in Hybrid Photonic Circuits.” Nature 583(7815):226–231. doi.org/10.1038/S41586-020-2441-3.
Wang, C., C. Axline, Y. Y. Gao, T. Brecht, Y. Chu, L. Frunzio, M. H. Devoret, and R. J. Schoelkopf. 2015. “Surface Participation and Dielectric Loss in Superconducting Qubits.” Applied Physics Letters 107(16):162601. doi.org/10.1063/1.4934486.
Wang, D. S., M. Haas, and P. Narang. 2021. “Quantum Interfaces to the Nanoscale.” ACS Nano 15(5):7879–7888. doi.org/10.1021/acsnano.1c01255.
Weber, J. R., W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. Van De Walle, and D. D. Awschalom. 2010. “Quantum Computing with Defects.” Proceedings of the National Academy of Sciences USA 107(19):8513–8518. doi.org/10.1073/Pnas.1003052107.
Wecker, D., M. B. Hastings, and M. Troyer. 2015. “Progress Towards Practical Quantum Variational Algorithms.” Physical Review A 92(4):042303. doi.org/10.1103/Physreva.92.042303.
Weissman, S. A., and N. G. Anderson. 2015. “Design of Experiments (DoE) and Process Optimization. A Review of Recent Publications.” Organic Process Research & Development 19(11):1605–1633. doi.org/10.1021/Op500169m.
Williams, K. T., Y. Yao, J. Li, L. Chen, H. Shi, M. Motta, C. Niu, U. Ray, S. Guo, R. J. Anderson, J. Li, L. N. Tran, C.-N. Yeh, B. Mussard, S. Sharma, F. Bruneval, M. Van Schilfgaarde, G. H. Booth, G. K.-L. Chan, S. Zhang, E. Gull, D. Zgid, A. Millis, C. J. Umrigar, and L. K. Wagner (Simons Collaboration on the Many-Electron Problem). 2020. “Direct Comparison of Many-Body Methods for Realistic Electronic Hamiltonians.” Physical Review X 10(1):011041. doi.org/10.1103/Physrevx.10.011041.
Wineland, D. J., C. Monroe, W. M. Itano, D. Leibfried, B. E. King, and D. M. Meekhof. 1998. “Experimental Issues in Coherent Quantum-State Manipulation of Trapped Atomic Ions.” Journal of Research of the National Institute of Standards and Technology 103(3):259–328. doi.org/10.6028/Jres.103.019.
Wootters, W. K., and W. H. Zurek. 1982. “A Single Quantum Cannot Be Cloned.” Nature 299(5886):802–803. doi.org/10.1038/299802a0.
Xiong Y., C. Bourgois, N. Sheremetyeva, W. Chen, D. Dahliah, H. Song, S.M. Griffin, A. Sipahigil, and G. Hautier. 2023. “High-Throughput Identification of Spin-Photon Interfaces in Silicon.” ArXiv. arxiv.org/pdf/2303.01594.pdf.
Yamabayashi, T., M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli, and M. Yamashita. 2018. “Scaling Up Electronic Spin Qubits into a Three-Dimensional Metal–Organic Framework.” Journal of the American Chemical Society 140(38):12090–12101. doi.org/10.1021/Jacs.8b06733.
Yamamoto, K., D. Z. Manrique, I. T. Khan, H. Sawada, and D. M. Ramo. 2022. “Quantum Hardware Calculations of Periodic Systems with Partition-Measurement Symmetry Verification: Simplified Models of Hydrogen Chain and Iron Crystals.” Physical Review Research 4(3):033110. doi.org/10.1103/physrevresearch.4.033110.
Ye, M., H. Seo, and G. Galli. 2019. “Spin Coherence in Two-Dimensional Materials.” npj Computational Materials 5(1):44. doi.org/10.1038/S41524-019-0182-3.
Yu, C.-J., M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov, and D. E. Freedman. 2016. “Long Coherence Times in Nuclear Spin-Free Vanadyl Qubits.” Journal of the American Chemical Society 138(44):14678–14685. doi.org/10.1021/Jacs.6b08467.
Yu, C.-J., S. von Kugelgen, M. D. Krzyaniak, W. Ji, W. R. Dichtel, M. R. Wasielewski, and D. E. Freedman. 2020. “Spin and Phonon Design in Modular Arrays of Molecular Qubits.” Chemistry of Materials 32(23):10200–10206. doi.org/10.1021/Acs.Chemmater.0c03718.
Yu, C.-J., S. von Kugelgen, D. W. Laorenza, and D. E. Freedman. 2021. “A Molecular Approach to Quantum Sensing.” ACS Central Science 7(5):712–723. doi.org/10.1021/Acscentsci.0c00737.
Yu, P., J. Chen, M. Gomanko, G. Badawy, E. P. A. M. Bakkers, K. Zuo, V. Mourik, and S. M. Frolov. 2021. “Non-Majorana States Yield Nearly Quantized Conductance in Proximatized Nanowires.” Nature Physics 17(4):482–488. doi.org/10.1038/S41567-020-01107-W.
Zadrozny, J. M., A. T. Gallagher, T. D. Harris, and D. E. Freedman. 2017. “A Porous Array of Clock Qubits.” Journal of the American Chemical Society 139(20):7089–7094. doi.org/10.1021/jacs.7b03123.
Zhang, X., C. Wolf, Y. Wang, H. Aubin, T. Bilgeri, P. Willke, A. J. Heinrich, and T. Choi. 2022. “Electron Spin Resonance of Single Iron Phthalocyanine Molecules and Role of Their Non-Localized Spins in Magnetic Interactions.” Nature Chemistry 14(1):59–65. doi.org/10.1038/s41557-021-00827-7.
Zhao, L., J. Goings, K. Wright, J. Nguyen, J. Kim, S. Johri, K. Shin, W. Kyoung, J. I. Fuks, J.-K. K. Rhee, Y. M. Rhee, et al. 2022. “Orbital-Optimized Pair-Correlated Electron Simulations on Trapped-Ion Quantum Computers.” ArXiv preprint. doi.org/10.48550/arXiv.2212.02482.


































