2

Introduction to Encryption

Modern cryptography uses techniques from mathematics to accomplish a variety of goals, including keeping data secret, authenticating data, and detecting dishonest behavior. Some techniques are in widespread use today; others are emerging. Each will be discussed in turn.^1,2,3

CRYPTOGRAPHIC ALGORITHMS IN USE TODAY

This chapter begins by introducing the kinds of cryptographic algorithms most commonly used today. Historically, encryption was developed to ensure the confidentiality of data. Further cryptographic techniques in common use can be used to ensure the integrity or authenticity of data.

Private-Key Encryption

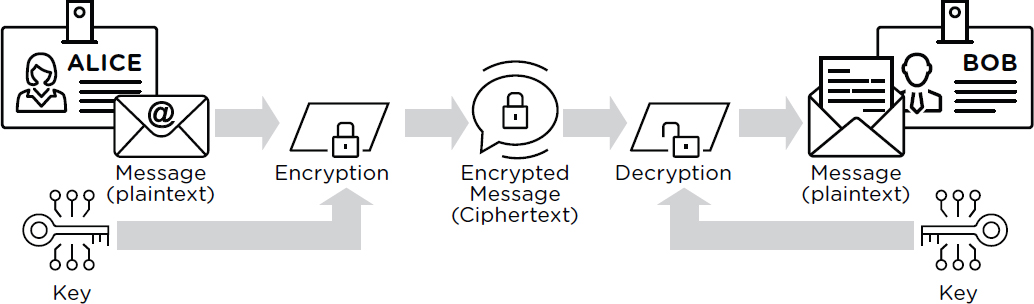
The simplest form of encryption is called private-key encryption or symmetric encryption.⁴ To keep information (called plaintext) secret, the sender encrypts it by applying an algorithm to the plaintext and key to obtain ciphertext. The recipient can apply a second algorithm to the matching decryption key and ciphertext to decrypt the ciphertext and recover the original plaintext, but without it the ciphertext reveals no meaningful information about the plaintext. Figure 2.1 illustrates the operation of private-key encryption.

The most commonly used private-key encryption algorithm today is the Advanced Encryption Standard (AES) algorithm, which was chosen by the National Institute of Standards and Technology (NIST) in 2001 through a

___________________

¹ D. Boneh and V. Shoup, 2020, “A Graduate Course in Applied Cryptography,” Version 0.5, January, http://toc.cryptobook.us.

² J. Katz and Y. Lindell, 2021, Introduction to Modern Cryptography, Boca Raton, FL: Chapman & Hall/CRC Press, Taylor & Francis Group.

³ O. Goldreich, 2004, Foundations of Cryptography, https://www.wisdom.weizmann.ac.il/~oded/foc.html.

⁴ O. Goldreich, S. Goldwasser, and S. Micali, 1986, How to construct random functions, Journal of the ACM 33(4):792–807, https://doi.org/10.1145/6490.6503.

public competition that solicited designs from cryptographers around the world.⁵ It is fast enough that with a little hardware support, it is unlikely to be a bottleneck in a computer system.⁶

Symmetric encryption is widely used today to protect the confidentiality of data both “at rest”—that is, in storage—and “in transit”—that is, in communications. For example, a disk encryption system uses symmetric encryption to encrypt a user’s data before writing it to disk and uses the same key to decrypt the data after reading from disk.⁷ Security of the system resides in the security of the key:⁸ an adversary who finds the key can also perform decryption (to steal the data) or encryption (to tamper with the data), so implementations use passwords, security hardware, or other measures to help protect keys.^9,10,11

Public-Key Encryption and Key Distribution

With private-key or symmetric encryption, the encryption and decryption keys are the same, but with public-key or asymmetric encryption,^12,13 they are different and knowing the encryption key does not enable decryption. This means that if a message recipient publishes the encryption key and keeps its matching decryption key secret, anyone can send messages that only the recipient can read. Figure 2.2 illustrates the operation of public-key encryption.

Public-key encryption is used in practice to solve the (private) key distribution problem—that is, how can two parties agree on a shared symmetric encryption key if they have never communicated before, and are

___________________

⁵ J. Daemen and V. Rijmen, 1999, “AES Proposal: Rijndael,” National Institute of Standards and Technology, March 9, https://csrc.nist.gov/csrc/media/projects/cryptographic-standards-and-guidelines/documents/aes-development/rijndael-ammended.pdf.

⁶ Intel, “Intel® Data Protection Technology with AES-NI and Secure Key,” https://www.intel.com/content/www/us/en/architecture-and-technology/advanced-encryption-standard-aes/data-protection-aes-general-technology.html, accessed October 5, 2021.

⁷ Dansimp, “Bitlocker (Windows 10)—Windows Security” (Windows 10)—Windows security | Microsoft Docs, https://docs.microsoft.com/en-us/windows/security/information-protection/bitlocker/bitlocker-overview, accessed October 5, 2021.

⁸ “The concept that in a sound cryptosystem, the security of information depends solely on the key, is referred to as Kerchoff’s principle.” See D. Khan, 1967, The Codebreakers: The Story of Secret Writing, New York: Macmillan, p. 235.

⁹ D. Boneh, S. Halevi, M. Hamburg, and R. Ostrovsky, 2008, “Circular-Secure Encryption from Decision Diffie-Hellman,” pp. 108–125 in Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-540-85174-5_7.

¹⁰ J. Katz, R. Ostrovsky, and M. Yung, 2001, “Efficient Password-Authenticated Key Exchange Using Human-Memorable Passwords,” pp. 475–494 in Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-44987-6_29.

¹¹ Wikipedia, “Trusted Platform Module,” Wikimedia Foundation, https://en.wikipedia.org/wiki/Trusted_Platform_Module, accessed October 14, 2021.

¹² S. Goldwasser and S. Micali, 1984, Probabilistic encryption, Journal of Computer and System Sciences 28(2):270–299, https://doi.org/10.1016/0022-0000(84)90070-9.

¹³ D. Boneh and V. Shoup, 2020, “A Graduate Course in Applied Cryptography,” Version 0.5, January, http://toc.cryptobook.us.

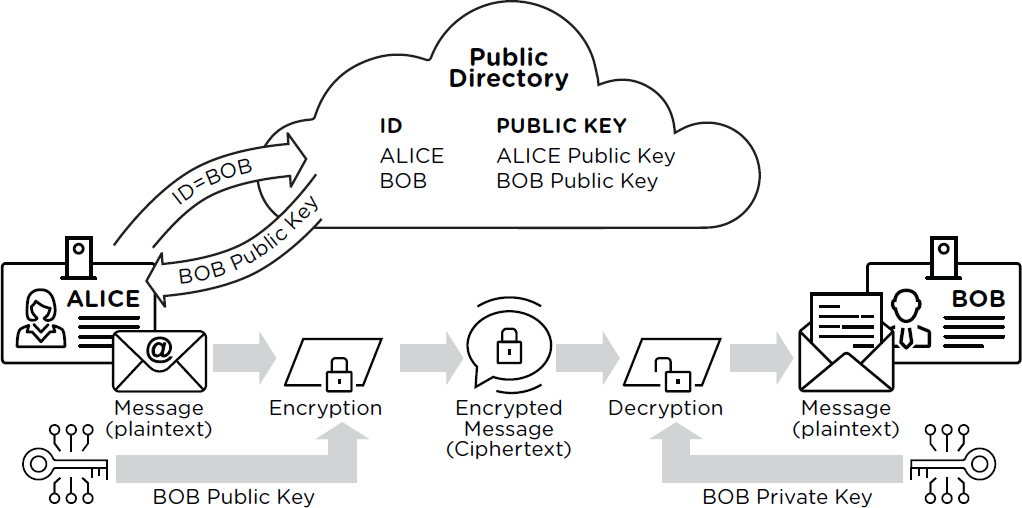
communicating over an untrusted channel? To solve this problem using public-key cryptography, one party can choose a random secret symmetric key, encrypt it with the other party’s public key, and send it to the other party. (Public-key encryption is much slower than symmetric encryption, so it is ordinarily used only to exchange private keys, and symmetric algorithms are used to protect the actual message data.¹⁴)

In 1976, Diffie and Hellman published a paper in the open literature that built on Merkle’s concept of public key cryptography¹⁵ and introduced the technique for key agreement that is now known as Diffie-Hellman key exchange.¹⁶ This algorithm is still used today in the form originally published, as well as a variant using elliptic curves (see below) that is somewhat more efficient. A widely used algorithm for public-key encryption is known as RSA, named for its creators Rivest, Shamir, and Adleman, who published the algorithm in 1977.¹⁷

To the non-technical person, public-key cryptography may seem like magic, as it depends on certain mathematical operations being easy to do but hard to undo. For example, the security of RSA depends on the fact that it is computationally fast to multiply two large prime integers but, as far is known, there is no computationally fast general algorithm to recover the two factors from the product with a classical computer. Elliptic curve cryptography, based on the algebraic structure of elliptic curves over finite fields, depends on the fact that it is easy to multiply a publicly known base point by a scalar value but as far as is known there is no computationally efficient algorithm to compute the corresponding scalar given just the base and target point.¹⁸

___________________

¹⁴ Ellis, Cocks, and Williamson developed ideas behind public-key cryptography, which they called “non-secret encryption,” in classified reports at GCHQ. This history has since been declassified. See J.H. Ellis, “The History of Non Secret Encryption,” last modified August 28, 2016, https://www.cs.miami.edu/home/burt/manuscripts/crypto_for_intelligence/ellis.pdf.

¹⁵ R. Merkle, “Secure Communications Over Insecure Channels,” http://www.merkle.com/1974/PuzzlesAsPublished.pdf.

¹⁶ W. Diffie and M. Hellman, 1976, New directions in cryptography, IEEE Transactions on Information Theory 22(6):644–654, https://doi.org/10.1109/tit.1976.1055638.

¹⁷ R.L. Rivest, A. Shamir, and L. Adleman, 1978, A method for obtaining digital signatures and public-key cryptosystems, Communications of the ACM 21(2):120–126, https://doi.org/10.1145/359340.359342.

¹⁸ D. Boneh and V. Shoup, 2020, “A Graduate Course in Applied Cryptography,” Version 0.5, January, http://toc.cryptobook.us.

To give a concrete use case, public-key cryptography is widely used as part of secure communications protocols on the Internet. The first step of many encrypted communications protocols like transport layer security (TLS), which is used to encrypt Hypertext Transfer Protocol Secure (HTTPS) web traffic, or Internet protocol security (IPsec), which is often used for virtual private networks (VPNs), is for both parties to perform a public key-based key exchange so that both sides agree on a shared secret to use for authentication and symmetric encryption.^19,20

Digital Signatures

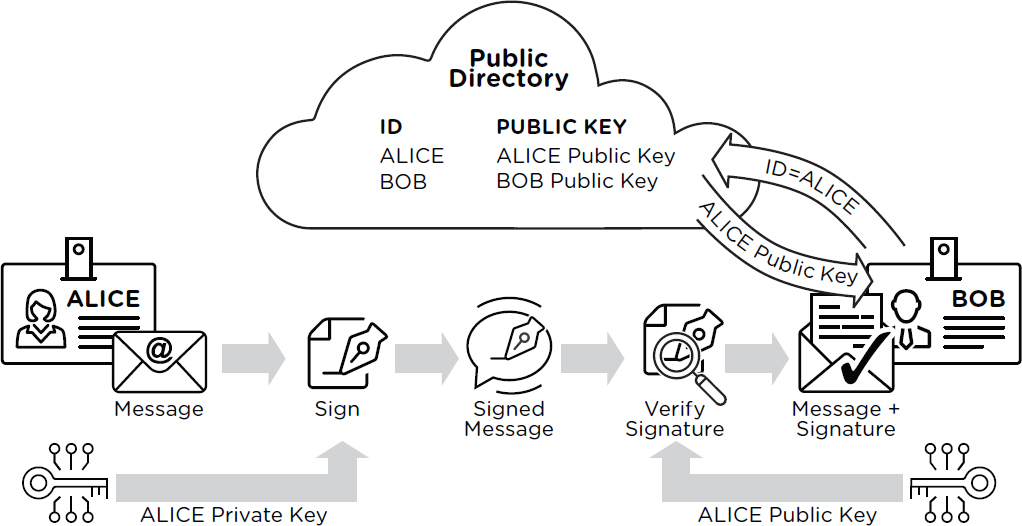
Digital signature schemes use mathematical techniques similar to those used in public-key encryption schemes, but with the specific purpose of authenticating data.²¹ A digital signature scheme allows anyone in possession of the public verification key to verify a digital signature of a message, but only someone in possession of the matching private signing key can sign the message. Figure 2.3 illustrates the operation of digital signature systems.

If a message originator publishes the verification key, anyone can check that the plaintext is the same as the message that was signed. If the signing key is kept secret, then only the entity with the private signing key could have generated a valid signature. Digital signature algorithms in common use today include the RSA digital signature algorithm and the Elliptic Curve Digital Signature Algorithm (ECDSA).^22,23

___________________

¹⁹ Wikipedia, “Transport Layer Security,” Wikimedia Foundation, https://en.wikipedia.org/wiki/Transport_Layer_Security, accessed October 6, 2021.

²⁰ Wikipedia, “IPsec,” Wikimedia Foundation, https://en.wikipedia.org/wiki/IPsec, accessed September 29, 2021.

²¹ S. Goldwasser, S. Micali, and R.L. Rivest, 1988, A digital signature scheme secure against adaptive chosen-message attacks, SIAM Journal on Computing 17(2):281–308, https://doi.org/10.1137/0217017.

²² R.L. Rivest, A. Shamir, and L. Adleman, 1978, A method for obtaining digital signatures and public-key cryptosystems, Communications of the ACM 21(2):120–126, https://doi.org/10.1145/359340.359342.

²³ D. Johnson, A. Menezes, and S. Vanstone, 2001, The Elliptic Curve Digital Signature Algorithm (ECDSA), International Journal of Information Security 1(1):36–63, https://doi.org/10.1007/s102070100002.

There are several major applications of public-key signature schemes. One is for software updates: the vendor signs the update, and then any client that knows the vendor’s public key can verify that the bits it is about to install actually came from the vendor. Other applications of digital signatures include authenticating user logins, securing credit card payments, cryptocurrencies, signing documents, and as a part of security protocols like TLS to detect tampering with messages. (See Box 2.1 for an introduction to TLS.)

Another use of digital signatures is to create digital certificates. A certificate is a digitally signed message that binds together a public key and an entity’s identity. For example, a certificate for a website includes the domain name (e.g., whitehouse.gov) and the web server’s public key. The digital signature on a certificate may be generated by a third party called a certificate authority; the certificate authority’s own verification key is usually distributed with an operating system or web browser. Often, there may be a chain of signed and trusted certificates and public keys that end in a key that is explicitly trusted. The security of a public key infrastructure using digital certificates also depends on policies and practices related to the issuance, storage, expiration, and revocation of credentials.^24,25

Collision-Resistant Hash Functions

A collision-resistant hash function boils down an arbitrarily large source message to a small output value called a hash (perhaps 256 bits) in such a way that finding a different source message with the same hash (a collision) takes too much computational power to be practical.^26,27 Unlike encryption functions, cryptographic hash functions in use today are not parameterized by a key; instead, for a given hash function the same input will always result in the same output. The SHA-2 algorithm is a common hash algorithm in use today, and the SHA-3 algorithm family is becoming more popular.²⁸ The MD5 hash algorithm is a historically very popular algorithm that remains in common use today, despite being known to be insecure because researchers have demonstrated how to produce collisions.^29,30 (See the section on Algorithm Transitions later in this chapter for a further discussion of attacks leveraging the insecurity of MD5.)

Hash functions are an important ingredient in many cryptographic applications, including most uses of digital signatures. The short, fixed-length output size of a hash function is useful because public-key signatures are slow. Applying a hash function to the message first means that the digital signature algorithm can be applied to the much shorter hash value. Hash functions have many other common uses, including being used to verify file integrity and to construct blockchains for cryptocurrencies.³¹

User Authentication

The above cryptographic tools can help secure protocols for user authentication and minimize information exposure if the system is compromised. For example, storing cryptographic hashes of passwords (rather than the passwords themselves) can make it somewhat more difficult for attackers who compromise a server to determine user passwords. Hardware-based tokens or keycards can use digital signatures to implement a challenge-response authentication protocol.

Biometrics are a class of authentication techniques that use properties of individuals (e.g., fingerprints, palm prints, iris scans, facial recognition, etc.) to authenticate presence instead of (or in addition to) cryptographic

___________________

²⁴ P.C. Kocher, 1998, “On Certificate Revocation and Validation,” pp. 172–177 in Financial Cryptography, https://doi.org/10.1007/bfb0055481.

²⁵ W. Aiello, S. Lodha, and R. Ostrovsky, 1998, “Fast Digital Identity Revocation,” pp. 137–152 in Advances in Cryptology—CRYPTO ‘98, https://doi.org/10.1007/bfb0055725.

²⁶ D. Boneh and V. Shoup, 2020, “A Graduate Course in Applied Cryptography,” Version 0.5, January, http://toc.cryptobook.us.

²⁷ Y. Ishai, E. Kushilevitz, and R. Ostrovsky, 2005, “Sufficient Conditions for Collision-Resistant Hashing,” pp. 445–456 in Theory of Cryptography, https://doi.org/10.1007/978-3-540-30576-7_24.

²⁸ Wikipedia, “SHA-2,” Wikimedia Foundation, https://en.wikipedia.org/wiki/SHA-2, accessed September 27, 2021.

²⁹ R. Rivest, 1992, “The MD5 Message-Digest Algorithm,” https://doi.org/10.17487/rfc1321.

³⁰ X. Wang and H. Yu, 2005, “How to Break MD5 and Other Hash Functions,” pp. 19–35 in Lecture Notes in Computer Science, https://doi.org/10.1007/11426639_2.

³¹ C. Badertscher, U. Maurer, D. Tschudi, and V. Zikas, 2017, “Bitcoin as a Transaction Ledger: A Composable Treatment,” pp. 324–356 in Advances in Cryptology—CRYPTO 2017, https://doi.org/10.1007/978-3-319-63688-7_11.

secrets known to the individual. Because it is difficult to memorize cryptographic keys, a common scenario for cryptographic key storage is to store the key on a device that uses a fingerprint reader or facial recognition to unlock access to the key.

Random Number Generators

Keys need to be unguessable, and one way to ensure this is to generate them at random. Computers can be equipped with hardware that allows them to collect environmental randomness by observing a physical phenomenon. For example, many central processing units (CPUs) today include hardware random number generators based on thermal noise. Approaches based on more exotic principles, such as radioactive decay or quantum optical sources, can also be theoretically sound, but are difficult or expensive to implement in practice. In recent years, quantum optical sources of randomness have become popular and may prove significantly faster than traditional techniques; however, they too are subject to failures such as producing less entropy than expected. Physical entropy sources may be slow or produce somewhat biased measurements (such as bits that do not have exactly 50 percent odds of being 0 versus 1), so modern computer systems use algorithms called pseudo-random number generators (PRNGs) that take as input an unpredictable starting string of bits (called a “seed”) and produce a much larger “random-looking” sequence of bits that cannot be distinguished from truly random bits without knowing the seed.^32,33 These algorithms are a fundamental building block for modern cryptography, and many constructions use symmetric ciphers, hash functions, or asymmetric ciphers as building blocks.³⁴

Box 2.2 defines blockchain and how it relates to cryptocurrencies.

___________________

³² M. Blum and S. Micali, 1984, How to generate cryptographically strong sequences of pseudorandom bits, SIAM Journal on Computing 13(4):850–864, https://doi.org/10.1137/0213053.

³³ O. Goldreich, S. Goldwasser, and S. Micali, 1986, How to construct random functions, Journal of the ACM 33(4):792–807, https://doi.org/10.1145/6490.6503.

³⁴ D. Boneh and V. Shoup, 2020, “A Graduate Course in Applied Cryptography,” Version 0.5, January, http://toc.cryptobook.us.

CRYPTANALYSIS AND FOUNDATIONS OF TRUST IN CRYPTOGRAPHY

The following paragraphs turn to a discussion of how the cryptographic community establishes trust in cryptographic algorithms.

There are multiple ways that encrypted data might be compromised by an adversary. First, an adversary could steal the key—for example, by compromising a person or computer that knows it. No matter how strong a cipher is, if the key is compromised, then anyone who gets access to the decryption key can decrypt and recover the encrypted data. Hiding the data necessarily requires keeping decryption keys secret.

Second, the cryptographic algorithm might contain a weakness that makes it practical for an adversary to decode the data without stealing the key. For example, in World War II, the Army Signals Intelligence Service was able to break the Japanese cipher code referred to as Purple by analyzing encrypted messages.³⁵

Modern ciphers are expected to withstand such attacks. Trust in cryptographic algorithms is built over time by community consensus about which algorithms resist all known cryptanalytic attacks. Over the past decades, cryptographers have rigorously defined various mathematical and security properties. When new algorithms and protocols are proposed, their designers often include statements about the intended security properties, as well as evidence such as proofs of equivalence to well-studied mathematical problems. Still, there is no absolute guarantee that any of the underlying mathematical problems cannot be solved efficiently.^36,37 As a result, confidence in systems involves public analysis of the designer’s assumptions and claims, and widely used algorithms are continuously analyzed by the international community of cryptography researchers. In addition, there are typically vast safety margins between the believed strength of a cipher and what adversaries can plausibly muster. For vendors, there is an increasing expectation that implementations should be subjected to security audits and testing.

Over the past decades, NIST has overseen the creation of several widely respected and adopted cryptographic algorithm standards. The first such standard issued by NIST was the Data Encryption Standard (DES),³⁸ a cryptographic block cipher designed by NIST in consultation with the National Security Agency (NSA) and based on a proposal submitted by IBM. When NIST determined in 1997 that it was time to retire DES and replace it with a new block cipher, NIST held a competition to select a new algorithm to be the replacement Advanced Encryption Standard (AES). NIST’s AES competition was an open, transparent, and public process, attracting 15 algorithm submissions from around the world. Over the next several years and after three rounds of public analysis, in 2000 NIST selected the Rijndael³⁹ submission as the winner and subsequently issued Federal Information Processing Standard (FIPS) 197, formally defining AES.

The process that NIST established and followed to select AES has become the benchmark for subsequent open and transparent algorithm competitions worldwide. NIST conducted an open competition to select the Secure Hash Algorithm-3 (SHA-3)⁴⁰ standard, receiving 51 candidate submissions in 2008 and eventually selecting the Keccak algorithm as the winner. Currently, NIST is conducting an open competition to select a set of post-quantum public-key cryptographic algorithms; more than 80 proposals from around the world were submitted to NIST’s post-quantum cryptography (PQC) standardization process⁴¹ in November 2017, and NIST is expected to select multiple winning algorithms starting in mid-2022.

___________________

³⁵ J.R. Leutze, 1983, “Ronald Lewin. The American Magic: Codes, Ciphers, and the Defeat of Japan,” American Historical Review, https://doi.org/10.1086/ahr/88.1.211.

³⁶ A prominent exception is the one-time pad, which Shannon proved was information-theoretically secure in a landmark paper. Unfortunately, the difficulty of properly generating and distributing key material renders the one-time pad difficult to impossible to use in practice, and there have been numerous intelligence failures owing to these usability issues.

³⁷ Such a proof would imply that P != NP, and would mean resolving one of the most famous unsolved problems in mathematics and computer science.

³⁸ NIST, 1977, “Data Encryption Standard,” Federal Information Processing Standards Publication 46, January 25.

³⁹ J. Daemen and V. Rijmen, 2005, “Rijndael/AES,” in Encyclopedia of Cryptography and Security (H.C.A. van Tilborg, ed.), https://doi.org/10.1007/0-387-23483-7_358.

⁴⁰ G. Bertoni, J. Daemen, M. Peeters, and G. Van Assche, 2013, “Keccak,” pp. 313–314 in Advances in Cryptology—EUROCRYPT 2013, https://doi.org/10.1007/978-3-642-38348-9_19.

⁴¹ NIST, “Post-Quantum Cryptography Standardization—Post-Quantum Cryptography,” Computer Security Resource Center, Information Technology Laboratory, https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization.

In addition to open competitions, sometimes NIST has partnered with other agencies or standards organizations to endorse cryptographic standards not produced by an open, transparent, and public process. For example, the 1995 SHA-1 hash algorithm standard and the 2000 SHA-2 family of hash algorithms were all developed initially by NSA and subsequently standardized by NIST. Another noteworthy standard not resulting from an open competition was the 2015 Dual Elliptic Curve Deterministic Random Bit Generator standard (DUAL-EC). Developed initially as part of an American National Standards Institute (ANSI) standards activity in which NIST participated, the DUAL-EC standard was recognized early on as having an unusual design structure with specific constants that had been defined by NSA. In 2007, Shumow and Ferguson⁴² showed that if the constants were constructed in a particular way, knowledge of that secret construction would allow one to predict outputs of the random number generator, thus compromising its security. Although there was no allegation in 2007 that the constants in the standard were deliberately constructed in this way, reporting following the 2013 Snowden disclosures alleged exactly this. The allegation (never confirmed or refuted by NSA) eventually led to the DUAL_EC_DRBG standard being retracted by NIST and removed from implementations around the world.⁴³

The DUAL_EC incident weakened confidence in NIST’s process for creating cryptographic standards. In response, NIST sponsored an external review of its processes by a committee appointed by its Visiting Committee on Advanced Technology (VCAT) and accepted the recommendations of the review.⁴⁴ The recommendations included increasing the openness and transparency of NIST’s processes for developing cryptographic standards, increasing NIST’s independent cryptographic capabilities, and clarifying the relationship between NIST and NSA with regard to the development of cryptographic standards. However, this incident led to lingering concerns about other NIST standards, particularly those related to elliptic curve cryptography. These concerns led some other standards bodies, most notably the Internet Engineering Task Force, to adopt additional elliptic curves in addition to the NIST-standardized curves. These additional curves did not go through a NIST competition or similar NIST standardization process, yet the end result was that NIST was forced to include them in a revision to NIST’s elliptic curve cryptography standard.

Thus, standards setting processes can be seen as dynamic. When new threats emerge, needs change, or scientific understanding improves, stronger algorithms are devised, studied, standardized, and deployed. Algorithms that do not come from an open process such as the one that NIST has frequently used, or that are not subject to years of public scrutiny, tend to be regarded as less likely to be secure. This skepticism has often been for good reason.^45,46 See for instance the example detailed in the article by Dunkelman, Keller, and Shamir.⁴⁷ Establishment of trust may involve different entities doing separate reviews. For example, multiple governments may separately review a cipher and conclude that it is acceptable for their own sensitive information.

Classical Cryptanalysis

If an adversary can correctly guess the value of a decryption key, the guessed key will decrypt the message, and security is compromised. Thus, to stop attacks that involve guessing secret keys, the number of possible

___________________

⁴² D. Shumow and N. Ferguson, 2007, “On the Possibility of a Back Door in the NIST SP800-90 Dual Ec Prng,” http://rump2007.cr.yp.to/15-shumow.pdf.

⁴³ D.J. Bernstein, T. Lange, and R. Niederhagen, 2016, “Dual EC: A Standardized Back Door,” pp. 256–281 in The New Codebreakers: Essays Dedicated to David Kahn on the Occasion of His 85th Birthday (P.Y.A. Ryan, D. Naccache, and J.-J. Naccache, eds.), Berlin: Springer, https://eprint.iacr.org/2015/767.

⁴⁴ NIST, 2014, “VCAT Report on NIST Cryptographic Standards and Guidelines Development Process,” July, https://www.nist.gov/system/files/documents/2017/05/09/VCAT-Report-on-NIST-Cryptographic-Standards-and-Guidelines-Process.pdf.

⁴⁵ E. Biham and L. Neumann, 2018, “Breaking the Bluetooth Pairing: Fixed Coordinate Invalid Curve Attack,” updated July 25, http://www.cs.technion.ac.il/~biham/BT.

⁴⁶ A. Biryukov, A. Shamir, and D. Wagner, 2001, “Real Time Cryptanalysis of A5/1 on a PC—Springer,” Chapter 10 in Fast Software Encryption (G. Goos, J. Hartmanis, J. van Leeuwen, and B. Schneier, eds.), FSE 2000, Lecture Notes in Computer Science, Volume 1978, Berlin, Heidelberg: Springer, https://doi.org/10.1007/3-540-44706-7_1.

⁴⁷ O. Dunkelman, N. Keller, and A. Shamir, 2010, “A Practical-Time Attack on the A5/3 Cryptosystem Used in Third Generation GSM Telephony,” https://eprint.iacr.org/2010/013; European Agency for Cybersecurity, 2017, “An Overview of the Wi-Fi WPA2 Vulnerability,” https://www.enisa.europa.eu/publications/info-notes/an-overview-of-the-wi-fi-wpa2-vulnerability.

cryptographic keys must be much larger than any plausible adversary could try. Current industry recommendations usually suggest at least 128 bits of security, so that the estimated running time of a brute-force attack (e.g., trying all possible 128-bit keys) would be 2 to the power of 128 (i.e., 2 * 2 * 2 * …* 2, or 340282366920938463 463374607431768211456).⁴⁸ To get a sense of the size of this number, an attacker with a billion computers, each trying a billion keys per second, would need 10.8 trillion years to try all values. When there are attacks against a cryptographic algorithm that can figure out the key or recover information about plaintexts faster than trying all possibilities, the “strength” of the algorithm is measured by the running time of the best-known attack.

For symmetric encryption algorithms such as AES that are believed to be secure, the best currently known attacks using classical computers are no faster than trying all possible keys. For collision-resistant hash functions such as SHA-3, the best-known attacks are exponential in half the output length. For example, SHA-3 with 256-bit output is believed to provide equivalent strength to AES-128.

In contrast, the known methods for constructing efficient public-key encryption and digital signature algorithms take advantage of sophisticated mathematical structures to enable the proper functioning of public-key cryptography. These mathematical operations make public-key encryption less efficient than the symmetric algorithms in common use (and thus make public-key encryption usable for key distribution but inefficient for protecting large messages). This mathematical structure means that some of these algorithms are vulnerable to attacks that are much more efficient than brute force, and thus require longer keys to achieve security levels equivalent to a desired bit strength.⁴⁹ For a 2048-bit RSA key, the best-known classical attack is estimated to be equivalent to brute-forcing a 112-bit symmetric key, and 3072-bit RSA is considered to provide 128-bit security. The security of elliptic curve–based public key systems scales differently, and a 256-bit elliptic curve key is currently considered to provide 128 bits of security against a classical computer.

Quantum Computing and Quantum Cryptanalysis

Since the 1990s, it has been known that quantum computers could theoretically break some (but not all) public-key cryptographic algorithms far faster than classical computers could do so. Sufficiently large quantum computers cannot yet be realized in practice, but if they are eventually developed then future adversaries might use them to decrypt communications that have previously been collected and archived.

Quantum computers use quantum mechanical effects in ways that are fundamentally different from classical computers. Where classical computers store information as binary digits—bits—that may be either 0 or 1 in value, quantum computers store information in quantum bits—qubits—that are two-state quantum mechanical systems that contain superpositions of both 0 and 1 values at the same time. Quantum computers use qubits and their quantum-mechanical properties like superposition and entanglement in order to perform some computations much faster than would be possible with a conventional computer.

Algorithms for quantum computers are described in terms of idealized “logical” qubits, but efforts to build quantum computers in the real world produce physical qubits that degrade quickly and exhibit errors when measured. At present, quantum computers consisting of a small number of physical qubits (fewer than 100) have been realized. (A different approach, taken by the company D-Wave Systems, is to build quantum computers that perform a process called “quantum annealing.” These computers can reach much larger numbers of qubits but cannot perform the operations needed to break RSA and other public key cryptosystems.) It is understood in theory how to use error correction techniques to combine many imperfect physical qubits into a single stable, logical qubit, but

___________________

⁴⁸ For classified uses up to TOP SECRET, NSA’s Commercial National Security Algorithms (CNSA) Suite specifies algorithms with at least 192 bits of security. See NSA, 2015, “Commercial National Security Algorithm Suite,” reviewed August 19, https://apps.nsa.gov/iaarchive/programs/iad-initiatives/cnsa-suite.cfm.

⁴⁹ The best public attacks against RSA moduli have been performed using the general Number Field Sieve (NFS). The RSA-768 challenge number, a 768-bit, 232-digit RSA modulus, was successfully factored in 2010 using NFS (see K. Aoki, J. Franke, A.K. Lenstra, E. Thomé, J.W. Bos, P. Gaudry, A. Kruppa, et al., 2010, “Factorization of a 768-bit RSA Modulus,” Version 1.4, February 18, https://eprint.iacr.org/2010/006.pdf). The current record for factoring was reported in February 2020 and is held by Boudot, Gaudry, Guillevic, Heninger, Thome, and Zimmermann (see P. Zimmermann, 2020, “[Cado-nfs-discuss] Factorization of RSA-250,” February 28, https://sympa.inria.fr/sympa/arc/cado-nfs/2020-02/msg00001.html), who factored the RSA-250 challenge number with NFS using approximately 2,700 core-years in total CPU time.

figuring out how to do so in practice and then scaling many logical qubits into a fault-tolerant quantum computer are areas of active research in the field of quantum computing.

Secret-key encryption and hash functions do not seem to have a mathematical structure that is amenable to attack by quantum computers beyond generic speedups for brute-force search. In particular, the best attacks currently known reduce the effective size of symmetric encryption keys by no more than a factor of 2. Equivalently, a brute-force key search on a quantum computer takes the square root of the running time it would take on a classical computer. This speedup is owing to Grover’s algorithm (1996), a quantum search algorithm.⁵⁰ In concrete terms, to find an AES-256 key, a quantum computer would need to perform at least as many operations as a classical computer would need to break AES-128—a huge number. (Quantum computers are not believed to provide any improvement against collision-resistant hash functions like SHA-3.) Thus, if large-scale fault-tolerant quantum computers are ever realized, symmetric key sizes must be doubled to maintain the same strength against attacks. In practice, this is reasonably straightforward, as symmetric algorithms such as AES that support 256-bit keys have been available for many years.

In contrast, all public-key schemes in common use today have a mathematical structure that allows an efficient attack given a sufficiently powerful quantum computer. The strength of the RSA cryptosystem is based on the difficulty of factoring, and an efficient quantum algorithm for factoring large numbers—Shor’s algorithm—was developed in 1994. Variants of Shor’s algorithm can break Diffie-Hellman key agreement and the elliptic curve-based algorithms Elliptic Curve Diffie-Hellman (ECDH) and ECDSA. Although the number of qubits needed depends on the public-key algorithm and size of the public key, at about 2400 logical qubits quantum computers would start to break modern public-key implementations.

The threat of future cryptographically relevant quantum computers has already spurred preparations for migrating to new, quantum-resistant public-key algorithms. Currently, NIST is running a multi-year open competition to produce recommended algorithms for key exchange, public key encryption, and digital signatures that are resistant to attacks by quantum computers.⁵¹ The new algorithms need to have a mathematical structure that is entirely different from common algorithms in use today in order to escape known attacks by quantum computers. Such algorithms are commonly called “post-quantum” or “quantum-resistant” cryptography.⁵²

The new cryptographic algorithms under consideration are based on a few different families of mathematical hardness assumptions. One of these new candidate assumptions, which underlies several of the encryption and signature algorithms under consideration as of this writing, is that finding a shortest non-zero vector in a high-dimensional lattice is difficult even for quantum computers.⁵³ Other candidate encryption and digital signature algorithms include algorithms based on the difficulty of decoding certain error-correcting codes, solving systems of multivariate equations, and schemes based on non-interactive, zero-knowledge protocols (see below).

For digital signatures, some quantum-resistant approaches, referred to as stateful digital signature, are constructed using only collision-resistant hash functions.^54,55 These are very efficient, and do not rely on the relatively new and more structured mathematical assumptions of the other quantum-resistant public key algorithms.

___________________

⁵⁰ L.K. Grover, 1996, “A Fast Quantum Mechanical Algorithm for Database Search,” Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing—STOC ‘96, https://doi.org/10.1145/237814.237866.

⁵¹ NIST, “Post-Quantum Cryptography Standardization—Post-Quantum Cryptography,” Computer Security Resource Center, Information Technology Laboratory, https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization.

⁵² Post-quantum encryption algorithms are so named because they are intended to resist cryptanalysis by a quantum computer. They run on a conventional computer (not a quantum computer) and are unrelated to quantum key distribution or quantum networks (discussed below).

⁵³ D. Micciancio and S. Goldwasser, 2002, “Cryptographic Functions,” pp. 143–194 in Complexity of Lattice Problems, https://doi.org/10.1007/978-1-4615-0897-7_8.

⁵⁴ M. Chase, D. Derler, S. Goldfeder, C. Orlandi, S. Ramacher, C. Rechberger, D. Slamanig, and G. Zaverucha, 2017, “Post-Quantum Zero-Knowledge and Signatures from Symmetric-Key Primitives,” Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, https://doi.org/10.1145/3133956.3133997.

⁵⁵ Y. Ishai, E. Kushilevitz, R. Ostrovsky, and A. Sahai, 2009, Zero-knowledge proofs from secure multiparty computation, SIAM Journal on Computing 39(3):1121–1152, https://doi.org/10.1137/080725398.

The NIST effort has strong support from the international cryptographic community and the recommendations that will be published soon are expected to be widely implemented. For implementers, the transition is expected to be difficult and expensive. (See the discussion of the Systems Driver in Chapter 4.) The new candidate post-quantum public-key algorithms currently have longer public keys, longer ciphertexts or signatures, or longer encryption, decryption, or signature verification times compared to public-key algorithms in wide use today. These differences can be significant disadvantages: slower cryptographic operations will require more computational power and slow down network communications; larger keys, ciphertexts, or signatures will require more data transfer and may exceed hard-coded or intrinsic limits on some systems. These differences will result in complicated implementation and transition problems and may result in vulnerabilities in implementations or protocols that hope to use these algorithms as drop-in replacements.

Key distribution centers (KDCs), a technology that can support the distribution of the symmetric key without relying on public-key encryption algorithms, are described in Box 2.3.

Algorithm Transitions

There are several historical examples of widely used cryptographic algorithms being replaced owing to cryptanalytic attacks. These examples can be informative when contemplating the upcoming transition to post-quantum algorithms.

A common challenge is that implementations must often include backward compatibility, even for insecure algorithms, during the transition in order to maintain a functioning system. Users, however, have relatively little impetus to upgrade while backward compatibility works. As a result, insecure algorithms live on even though they are known to be flawed. For example, the MD5 hash function was widely used through the 1990s and early 2000s despite the algorithm containing known flaws; the first collision was demonstrated in 2004, rendering the algorithm insecure, but it has remained in use for years after.⁵⁶ A set of academic researchers carried out a proof-of-concept attack using MD5 weaknesses to issue themselves a malicious certificate authority certificate in 2009, and the authors of the Flame malware used an MD5 collision attack against a portion of Microsoft’s certificate infrastructure in 2010 in order to create a fake signing certificate for the malware that passed verification. The first better-than-brute-force attack against the SHA-1 hash algorithm was published in 2005, and the first SHA-1 hash collision was demonstrated in 2017, but SHA-1 remains in widespread use.⁵⁷

Another illustrative example is the transition from the severely flawed SSL 2.0. Even though SSL 2.0 was superseded by a new version in 1996, many servers provided backward compatibility support for SSL 2.0. Twenty years later, in 2016, researchers found that hundreds of major websites were vulnerable⁵⁸ because they still supported SSL 2.0 and used the same RSA private key with SSL 2.0 and newer versions.⁵⁹

NIST and other organizations are well aware of the challenges posed by algorithm transitions in general, and by the complexity of the anticipated transition to post-quantum encryption algorithms. The Department of Homeland Security has collaborated with NIST on the development of a roadmap for the transition to post-quantum encryption and some private sector organizations have also begun to create and document plans and strategies for managing the transition.^60,61

The Future Threat to Collected Encrypted Data

When organizations deploy encryption to protect data at rest or in transit, they expect the encryption to protect their data against an adversary that has access to the ciphertext. In this scenario, the encryption needs to be secure against the adversary’s current decryption capabilities as well as the adversary’s future capabilities for as long as the content of the data is considered sensitive, in the event that the adversary collects the ciphertext and stores it for future analysis.

Providing security guarantees in this scenario means making assumptions about the strength of cryptographic algorithms against future cryptanalytic breakthroughs, evaluations of key length, and predictions for future changes to computer processing power. Breakthroughs in computing such as the emergence of quantum computers or a new approach to classical cryptanalysis have the potential to undermine prior assumptions about the strength of algorithms, and thus the protection afforded to encrypted data captured by an adversary. The risk that encrypted data will be intercepted, saved, and later decrypted has been long understood. In the NSA and Government Communications Headquarters (GCHQ) Venona project, Soviet messages intercepted and archived in the early 1940s continued to be analyzed and broken by the NSA and GCHQ through the late 1970s.⁶² Guidance on the use and upgrading of cryptographic systems reflects this understanding of the threat of future decryption and attempts to mitigate that threat.

___________________

⁵⁶ X. Wang and H. Yu, 2005, “How to Break MD5 and Other Hash Functions,” pp. 19–35 in Lecture Notes in Computer Science, https://doi.org/10.1007/11426639_2.

⁵⁷ M. Stevens, E. Bursztein, P. Karpman, A. Albertini, and Y. Markov, 2017, “The First Collision for Full SHA-1,” pp. 570–596 in Advances in Cryptology—CRYPTO 2017, https://doi.org/10.1007/978-3-319-63688-7_19.

⁵⁸ N. Aviram, S. Schinzel, J. Somorovsky, N. Heninger, M. Dankel, J. Steube, L. Valenta, et al., 2016, “DROWN: Breaking TLS Using SSLv2,” 25th USENIX Security Symposium, August.

⁵⁹ M. Stevens, E. Bursztein, P. Karpman, A. Albertini, and Y. Markov, 2017, “The First Collision for Full SHA-1,” pp. 570–596 in Advances in Cryptology—CRYPTO 2017, https://doi.org/10.1007/978-3-319-63688-7_19.

⁶⁰ Department of Homeland Security, “Post-Quantum Cryptography,” https://www.dhs.gov/quantum, accessed October 5, 2021.

⁶¹ SAFECode, “Post Quantum Crypto Archives,” https://safecode.org/category/post-quantum-crypto, accessed October 12, 2021.

⁶² NSA, n.d., “The Venona Story,” https://www.nsa.gov/portals/75/documents/about/cryptologic-heritage/historical-figures-publications/publications/coldwar/venona_story.pdf.

Organizations that are concerned about the security of their data going forward will need to upgrade systems to use quantum-resistant algorithms. National expert agencies such as NIST and NSA in the United States and NCSC in the United Kingdom are tasked with providing relevant algorithm recommendations and standards. These organizations are well aware of the future threat to stored encrypted data through advances in cryptanalysis and take these risks into account when providing recommendations.

EMERGING TECHNOLOGIES

The previous sections described cryptographic algorithms that are widely used today. This section introduces techniques that are not widely adopted, often because they are new, are not well understood, or have technical limitations that might be overcome through future research.

Zero Knowledge Proofs

Zero knowledge (ZK) proofs permit one computer (typically called a “Prover”) to convince another computer (typically called a “Verifier”) that the Prover knows some fact without revealing the fact to the Verifier.^63,64,65 Zero knowledge is used in cryptocurrency applications to hide the public keys of transaction participants (Zcash).^66,67 More recently, zero knowledge proofs have been used as the basis of post-quantum digital signature algorithms (NIST-Picnic).^68,69

There have been suggestions that the application of technologies such as zero knowledge can improve citizens’ trust in the Intelligence Community and government processes broadly. In general, the committee is skeptical that initiatives by the Intelligence Community based on zero knowledge or other advanced cryptographic methods will create (or substitute for) trust in the Intelligence Community. Fundamentally, trust is a social process, and technical tools cannot replace non-technical foundations of trust. One reason is that mathematical constructions generally do not map precisely to real-world concerns, so cryptographic proofs will not preclude the possibility of Intelligence Community misbehavior. Outside observers will generally lack the expertise, resources, and access required to assess the underlying mathematics, implementation correctness, and operational details to the degree required to establish trust. In contexts where there are conflicting motives (such as privacy regulations impacting

___________________

⁶³ S. Goldwasser, S. Micali, and C. Rackoff, 1989, The knowledge complexity of interactive proof systems, SIAM Journal on Computing 18(1):186–208, https://doi.org/10.1137/0218012.

⁶⁴ M. Blum, P. Feldman, and S. Micali, 1988, “Non-Interactive Zero-Knowledge and Its Applications,” Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing—STOC ‘88, https://doi.org/10.1145/62212.62222.

⁶⁵ J. Baron, “Securing Information for Encrypted Verification and Evaluation (SIEVE),” DARPA RSS, https://www.darpa.mil/program/securing-information-for-encrypted-verification-and-evaluation, accessed October 22, 2021.

⁶⁶ N. Bitansky, A. Chiesa, Y. Ishai, O. Paneth, and R. Ostrovsky, 2013, “Succinct Non-Interactive Arguments via Linear Interactive Proofs,” pp. 315–333 in Theory of Cryptography, https://doi.org/10.1007/978-3-642-36594-2_18.

⁶⁷ E. Ben Sasson, A. Chiesa, C. Garman, M. Green, I. Miers, E. Tromer, and M. Virza, 2014, “Zerocash: Decentralized Anonymous Payments from Bitcoin,” 2014 IEEE Symposium on Security and Privacy, https://doi.org/10.1109/sp.2014.36.

⁶⁸ M. Chase, D. Derler, S. Goldfeder, C. Orlandi, S. Ramacher, C. Rechberger, D. Slamanig, and G. Zaverucha, 2017, “Post-Quantum Zero-Knowledge and Signatures from Symmetric-Key Primitives,” Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, https://doi.org/10.1145/3133956.3133997.

⁶⁹ Y. Ishai, E. Kushilevitz, R. Ostrovsky, and A. Sahai, 2009, Zero-knowledge proofs from secure multiparty computation, SIAM Journal on Computing 39(3):1121–1152, https://doi.org/10.1137/080725398.

Intelligence Community mission effectiveness, or where Intelligence Community organizations with offensive roles are making proposals related to defense), skeptics may also suspect intentional backdoors or view proposals as an attempt to divert discussions about topics such as independent oversight or internal culture. On the other hand, these techniques may be useful in the context of interactions between intelligence or defense organizations in the United States or internationally.⁷⁰

Threshold Cryptography

Secret-sharing techniques enable splitting a key or other sensitive data into multiple parts held by different parties or devices, so that qualified sets of participants can reconstruct the secret.^71,72 The secret remains secure if any lesser group misbehaves or is compromised.

Threshold cryptosystems extend this idea to allow two or more participants to cooperate in performing a sensitive computation, where the security and privacy can be preserved even if one or several parties are compromised or act maliciously.^73,74,75,76 For example, threshold systems have been proposed for many other cryptographic primitives, including encryption, signature, and key agreement.^77,78,79

Computing on Encrypted Data

With most encryption algorithms in use today, the only operation performed on ciphertext is to decrypt it into readable form. For example, when Microsoft’s disk encryption feature (BitLocker) protects data at rest or protocols like TLS/SSL protect data in transit, the main cryptographic objective is to ensure that encrypted data cannot be used unless it has been decrypted.

___________________

⁷⁰ See S. Philippe, R. Goldston, A. Glaser, and F. d’Errico, 2016, A physical zero-knowledge object-comparison system for nuclear warhead verification, Nature Communications 7:12890, https://doi.org/10.1038/ncomms12890; A. Segal, J. Feigenbaum, and B. Ford, 2016, “Open, Privacy-Preserving Protocols for Lawful Surveillance,” July 13, https://arxiv.org/abs/1607.03659; A. Segal, J. Feigenbaum, and B. Ford, “Privacy-Preserving Lawful Contact Chaining, Preliminary Report,” http://www.cs.yale.edu/homes/jf/SFF-WPES2016.pdf; A. Bates, K.R.B. Butler, M. Sherr, C. Shields, P. Traynor, and D. Wallach, 2015, Accountable wiretapping-or-I know they can hear you now, Journal of Computer Security 23(2):167–195, https://doi.org/10.3233/JCS-140515; and B. Hemenway, S. Lu, R. Ostrovsky, and W. Welser IV, “High-Precision Secure Computation of Satellite Collision Probabilities,” in Security and Cryptography for Networks (V. Zikas and R. De Prisco, eds.), SCN 2016, Lecture Notes in Computer Science, Volume 9841, Springer, Cham, https://doi.org/10.1007/978-3-319-44618-9_9.

⁷¹ NIST, “Multi-Party Threshold Cryptography,” Computer Security Resource Center, Information Technology Laboratory, https://csrc.nist.gov/projects/threshold-cryptography, accessed October 8, 2021.

⁷² A. Beimel, 2011, “Secret-Sharing Schemes: A Survey,” pp. 11–46 in Lecture Notes in Computer Science, https://doi.org/10.1007/978-3-642-20901-7_2.

⁷³ O. Goldreich, S. Micali, and A. Wigderson, 2019, “How to Play Any Mental Game, or a Completeness Theorem for Protocols with Honest Majority,” Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, https://doi.org/10.1145/3335741.3335755.

⁷⁴ M. Ben-Or, S. Goldwasser, and A. Wigderson, 2019, “Completeness Theorems for Non-Cryptographic Fault-Tolerant Distributed Computation,” Providing Sound Foundations for Cryptography: On the Work of Shafi Goldwasser and Silvio Micali, https://doi.org/10.1145/3335741.3335756.

⁷⁵ D. Chaum, C. Crépeau, and I. Damgård, 1988, “Multiparty Unconditionally Secure Protocols,” Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing—STOC ‘88, https://doi.org/10.1145/62212.62214.

⁷⁶ R. Cramer, I.B. Damgård, and J.B. Nielsen, 2015, Secure Multiparty Computation and Secret Sharing, Cambridge, UK: Cambridge University Press.

⁷⁷ D. Boneh, X. Boyen, and S. Halevi, 2006, “Chosen Ciphertext Secure Public Key Threshold Encryption Without Random Oracles,” pp. 226–243 in Topics in Cryptology—CT-RSA 2006, https://doi.org/10.1007/11605805_15.

⁷⁸ V. Shoup, 2000, “Practical Threshold Signatures,” pp. 207–220 in Advances in Cryptology—EUROCRYPT 2000, https://doi.org/10.1007/3-540-45539-6_15.

⁷⁹ D. Harnik, J. Kilian, M. Naor, O. Reingold, and A. Rosen, 2005, “On Robust Combiners for Oblivious Transfer and Other Primitives,” pp. 96–113 in Lecture Notes in Computer Science, https://doi.org/10.1007/11426639_6.

Some new cryptographic techniques, including fully homomorphic encryption (FHE) and secure multi-party computation (MPC), are different.^80,81,82,83 FHE allows a participant to perform arbitrary computation on encrypted data. MPC allows two or more participants to compute certain information on joint data without ever disclosing this data either to outside adversaries or even to each other. Such techniques could allow organizations to gain intelligence across siloed datastores that cannot be joined.^{84,85,86,87,88,89} In theory, entirely untrusted cloud computers could perform general-purpose calculations without ever being able to see the underlying data.

FHE allows a computer to perform computations on encrypted data generating encrypted answers; the answers are available only to an entity that has the decryption key. MPC allows groups of machines to jointly compute functions of secret-shared data. The result of an MPC is the secret-shared output of the computation, which can then be sent to one or several parties for reconstruction. Many MPC protocols also have the benefit that even if a subset of parties misbehave, the computation is still performed correctly.⁹⁰

With present constructions, MPC involves more communication than FHE but is several orders of magnitude more efficient. While FHE is currently about 10,000 to 100,000 times slower than unencrypted computation⁹¹ and works only in the so-called circuit model of computation (where programs must be converted to digital circuits with addition and multiplication “gates”⁹²), MPC has progressed much further in performance, and is often a far better alternative to FHE. For example, as of 2012, MPC could support a million operations per second on encrypted data.⁹³ Since 2012, MPC research has progressed even further and performance at the level of 10×–100× slowdown compared to unencrypted computation can be achieved in some cases. For MPC, there are benchmarks for database operations that are 5 to 10 times slower than SQL.⁹⁴ Unlike FHE, there are MPC techniques to support random access into an array in constant, rather than linear time.⁹⁵ The state of the art in zero knowledge proofs

___________________

⁸⁰ See the Palisade Homomorphic Encryption Software Library website at https://palisade-crypto.org, accessed October 8, 2021.

⁸¹ S. Halevi and V. Shoup, 2020, “Design and Implementation of HElib: A Homomorphic Encryption Library,” Cryptology ePrint Archive, https://eprint.iacr.org/2020/1481.

⁸² EMP, “Toolkit: EMP-Tool,” https://emp-toolkit.github.io/emp-doc/html/md___users_wangxiao_git_emp-toolkit_emp-readme__r_e_a_d_m_e.html, accessed October 8, 2021.

⁸³ KU Leuven, “SCALE-MAMBA Software,” https://homes.esat.kuleuven.be/~nsmart/SCALE, accessed October 11, 2021.

⁸⁴ Boston Women’s Workforce Council, “Data Privacy,” https://thebwwc.org/mpc, accessed October 8, 2021.

⁸⁵ HAIC Helsinki-Aalto Institute for Cybersecurity, 2018, “HAIC Talk: The Advertisement Exchange—with Moti Yung,” YouTube, August 2, https://www.youtube.com/watch?v=bMl2PFU7gMA.

⁸⁶ A. Walker, S. Patel, and M. Yung, 2019, “Helping Organizations Do More Without Collecting More Data,” Google Security Blog, June 19, 2019, https://security.googleblog.com/2019/06/helping-organizations-do-more-without-collecting-more-data.html.

⁸⁷ Apple, 2021, “Apple and Google Partner on COVID-19 Contact Tracing Technology,” Newsroom, August 6, https://www.apple.com/newsroom/2020/04/apple-and-google-partner-on-covid-19-contact-tracing-technology.

⁸⁸ M. Ion, B. Kreuter, A.E. Nergiz, S. Patel, S. Saxena, K. Seth, M. Raykova, D. Shanahan, and M. Yung, 2020, “On Deploying Secure Computing: Private Intersection-Sum-with-Cardinality,” pp. 370–389 in 2020 IEEE European Symposium on Security and Privacy (EuroS&P), https://doi.org/10.1109/eurosp48549.2020.00031.

⁸⁹ F.S. Dittmer, Y. Ishai, S. Lu, R. Ostrovsky, M. Elsabagh, N. Kiourtis, B. Schulte, and A. Stavrou, 2020, “Function Secret Sharing for PSI-CA: With Applications to Private Contact Tracing,” CoRR abs/2012.13053.

⁹⁰ V. Goyal, H. Li, R. Ostrovsky, A. Polychroniadou, and Y. Song, 2021, “Atlas: Efficient and Scalable MPC in the Honest Majority Setting,” pp. 244–274 in Advances in Cryptology—CRYPTO 2021, https://doi.org/10.1007/978-3-030-84245-1_9.

⁹¹ A. Feldmann, N. Samardzic, A. Krastev, S. Devadas, R. Dreslinski, K. Eldefrawy, N. Genise, C. Peikert, and D. Sanchez, 2021, “F1: A Fast and Programmable Accelerator for Fully Homomorphic Encryption (Extended Version),” revised September 25, https://arxiv.org/abs/2109.05371.

⁹² A gate is a logical operation, such as addition or multiplication of two numbers, or a Boolean operation such as a logical and or a logical or. It is well known in computer science that any computer program can be represented as a collection of elementary gates. Computer hardware implemented in silicon consists of logical gates that can do elementary computation, and computers put these operations together to run arbitrary computer programs. Unfortunately, in cryptography, one must do the “reverse” and decompose computer programs into logical gates, as computing on encrypted data in FHE requires. For MPC, there is more flexibility about the model of computation.

⁹³ D. Bogdanov, M. Niitsoo, T. Toft, and J. Willemson, 2012, High-performance secure multi-party computation for data mining applications, International Journal of Information Security 11:403–418, https://link.springer.com/article/10.1007/s10207-012-0177-2.

⁹⁴ I. Yuval, E. Kushilevitz, S. Lu, and R. Ostrovsky, 2016, “Private large-scale databases with distributed searchable symmetric encryption.” In Cryptographers’ Track at the RSA Conference, pp. 90–107. Springer, Cham.

⁹⁵ R. Ostrovsky and V. Shoup, 1997, “Private information storage (extended abstract).” Symposium on Theory of Computing (STOC) ‘97.

is even more encouraging, and implementation can achieve 3×–5× slowdown compared to unencrypted execution of the same program.⁹⁶

There are special cases of MPC that, instead of supporting general computation, support only a specific computing task but are even more efficient than general-purpose MPC. One example is Function Secret Sharing (FSS), which allows two (or more) servers to compute simple aggregate statistics with privacy of input and output from the computing servers.^97,98,99,100 FSS is being deployed (as part of Prio) in the Mozilla Firefox Browser to compute users’ telemetry data in a privacy-preserving way. Two other examples of special-purpose MPC are so-called private set intersection (PSI) and private set union (PSU). Private set intersection allows two or more parties to find intersections of their secret sets of data without learning anything else, while private set union allows parties to find a union without finding out who contributed a specific item.

PSI has many applications in practice—for example, to manage allow lists or block lists privately, to privately check whether a password has been leaked, and to privately match ads displayed on the web to users. There have been proposals to use PSI to carry out law enforcement searches for user information without revealing non-matching data.^101,102,103 Google currently uses PSI to calculate statistics on the overlapping membership of data sets without sharing the underlying data sets.

There are also faster but limited-functionality variants of homomorphic encryption that are referred to as partially (or somewhat) homomorphic encryption. These variants, which for example support performing computations of limited complexity or using only addition operations, can be sufficient for tasks such as cryptographic tallying of votes and computation of statistics.¹⁰⁴ To give an idea of the current state of the art for a well-suited application, a 2020 proof-of-concept somewhat homomorphic computation of a “genome-wide association study” that involved computing a logistic regression homomorphically extrapolated a running time of 23 hours and several terabytes of RAM for a sample of 10,000 genomes and 500,000 markers;¹⁰⁵ a 2013 publication^106,107,108 suggested that an equivalent computation was doable in 7 minutes on a laptop.

___________________

⁹⁶ S. Dittmer, Y. Ishai, and R. Ostrovsky, 2020, “Line-point zero knowledge and its applications.” Cryptology ePrint Archive.

⁹⁷ E. Boyle, N. Gilboa, and Y. Ishai, 2016, “Function Secret Sharing.” Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, https://doi.org/10.1145/2976749.2978429.

⁹⁸ H. Corrigan-Gibbs and D. Boneh, 2017, “Prio: Private, Robust, and Scalable Computation of Aggregate Statistics,” pp. 259–282 in 14th USENIX Symposium on Networked Systems Design and Implementation, https://www.usenix.org/system/files/conference/nsdi17/nsdi17-corrigan-gibbs.pdf.

⁹⁹ S. Englehardt, 2019, “Next Steps in Privacy-Preserving Telemetry with Prio,” Mozilla Security Blog, June 6, https://blog.mozilla.org/security/2019/06/06/next-steps-in-privacy-preserving-telemetry-with-prio.

¹⁰⁰ S. Addanki, K. Garbe, E. Jaffe, R. Ostrovsky, and A. Polychroniadou, 2021, “Prio+: Privacy Preserving Aggregate Statistics via Boolean Shares,” Cryptology ePrint Archive, https://eprint.iacr.org/2021/576.

¹⁰¹ J. Feigenbaum and B. Ford, 2015, Seeking Anonymity in an Internet Panopticon, Communications of the ACM 58(10):58–69, https://doi.org/10.1145/2714561.

¹⁰² P. Rindal and P. Schoppmann, 2021, “Vole-Psi: Fast OPRF and Circuit-Psi from Vector-OLE,” pp. 901–930 in Annual International Conference on the Theory and Applications of Cryptographic Techniques, Springer.

¹⁰³ M. Rosulek and N. Trieu, 2021, “Compact and Malicious Private Set Intersection for Small Sets,” pp. 1166–1181 in Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security.

¹⁰⁴ P. Paillier, 2002, Composite-residuosity based cryptography: An overview, CryptoBytes 5(1).

¹⁰⁵ M. Blatt, A. Gusev, Y. Polyakov, and S. Goldwasser, 2020, Secure large-scale genome-wide association studies using homomorphic encryption, Proceedings of the National Academy of Sciences U.S.A. 117(21):11608–11613, https://www.pnas.org/content/117/21/11608.

¹⁰⁶ K. Sikorska, E. Lesaffre, P.F.J. Groenen, and P.H.C. Eilers, 2013, GWAS on your notebook: Fast semi-parallel linear and logistic regression for genome-wide association studies, BMC Bioinformatics 14:166, https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-14-166.

¹⁰⁷ P. Rindal and P. Schoppmann, 2021, “Vole-Psi: Fast OPRF and Circuit-Psi from Vector-OLE,” pp. 901–930 in Annual International Conference on the Theory and Applications of Cryptographic Techniques, Springer.

¹⁰⁸ M. Rosulek and N. Trieu, 2021, “Compact and Malicious Private Set Intersection for Small Sets,” pp. 1166–1181 in Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security.

Encrypted Data Storage and Retrieval

Specialized cryptographic techniques have been developed to help address security challenges involved with storing, searching, and retrieving information.^109,110,111 Searchable encryption refers to techniques that allow participants to perform limited kinds of queries on an encrypted database while concealing the contents of the database and the search queries from the computers hosting it. Oblivious Random Access Memory (ORAM) is a technique that can hide from a storage system which indices or files have been accessed or accessed more than once.¹¹² ORAM is used, for example, in the Signal messaging platform to perform contact discovery without revealing a user’s contact list to the untrusted machine performing the computation.¹¹³

Private Information Retrieval (PIR) is a technology that allows a user to send an encrypted query to a database, which “processes” the entire database and gives back a short, encrypted answer.^114,115,116 The database system that executes the query cannot determine what the query is. Although initial PIR schemes have been very inefficient, more efficient approaches involving off-line precomputation may be more practical.^117,118 These techniques allow one to select data to be uploaded to a more sensitive processing environment without revealing which data are being uploaded.

Program Obfuscation

In theory, a cryptographically secure method for program obfuscation would allow an entity to distribute a software program for performing some function (e.g., decrypting a ciphertext using a fixed secret key) that could be executed by a third party without revealing any information about the program’s execution (e.g., the value of the key used to decrypt) beyond the result.¹¹⁹

Engineering Alternatives to Cryptography’s Limitations

For many real-world data security problems, there are no purely cryptographic solutions, or the available cryptographic algorithms do not meet real-world efficiency constraints. For example, the existing cryptographically robust proposals for program obfuscation are so slow as to be unimplementable for real-world applications, but there is a market need for practical solutions in digital rights management and other applications. The

___________________

¹⁰⁹ D. Boneh, G. Di Crescenzo, R. Ostrovsky, and G. Persiano, 2004, “Public Key Encryption with Keyword Search,” pp. 506–522 in Advances in Cryptology—EUROCRYPT 2004, https://doi.org/10.1007/978-3-540-24676-3_30.

¹¹⁰ R. Curtmola, J. Garay, S. Kamara, and R. Ostrovsky, 2011, Searchable symmetric encryption: Improved definitions and efficient constructions, Journal of Computer Security 19(5):895–934, https://doi.org/10.3233/jcs-2011-0426.

¹¹¹ Intelligence Advanced Research Projects Agency, 2010, “SPAR: Security and Privacy Assurance Research,” Broad Agency Announcement IARPA-BAA-11-01, released December 29, https://www.iarpa.gov/index.php/research-programs/spar.

¹¹² O. Goldreich and R. Ostrovsky, 1996, Software protection and simulation on oblivious rams, Journal of the ACM 43(3):431–473, https://doi.org/10.1145/233551.233553.

¹¹³ Moxie0, 2017, “Technology Preview: Private Contact Discovery for Signal,” Signal (blog), September 26, https://signal.org/blog/private-contact-discovery.

¹¹⁴ B. Chor, E. Kushilevitz, O. Goldreich, and M. Sudan, 1998, Private information retrieval, Journal of the ACM 45(6):965–981, https://doi.org/10.1145/293347.293350.

¹¹⁵ E. Kushilevitz and R. Ostrovsky, 1997, “Replication Is Not Needed: Single Database, Computationally-Private Information Retrieval,” Proceedings 38th Annual Symposium on Foundations of Computer Science, https://doi.org/10.1109/sfcs.1997.646125.

¹¹⁶ R. Ostrovsky and W.E. Skeith, 2007, “A Survey of Single-Database Private Information Retrieval: Techniques and Applications,” pp. 393–411 in Public Key Cryptography—PKC 2007, https://doi.org/10.1007/978-3-540-71677-8_26.

¹¹⁷ H. Corrigan-Gibbs and D. Kogan, 2020, “Private Information Retrieval with Sublinear Online Time,” pp. 44–75 in Advances in Cryptology—EUROCRYPT 2020, https://doi.org/10.1007/978-3-030-45721-1_3.

¹¹⁸ E. Shi, W. Aqeel, B. Chandrasekaran, and B. Maggs, 2021, “Puncturable Pseudorandom Sets and Private Information Retrieval with Near-Optimal Online Bandwidth and Time,” pp. 641–669 in Advances in Cryptology—CRYPTO 2021, https://doi.org/10.1007/978-3-030-84259-8_22.

¹¹⁹ S. Garg, C. Gentry, S. Halevi, M. Raykova, A. Sahai, and B. Waters, 2016, Candidate indistinguishability obfuscation and functional encryption for all circuits, SIAM Journal on Computing 45(3):882–929, https://doi.org/10.1137/14095772x.

implementations that have been deployed—called “white box” cryptography—lack mathematical foundations for security, and typically get broken rapidly.

Another market need is for secure computation at speeds competitive with conventional microprocessors. The products that have been built to meet this need include specialized modes such as Intel’s software guard extensions (SGX) in general-purpose processors, as well as specialized tamper-resistant microprocessors such as those found in smart cards and mobile phones. As discussed in the Systems section of Chapter 4, these products can be broken if there are imperfections in the tamper resistance or bugs in the underlying implementations.

Quantum Key Distribution

Quantum key distribution (QKD) aims to establish secret keys for communications using quantum mechanical properties of photons, rather than the mathematical problems used in public-key cryptography. The practical applicability of the approach is limited to scenarios where senders and receivers directly exchange photons, such as over a private fiber connection.¹²⁰ As a result, QKD cannot be used on typical packet switched networks (such as the Internet), radio connections (such as Wi-Fi or mobile phones), or copper wire (Ethernet). As QKD does not provide any form of authentication, entities must authenticate each other by classical techniques such as prenegotiated secret keys or public-key technology. In addition, QKD trades a relatively well studied problem (implementing the mathematical operations involved in public-key cryptography) against less understood engineering problems associated with building secure optical equipment. Nevertheless, commercial systems have been offered for sale, and China operates an experimental satellite-based QKD system that has received much attention, including U.S. government plans for a competing system.

QKD may have niche applications in scenarios that require an extra layer of security against cryptanalytic attacks, and that can live within the limitations of its highly constrained quantum photonic channel. However, the fundamental limitations of QKD mean that, even with research or engineering advances, the approach will not play a significant role in the overall data security landscape.¹²¹

___________________

¹²⁰ See a recent survey, P. Sharma, A. Agrawal, V. Bhatia, S. Prakash, and A.K. Mishra, 2021, Quantum key distribution secured optical networks: A survey, IEEE Open Journal of the Communications Society 2:2049–2083, http://doi.org/10.1109/OJCOMS.2021.3106659.

¹²¹ NSA, 2021, “Quantum Computing and Post-Quantum Cryptography,” PP-21-1120, August, https://media.defense.gov/2021/Aug/04/2002821837/-1/-1/1/Quantum_FAQs_20210804.PDF.