Concrete Impacts of Abstract Geometry
You probably already know that mathematics has been around for thousands of years. You may also think that the era of discovery in mathematics is over and that mathematicians have proved all they can. The reality is just the opposite. New research in geometry and algebra is more active and groundbreaking than it’s ever been.
Having evolved in complexity for so many years, mathematics may seem mysterious, abstract, and disconnected from our modern world. But its impacts, emanating from modern and ancient discoveries, are far-reaching and profound. Here, we examine how abstract geometric concepts impact today’s technologies, including robotics, navigation, and quantum computing.
Centuries-Old Geometric Concepts
In the third century B.C.E., in the Greek city of Alexandria in North Africa, mathematician Euclid wrote a 13-volume book titled The Elements. In this foundational text, we find what is now called Euclidean geometry, which describes the relations between points, lines, and planes in two-dimensional and three-dimensional space. Fast-forward more than 2,000 years—Euclidean geometry is a part of today’s mathematics curriculum and is central to our understanding of all geometries. We now use the term Euclidean space when referring to the geometric system encountered in our physical world—or at least the physical world as we understood it before Albert Einstein uncovered its fundamentally non-Euclidean theory of relativity in the early 1900s. Understanding the geometry of Euclidean space has direct applications for surveying, construction, architecture, optics, and distance calculations.
Nearly two millennia after Euclid, René Descartes and Pierre de Fermat—both 17th-century mathematicians—independently identified a language for Euclidean space. They are credited with the observation that any location P in three-dimensional space can be described by three coordinates, x, y, and z. This algebraic language that describes Euclidean space—now known as the Cartesian coordinate system—forged a link between geometry and algebra that catalyzed research and discoveries for hundreds of years to come and is now standard in calculus, linear algebra, and differential equations.
The Evolution of Geometry
The evolution of geometry is natural and never-ending. Mathematicians strive to find new concepts based on old ones, and scientists are often looking for geometric structures and systems to model systems of interest.
Going beyond the typical three-dimensional Euclidean space, mathematics enables us to explore higher-dimensional spaces that account for complexity or an abundance of information. One option for exploring high-dimensional spaces is the language of feature vectors, which are used to describe different data properties and can vary widely in size. For example, a single color can be described by a three-feature vector that indicates the intensities of its red, green, and blue light components. A megapixel image consists of millions of these three-feature vectors and thus is best understood in a high-dimensional space.
In Euclidean geometry, a plane is composed of an infinite continuum of points—that is, a plane extends endlessly in all directions and has no gaps. But often space and movement are restricted—they are finite (or discrete and not continuous). For example, a chessboard is a discrete space because it’s an eight-by-eight grid. The movement of a chess piece also is discrete; if in play, a pawn must appear exactly on a white or black square and not a fraction between any two squares. In this way, a geometric representation of a chessboard is an eight-by-eight grid of points. On the other hand, the enormous (but finite) number of molecules in the atmosphere can best be understood via continuous geometry.
Objects of interest in Euclidean geometry include lines and planes. Not every object, however, is straight or flat—some objects are curved. While mapmakers do their best to depict Earth locally as two-dimensional, a two-dimensional plane cannot fully capture the nuances of a sphere-like surface. Fundamental, non-linear geometric objects—including circles, spheres, and cylinders—are spaces wherein the principles of Euclidean geometry do not hold.
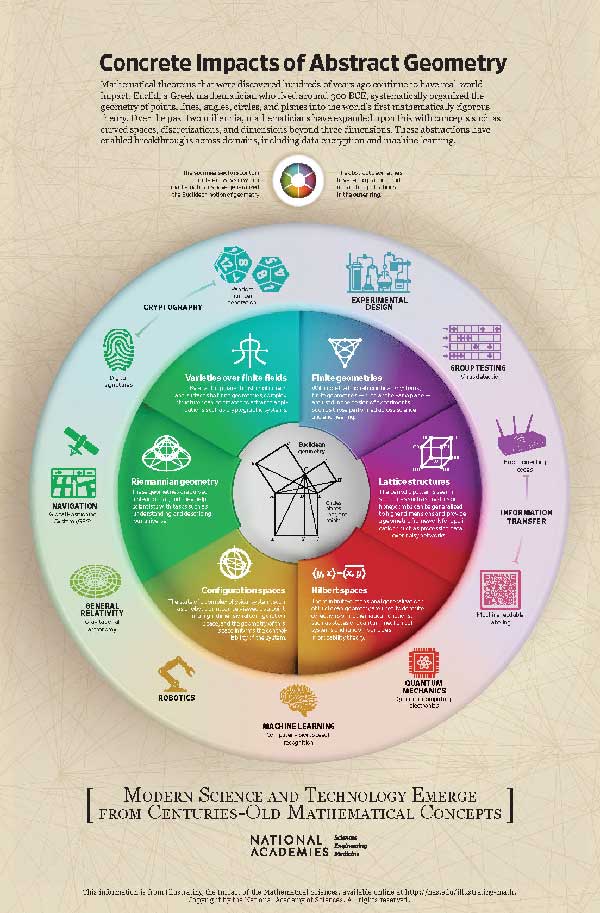
From the simple framework of Euclidean space and the Cartesian coordinate system, many key mathematical concepts—including Hilbert spaces, Riemannian geometry, finite geometries, lattice structures, varieties over finite fields, and configuration spaces—have evolved to address both abstract challenges and practical applications. Let’s explore some advancements in geometry and how they were created—or “abstracted,” as mathematicians would say—from Euclidean space and Cartesian coordinates.
Hilbert Spaces
Hilbert spaces are a key mathematical concept that has evolved out of Euclidean geometry. In these spaces, a point is an infinite sequence of numbers, yet familiar concepts like distances and angles can be measured. Hilbert spaces originated from the study of quantum mechanics, differential equations, and Fourier analysis.
Riemannian Geometry
Developed in the 1850s, Riemannian geometry is used to describe the geometry of curved spaces, known as Riemannian manifolds. In these spaces, notions such as straight lines, angles, distances, and areas deviate from the Euclidean concepts because the geometric structure varies from point to point. Some familiar examples of Riemannian manifolds, such as spheres, cylinders, and tori (plural of torus; “doughnut-shaped” surfaces), can be visualized—or “embedded,” as mathematicians would say—in ordinary three-dimensional Euclidean space. Other examples, such as the Klein bottle (see Figure 1) or the projective plane, cannot be easily visualized.
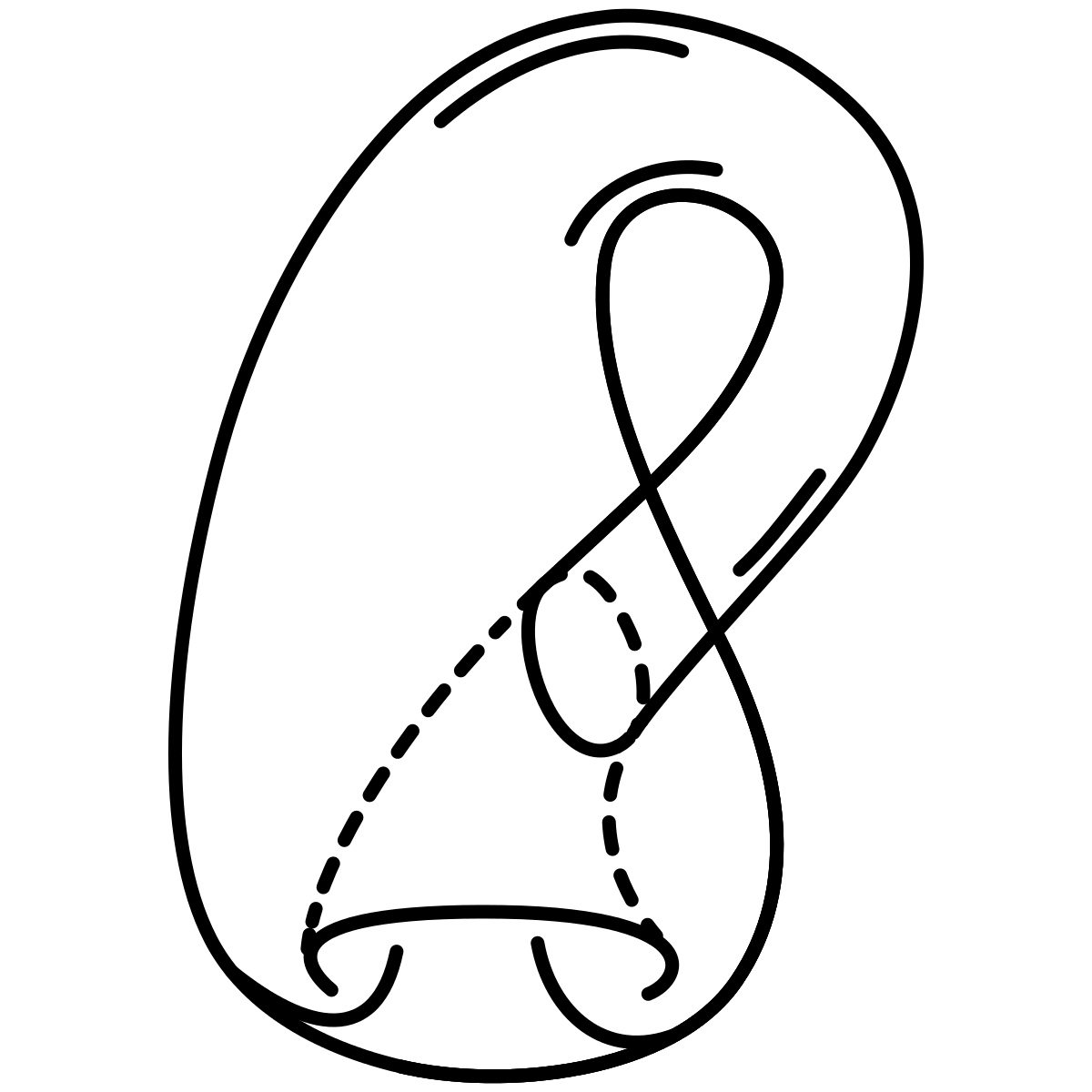
FIGURE 1 A Klein bottle representation. SOURCE: Yinweichen. 2015. “Klein Bottle.” https://commons.m.wikimedia.org/wiki/File:Klein_Bottle_Mark.svg. Licensed under CC BY-SA 4.0.
Finite Geometries
In Euclidean geometry, a line is composed of an infinite continuum of points. Starting in the mid-1800s, mathematicians studied systems called finite geometries, in which only a finite (or discrete) set of points is present. The Fano plane is a finite geometric space that is a highly symmetric configuration of seven points connected to each other by seven “lines” (see Figure 2).
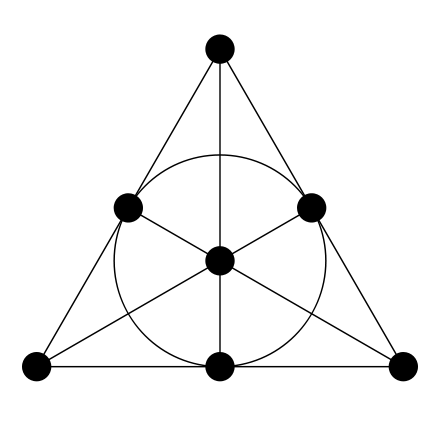
FIGURE 2 The Fano plane. SOURCE: Watchduck. 2021. “Fano Plane.” https://en.wikipedia.org/wiki/Fano_plane#/media/File:Fano_plane.svg. Licensed under CC0.
Lattice Structures
Digital data is often best represented in a high-dimensional discrete space, such as the Hamming cube (a geometric representation of the collection of all binary strings of 0s and 1s of a fixed length; see Figure 3) or a high-dimensional lattice. By lattice, we mean a periodically arranged collection of points that are evenly distributed in a Euclidean space. Real-world examples of such lattices include the locations of atoms in a crystal (which would form a three-dimensional lattice) or the vertices of a honeycomb (which would form a two-dimensional lattice). For digital data, we often consider more abstract, high-dimensional lattices consisting of points that are represented mathematically by a row of numbers (also known as a row vector).

FIGURE 3 A Hamming cube is used to represent high-dimensional data. SOURCE: Cburnett. 2006. https://en.wikipedia.org/wiki/Hamming_distance. Licensed under CC BY-SA 3.0.
Varieties over Finite Fields
It is possible to describe geometric spaces that are both finite and curved—for instance, by locating the solutions to a system of polynomial equations in modular arithmetic (where numbers restart when they reach a certain value, as is the case with a clock). These spaces, called varieties over finite fields, often have an extremely rich algebraic and number-theoretic structure. Prime examples of these are the elliptic curves over finite fields, which are connected to some of the most important problems in number theory.
Configuration Spaces
Configuration spaces are mathematical spaces, often of high dimension, that describe all the possible states (or “configurations”) of some system. For instance, to describe the position of 1,000 particles in a box, one might use a 3,000-dimensional configuration space, with a point in such a space being represented by 1,000 different (x, y, z) coordinates, each describing the location of one of these particles. To describe the position of a manipulator arm, we need to identify all the ways the manipulator can move. These degrees of freedom define the dimension of the configuration space of the manipulator. A position of the manipulator is a point in that space. The geometry of configuration spaces is complicated—in particular, it can require some serious mathematics to figure out an efficient and physically feasible way to transition from one configuration to another.
Geometry’s Impact
The impact of Euclidean geometry and its relatives is ubiquitous in modern science and technologies, even if the connection is not obvious—we often use innovations without necessarily understanding how or why they work. Here, several innovations in science and technology are identified, with insight into their geometric origins.
- Within quantum mechanics, the state of any quantum system is described using elements of a Hilbert space. This includes applications in quantum computing, condensed matter physics, and electronics.
- Riemannian manifolds are used to describe physically meaningful objects and are used extensively in computer vision and machine learning.
- Navigating the geometry of configuration spaces is necessary to control motion in robotics. Programming a robotic arm to move into a specific position requires correctly navigating the configuration space of that arm (i.e., the location of each joint of the arm).
- The nascent field of gravitational astronomy derives from the theory of general relativity and relies on an understanding of gravitational waves. These waves are fluctuations in the geometry of space and time that can be described only by using the abstract language of (pseudo-)Riemannian geometry.
- Navigation and astronomy have long relied on the mathematics of Riemannian geometries. More recently, accurately interpreting Global Positioning System (GPS) satellite data has required the use of Einstein’s theory of general relativity, which was developed using Riemannian geometry as a foundation. The unit quaternions, which are an example of a Riemannian manifold, can be used to describe all the ways a three-dimensional object can be rotated. Quaternions describe complicated maneuvers important for aerial navigation.
- Certain varieties over finite fields are widely used “under the hood” on the Internet today, because they are the most efficient way to set up a secure line of communication and to create digital signatures (an electronic way to sign messages and detect if unauthorized changes were made). They also play an important role in enabling random number generators and cryptographic systems.
- Finite geometries are often suitable models for science and technology. For example, combinatorial designs are often constructed from finite geometries and have many applications to tournament scheduling, error-correcting codes, and group testing.
- There are many different types of error-correcting codes, and some are constructed using carefully chosen high-dimensional lattices. As the name suggests, they allow data to be handled in a way that is resistant to noise, interference, or physical damage to the memory storage unit. Error-correcting codes enable QR codes (machine readable barcodes) as well as the transmission of image data from satellites.
These and many other modern scientific, technological, and engineering advances have emanated from centuries-old geometric concepts. While these concepts evolved from some straightforward ideas in Euclidean geometry, it is important to note that innovations in geometry are still happening. The evolution of research in geometry (and many other areas of mathematics) is not linear, and the advances that they will instigate and enable are difficult to anticipate. However, it remains clear that abstract geometry has had, and will continue to have, concrete impact.