Mathematical Functions Power Artificial Intelligence

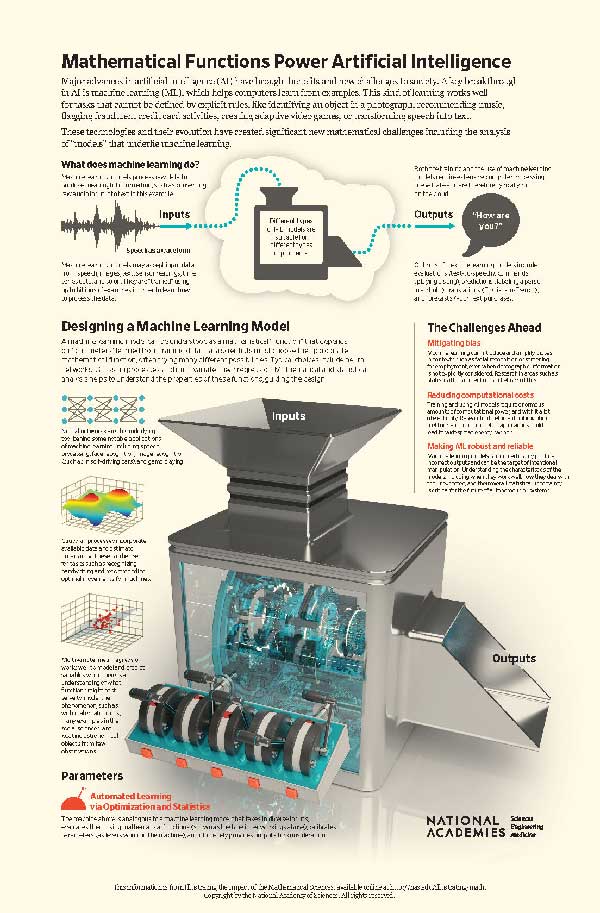
Mathematical Functions

Mathematical functions take an input (such as a number, a word, an image, or any other data that can be stored on a computer) and convert it to an output using a sequence of mathematical operations. We express this as f(x)=y, where f is the function, x is the input, and y is the output.

Consider the problem faced by the U.S. Postal Service of automatically sorting the mail. Part of this problem requires recognizing handwritten postal codes. We want a function f that takes an image (in its binary computer representation) as input, x, and outputs the correct zip code, y, as shown below in Figure 1.

And so on. There are many types of approaches—and many functions—to make this conversion from an image to something concrete like a number.

These mathematical functions can be relatively simple, using addition, multiplication, or logarithm. Many are more complex, involving a series of mathematical transformations. In machine learning, the learning part is determining the details of the mathematical transformations. For example, we might learn a function in the form f(x) = 5x + 2, where x is the input and 5x + 2 is the output, so that f(0) = 2,f(1) = 7,f(2)=12, and so on. This is simple arithmetic. The learning comes about in choosing the 5 and the 2 in the expression 5x+2, which are the parameters of the function. The general form of the function might be

f(x)= ax+b,

where the a and b represent the parameters to be learned. The choice of the general form of the mathematical function is very important, and where the expertise of data scientists is critical.

There are many possible choices for the mathematical function. The simplest is multivariate linear regression, where the output of the function is a weighted combination of the inputs. For example, a real estate agency might predict the sales prices of a home based on inputs such as the square footage, number of bedrooms, number of bathrooms, and so on. More recently, deep learning has enabled breakthroughs in domains such as image recognition and machine translation. Deep learning is usually described as an artificial neural network, but we can mathematically analyze deep learning as a nonlinear function that is itself a composite of alternating linear and nonlinear functions. A Gaussian process is a method for machine learning that includes uncertainty for the predicted outputs, which is useful in scenarios such as weather prediction. Mathematically, we can view the function being learned for Gaussian processes as a function that outputs other functions.

The qualities of the mathematical function determine its expressivity and complexity, and the mathematical field of functional analysis is needed to discern these traits.

Numerical Optimization

Whatever the function, numerical optimization is the mathematical method for learning the parameters. A parameter can be thought of as a variable that is internal to the model and that can be estimated from the data. Training examples, which are input-output pairs, are needed to learn the parameters of the function. Given a set of possible parameters, we evaluate the training examples to see how well the parameterized function predicts the desired output. Numerical optimization automatically adjusts the parameters to try to improve the predictions. The process can take many steps, like perfecting a recipe where you repeatedly bake cookies and have your friends taste them until everyone agrees they are perfect. Of course, in machine learning and life, there may never be perfect agreement!

Innovations in optimization, such as stochastic gradient descent, have enabled machine learning to handle the tsunami of data that has enabled the models to become much more powerful. Stochastic gradient descent uses a small subset of training examples at each iteration of the optimization—for example, having only 5 friends taste the cookies rather than 100. Not only does this make the optimization faster, but it can also help to find better parameters overall for reasons that are still a bit of a mathematical mystery.

Challenges

The massive growth in machine learning during the past decade has led to new challenges. These will not be solved by the mathematical sciences alone, but innovations in mathematics and statistics will be essential.

Mitigating Bias
Ideally, machine learning can mitigate biases and provide more objective predictions when used in areas such as medical diagnosis, screening for employment, and so on. As it is used today, however, machine learning may amplify biases in training data, even when biased features such as gender are not used. This depends in part on the choice of mathematical function. We need to devise and promulgate new methods and best practices in order to help people who deploy machine learning solutions do so in a way that does not exacerbate systemic biases.

Reducing Computational Costs
Current machine learning methods are extremely expensive to train and evaluate. A recent study found that training a single deep learning model requires an amount of energy comparable to the total lifetime carbon footprint of five cars. Approaches to speeding up the optimization in training of the models is an important area for development. Similarly, models can be extremely large and expensive to evaluate. This is why most phones cannot do text-to-speech directly but instead need to be connected to servers on the Internet. Newer developments in appropriate mathematical functions can help to address this.

Making Machine Learning Robust and Reliable
Despite its many successes, machine learning fails unpredictably and sometimes catastrophically. Efforts are needed to improve robustness and reliability, especially in situations where lives are at stake, such as with self-driving cars. This could include specific verification steps or other approaches. A major challenge in assessing uncertainty of machine learning models is the natural probabilistic nature of the problems. The training data, for example, represents only a sample of the overall data. The mathematical functions again play a role here because their properties can help to predict robustness and reliability.