The Mathematics of Internet Security
Communicating on the Internet is a bit like having a private conversation with a friend across a crowded room filled with people keen on hearing what you have to say. Lots of individuals (and organizations) have the opportunity to eavesdrop on or even manipulate messages you send and receive online. Yet, somehow, most of us communicate over the Internet without thinking about these risks. We use our credit card for online purchases, communicate with our doctor about our medical records, and access our bank accounts.
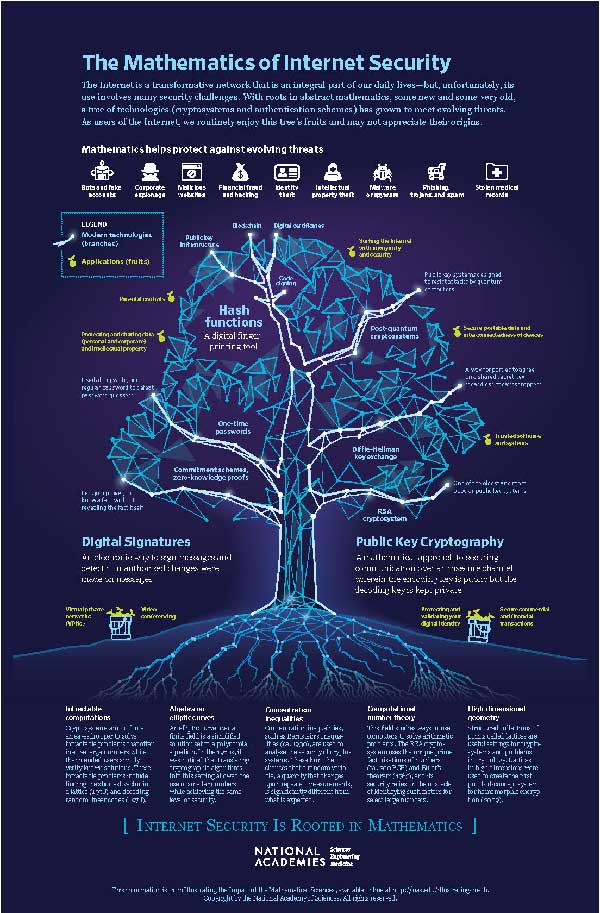
How is such privacy and security possible? Rooted in both new and very old mathematics, a tree of technologies (cryptosystems and authentication schemes) has grown and enables us to communicate from anywhere without fear of our data being manipulated, publicized, or used maliciously in other ways.
Broad Categories of Technology for Security
Public key cryptography is a critical technology for Internet security. Developed in the 1970s, it lets you send a message to a distant party that only they can read, without ever having to communicate in private. Essentially, the distant party can advertise to everyone, “here is how you can encode a message so that only I can read it,” and then you follow their instructions to send them an encrypted message. This is different from the way secret codes worked before, using symmetric cryptography, where the sender and recipient had to first communicate securely in private so that they could agree on the precise way to encode messages. A set of rules for encoding and decoding messages is called a cryptosystem. The security of a cryptosystem relies on the difficulty of quickly performing certain mathematical calculations. One of the most widely used methods for public key cryptography today, Rivest-Shamir-Adleman (RSA), often uses select numbers with more than 615 digits. It is currently intractable to factor such numbers into products of primes, which is what would be needed to break into the system. Diffie-Hellman is another popular method; it relies on the difficulty of calculating a so-called discrete logarithm. (A discrete logarithm is an analog of the logarithms we learned in school, but translated into a setting where the computation is not only more difficult but also currently intractable.) A popular version of this, Elliptic Curve Diffie-Hellman (ECDH), works with points on a mathematical object called an elliptic curve, where the points have coordinates with about 115 digits. Exploiting special properties of elliptic curves, ECDH gives a similar level of security as RSA while being more efficient by using smaller numbers. Another critical technology comes in the form of digital signatures. Instead of broadcasting how to encode an encrypted message to the sender, in this application the distant party broadcasts how to decode an encrypted message and check that it is really from them. The recipient can follow the instructions sent with an encoded message that purports to be from the sender, and if the digital signature is verified, they will know that the message has not been tampered with and is indeed from the sender. One common example is the Elliptic Curve Digital Signature Algorithm (ECDSA), which again exploits special properties of elliptic curves to provide security while using relatively small numbers. Hash functions, such as the Secure Hash Algorithm 3 (SHA-3), are a third critical set of tools that are used in many and surprising ways. These are rules that take a number or a message or a movie and produce a short “digital fingerprint” (hash) of that thing. Anyone who has one of these objects can calculate its fingerprint. Yet, given a fingerprint, it is intractable to find a message with that fingerprint, or even any two messages whose fingerprints agree. These functions appear “under the hood” of many technologies. In particular, they are used to provide a measure of anonymity to Bitcoin transactions and to provide protection to password storage; instead of storing passwords directly, most logon processes store the hash values of passwords. To test their security, the use of hash functions has been subjected to extensive attacks and analysis over the years. These analyses can be surprisingly abstract—often relying on advanced mathematical and computational methods—and are regularly needed to address new security challenges.Internet Security Is Rooted in Mathematics
These technologies help to establish Internet security, and all rely in a fundamental way on mathematics, some of which is very old. For example, RSA relies on Euler's theorem, which is more than 250 years old! It is astounding—but not unusual—that a piece of mathematics from 1763 can have its broadest and most impactful application today. As new mathematics is discovered every day, it builds upon existing mathematics and expands upon what is already known. Unlike technology, new mathematics does not replace old mathematics—the old mathematics remains true.
In addition, while new technologies are often built using mathematics, the demand for new technologies also stimulates the development of new mathematics.
Since around 2010, excitement over cryptocurrencies and related blockchains has exploded. Blockchains are a kind of tamper-proof public distributed database of digital information (blocks), typically consisting of records of transactions. People are excited to discover or invent new things to be done with blockchains and to find new and more efficient ways to engineer them. This has stimulated new applications of mathematics.
As one example, researchers used to study zero-knowledge proofs as an abstract topic with seemingly distant potential practical applications. These proofs provide a way for you to prove to someone else that you know a specific thing (such as an account number), without giving them any useful information about the thing itself (that’s why they are called “zero-knowledge”). This concept is subtle, and the whole subject used to be of largely academic interest, but now research in this area has become truly practical: zero-knowledge proofs are being put to real use as parts of some blockchains.
Internet security in an era of quantum computing is also motivating new mathematics. Quantum computers use the laws of quantum mechanics to process information and have the potential to solve certain computational problems faster than classical computers. In 1994, Peter Shor discovered a way that a quantum computer (if one existed) could break the encryption algorithms used in public key technologies. Today, it appears more and more possible that scientists will succeed in building a quantum computer that is powerful enough to render these technologies obsolete. Consequently, a global effort is under way to find strong and efficient post-quantum cryptosystems: replacements for RSA and the other vulnerable public key technologies. Such a new technology has to be based on the difficulty of solving a fundamentally different mathematical problem, something different from factoring whole numbers or finding discrete logarithms. Some of the hard problems being used in the design of cryptosystems include decoding random linear codes, finding an isogeny between given elliptic curves, and finding the short vector in a lattice.
Threats to safe use of the Internet will undoubtedly evolve, but mathematics will continue to support and enable new security technologies. Today, the combination of new and old mathematics allows us to feel confident that we are indeed communicating with the secure website that we think we are. It lets us do our banking online without fear that someone will eavesdrop and steal all of our money. And it lets us download apps on our cell phone without fear that some adversary will replace them with malware in route. While it is unclear what challenges to Internet security will emerge in years to come, we can be sure that many solutions will be rooted in mathematics.