Manufacturing with Mathematics
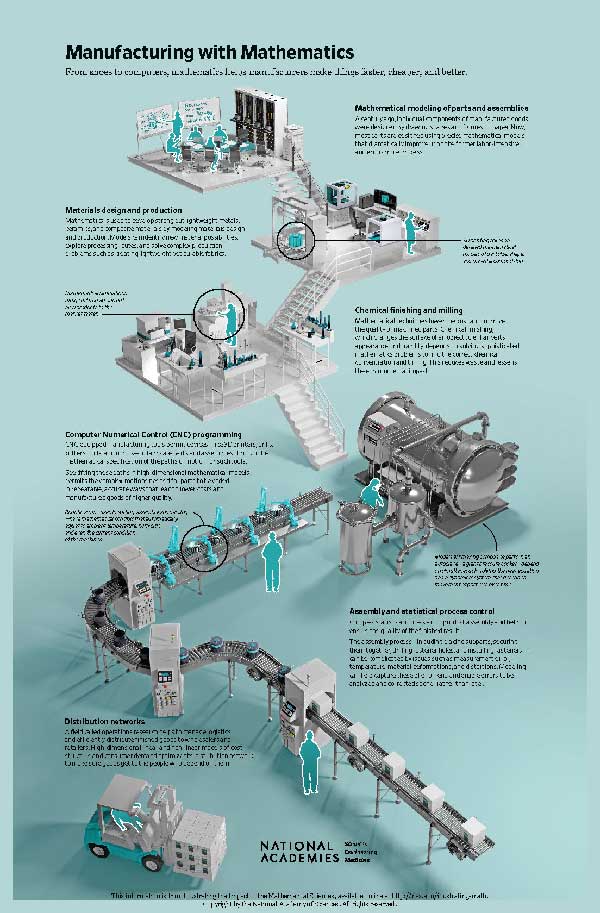
Mathematics and statistics are integral to the entire manufacturing process, from initial conception and design of a product, to production and finishing of parts, to assembly and distribution. The strategic deployment of mathematical techniques improves the efficiency and quality of goods for individuals, communities, and industrial sectors.
Mathematical Modeling of Parts and Assemblies
The manufacturing process begins with a product design. Fifty years ago, parts were designed by drawing curves, surfaces, and solids on paper or transparent film. Today, most parts are designed using computer-aided design tools that enable engineers to introduce and evaluate multiple design options entirely on computers. Given choices for materials and part designs, mathematical models can readily calculate strength, stresses, weight, material behaviors, manufacturability, and other key attributes and explore possible designs. This design approach can reduce uncertainty about how well the part will work, enhance quality, and reduce costs. The mathematical field of optimal design (also known as topology optimization) takes this even further and uses mathematical modeling to design complex configurations that may not be obvious otherwise.
Materials Design and Production
Mathematical models are often used to design materials and improve their manufacturability. These models can predict the resulting properties of materials—such as their expected strength, stiffness, or conductivity—and shed light on potential issues that may emerge at various physical scales. As just one example, mathematics can help determine optimal cure times and parameters (such as necessary pressure and temperature) for composite parts in an autoclave by utilizing computational fluid dynamics-based models to describe the internal chemical reaction that occurs.
Manufacturing Process Simulation
Mathematics and statistics are used to inform the manufacturing process. For conventional manufacturing processes and materials, we have centuries of knowledge—based on strong foundations in physics and chemistry—for predicting the properties of machined parts. But with newer manufacturing processes, such as additive manufacturing (also known as three-dimensional, or 3D, printing), there are many new manufacturing choices that affect the structure and properties of the manufactured part. Statistical analyses can then compare these models with real-world data from additive manufacturing machines to guide further improvements in the process.
Often, a part has to be finished in some way to enhance its appearance or durability before it can be put to use. Mathematics can guide these processes to reduce waste, lessen the environmental impact, and improve quality. For example, chemical finishing—which changes the surface of an object—depends on solving sophisticated reaction diffusion problems to find the correct chemical concentration and timing.
Statistical process control then aids in assembling finished products, including placing subparts, securing them together, drilling fastener holes, and installing fasteners, while also accounting for variability and maintaining control of the assembly process. Factors such as measurement error, temperature, and other irregularities can complicate assembly, but modeling, analyzing, and correcting errors help to ensure the quality of the finished product.
Automated Manufacturing
Various stages of the manufacturing process are continually being automated to increase production speed as well as reduce variability and costs. Computerized numerical control methods and mathematical optimization help automate devices such as 3D printers, drills, and cutters to perform complex tasks. The kinematic models built into device controls and the mathematics of optimal control dictate the overall sequence of manufacturing operations and enable precise control of the process.
Distribution
Once products are complete, operations research methods determine the most efficient approach for packaging, routing, and distributing finished goods to retailers and individuals. Modeling all of the planning and scheduling decisions leads to high-dimensional nonlinear models of time and cost, which are difficult to solve without mathematical optimization algorithms. These tools help goods reach the people who depend on them.